轮式移动机器人的三维轨迹跟踪控制

李小凤，黄宜庆，袁梦茹（安徽工程大学电气工程学院，安徽芜湖 241000）



轮式移动机器人的三维轨迹跟踪控制

李小凤，黄宜庆＊，袁梦茹
（安徽工程大学电气工程学院，安徽芜湖 241000）

摘要：针对轮式移动机器人的轨迹跟踪问题，提出了一种基于自适应反演滑模技术的三维轨迹跟踪控制方法．首先，根据坐标变换理论，建立轮式移动机器人的动力学方程和位姿方程；其次，采用反演方法（Backstepping）设计切换函数，将反演控制方法与滑模控制方法相结合，设计一种自适应反演滑模控制器，实现了轮式移动机器人的三维轨迹跟踪控制；最后，数值仿真表明三维轨迹跟踪控制方法与传统的PID控制方法相比，具有更高的控制精度，同时在一定程度上削弱了传统滑模控制所固有的抖振．

关 键 词：轮式移动机器人；反演滑模控制；轨迹跟踪；抑制抖振

近年来，轮式移动机器人不仅在工业和服务业得到了广泛的关注，而且在控制理论方面，以轮式移动机器人为具体控制对象的研究已成为热点．轨迹跟踪是轮式移动机器人现阶段控制的主要问题之一．然而轮式移动机器人具有高度非线性和非完整性，从而使其轨迹跟踪控制具有很大挑战性．移动机器人轨迹跟踪控制方法大致分为鲁棒控制、智能控制、自适应控制、反演控制以及滑模控制等．Sharbafi［1］等采用智能控制方法，实现对移动机器人的运动轨迹跟踪控制．陈罡［2］等通过引用饱和函数和横截函数的思想，针对有界干扰的移动机器人提出了一种饱和自适应鲁棒控制方法．基于神经网络滑模控制的方法，付涛［3］等实现了对移动机器人的全局轨迹跟踪控制．根据非完整约束的轮式移动机器人的运动学模型，席雷平［4］等采用反演控制的相关理论和方法，设计了控制器，保证了系统的稳定性．吴忠伟［5］等基于模糊控制方法和Lyapunov理论，设计了一种具有模糊规则的滑模控制器．

滑模控制作为一种鲁棒性强、抗干扰性强的变结构控制方法，由于其具有响应快速、算法简单、对模型要求低等优点而被广泛运用于移动机器人的控制．反演控制的方法将复杂的非线性系统分解成不超过系统阶数的子系统，为每个子系统设计Lyapunov函数，有效地保证了系统的稳定性．常盛［6］等结合滑模控制和模糊控制的优势，提出了一种自适应模糊滑模控制器，很好地解决了系统的不确定性问题，但模糊模型归纳不够完善，且不能自学习．李文波［7］等采用神经网络补偿的方法，设计了一种快速光滑终端二阶滑模控制器，提高了控制的速度和精度，但该控制器不能很好地实现神经网络的实时在线更新．针对轮式移动机器人建模系统中存在的误差和外界干扰，杨兴明［8］等设计了一种基于反演技术的运动学控制器和滑模动力学控制器相结合的控制算法，有效地削弱了抖振，实现了全局渐进稳定的轨迹跟踪控制．上述对轮式移动机器人轨迹跟踪控制的研究中，所建立的模型大多数都集中在二维平面，这一约束难以满足移动机器人多目标控制的要求．考虑轮式移动机器人在三维螺旋面上的跟踪控制问题，提出一种基于反演滑模技术的轨迹跟踪控制方法．首先，假设轮子与地面间无打滑现象，建立了轮式移动机器人的运动学模型；采用反演技术设计滑模控制器的切换函数，通过设计的反演滑模控制器最终实现了轮式移动机器人的三维轨迹跟踪控制；最后，数值仿真实验说明了方法的有效性．

1 轮式移动机器人的动力学模型

以四轮轮式移动机器人为研究对象，其中，两个后轮为驱动轮，两个前轮为从动轮，左右两个后轮各由一个电机来驱动，如果两个电机的转速不同，则两个后轮会产生差动，从而可实现转弯．机器人在三维面上的位姿误差坐标如图1所示．在螺旋式盘旋公路上，轮式移动机器人的状态由其两个驱动轮的轴中点M在坐标系中的位置和航向θ来表示，机器人在螺旋公路上从M点经过时间t运动到N点，相应的坐标系由X －Y－H轴变换到Xe－Ye－He轴（H轴和He轴共轴），N′点为N点在X－Y平面上的投影．

令p＝（x y hθ）T，q＝（v w）T，其中，（x，y，h）为轮式移动机器人初始位置M点在坐标系X－Y－H轴中的位置，（xe，ye，he）为轮式移动机器人运动到N点在坐标系Xe－Ye－He轴中的位置，（xr，yr，hr）为轮式移动机器人运动到N点在坐标系X－Y－H轴中的位置．θ为移动机器人在X－Y平面（水平面）上的前进方向与X轴的夹角，θe为移动机器人运动到N点时的前进方向与Xe轴的夹角，θr为移动机器人运动到N点时的前进方向与X轴的夹角，即θr＝θ＋θe．β为给定螺旋面与水平面的夹角，v和w分别为轮式移动机器人的线速度和角速度，在动力学模型中它们分别是系统的控制输入．移动机器人的动力学方程［9］为：

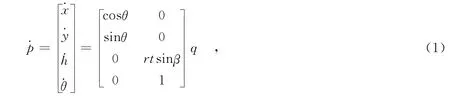
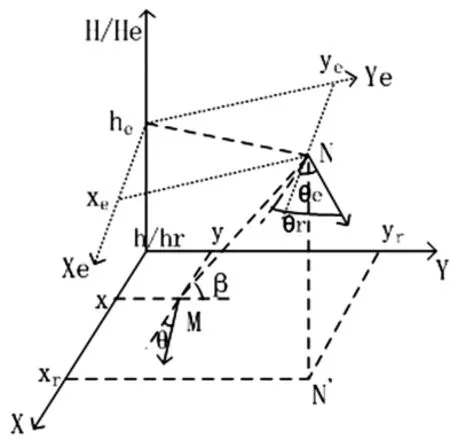
图1　机器人在三维面上的位姿误差坐标

设水平面上新坐标系Xe－Ye与坐标系X－Y之间的夹角为θ．根据坐标变换公式可得描述移动机器人位姿的误差方程为：

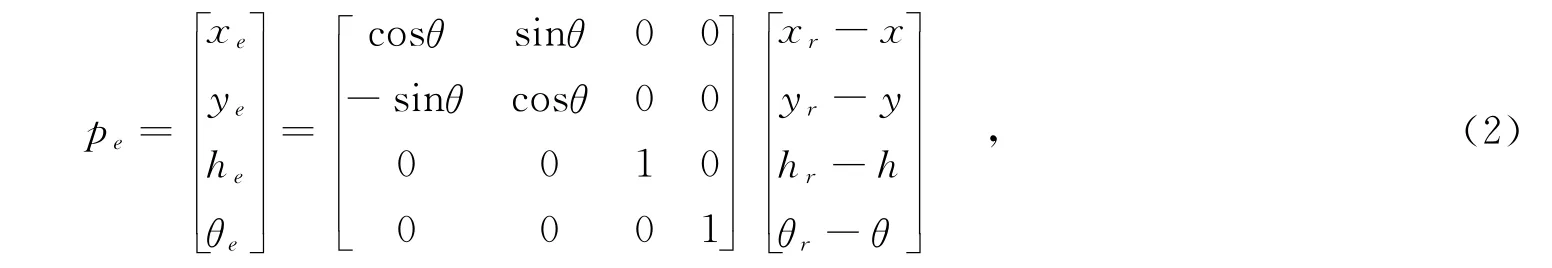
进一步可以得到位姿误差微分方程为：

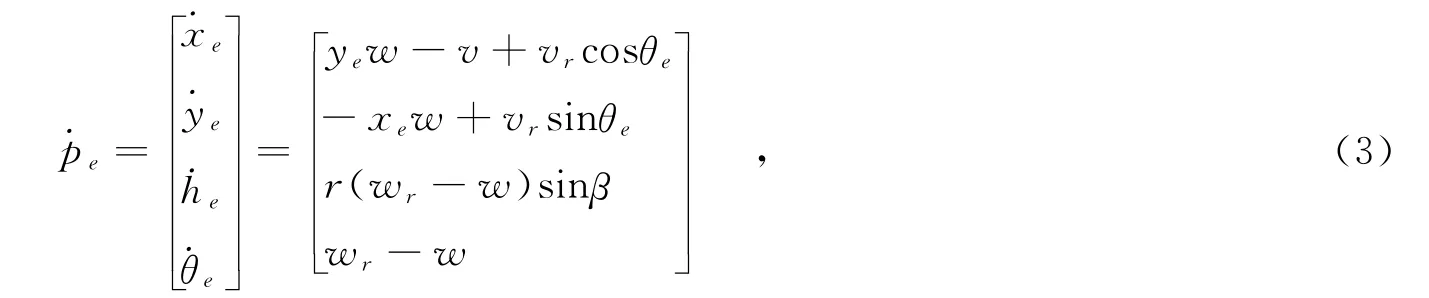
轮式移动机器人轨迹跟踪控制的目标是对任意的初始误差在输入q＝（v w）T的作用下，使θe）T有界，且

2 反演滑模控制器的设计

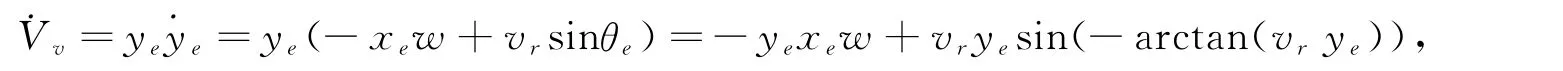
根据上述讨论的结果，设计如下形式的切换函数［10］：

当xe＝0时，选取如下形式的Lyapunov函数

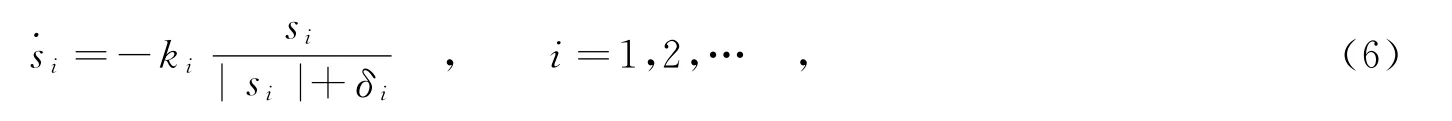
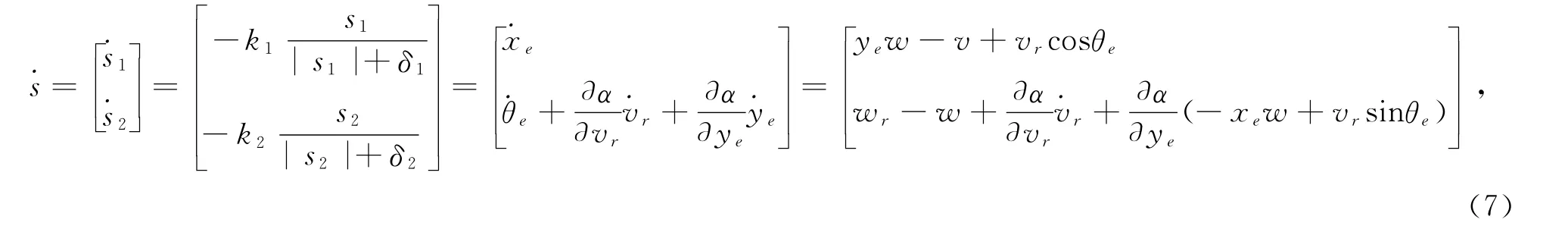
通过整理，得到相应的控制律为：

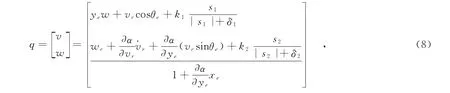
3 数值仿真

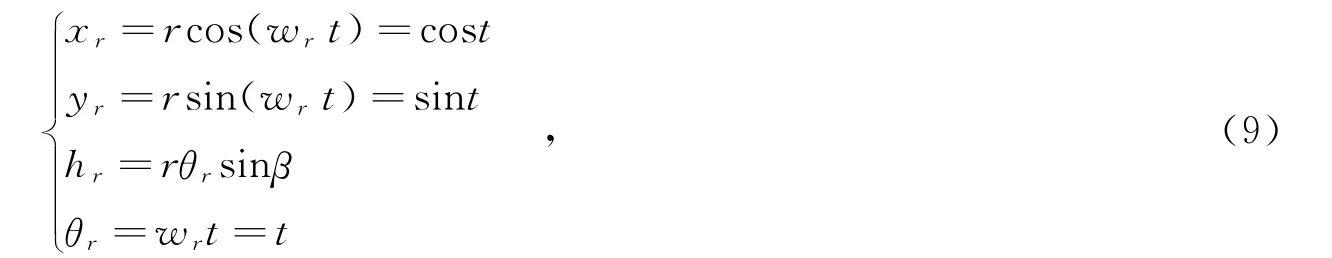
以轮式移动机器人为研究对象，假设跟踪线速度v和角速度w均为匀速运动，其运动轨迹在水平面上是圆轨迹，在垂直面上是直线轨迹．取，则，水平面圆的半径为1．0，位姿指令pr＝（xryrhrθr）T表述如下：选取控制器参数δ1＝δ2＝0．02，k1＝k2＝6．0，位姿误差初始值为［0 1 0 0］．同时，将三维轨迹跟踪控制方法与传统PID控制方法进行比较，仿真结果如图2～图7所示．其中，轮式移动机器人三维轨迹跟踪曲线如图2所示．由图2可知，在仿真初期由于外界的干扰，使得系统出现一定的波动，随着时间的推移，由于反演滑模控制器的作用，系统逐渐稳定．轮式移动机器人在x轴、y轴和h轴方向的轨迹跟踪误差如图3、图4、图5所示．由图3、图4、图5可知，三维轨迹跟踪控制方法在x轴和h轴方向的跟踪误差明显小于PID控制方法，控制精度更高．两种控制方法的控制器输出曲线分别如图6、图7所示．

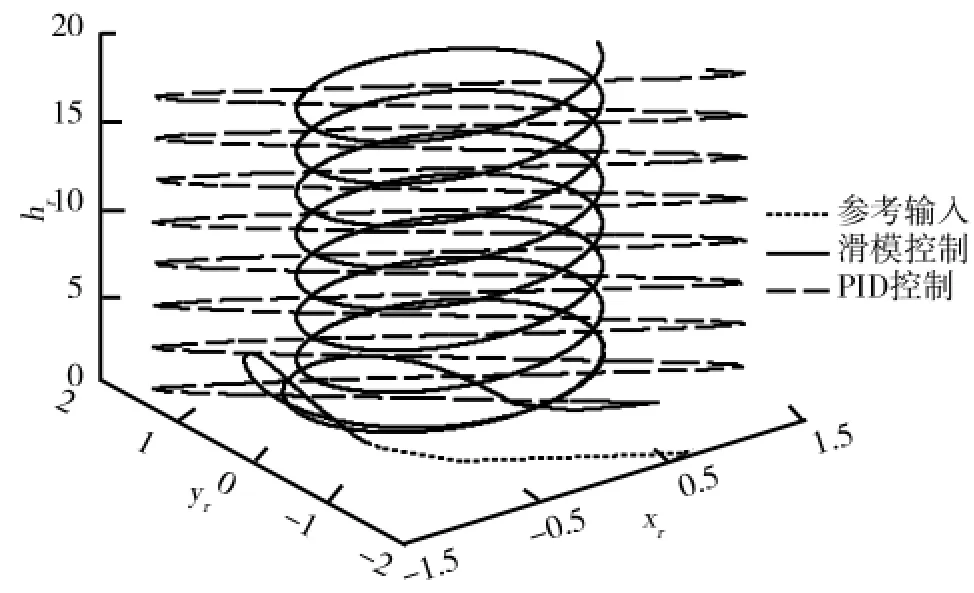
图2　三维轨迹跟踪曲线　

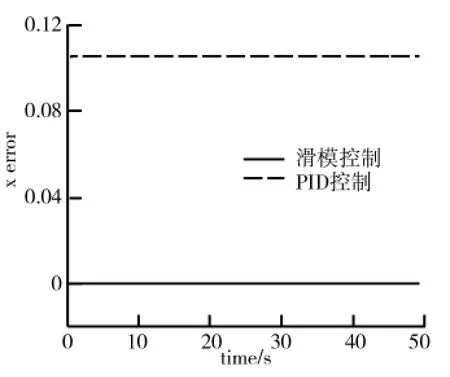
图3　x轴方向跟踪误差

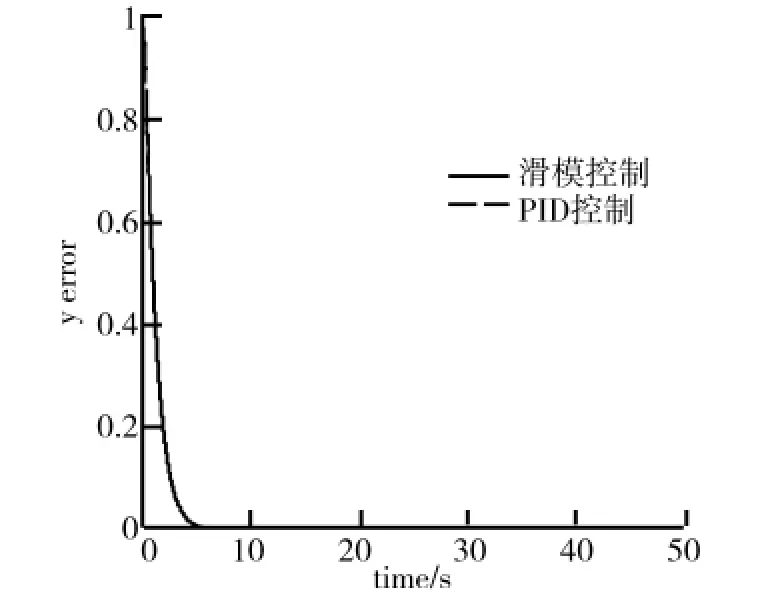
图4　Y轴方向误差　

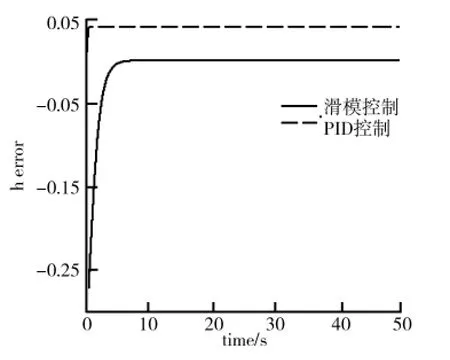
图5　H轴方向误差

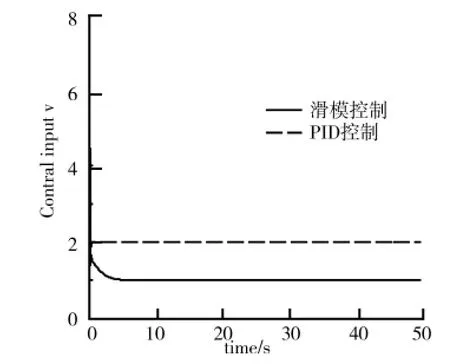
图6　控制输入信号v　

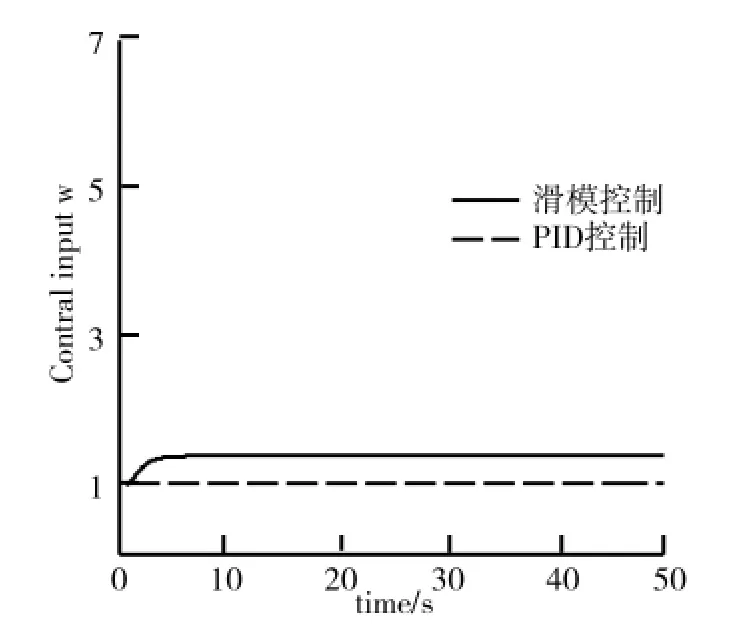
图7　控制输入信号w

4 结论

以轮式移动机器人为研究对象，提出了一种基于反演滑模技术的三维轨迹跟踪控制方法．在滑模控制器的设计过程中，采用反演技术设计切换函数，以保证稳定的滑动模态．同时，将提出的方法与传统的PID控制方法进行了仿真比较，仿真结果表明，反演滑模控制器具有更高的控制精度，减小了轮式移动机器人的轨迹跟踪误差，在一定程度上消弱了传统滑模控制所固有的抖振．

参考文献：

［1］ M A Sharbafi．Motion control of omni－directional three－wheel robots by brain－emotional－learning－based intelligent controller［J］．IEEE Transactions on Systems，2010，40（6）：630－638．

［2］ 陈罡，高婷婷，贾庆伟，等．带有未知参数和有界干扰的移动机器人轨迹跟踪控制［J］．控制理论与应用，2015，32（4）：491－496．

［3］ 付涛，王大镇，弓清忠，等．改进神经网络自适应滑模控制的机器人轨迹跟踪控制［J］．大连理工大学学报，2014，54（5）：523－531．

［4］ 席雷平，段连飞，江涛．非完整四轮式移动机器人反演轨迹跟踪控制［J］．计算机测量与控制，2012，20（8）：2 143－2 145．

［5］ 吴忠伟，尚小晶．轮式移动机器人轨迹跟踪控制方法［J］．长春大学学报，2014，24（2）：146－150．

［6］ 常盛，王福明．车辆主动悬架自适应模糊滑模控制研究［J］．机械工程与自动化，2014（2）：144－147．

［7］ 李文波，王耀南．基于神经网络补偿的机器人滑模变结构控制［J］．计算机工程与应用，2013，50（3）：251－255．

［8］ 杨兴明，朱建，高银平，等．欠驱动移动机器人的路劲跟踪控制［J］．合肥工业大学学报，2014，37（1）：53－58．

［9］ 宋占峰．道路线路实时动态三维可视化设计理论和方法的研究［D］．长沙：中南大学，2003．

［10］G Bartolini，A Piasno，E Punta，et al．A Survey of applications of second－order sliding mode control to mechanical systems［J］．International Journal of Control，2003，76（9）：875－892．

Three－dimensional trajectory tracking control for wheeled mobile robot

LI Xiao－feng，HUANG Yi－qing＊，YUAN Meng－ru
（College of Electrical Engineering，Anhui Polytechnic University，Wuhu 241000，China）

Abstract：A robust three－dimensional trajectory tracking control strategy for wheeled mobile robot via adaptive backstepping sliding mode technique is presented．Firstly，the wheeled mobile robot dynamics equation and position equation are obtained by coordinate transformation theory．Then，switching function is designed by backstepping method and an adaptive backstepping sliding mode trajectory tracking controller is developed for the wheeled mobile robot system．Finally，compared with PID control method，simulation results show that the proposed method has higher control precision and reduces chattering existing in conventional sliding mode control．

Key words：wheeled mobile robot；backstepping sliding mode control；three－dimensional trajectory；tracking control

通讯作者：黄宜庆（1983－），男，安徽芜湖人，讲师，博士．

作者简介：李小凤（1991－），女，湖北荆门人，硕士研究生．

基金项目：国家自然科学基金资助项目（61304127）

收稿日期：2016－01－10

文章编号：1672－2477（2016）01－0048－05

中图分类号：TP242．6

文献标识码：A