基于数学形态学滤波的电压暂降检测方法

康军胜，刘桂英，廖耀华，李 琳，范 丰（长沙理工大学电气与信息工程学院，湖南长沙410114）



基于数学形态学滤波的电压暂降检测方法

康军胜，刘桂英，廖耀华，李 琳，范 丰
（长沙理工大学电气与信息工程学院，湖南长沙410114）

摘要：针对动态电压恢复器对电压暂降特征量检测的实时性和准确性要求，与移相小角度的αβ－dq变换相结合，提出了一种使用双结构数学形态学滤波的快速电压暂降检测方法。即将构造出的双结构数学形态学滤波器对电网单相电压中的谐波、噪声等干扰进行预处理后，将待测单相电压移相一个小角度形成相互垂直且正交的αβ两相电压，再采用αβ－dq变换并用数学形态学滤波器代替传统的二阶巴特沃斯低通滤波器实现对非直流量的滤波，实现实时、准确地检测电压暂降发生的起止时间、暂降幅值和相角变化；为避免锁相过程产生的延时和输出误差，用基波特征参考值代替锁相环节；该方法原理清晰、计算简单。仿真实验结果表明该方法具有抗干扰、延时小、检测结果准确性高的优点。

关键词：电压暂降；形态学滤波；移相小角度；αβ－dq变换；仿真

0 引言

随着精密用电设备的广泛使用及其对电能质量的要求不断提高［1］，电能质量扰动对用户的影响也日益增大。动态电压恢复器（Dynamic Volt⁃age Restorer，DVR）是一种可靠保证敏感负荷的供电电压在受到系统电压扰动时仍处于安全工作范围的串联型补偿装置。实现电压暂降的分析和检测，对于研究相应的预防和保护措施具有重要的意义［2］，也是实现电压暂降动态补偿的关键。

由于配网系统中电网电压暂降大多由电网单相故障引起，实现对单相电压暂降的检测并实施有效治理措施己引起了国内外的广泛关注［3］。单相系统中需要构造出虚拟的三相系统，才能运用d⁃q变换。单相系统构造出相互垂直且正交的两相电压，才能通过αβ⁃dq变换进行检测。

文献［4］利用单相电压延迟60°构造虚拟的三相系统和文献［5］根据实测的单相电压延时90°来构造静止坐标系中的α、β分量是两种用移相构造对单相电压暂降进行检测的方法，该方法检测实时性差。虽然文献［6］利用求导的方法将单相电压由αβ静止坐标系转换到d⁃q旋转坐标系，使得检测计算量减少，但仍没有克服求导法本身的缺陷；文献［7］提出的改进算法是在αβ⁃dq变换检测法的基础上，利用单相电压移相一个可调的角度构造出相互垂直且正交的两相电压。该方法虽然计算简单，但由于使用锁相环（PLL）和电网中谐波、噪声等干扰的存在，使用传统的巴特沃斯低通滤波器已满足不了动态电压恢复器中对电压暂降检测的实时性和准确性要求。

本文根据数学形态学滤波和移相小角度电压暂降检测方法的基础上，提出了一种使用双结构数学形态学滤波的快速电压暂降检测方法。即利用构造出的双结构数学形态学滤波器具有的良好非线性低通滤波特性，对电网单相电压中的谐波、噪声等干扰进行预处理后，将待测单相电压进行移相小角度的αβ⁃dq变换并用数学形态学滤波器代替传统的二阶巴特沃斯低通滤波器实现对非直流量的滤波，实现实时、准确地检测出电压暂降发生的起止时间、暂降幅值和相角变化。所用到的基波特征参考值实时得到，取代了锁相环节。该方法原理清晰、计算简单，避免了传统检测方法的缺点。仿真结果表明该方法具有抗干扰能力强、检测延时小、检测结果准确性高的特点。

1 延时小角度电压暂降检测方法

由单相电压通过移相来构造αβ坐标系中的uα、uβ分量，具体过程如下：如图1所示，令待测量u1等于矢量uβ即uβ＝u1＝Usin（ωt＋δ），uδ由uβ移相角度δ得到；uδ幅值同样为U；由uδ端点向uα作垂线交uα反向延长线于一点，得到与uβ方向相反的矢量u01和与uα方向相反的矢量u02。

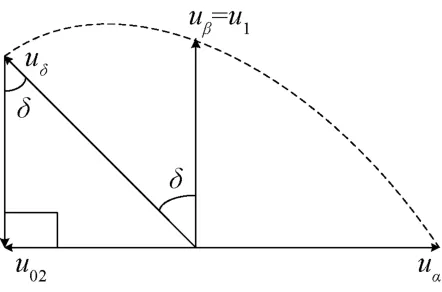
图1　移相角度δ构造αβ量矢量图

显然矢量u01的幅值为Ucosδ，即：u01＝－uβcosδ。

矢量u02的幅值为Usinδ，即：u02＝－uαUsinδ。

又可知，矢量u02＝u01＋uδ，即

－uαsinδ＝uδ－u01cosδ

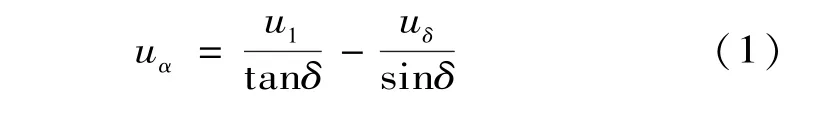
化简得到式中：δ为可移相的角度。

图2中uα＝Ucos（ωt＋δ）和uβ＝Usin（ωt ＋δ）分别为电压矢量在αβ静止坐标系两个坐标轴上的投影。由原理知电压矢量与d⁃q旋转坐标系同步旋转，d⁃q旋转坐标系相对于静止坐标系以角速度ω旋转。其中ud＝Ucosδ和uq＝Usinδ由电压矢量在d⁃q旋转坐标系的投影得到。由以上分析可知uα和uβ变换到d⁃q坐标系的算法如下：

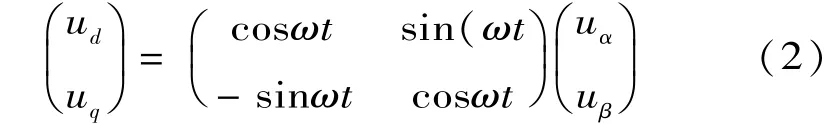
假设每个工频周期采样点数为N，移相角δ可以选取为360 k／N（k为正整数）。uδ由当前采样点之前的第k点得到。当k很小时，检测结果与用差分求导法的检测结果近似等效。

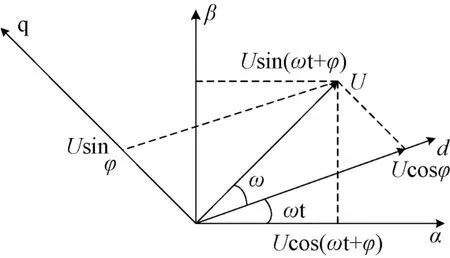
图2　αβ坐标系变换d⁃q坐标系

将式（1）代入式（2）进一步推导，可得

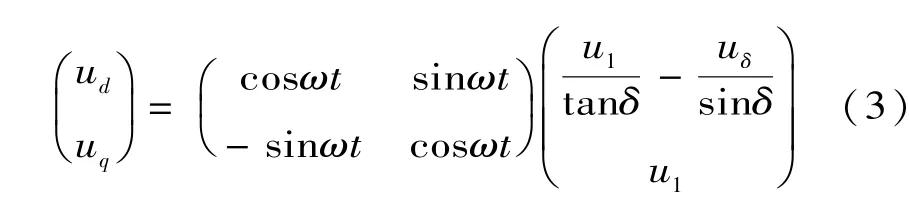
当信号中含有谐波时，设

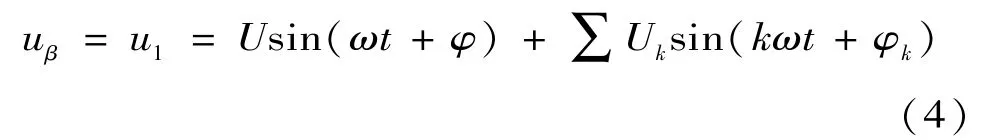
则

将式（4）、式（5）代入式（3），运算可得

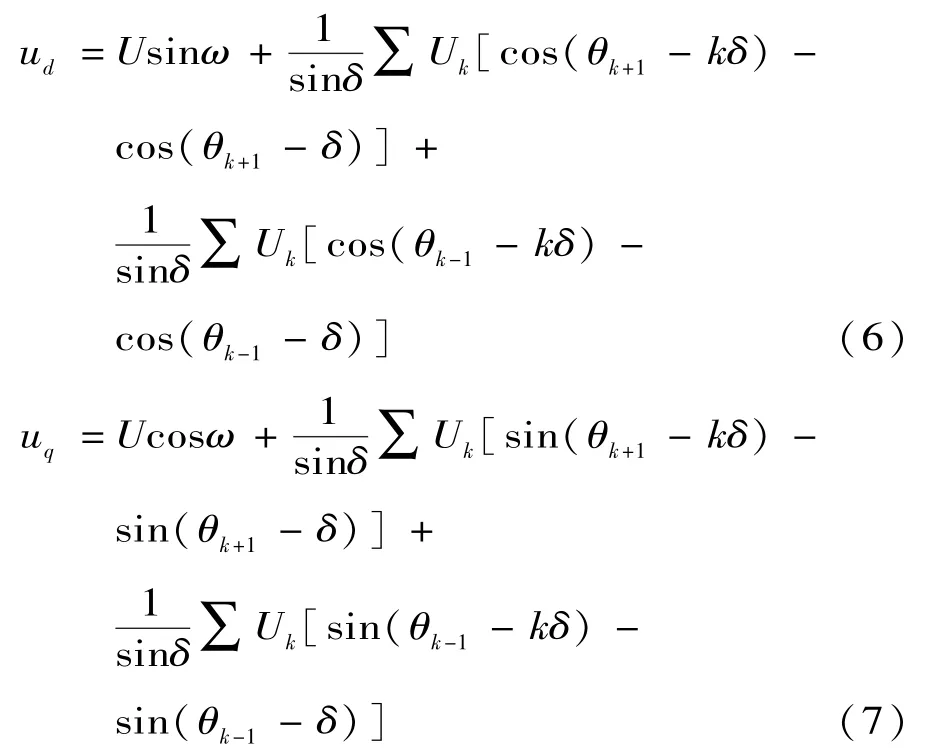
式中：θk＋1＝（k＋1）ωt＋φk，θk－1＝（k－1）ωt＋φk。用低通滤波器进行滤波可得到直流分量ud0和uq0，则基波电压的幅值和相位跳变分别为

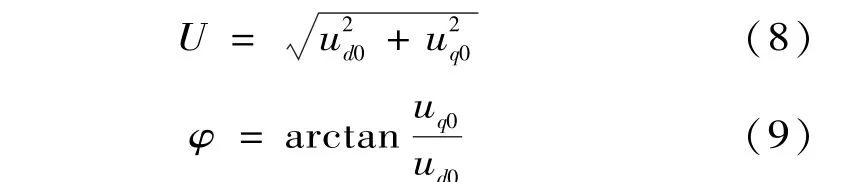
由式（6）、式（7）可知，电压基波在运算结果中表现为直流分量，第k次高频振荡信号被分解成k±1次高频振荡信号的叠加。

综上分析及文献［7］的仿真结果可知，当移相角δ较小时，检测延时小，对信号中的扰动分量有较大的放大作用；当移相角δ较大时，减小对扰动的放大作用，检测延时随之增大［7］。为增加抗干扰能力、减小检测延时、提高检测精确性，需要新型的滤波器与该方法配合使用。

2 新型数学形态学滤波的实现

2. 1 数学形态学滤波的基本原理

数学形态学滤波是在数学形态学［8］的基础上，利用预先设定好的结构元素对信号进行形态学处理和分析来提取出有用信息，以达到噪声抑制的目的。与传统的低通滤波器相比，主要是由布尔运算和少量加法运算组成的形态学滤波器具有运算简单且延时短的优点［9］。利用腐蚀来定义开运算、膨胀来定义闭运算。

设采样一维多值信号得到输入序列f（n），定义域为D（f）＝｛0，1，2，…，N－1｝，预设的一维结构元素序列为g（x），定义域为D（g）＝｛0，1，2，…，M－1｝；其中M和N为N≥M的整数。则膨胀和腐蚀运算分别定义为

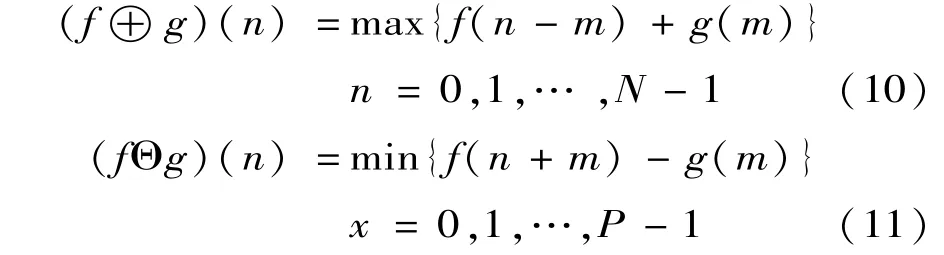
式中：⊕为膨胀运算；Θ为腐蚀运算。

由式（10）和式（11）可得到形态学开、闭运算定义分别为

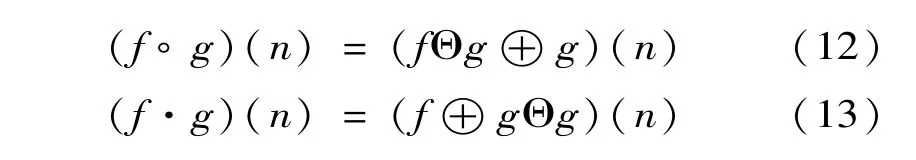
式中：ೲ为开运算；·为闭运算。

基于开、闭运算可以构建以下3种滤波算法：交替滤波器

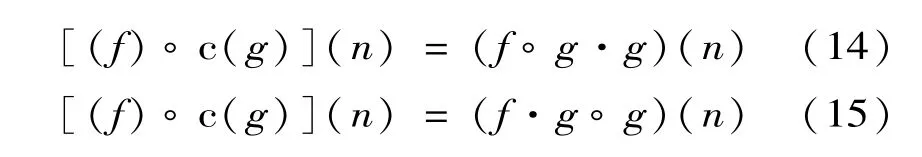
混合滤波器

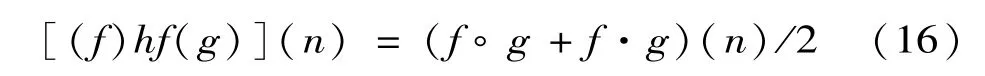
交替混合滤波器

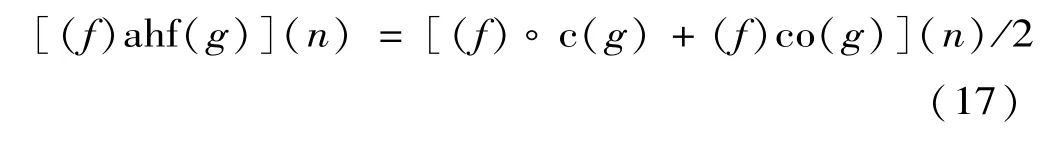
2. 2 构造双结构数学形态学滤波器

形态学滤波器的滤波效果不仅依赖于滤波器的变换形式、结构元素的形状和长度，为有效滤波还需结构元素的形状、长度匹配所要滤除的信号。其中结构元素形状的选取最为关键。

常用结构元素的形状有余弦、半圆、三角、直线等［10］。文献［11］根据电力系统数据采集中常见的噪声干扰，将几种常用结构元素的滤波特性进行了详细的仿真对比。余弦结构元素具有滤波效果好、运算速度快的优势，在处理高频连续干扰、随机背景噪声时，可优先考虑使用。半圆结构在处理脉冲噪声干扰时不仅在滤波上有很好效果，也有较快的计算速度。直线结构元素对直流偏移量干扰，有提取作用。由于电网电压中多样性的噪声干扰和对滤波速度的要求，为更好的发挥各结构元素的滤波优势，本文采用余弦型结构和半圆型结构的双结构元素组成的交替混合滤波器。其基本形式如图3所示。

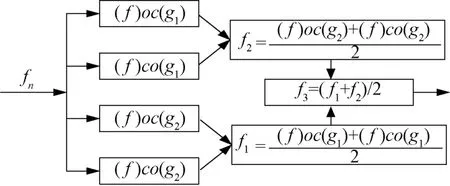
图3　双结构交替混合滤波器

其中，g1表示为余弦结构元素；g2表示为半圆结构元素；输入信号通过交替混合滤波器的输出分别为f1、f2。

2. 3 基波特征参考值的计算方法

根据文献［9］中原理，可将实时得到的基波特征参考值取代传统方法中的锁相环，避免输出误差和锁相延时。为此正确得到式（3）中的sinωt和cosωt极为关键。电压暂降会引起系统电压的畸变，采用如图4所示方法可得到稳定正弦正交的参考值［12］。

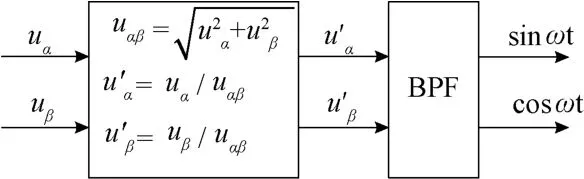
图4　基波特征参考值的形成

单相电压变换后得到正交电压uα和uβ。由于电压发生暂降时，uα不再正交于uβ，经过图4的变换后，可得到正交的参考电压。由于得到不一定为正弦量的u’α和u’β，故需要通过带通滤波器才能得到相应的基波特征参考值，即sinωt和－cosωt。

2. 4 新型电压暂降检测方法

基于数学形态学滤波的电压暂降检测方法的实现可用流程图如图5所示。

图5　新检测方法流程图

u0为实测的电网单相电压矢量，使用本文提出的双结构形态学滤波器对实测的单相电压中所含有多种形式的噪声干扰和谐波进行滤波预处理。经移相小角度的αβ⁃dq变换后所获得的直流分量中仍会含有少量的噪声干扰。直线型结构元素的特点是可以滤除直流分量中的各次谐波，滤波精确度高，实时性好［13］。此时选用单结构元素的直线型形态滤波器代替二阶巴特沃斯低通滤波器进行低通滤波，从而快速、精确的得到电压暂降的三个特征量。

3 系统仿真分析

利用Matlab／Simulink仿真软件对单相电压发生的电压暂降事件进行仿真比较分析，发生暂降的相电压幅值为220 V、基波频率为50 Hz。

DVR装置主电路拓扑结构为公用直流母线的三单相桥结构［14］，各相可独立进行补偿，互不影响；逆变器直流侧储能装置为电容器。本文提出的单相检测方法可很好应用于上述结构。

设定在时间0. 087～0. 163 s幅值暂降50%，0. 16 s相位跳变30°，含有的谐波情况与文献［7］中相同，即幅值为12 V、10 V、9 V、8 V的5、7、11、13次谐波，并有白噪声和脉冲噪声干扰。加入功率为0. 02 dBW的白噪声干扰，在0. 088 s和0. 164 s加入幅值为110 V的脉冲噪声干扰。

3. 1 单相电压原始波形预处理

仿真对比中，电压采样频率为10 kHz，二阶巴特沃斯低通滤波器的截止频率180 Hz，就滤波效果、运算速度的比较衡量来进行结构元素选取，本文滤波器选取余弦结构幅值为基波幅值的0. 5，元素长度为26，半圆结构幅值为基波幅值的0. 8，元素长度为60。对单相电压原始波形进行滤波的效果如图6所示，其中图6（a）为待测单相电压的原始波形，图6（b）为采用2阶Butterworth滤波器处理后的波形，图6（c）为本文滤波器滤波效果。

图6　两种滤波器的滤波效果对比

单相电压原始波形信噪比为25. 337 41dBW。通过对比图6中的滤波效果可知，使用二阶巴特沃斯低通滤波器和双结构的形态学滤波器滤波处理后波形的信噪比分别为26. 043 7 dBW和28. 834 3 dBW，两种滤波器都能滤除白噪声和脉冲噪声，前者造成的波形失真较大，并有相位延迟；后者还较好保留了原信号的基波特征，说明所提出的双结构形态学滤波器较为理想。

3. 2 单相电压暂降检测方法比较

用构造出的双结构数学形态学滤波器对含有5、7、11、13次谐波及噪声的电网单相电压进行预处理，将处理后的单相电压进行移相角δ为11. 25°的αβ⁃dq变换。由式（6）、式（7）可知，除了得到直流分量外还主要含有4、6、10、12次谐波，为准确地检测电压暂降发生的起止时间、暂降幅值和相角变化，用直线型结构元素形态学滤波器代替传统的二阶巴特沃斯低通滤波器对dq变换结果进行低通滤波。

直线结构元素的形态滤波器滤波效果由结构元素的宽度决定，综合考虑滤波效果和动态响应时间，结构元素的宽度选取为51。为验证本文方法的有效性，将本文方法与文献［6］中方法进行对比，得到图7的结果。

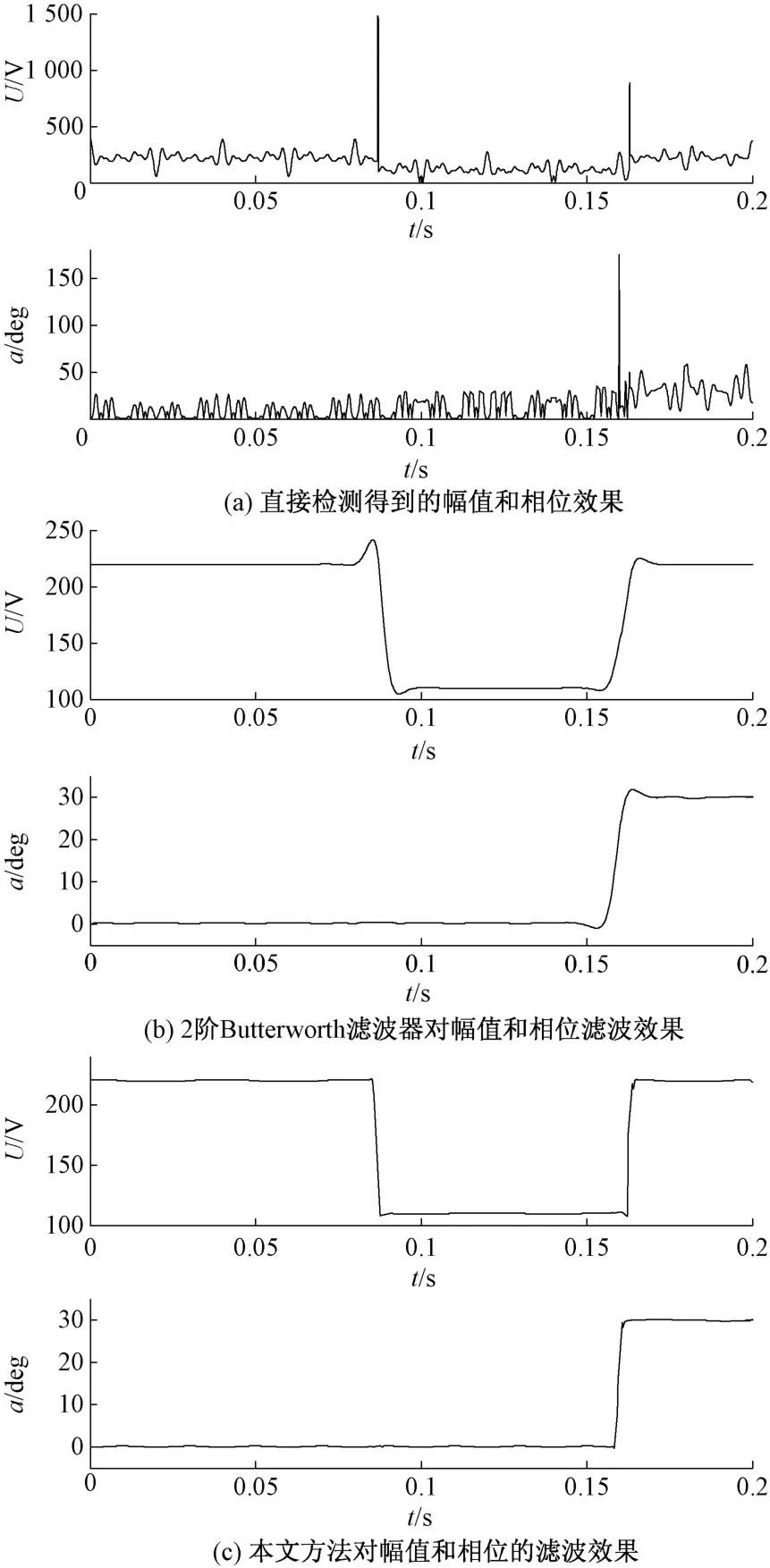
图7　两种滤波器对幅值和相位的滤波效果对比

由于检测方法本身对扰动的放大作用，使得在暂降检测的起止时刻均会出现“毛刺”现象，这会对DVR装置的补偿效果造成影响。由图7 （a）可知，直接对原信号进行检测，结果中得到的“毛刺”相当大，影响了检测结果的正确性。由图7（b）可知，传统的二阶巴特沃斯低通滤波器不能将“毛刺”有效滤除，影响检测的准确度，不仅给系统带来10 ms以上的滤波延时，滤波结果中还含有部分谐波，当谐波含量更高时，还会带来更大的滤波延时。由图7（c）可知，使用直线型结构元素形态学滤波器明显减小了“毛刺”现象，造成的系统延时大概1 ms，具有较好较快的滤波效果，不仅提高了系统的抗干扰能力，同时可以适当减小移相角从而提高检测的快速性。不过波形中仍含有少量低次谐波。提高直线型结构元素形态学滤波器的截止频率虽然会减小滤波延时，同时也会降低检测的准确度。基于数学形态学滤波的电压暂降检测方法已很好满足动态电压恢复器对电压暂降特征量检测的实时性和准确性要求。

4 结论

本文根据数学形态学滤波和移相小角度电压暂降检测方法的基础上，提出了一种使用双结构数学形态学滤波的快速电压暂降检测方法。即利用构造出的双结构数学形态学滤波器具有的良好非线性低通滤波特性，对电网单相电压中的谐波、噪声等干扰进行预处理后，将待测单相电压进行移相小角度的αβ⁃dq变换并用数学形态学滤波器代替传统的二阶巴特沃斯低通滤波器实现对非直流量的滤波，很好协调了检测的实时性与精确性之间的对立关系。实现实时、准确地检测电压暂降发生的起止时间、暂降幅值和相角变化。所用到的基波特征参考值实时得到，取代了锁相环节。该方法原理清晰、计算简单，避免了传统检测方法的缺点。仿真对比试验的结果表明该方法具有抗干扰能力强、检测延时小、检测结果准确性高，满足实时性和准确性的要求。

参考文献：

［1］李燕楠，包广清．基于小波包和支持向量机的电能质量扰动识别［J］．电力科学与工程，2012，28（3）：21－26．

［2］肖助力，龚仁喜，陈双．一种改进不完全S变换的电压暂降检测方法［J］．电力系统保护与控制，2015，（9）：62－68．

［3］潘进贤，邵振国．基于直觉模糊集熵测度的电压暂降源定位方法［J］．电力科学与工程，2015，31（1）：38－43．

［4］肖湘宁，徐永海，刘连光．考虑相位跳变的电压凹陷动态补偿控制器研究［J］．中国电机工程学报，2004，22（1）：64－69．

［5］杨亚飞，颜湘武，娄尧林．一种新的电压骤降特征量检测方法［J］．电力系统自动化，2004，28（2）：41 －44．

［6］张庆超，肖玉龙．一种改进的电压暂降检测方法［J］．电工技术学报，2006，21（2）：123－126．

［7］瞿硕，黄纯，江亚群，等．DVR电压暂降检测新方法［J］．电工技术学报，2013，28（4）：234－239．

［8］陈平，李庆民．基于数学形态学的数字滤波器设计与分析［J］．中国电机工程学报，2005，25（11）：60－65．

［9］丁宁，徐永海，肖湘宁．基于p－q－r变换和数学形态滤波的电压暂降检测算法［J］．电力自动化设备，2011，31（3）：89－93．

［10］黄耀东，张颖，韩子骞．基于数学形态滤波的电压闪变检测研究［J］．电力科学与工程，2014，30（8）：69－73．

［11］赵昭，刘利林，张承学，等．形态学滤波器结构元素选取原则研究与分析［J］．电力系统保护与控制，2009，（14）：21－25，35．

［12］谭智力，李勋，陈坚，等．基于简化p－q－r理论的统一电能质量调节器控制策略［J］．中国电机工程学报，2008，27（36）：85－91．

［13］崔红芬，李鹏，王畅．基于数学形态学的微网电压补偿量检测方法［J］．中国电机工程报，2013，33 （16）：122－128．

［14］王同勋，薛禹胜，CHOI S S．动态电压恢复器研究综述［J］．电力系统自动化，2007，31（9）：101－107．

Voltage Sag Detection Based on Mathematical Morphology Filtering Method

KANG Junsheng，LIU Guiying，LIAO Yaohua，LI Lin，FAN Feng
（College of Electrical and Information Engineering，Changsha University of Science＆Technology，Changsha 410114，China）

Abstract：A method using a double structure of mathematical morphology filter for fast voltage sag detection is pro⁃posed in this paper to meet the requirements of both real time property and accuracy for the voltage sag detection characteristics of the dynamic voltage restorer，which combines a small angle shifting in phase with αβ⁃dq trans⁃form．After being pretreated by the constructed double structure mathematical morphology filter，the single⁃phase voltage containing harmonics and noises shifted in phase with a little angle and then become two perpendicular and orthogonal αβ phase voltage．And then the αβ⁃dq transform is conducted and mathematical morphology filter is uti⁃lized to replace the traditional second⁃order butterworth low⁃pass filter to smooth the straight flow．By this method，the real⁃time and accurate detection of voltage sag start⁃stop time and temporary decline in value and phase angle change can be realized．To avoid delay and output error produced during lock process，the fundamental characteris⁃tics of the reference value are used to take place of the phase⁃locked loop section．The principle of the method is concise and simple．The advantages of anti⁃interference，small time delay and good accuracy of the method are demonstrated by the simulation results and tests．

Keywords：voltage sag；morphologic filter；phase⁃shifting angle；αβ⁃dq transform；simulation

作者简介：康军胜（1990－），男，硕士研究生，研究方向为电力系统运行与控制、电能质量监控等，E⁃mail：k＿junsheng ＠163. com。

收稿日期：2015－09－20。

中图分类号：TM73

文献标识码：A

DOI：10. 3969／j. issn. 1672-0792. 2016. 01. 012