基于双树复小波和ICA的电网谐波检测方法

马立新，项 庆，原晓琴（上海理工大学光电信息与计算机工程学院，上海200093）



基于双树复小波和ICA的电网谐波检测方法

马立新，项 庆，原晓琴
（上海理工大学光电信息与计算机工程学院，上海200093）

摘要：针对电网当中谐波严重的污染问题，提出一种基于双树复小波变换和ICA的电网谐波检测方法。该方法在不需要任何先验知识的情况下，先将混合的电网信号经过两个并行的实小波变换实现信号的分解和重构，得到各分量的最佳分解信号；结合ICA算法对分量信号继续进行盲源分离，解决了分解后频率混叠的问题，可以有效提取和分离电网谐波信息。相较于传统离散小波变换，双树复小波变换处理混合的电网信号时具有更低的频带能量泄露特性。通过仿真模拟电网谐波信号进行实验分析，表明了将双树复小波变换和ICA应用于电网谐波信息提取和分离的有效性。

关键词：电网谐波；双树复小波变换；ICA；谐波检测

0 引言

近些年，随着用电行业的不断发展，大量大功率的电力电子设备投入使用，向电网中注入的谐波也越来越多，致使电网信号的波形发生严重畸变，这些都会影响电网运行的可靠性和设备运行的效率。

当前电网中的谐波检测方法有很多，但都存在一些不足，如：加窗插值快速傅里叶变化（FFT），是目前应用最广泛的一种方法，但是无法实现与信号同步采样且频谱泄露严重，栅栏现象明显；传统离散小波变换虽具有良好的时频特性，但存在混频现象且频带能量泄露严重［1，2］；基于神经网络的谐波检测方法，需要训练大量的样本信号，实时性不好且频率泄露严重。

双树复小波变换具备了传统离散小波变换的优良特性，同时采用了双树滤波器的结构，可以保证信号的完全重构性，实现了信号分解时可以准确选择最佳层数，得到最佳分量，从而减少了频率混叠现象，降低了频带能量泄露，但是不能把频率混叠现象完全消除。独立成分分析（ICA）可以对多个独立信号构成的混合信号进行准确分离，但利用ICA模型，需要构造多路虚拟观测信号，最后通过ICA算法迭代求解。根据上述分析，本文提出了一种基于双树复小波变换和ICA的谐波检测方法。该方法将一路电网混合信号经过双树复小波分解、重构得分量信号，再结合ICA算法分离得到电网谐波分量信号。实验结果表明，该谐波检测方法频带能量消耗低，分解得到各分量无混频现象发生。

1 双树复小波变换

双树复小波变换［3－5］（Dual⁃Tree Complex Wavelet Transform，DT⁃CWT）是由Kingsbury提出并经后续学者的不断改进逐渐被运用到信号分解处理等领域。是采用两个并行的实小波变换实现信号的分解和重构，分别称之为实部树和虚部树，分解与重构过程如图1所示。

在信号分解及重构的整个过程中，虚部树的采样位置一直保持在实部树中间，使DT⁃CWT能够有效利用实部树和虚部树的小波分解系数，从而使得实部树信息交换和虚部树的信息交换互补。DT⁃CWT在处理混合信号时具有平移不变的特性，这样降低了很多有用信息丢失的概率。双树复小波变换在各层信号分解的过程中，利用小波系数二分法计算，有效避开复杂的代数运算，提高了算法运算的速度。

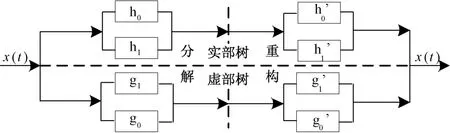
图1　双树复小波变换分解和重构过程

2 独立成分分析

独立成分分析［6－8］（ICA）是一种在未知源信号各个参数情况下，对源信号进行信号统计分析，仅根据观测信号的特性来恢复或者分离出源信号的信号处理算法。ICA估计分离的原理如图2所示。

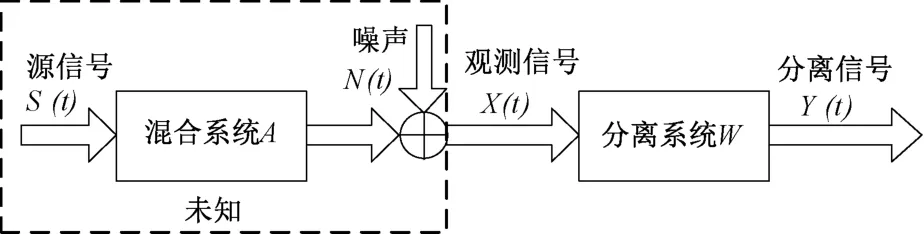
图2　ICA分离原理图

其算法可描述为：x1（t），x2（t），…，xm（t）是m个观测信号，由n个独立源信号s1（t），s2（t），…，sn（t）线性组合组合而成（m≥n），用矩阵表示为X（t）＝［x1（t），x2（t），…，xM（t）］，S（t）＝［s1（t），s2（t），…，sN（t）］，取A为m×n的混合矩阵，既是：

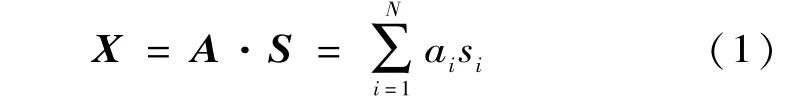
ICA算法进行迭代运算，设置合适的收敛值，最终得到一个分离的矩阵W，并使得：

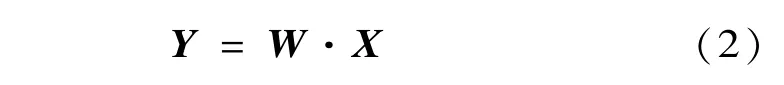
若输出信号yi（t）相互独立，则Y＝［y1（t），y2（t），…，yn（t）］就是S的估计值。

3 检测方法

3. 1 电网信号的数学表达式

电压信号可以表示为：

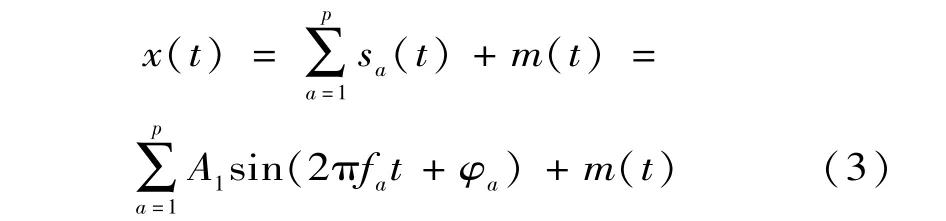
式中：x（t）为采样信号（总采样点数为n）；t为采样时间；p为所含的谐波个数；m（t）为白噪声项；Aa为a次谐波的幅值；fa为a次谐波的频率；φa为a次谐波的初始相位。

3. 2 DT⁃CWT对信号分解重构及去噪

根据以上对双树复小波的叙述，可以将其表示为［9，10］：

式中：φh（t），φg（t）表示为两个实小波；i表示为复数系数。

根据小波理论分析，需要求得上述两个实小波的小波系数和尺度系数。实部树小波变换的小波、尺度系数可由式（5）、（6）计算得：

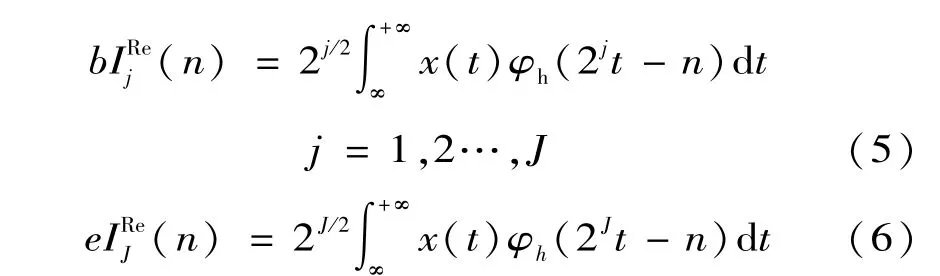
同理，下面虚部树小波变换的小波、尺度系数可分别由式（7）、（8）计算得：

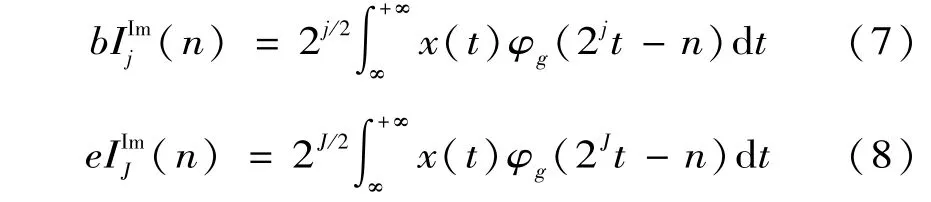
根据实部和虚部树小波系数和尺度系数计算，得到双树复小波变换的小波、尺度系数：

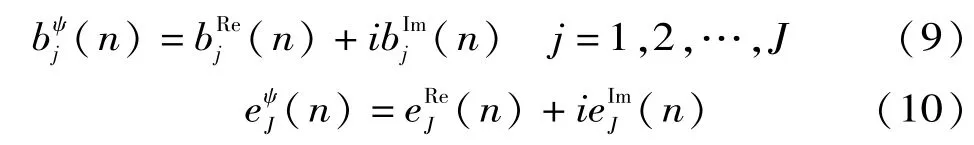
最后，重构后的双树复小波变换的小波系数、尺度系数如式（11）、（12）：

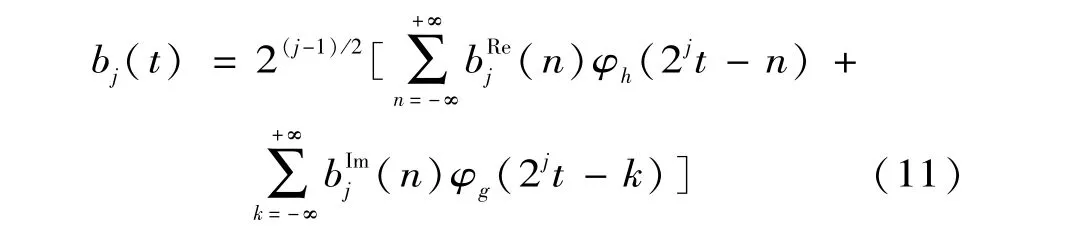
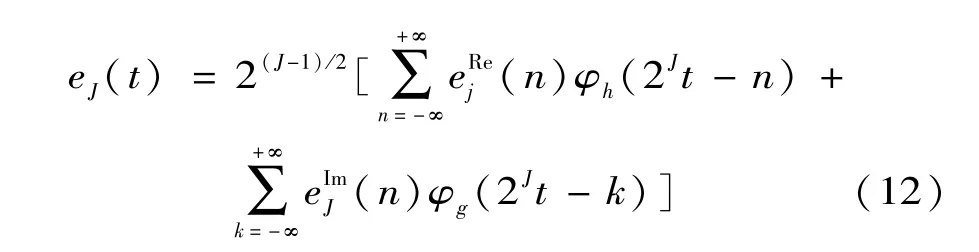
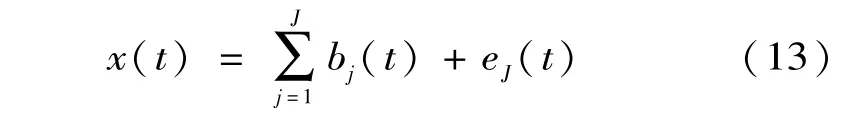
3. 3 ICA对信号的提取和分离

在ICA算法应用的模型中，有m个观测信号和n个独立源信号（n≤m）。通过上述双树复小波变换可得到一个由各分量组成的混合重构信号x（t），可以作为一路观测信号x1，若要应用ICA进行分析，还需构造（m－1）路观测信号，即：

最终重构、去噪后的信号可表示为：

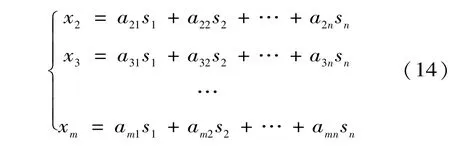
式中：aij（i＝1，2，…，m；j＝1，2，…，n）为混合矩阵系数。将观测信号的x1周期设为信号s1的周期，而信号s1的初始相位角可以根据采集点的初始位置确定。信号s2，s3，…，sn的频率可依次设为基波频率的整数倍，其中n的值可以根据实际的预估情况来确定。信号s2，s3，…，sn的初相角和系数可以任意取值，有些值可以用零代替，方便后续对构造的混合信号进行计算。

将得到的m路观测信号代入ICA算法，设置合适的收敛值进行迭代运算，最终可以获得分离矩阵W，这样便可分解混合信号x（t），得到各个独立信号的估计值。

3. 4 DT⁃CWT和ICA算法电网谐波检测过程

电网信号是一个各谐波源相互独立的混合信号，谐波含量多且不稳定，利用FFT非同步采样及传统小波变换运算，会出频带能量泄露严重，分解频带混叠等现象，利用双树复小波变换先对电网信号进行处理。复小波变换的相位谱具有丰富的相位变化信息，可据不同尺度信息变换相位、变化周期确定各分量的相位及幅值信息。双树复小波变换对电网信号进行分解、去噪、重构可得到混合重构信号x（t）。将此混合信号构造m路观测信号，再代入ICA算法中进行迭代运算求出分离矩阵W，即可得到重构信号x（t）的各独立分量的估计值。检测过程如图3所示。

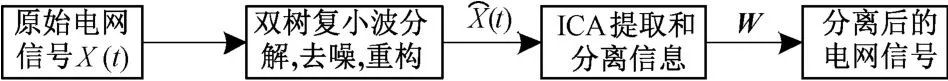
图3　DT⁃CWT和ICA算法电网谐波检测过程

图4　传统小波分解后信号的波形及频谱

4 仿真分析

根据电网谐波的特点，构造被检测的混合信号为：

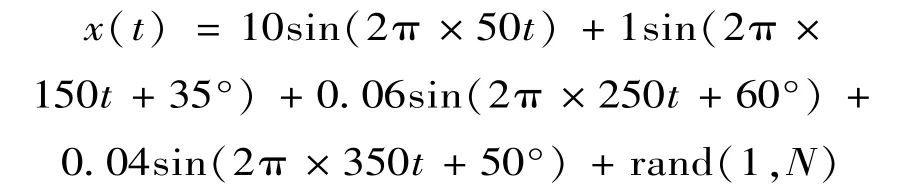
其中设置基波频率为50 Hz，其中还含有150 Hz、250 Hz、350 Hz的高次谐波成分及随机噪声rand（1，N）。该仿真信号的采样频率设置为1kHz，采样点数设为1 000点，分别进行两层小波分解。图4为采用db3小波2层分解后的波形及频谱。从图中右侧频谱监视窗口可以看出：分解后各分量的频率混叠较为严重，同时还出现了70 Hz，170 Hz等虚假频率信号。在仿真过程中传统小波2层分解参数选取随意度高，对仿真结果有一小部分的影响。图5为双树复小波对模拟仿真信号进行2层分解后的波形及频谱，对比图1，可以看出各分量信息频谱混叠明显减少且分解效果提升很多，但分解后的信号还是存在部分的频率混叠。图6为结合ICA算法对DT⁃CWT分解后得到的各个分量所组成的混合信号进行独立成分分析，可以看出各分量频率信号独立性非常好，不存在频率混叠现象。

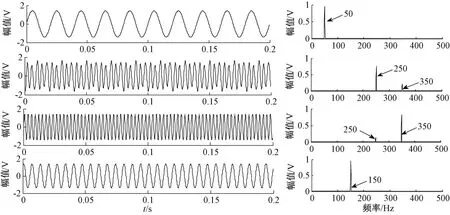
图5　DT⁃CWT分解后信号的波形及频谱

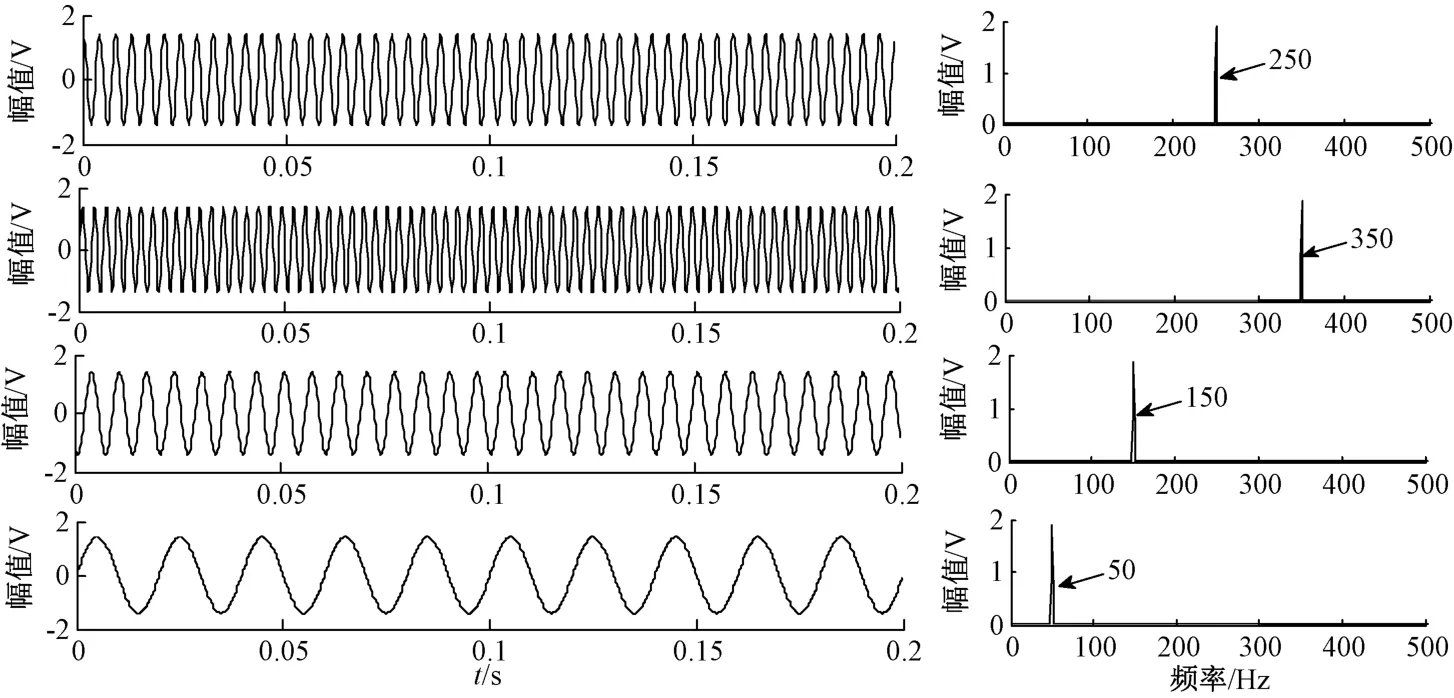
图6　结合ICA分解后信号的波形及频谱

分析分解后的4个分量频带能量泄露情况如图7所示。可以看出：双树复小波变换在分解处理各个频率信号较传统小波变换能量泄露很少。

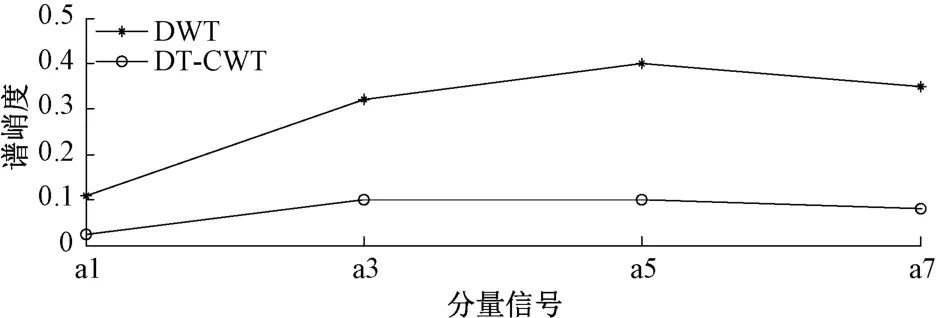
图7　分解各分量能量消耗

5 结论

（1）本文在综述比较常见的几种谐波检测方法的基础上，分析DT⁃CWT理论和ICA算法，提出了DT⁃CWT和ICA的谐波检测方法，并对该算法进行了仿真验证。

（2）从对含3、5、7次谐波及随机噪声信号的电网信号仿真可以看出：DT⁃CWT分解电网混合信号得到各个分量相对于传统离散小波变换在频率混叠方面改善很多，但仍存在一定的混频问题，结合ICA算法对DT⁃CWT得到的重构信号继续进行独立成分分析，消除了混频现象。

（3）双树复小波变换和传统离散小波变化在分解时存在频带能量泄露问题做了定量分析，更加证明了双树复小波变换具有较低的频带能量泄露。

参考文献：

［1］周林，夏雪，万蕴杰，等．基于小波变换的谐波检测方法综述［J］．电工技术学报，2006，21（9）：67－74．

［2］段虎．基于小波包变换的谐波检测系统的研究［D］．湖南：长沙理工大学，2012．

［3］胥永刚，赵国亮，候少飞．双树复小波／包变换在机械故障诊断中的应用研究［J］．振动与冲击，2014，33（增刊）：106－115．

［4］陈彬强，张周锁，何正嘉．双密度双树复小波变换及其在机械在故障诊断微弱特征提取中应用的应用［J］．机械工程学报，2012，48（9）：56－63．

［5］EDWARD H S L，PICKERING M R，FRATER M R，et al．Image segmentation from scale and rotation invariant texture features from the double dyadic dual⁃tree complex wavelet transform［J］．Image and vision computing，2011，29（1）：15－28．

［6］孟玲玲，孙常栋，王晓东．基于特征值分解和独立分量分析的谐波／间谐波检测方法［J］．电力系统自动化，2012，36（5）：61－66．

［7］安连锁，冯强，沈国清，等．基于盲源分离的电站锅炉多源泄漏点位研究［J］．华北电力大学学报（自然科学版），2015，42（5）：69－79．

［8］AAPO H，JUHA K，Erkki，周宗潭译．独立成分分析［M］．北京：电子工业出版社，2014．

［9］郝文广，丁常富，梁娜．小波降噪与FFT降噪比较［J］．电力科学与工程，2011，27（3）：59－61．

［10］吴一全，纪守新，尹丹艳．双树复小波和独立分量分析的红外小目标检测［J］．兵工学报，2010，31 （11）：1431－1437．

A Power Grid Harmonic Detection Method Based on Dual Tree Complex Wavelet and ICA

MA Lixin，XIANG Qing，YUAN Xiaoqin
（School of Optical⁃electrical and Computer Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China）

Abstract：To solve the problem of power grid harmonic pollution，a method based on dual tree complex wavelet transform and ICA grid harmonic detection is proposed．The signal decomposition and reconstruction is realized by transforming the hybrid grid signals with two parallel solid wavelets，and then the optimal decomposed signal can be acquired without any prior knowledge．The problem of the decomposed frequency aliasing is solved by utilizing the method of blind source separation combined with the ICA algorithm towards the component signals．Information of the power grid harmonics is abstracted and separated with great efficiency．Compared with the traditional discrete wavelet transform，when dealing with hybrid grid signals，the dual tree complex wavelet transform has the feature of lower frequency band energy leakage．The validity of the proposed method is verified by the simulation and tests．

Keywords：power grid harmonic；dual tree complex wavelet transform；ICA；harmonic

作者简介：马立新（1960-），男，教授，主要研究方向为配电网规划与优化配置、电力电子与电力传动、电力负荷需求分析与预测方法、调速系统智能控制等，E⁃mail：malx＿aii＠sina．com。

基金项目：上海市张江国家自主创新重点项目（201310⁃PI⁃B2⁃008）；沪江基金（C14002）。

收稿日期：2015－10－20。

中图分类号：TM714

文献标识码：A

DOI：10. 3969／j. issn. 1672-0792. 2016. 01. 011