基于结构可靠性算法的停车换乘行程时间可靠性计算
李 伟 周菁楠 周 峰 徐瑞华
(1同济大学道路与交通工程教育部重点实验室,上海 201804)(2上海市交通港航发展研究中心,上海 200030)
基于结构可靠性算法的停车换乘行程时间可靠性计算
李伟1周菁楠2周峰1徐瑞华1
(1同济大学道路与交通工程教育部重点实验室,上海201804)
(2上海市交通港航发展研究中心,上海200030)
摘要:为了定量分析停车换乘(P&R)出行方式的时间可靠性,提出了一种P&R行程时间可靠性计算算法并进行求解.将P&R出行过程按照出行特征划分为小汽车、停车搜索、步行及轨道交通4个出行子链,在拟合和标定各子链行程时间分布的基础上,基于结构可靠性计算中的HL-RF算法设计求解算法.通过当量正态化法(RF)将各出行子链的行程时间分布转换为对应的当量正态分布,然后利用验算点法(HL)计算P&R行程时间可靠度.最后,以实际案例验证所提算法.结果表明,该算法能够简洁有效地计算P&R出行行程时间可靠性,且计算中考虑了P&R各出行子链行程时间服从不同时间分布的情况.
关键词:城市交通;停车换乘; HL-RF算法;可靠性
引用本文:李伟,周菁楠,周峰,等.基于结构可靠性算法的停车换乘行程时间可靠性计算[J].东南大学学报(自然科学版),2016,46(1) : 226-230.DOI: 10.3969/j.issn.1001-0505.2016.01.037.
近年来由于城市交通状况恶化,交通拥堵加剧,交通运行状态与出行者期望间的差异日益扩大,迫使人们从更理性化的高度看待交通问题,可靠性作为一个重要概念被引入交通领域,成为近10年来交通学者们广泛关注的问题之一[1-2].停车换乘(P&R)出行通过将富有灵活性的小汽车与可靠性高的地铁交通相结合,为通勤者和其他进入市中心的出行者提供了一种新的出行选择,能够避免中心区交通拥挤的压力以及紧张昂贵的停车资源.但是,不同于传统出行方式,P&R出行涉及到3种出行方式及中间的换乘过程,其时间分布特征更为复杂,导致可靠性难以定量计算.
传统的交通可靠性分析方法主要有概率方法和仿真方法两大类.其中,概率方法多应用于具有相同分布特征的道路路段行程时间可靠性评价,着重行程时间分布的拟合,并利用概率统计计算90 或95分位值、缓冲时间、计划时间等可靠性指标[3-4].但是对于包含小汽车、地铁、停车等多个子过程的P&R多方式换乘出行而言,其行程时间具有比单一道路行程时间更为复杂的随机性和波动性,难以用单一分布函数表达其复杂的出行全程的时间特征,导致基于概率方法推导P&R可靠性及指标的计算过程繁杂且难以求解.区别于概率方法,文献[5-6]采用仿真方法模拟路网变化对可靠性的影响,主要思路为:先计算不同路径或路段的出行阻抗,根据交通需求进行随机网络交通分配,利用网络均衡算法求解各路径或路段的最终均衡流量及其行程时间,继而得到不同出行方式下的行程时间可靠性.然而,这种仿真方法求解P&R行程时间可靠性仅适用于理想化的试验网络,难以模拟存在不同影响因素的实际交通网络.鉴于此,本文在分析与构建P&R出行行程时间的基础上,根据结构可靠性计算中常用的Hasofer-Lind-Rackwitz-Fiessler(HL-RF)算法[7-8]设计相应算法,分析计算P&R行程时间可靠性.
1 P&R出行过程
P&R出行过程可以描述为:通勤者从起点驾车到P&R停车场,搜索停车泊位停车,步行到轨道交通车站,乘坐轨道交通以及从轨道交通车站步行到目的地的全部过程.据此将P&R出行链划分为4个子链:小汽车出行子链、停车搜索子链、轨道交通出行子链和步行子链(见图1).以不同层面的交通网络来表示P&R出行是一种多方式换乘出行模式.

图1 P&R出行过程
根据交通网络可靠性的定义,将P&R行程时间可靠性定义为出行者在一定的出行时间预算内完成计划内P&R出行全过程的概率,可表示为
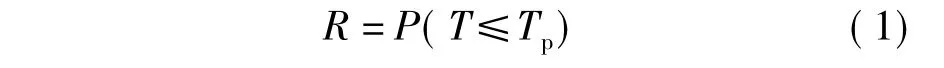
式中,P()为概率函数; T为通勤者实际出行时间; Tp为通勤者预计出行时间.
P&R出行总时间T为各子链行程时间总和,即

式中,Ta,Ts,Tw,Tm分别为小汽车出行子链、停车搜索子链、步行子链、轨道交通出行子链的行程时间.
小汽车出行子链的行程时间是指出行者从起点驾车至P&R停车场耗费的时间.以往的研究通常从理论上假设路段行程时间服从某种特定分布,但由于受不同道路条件、交通状况的影响,小汽车的行程时间也会呈现出不同的分布[9],因此需要根据实际数据拟合获得.
停车搜索子链的行程时间是指通勤者从到达P&R停车场开始搜索空闲泊位到完成停放操作的时间.文献[6,10]指出,停车搜索时间与停车需求V和停车场容量C有关,可利用类似BPR函数的形式方程求解,即

式中,dj为停车搜索时间; d0为自由停车搜索时间;α,β为待标定的参数.
步行子链的行程时间是指通勤者在换乘过程中花费在走路步行上的时间,一般服从正态分布,即
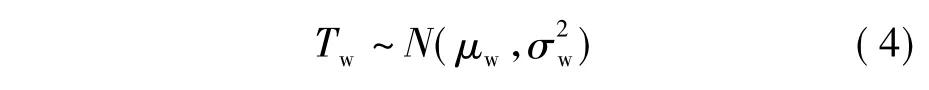
式中,μw,σw分别为步行时间的期望和标准差.
轨道交通出行子链由进站步行、候车、乘车、换乘步行以及出站步行等过程组成.其行程时间主要包括步行时间、候车等待时间和在途时间,即
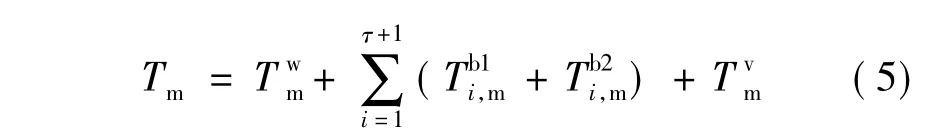
2 P&R行程时间可靠性求解算法
P&R出行过程由多个出行子链构成,且每个出行子链服从不同分布,故本文借鉴结构可靠性计算中的HL-RF算法对P&R行程时间可靠性设计求解算法.HL-RF算法的优点在于,不仅能够近似计算具有多个不同随机变量的系统结构可靠度,而且考虑了实际中随机变量服从非正态分布的情况[7-8].算法包括2个部分:①将非正态随机变量转换为正态随机变量的当量正态化(RF变换) ;②求解可靠性指标的验算点法(HL法).
HL-RF算法中,整个系统的性能或状态可以用功能函数或状态方程g(x) = g(x1,x2,…,xi,…,xn)来描述,其中x为系统各组成部分的向量形式,xi为系统各组成部分,且xi间相互独立.将状态方程引申到P&R出行方式中,xi可以表示P&R出行过程的各出行子链.按照HL法的思想[7],可靠性指标η为坐标原点至临界状态曲面g(x) =0的最短距离,可以根据如下的非线性约束最优化问题求解可靠性指标:

式中,q(x)为坐标原点至临界状态曲面的距离.
系统可靠性R可以通过下式求得:
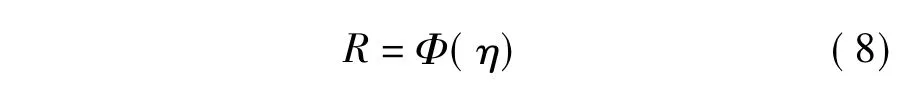
式中,Φ()为标准正态分布的累积分布函数.
2.1当量正态化法
HL-RF算法中,x中的任意随机变量xi均应服从正态分布.但在现实问题中,并非所有变量xi都服从正态分布,需采用RF法[8]将非正态随机变量转化为正态随机变量,得到等效标准正态分布(也称当量标准正态分布)的均值μi和标准差σi.其基本思路是,寻找一个服从正态分布N(μi,σ2i)的随机变量,使其在设计试验点处与非正态随机变量xi具有相同的概率和累计概率密度,利用这个服从正态分布的随机变量来代替非正态随机变量.转化公式为[8]
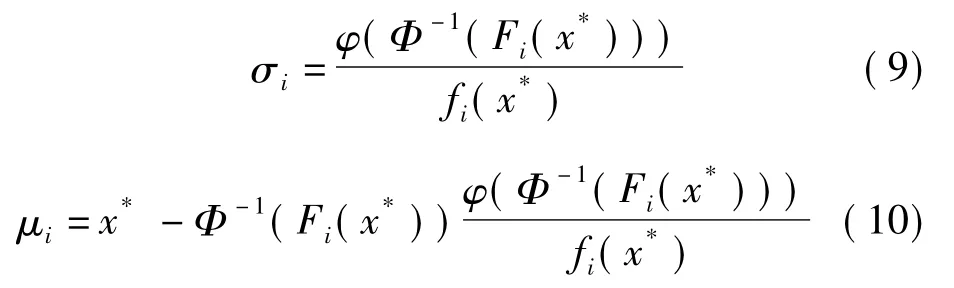
式中,x*为基准点处变量xi的值; Fi(),fi()分别为原分布的累积分布函数和概率分布函数;φ()为标准正态分布的概率分布函数.
2.2验算点法
式(6)和(7)说明求解可靠性指标η是非线性规划问题,直接求解存在困难.HL法采用一维线性搜索算法求解.设x(k +1)为第k +1次迭代的点,η(k +1)为点x(k +1)到原点的距离,则有
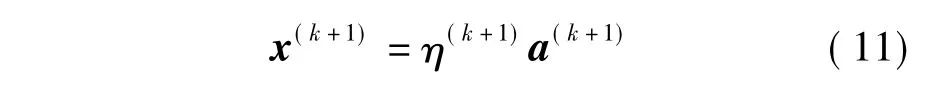
式中,a(k +1)为第k + 1次迭代临界状态方程g(x) =0的负梯度方向,且
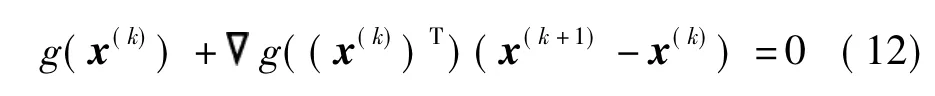
同时,P&R系统的各子链间以串联形式连通,即总行程时间为各子链行程时间的叠加.临界状态方程还可表示为
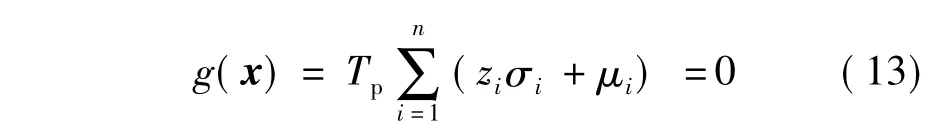
式中,zi为随机变量xi变换后的标准正态分布变量.
将式(11)和(13)代入式(12)可得

可以看出,式(14)中每次迭代的η均相同.故P&R行程时间可靠度可以统一表示为
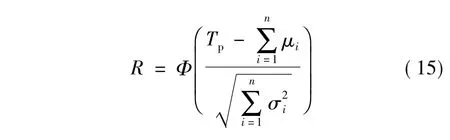
综上,算法计算流程如下:
①分别拟合与标定4个子链的行程时间分布;
②采用当量正态化变换法,根据式(9)和(10)将各分布转化为等效正态分布变量,得到等效的标准化正态分布期望与标准差;
③根据式(15)计算P&R可靠性指标η以及行程时间可靠度R.
3 案例计算
3.1案例参数
为了验证所提算法的有效性,以上海郊区某P&R设施为例进行分析计算.调查得到某通勤者的起讫点及出行路径如图2所示.通勤者的出发点(家)位于市郊区(点Q),P&R停车场位于距离出发地最近的一处地铁沿线车站附近(点D),通勤者的目的地(工作地点)位于市中心CBD区域(点C),通勤者需要乘坐地铁Ⅰ线和Ⅱ线,点A和点B分别表示2处不同地铁车站,期间需要换乘1次.在此案例背景下进行实地调研及问卷调查.
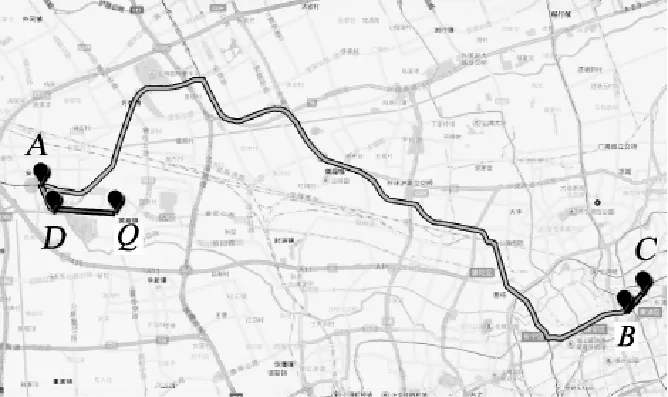
图2 通勤者P&R出行路径
为了获取可靠性评价模型所需要的参数,对P&R出行方式中各子链出行时间进行数据采集,得到各时间参数取值.
首先,对点Q到点D间小汽车出行路段进行数据调查,调查时段为周三早高峰时段(07: 00—08: 30),记录从点Q到点D间小汽车的行程时间,得到50组浮动车实测数据.对实测调查数据进行频数分析,利用Matlab软件中的Distribution Fitting Tool工具箱对数据进行分布拟合,得到的拟合曲线如图3所示.由图可知,在4种常用的概率分布中,对数正态分布的拟合效果较好.采用对数正态分布对数据进行K-S检验,接受数据服从对数正态分布的零假设.因此,小汽车子链出行时间服从如下的对数正态分布:
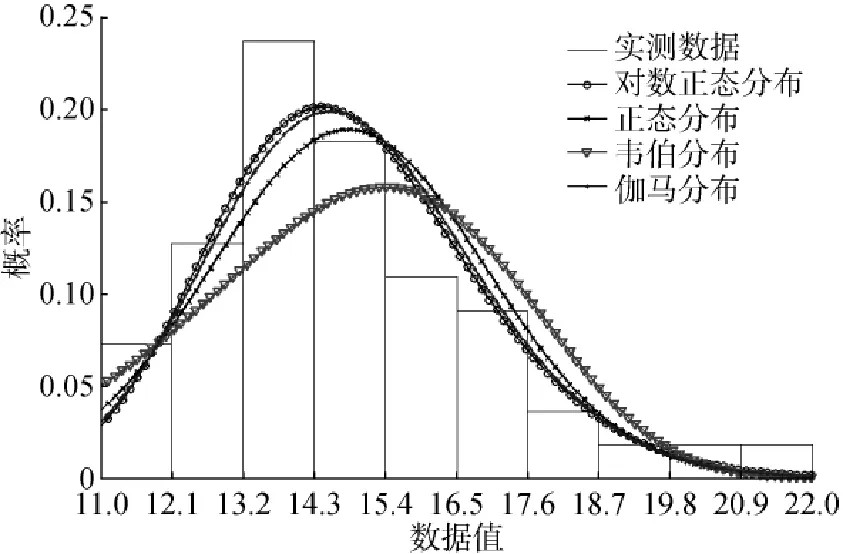
图3 路段实测数据概率分布曲线
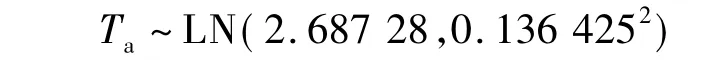
式中,LN()为对数正态分布函数.
停车场的停车搜索时间函数可利用停车场提供的调查日泊位占用率及调查所得的停车搜索时间来进行参数标定.调查日(周三)泊位占用情况(包括入场、出场车辆数)从停车场管理部门获得,结果如图4所示.停车搜索时间则依据调查人员跟随入库车辆直至其完成停车过程记录下的花费时间获得,记录入场时间与停车完成时间共同构成一条完整数据,调查日早高峰共采集52条停车数据.
利用Matlab软件中的Curve Fitting Tool工具箱对采集数据与式(3)进行最小二乘法曲线拟合,得到停车搜索时间期望值为


图4 P&R停车场泊位占用率及停车搜索时间
式中,停车场目前停放车辆数V与通勤者到达停车场的时间有关.
然而通勤者的停车位搜索时间并不固定,而是一个随机数值.对实际调查数据进行进一步处理,将调查时间段按15 min划分,对比根据公式计算出的停车搜索时间理论值与实际调查值.数据处理结果显示,均方根误差与理论值的比值随时间段的变化差别较小.故通勤者早高峰时段停车搜索时间的均方根误差σ可表示为

由此可以认为在短时间(15 min)内通勤者的停车搜索时间服从正态分布,即

在步行子链中,根据调查人员反馈的实地调查数据,通勤者于P&R出行过程中花费在步行上的时间服从如下的正态分布:

在轨道交通出行子链中,需经过2条线路:地铁Ⅰ线和Ⅱ线.地铁Ⅰ线连接市区与郊区,是一条典型的郊区线路,早高峰时间段车站A的列车发车间隔为9 min,同理Ⅱ线上的车站B的列车发车间隔为3.4 min.通勤者由车站A到达车站B需要换乘1次,因此τ=1,在换乘站的拥挤度取历史数据λ=0.2.此外,通勤者地铁的总在途乘车时间为31 min.
3.2可靠度计算
通过实际调查数据拟合得到4个出行子链行程时间的概率分布和累积分布后,需要对这4个出行子链的行程时间分布进行当量正态化处理,转换基准点选取各子链的期望值,结果见表1,其中停车搜索过程与步行过程无需当量正态化转换.由此便可计算得出P&R行程时间可靠度与计划出行时间之间的关系(见图5).由图可知,随着计划出行时间的增加,通勤者的P&R行程时间可靠度呈S形上升趋势.
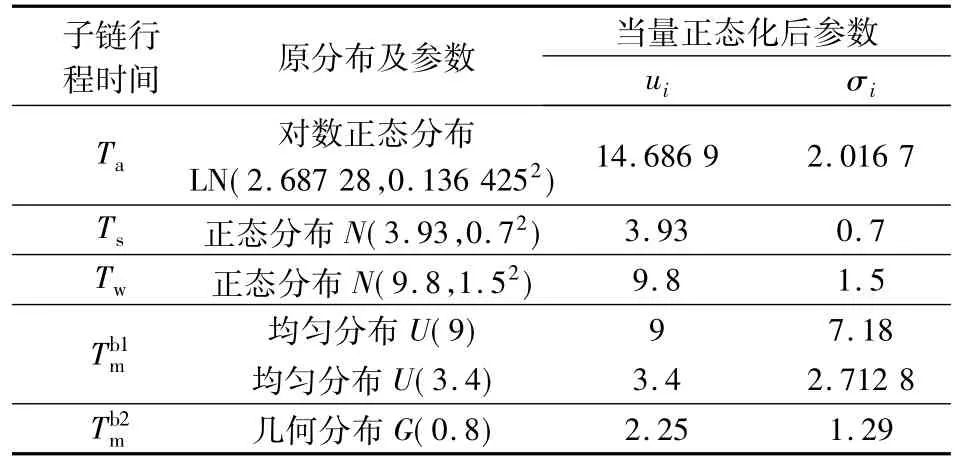
表1 当量正态化计算表
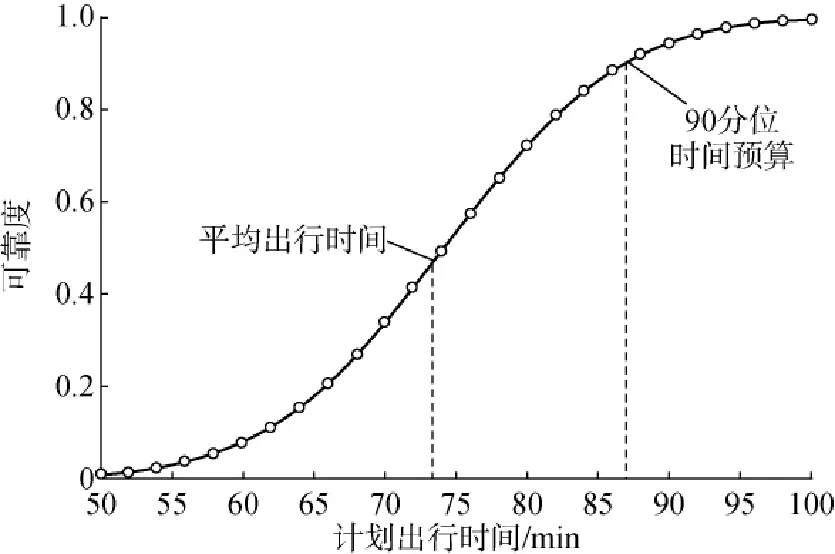
图5 P&R行程时间可靠度曲线图
P&R行程时间可靠性评价指标如下:
1)期望行程时间.即出行者选择本路径出行的平均花费时间E,其计算公式为
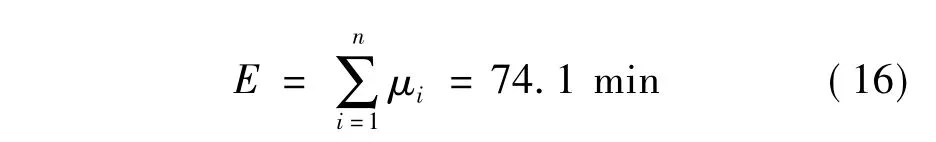
由此可知,通勤者利用P&R方式出行的期望行程时间为74.1 min(见图5).
2)预留时间.为保证准点到达目的地的概率足够大,出行者花费在路径出行上的时间总和T(r)为
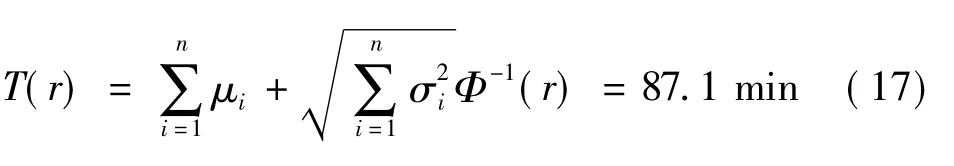
假设准点到达目的地的概率r =90%,则通勤者的预留时间为87.1 min(见图5).
3)缓冲时间.为保证准点到达目的地的概率足够大,出行者需要额外的出行时间Tr(r),其计算公式为
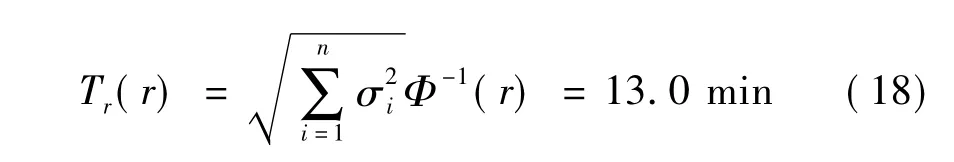
假设准点到达目的地的概率为90%,可得通勤者所需要的缓冲时间为13.0 min.这意味着通勤者为保证尽可能上班不迟到,需要较平均出行时间多13 min的提前出发时间或早到等待时间.
4 结语
本文针对P&R出行过程提出了一种定量分析行程时间可靠性的算法,借鉴结构可靠性计算中的HL-RF算法,对P&R行程时间可靠性进行算法设计,通过实际案例来说明算法流程.案例分析结果表明,该算法能够有效地解决P&R出行模式中的各出行子链服从不同行程时间分布以及子链行程时间分布服从非正态分布的问题.下一步需要深入分析各出行子链之间的相关性,考察各子链相关性对P&R行程时间可靠性的影响.
参考文献(References)
[1]Lam T C,Small K A.The value of time and reliability: Measurement from a value pricing experiment[J].Transportation Research Part E,2001,37(2) : 231-251.
[2]Tilahun N Y,Levinson D M.A moment of time: Reliability in route choice using stated preference[J].Intelligent Transportation System,2010,14(3) : 179-187.
[3]Mine H,Kawai H.Mathematics for reliability analysis [M].Tokyo: Asakura-Shoten,1982: 2-15.
[4]Milkovits M N.Simulating service reliability of a high frequency bus route using automatically collected data [D].Cambridge,MA,USA: Massachusetts Institute of Technology,2008.
[5]陶骏杰,张勇.多方式交通网络的时间可靠性分析[J].交通运输系统工程与信息,2015,15(2) :216-222.Tao Junjie,Zhang Yong.Time reliability analysis of multi-modal transportation networks[J].Journal of Transportation Systems Engineering and Information Technology,2015,15(2) : 216-222.(in Chinese)
[6]范文博.基于地铁的停车换乘可靠性分析[J].交通运输系统工程与信息,2013,13(2) : 57-62,198.DOI: 10.3969/j.issn.1009-6744.2013.02.009.Fan Wenbo.Metro-based park and ride reliability analysis[J].Journal of Transportation Systems Engineering and Information Technology,2013,13 (2) : 57-62,198.DOI: 10.3969/j.issn.1009-6744.2013.02.009.(in Chinese)
[7]Yang S,Malik A,Wu Y J.Travel time reliability using Hasofer-Lind-Rackwitz-Fiessler algorithm and kernel density estimation[J].Transportation Research Record: Journal of the Transportation Research Board,2014,2442: 85-95.
[8]Rackwitz R,Flessler B.Structural reliability under combined random load sequences[J].Computers&Structures,1978,9(5) : 489-494.
[9]Emam E B,Ai-Deek H.Using real-life dual-loop detector data to develop new methodology for estimating freeway travel time reliability[J].Transportation Research Record: Journal of the Transportation Research Board,2006,1959: 140-150.
[10]Lam W H K,Li Z C,Huang H J,et al.Modeling time-dependent travel choice problems in road networks with multiple user classes and multiple parking facilities[J].Transportation Research Part B: Methodological,2006,40(5) : 368-395.
Calculation of travel time reliability of park-and-ride based on structural reliability algorithm
Li Wei1Zhou Jingnan2Zhou Feng1Xu Ruihua1
(1Key Laboratory of Road and Traffic Engineering of Ministry of Education,Tongji University,Shanghai 201804,China)
(2Shanghai Transportation and Ports Development Research Center,Shanghai 200030,China)
Abstract:In order to quantitatively analyze the travel time reliability of park-and-ride (P&R) trips,a solution algorithm is proposed and solved.The P&R trip is divided into four subchains,including auto,parking search,walk,and metro.Based on the fitting and calibration of the travel time distribution of each subchain,the Hasofer-Lind-Rackwitz-Fiessler (HL-RF) algorithm,widely used in the calculation of structural reliability,is used to design a solution algorithm.First,the travel time distribution of each subchain is converted to the corresponding normal distribution according to the RF method.Then,the HL method is used to calculate the travel time reliability of the P&R trip.Finally,a case is used to prove the effectiveness of the proposed algorithm.The results show that this algorithm can concisely and efficiently calculate the travel time reliability of the P&R trip.In the calculation,the cases for travel time of subchains following different distributions are considered.
Key words:urban traffic; park and ride (P&R) ; Hasofer-Lind-Rackwitz-Fiessler (HL-RF) algorithm;reliability
基金项目:国家自然科学基金资助项目(71271153)、中国博士后科学基金资助项目(2014M551454)、浙江省自然科学基金资助项目(LQ13G010010).
收稿日期:2015-07-27.
作者简介:李伟(1989—),男,博士生;徐瑞华(联系人),男,博士,教授,博士生导师,rhxu@ tongji.edu.cn.
DOI:10.3969/j.issn.1001-0505.2016.01.037
中图分类号:U491
文献标志码:A
文章编号:1001-0505(2016) 01-0226-05

