隔震桥梁合理结构阻尼模型

夏修身　陈兴冲　李建中

(1兰州交通大学土木工程学院，兰州　730070)(2同济大学土木工程学院，上海　200092)



隔震桥梁合理结构阻尼模型

夏修身1陈兴冲1李建中2

(1兰州交通大学土木工程学院，兰州730070)
(2同济大学土木工程学院，上海200092)

摘要:为了更好地处理隔震桥梁中的复杂阻尼问题，探讨了隔震桥梁中阻尼的模拟方法．根据阻尼的来源及作用机制不同，将隔震桥梁的阻尼分为滞回阻尼与结构阻尼两类．基于统一振型阻尼比的振型叠加法，给出了采用瑞利阻尼模拟结构阻尼时控制振型的选取方法．以支座位移与墩底内力作为复合指标，以无结构阻尼的地震反应作为参照，考查了采用瑞利阻尼与刚度比例阻尼时隔震桥梁的地震反应．结果表明，结构阻尼对隔震桥梁中的地震反应有较大的影响，经典的瑞利阻尼不适于隔震桥梁，利用初始刚度比例阻尼来模拟隔震桥梁的结构阻尼相对比较合理．

关键词:桥梁;隔震;阻尼

引用本文:夏修身，陈兴冲，李建中．隔震桥梁合理结构阻尼模型［J］．东南大学学报(自然科学版)，2016，46(1) : 140－145．DOI: 10．3969/ j．issn．1001－0505．2016．01．023．

机械工程、航天工程及土木工程都涉及到阻尼问题．机械工程中通常采用润滑方式来减小阻尼的不利作用;航天工程中则通过控制算法、不断修正航天器的轨道数据来纠正阻尼的影响;土木工程中，通常希望结构中具有一定的阻尼能耗散地震能量，对于结构阻尼相对较小的大跨度钢桥还可附加阻尼装置来减小结构的地震反应．

与刚度不同，阻尼不能由构件的尺寸及其材料特性等进行精细理论计算，只能宏观表达［1－3］．实际结构中的阻尼是多种复杂阻尼机制的组合，但一般采用统一的数学模型进行模拟［4］，故常用的阻尼模型都是对特定情况下阻尼问题的近似等效处理，存在适用条件．尽管阻尼是客观存在的，但结构中的阻尼作用与其采用的数学模型及等效原则有关［1］．线弹性结构侧重于关注地震反应的最大值，模态阻尼比和经典比例阻尼模型均可较好地处理结构地震反应中的阻尼问题［4－5］．隔震桥梁的显著特点是墩梁间的联系减弱、基本自振周期较长，地震中梁体近似为刚体振动［6］，其结构中的阻尼也有其自身的分布特点．随着减、隔震装置在桥梁中的大量应用，基于线弹性动力分析理论与最大反应量的阻尼模型已不能适应当前的需求．

本文基于隔震桥梁的阻尼来源与作用机理分析，探讨了隔震桥梁中结构阻尼的模拟方法，为隔震桥梁地震反应分析提供依据．

1　阻尼来源及作用机制

结构地震反应中阻尼主要来源包括结构材料内摩擦、干摩擦、空气阻尼、地基土内摩擦、地基中波的辐射耗能、人工耗能装置(减、隔震支座与阻尼器)、结构构件的塑性耗能、地基土的塑性耗能［2－3］．根据产生机理又可将上述阻尼分为材料阻尼、黏滞阻尼与界面阻尼三大类．

材料阻尼是指由结构材料的分子之间或晶粒界面之间的错动、滑移等引起的耗散能量，与材料类型及材料中的应力状态有关．界面阻尼反映了结构构件连接处及支撑部位的摩擦耗能、混凝土微裂缝的开启与闭合的耗能，是弹性结构中阻尼的主要来源之一．黏滞阻尼是指与黏滞性流体或空气接触的结构在振动过程中的能量耗散．空气阻尼耗能约占总阻尼耗能的1%，可以忽略［2］．结构振动时，基础与地基土的接触面之间会产生应力波，应力波带到地基中的振动能量即为辐射阻尼［7］．桥梁结构地震反应分析中通常偏保守地忽略辐射阻尼影响或将其纳入到结构阻尼中综合考虑．阻尼将机械能转化为热能，作用机理复杂．结构地震反应分析的目的是获取结构的反应量，而不是对阻尼作用机制的解释，故选择阻尼模型时更侧重于使用上的方便．

结构阻尼主要来源于材料阻尼与界面阻尼［8］．结构构件的塑性耗能，地基土的塑性耗能，减、隔震装置与附加阻尼装置的耗能在宏观上都表现为滞回阻尼的耗能，地震反应分析时通常将滞回阻尼从结构的总阻尼中分离出来单独考虑［9－10］．需要说明的是，下文所提到的结构阻尼均指已分离出滞回阻尼后剩下的结构阻尼．通常情况下，隔震桥梁的塑性主要集中在减、隔震装置中，其结构中的阻尼分成滞回阻尼与结构阻尼来考虑．

2　瑞利阻尼

2. 1物理意义

基于实测的模态阻尼比，采用振型叠加法得到的结构弹性地震反应具有较高的精度．在弹塑性状态下，由于结构的振型不固定，经典的振型分析方法不适用，需要建立比例阻尼矩阵，通过逐步积分来求解结构的地震反应．由于振型矩阵对质量矩阵、刚度矩阵具有正交性，故建立比例阻尼矩阵C最简单的方法是使其与质量矩阵M或刚度矩阵K成线性比例关系［11］．经典比例阻尼包括质量比例阻尼、刚度比例阻尼与瑞利(Rayleigh)阻尼［4－5］．

质量比例阻尼的表达式为

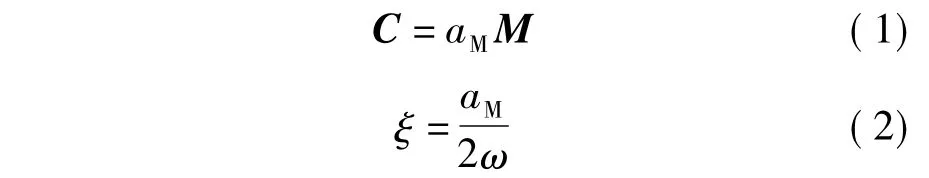
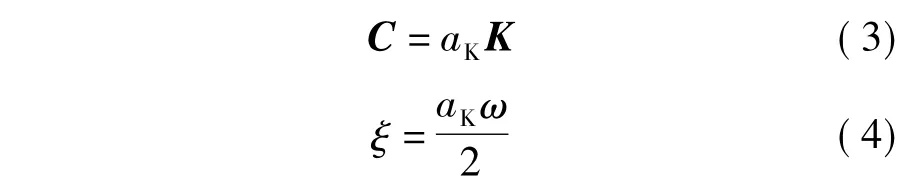
式中，aK，aM为比例系数;ξ为振型阻尼比;ω为自振频率．

质量比例阻尼的阻尼比与频率成反比;刚度比例阻尼的阻尼比与频率成正比．将刚度比例阻尼或质量比例阻尼用于单自由度地震反应分析时，通过合理地选择比例系数aK或aM，可以较好地模拟实际结构中的阻尼，但其不适用于主要振型中频率范围很宽的多自由度结构，这是因为不合适的阻尼比会使不同振型的相对幅值发生严重畸变．当阻尼取刚度比例阻尼与质量比例阻尼的组合时，问题则可以得到明显改进［5］．

瑞利阻尼为刚度比例阻尼与质量比例阻尼的线性组合［4］，即

瑞利阻尼中，刚度比例阻尼表示结构中各自由度之间通过线性黏滞阻尼器互联，质量比例阻尼表示为结构与外部约束之间用线性黏滞阻尼器互联．由微观的黏弹介质本构关系可知，在实际结构中考虑质量比例阻尼并不合理．结构动力分析中考虑质量比例阻尼，是因为它可以增强对允许模态阻尼比的控制［12］．

式(5)中比例系数aK与aM的确定需要指定2个频率(振型)．图1为瑞利阻尼的振型阻尼比与频率的关系曲线．图中，ξmax，ξmin分别为频率ωc与Rωc之间的最大、最小阻尼比，其中，R为系数．由

刚度比例阻尼的表达式为图可知，在2个频率之间的振型具有较低的阻尼比，曲线最低点之后的阻尼比随频率的增加而增大，高频率对应高阻尼比．如果控制振型选择不当，高阶振型的反应将因其具有高阻尼而被消除［5］．

图1　振型阻尼比与自振频率的关系

瑞利阻尼与实际结构阻尼缺少一致性．当瑞利阻尼的质量比例系数aM与刚度比例系数aK选取不合理时，会使得各振型对应的阻尼比波动较大，与实际不符，给地震反应结果带来较大的误差．

瑞利阻尼满足振型正交条件、使用方便，且普通结构的阻尼小，选取合适控制振型时瑞利阻尼的模拟精度在工程上是可以接受的，故瑞利阻尼被广泛应用于桥梁结构中［3，11］．

2. 2使用方法

现行的动力学教材中关于瑞利阻尼中比例系数选取方法较少，可操作性不强．下面介绍桥梁地震反应分析中瑞利阻尼中比例系数确定时控制振型的选取方法［12］．

瑞利阻尼使用正确的前提是计算分析模型中最大与最小振型的阻尼比相差较小．如果比例系数aM，aK已知，则瑞利阻尼中的振型阻尼比可按下式计算:

假定选取基振型与第n阶振型为控制振型，基本自振频率为ω，第n阶的自振频率为Rω．为了判别控制振型选取是否合适，引入阻尼比边界Δ，即

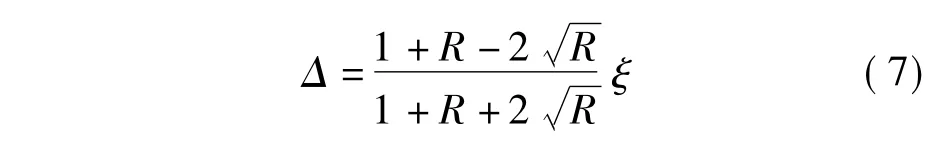
式中，ξ为地震反应分析中指定的阻尼比，钢筋混凝土结构通常取ξ=5%．

如果R取值较大，且Δ相对于ξ来说较小，则可以按下式计算比例系数:

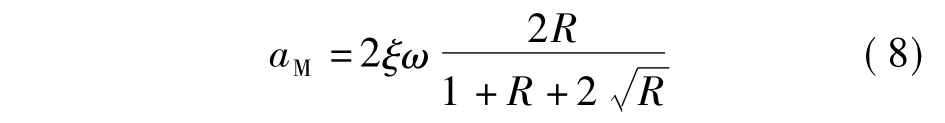
此时，按式(6)模拟结构中的阻尼比较合理．

R较大时，Δ相对于ξ来说也较大，故需要将R减小为第n－1阶的自振频率与基率的比值，重新计算Δ和ξ．

3　隔震桥梁中的阻尼模拟

利用延长桥梁结构自振周期来降低地震反应的措施可统称为隔震．桥梁可以在支座处与墩底处进行隔震，且支座减隔震技术在工程中应用较多．常用的减隔震支座包括板式橡胶支座、铅芯橡胶支座与摩擦摆式支座等．板式橡胶支座通过增加结构柔性(延长周期)来降低桥墩中的地震反应，使各桥墩实现协同抗震．铅芯橡胶支座除了具有板式橡胶支座的优点外，还在支座中增加了阻尼，以降低支座的位移需求．摩擦摆式支座主要通过墩梁之间沿曲面的滑动来实现隔震，此外，支座的滑动摩擦还增加了结构阻尼．板式橡胶支座与铅芯橡胶支座的竖向承载能力有限，且多用于中小跨度桥梁，摩擦摆式支座则具有较高的竖向承载能力，可用在大跨度桥梁中［6］．

隔震桥梁系统不满足比例阻尼的适用条件［3］，常用的阻尼模拟方法为:将滞回阻尼从结构总阻尼中分离出来单独考虑，余下的结构阻尼采用比例阻尼近似模拟［13］，采用逐步积分法来求解系统的地震反应．需要说明的是，隔震桥梁的刚度随时间变化，其结构的比例阻尼矩阵可以有多种形式．

3. 1算例分析

图2　动力分析模型

本文以某桥4 m×35 m等截面连续箱梁为例，梁高为2 m，单箱五室截面．双柱式矩形截面桥墩，1. 2 m直径桩基础．其动力分析模型见图2．图中，PM01为桥台，PM03墩为制动墩．抗震设防烈度为8度，基本地震动峰值加速度为0. 2g，按《城市桥梁抗震设计规范》中的丙类设防，Ⅱ类场地，反应谱特征周期为0. 35 s．采用MIDAS/CIVIL软件建立动力计算模型．主梁、桥墩、承台及桩基采用弹性空间梁单元模拟．土对桩的约束采用分布弹簧模拟，弹簧的刚度用m法计算．普通支座为盆式橡胶支座，减、隔震支座为摩擦摆式支座．采用主从理想约束模拟普通支座，采用非线性支座单元模拟摩擦摆式支座．地震反应分析中输入了基于《城市桥梁抗震设计规范》反应谱人工合成的3条地震波w1，w2，w3．

3. 2普通支座桥梁的结构阻尼模拟

以振型叠加法的结果作为瑞利阻尼比例系数的选择标准［14］．为了验证瑞利阻尼的使用方法，在进行普通支座桥梁地震反应分析时，采用振型叠加法，各振型的阻尼比均为5%．前800阶振型的总参与质量超过95%，计算结果见表1．

表1　振型叠加法的计算结果

结构第1阶振型为制动墩的顺桥向弯曲振动，对应的自振频率ω= 7. 85 rad/s，第153阶振型对应的自振频率约为61ω．选取第1阶与第153阶为控制振型，指定ξ= 0. 05．此时R = 61，Δ= 0. 6ξ，Δ相对于ξ偏大，其计算结果与振型叠加法结果差别较大，需减小R，重新计算Δ．经试算可知，第12阶振型对墩柱的地震反应有贡献，其自振频率约为8ω，则R =8，按式(5)求得Δ=0. 23ξ，结果可接受．此时，比例系数aM=0. 857 s－1，aK=0. 001 7 s．计算结果见表2．

对比表1和表2可知，振型叠加法的计算结果大于基于瑞利阻尼的计算结果，这是因为振型叠加法中各振型的阻尼比均为5%，且考虑了超过95%的振型贡献．而在基于瑞利阻尼的计算中，高阶振型对应较大的阻尼比，而较大阻尼比会减小高阶振型的贡献．总体来看，基于瑞利阻尼的计算结果已接近振型叠加法的计算结果，具有工程可接受的精度．

3. 3隔震桥梁的阻尼模拟

支座减隔震桥梁的桥墩及基础通常要保持基本弹性状态，此时结构中的阻尼主要为减、隔震装置的附加阻尼(滞回阻尼)与结构阻尼．如果桥墩与基础允许进入非弹性状态，还应考虑桥墩与基础的滞回阻尼．将减、隔震支座的附加阻尼从总阻尼中分离出来单独考虑;如摩擦摆式支座，其阻尼作用通过其恢复力模型的滞回耗能来体现，摩擦摆支座的恢复力模型来源于试验，其滞回耗能与实际阻尼作用较接近．本文重点探讨隔震桥梁中的结构阻尼模拟问题．

将3. 1节算例中的墩(台)支座全部改成摩擦摆支座，其他条件保持不变．各墩摩擦摆支座的曲率半径为4 m、滑动摩擦系数为0. 03．摩擦摆支座采用双线性恢复力模型［6］．下面讨论瑞利阻尼、刚度比例阻尼与无结构阻尼的隔震桥梁地震反应．

隔震桥梁具有初始刚度与屈服后刚度，刚度比例阻尼既可采用初始刚度又可采用屈服后的刚度［13］，故本文分以下4个工况进行计算:

1)使用瑞利阻尼，按普通支座的自振特性值，aM=0. 857 s－1，aK=0. 001 7 s;

2)使用初始刚度比例阻尼，采用结构的初始刚度，取普通支座的基频，比例系数aK=0. 012 7 s;

3)使用屈服刚度比例阻尼，采用结构的隔震刚度Kfps，隔震结构基频ωe= 1. 55 rad/s［15］，比例系数aK=0. 064 5 s;

4)无结构阻尼．

4　结果分析

鉴于设计者比较关注隔震桥梁的墩底弯矩、剪力与支座位移，选取墩底内力与支座位移作为考查指标．3条输入地震波下PM02～PM04墩底弯矩、剪力计算结果见表3．输入地震波w2下PM03墩底弯矩时程曲线见图3．输入地震波w3下PM03墩顶的支座位移比较见表4．输入地震波w2下PM03墩顶的支座水平位移时程曲线见图4;由于PM02，PM04与PM03的支座位移较接近且变化规律一致，故其结果不再单独列出．

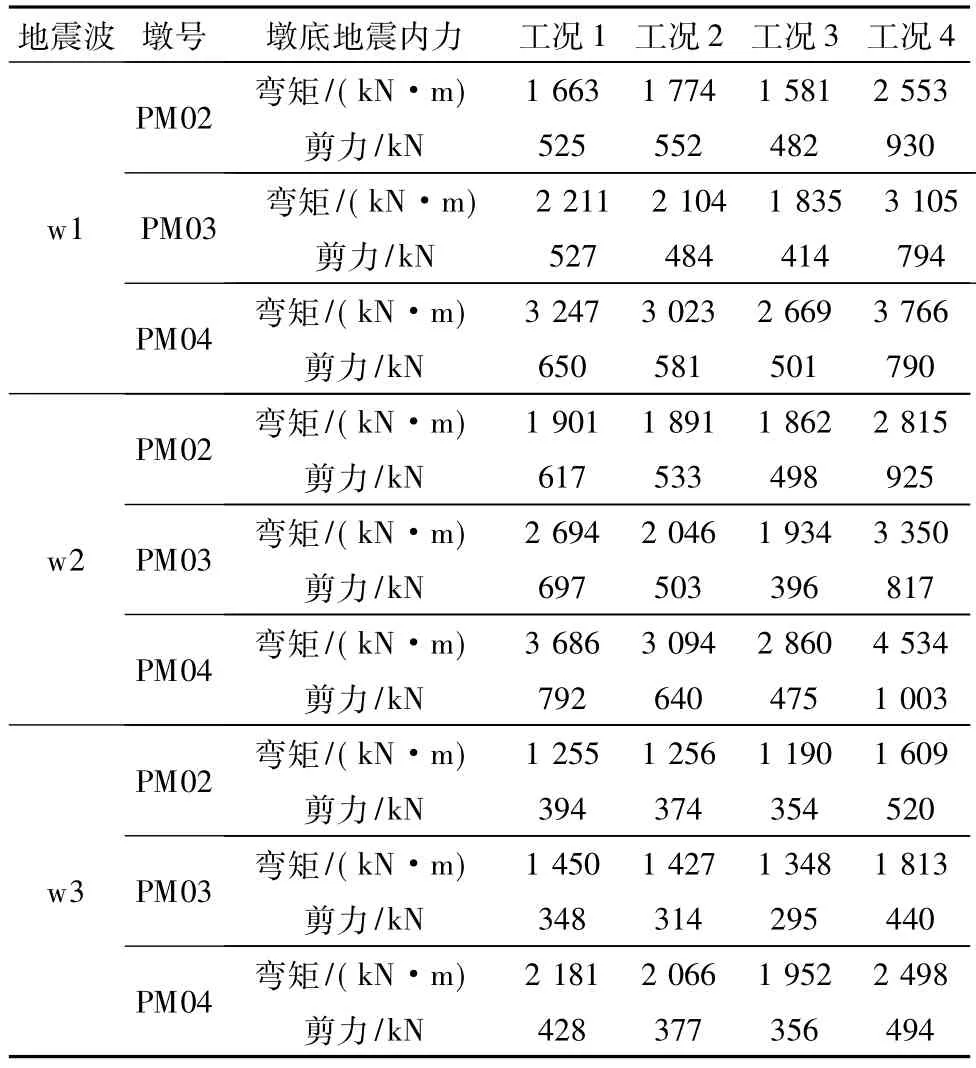
表3　4种工况下的墩底弯矩及剪力

由表3可以看出，工况4下墩底弯矩与剪力明显大于工况1～工况3，表明隔震桥梁中的结构阻尼具有一定的耗能作用，不考虑结构阻尼耗能作用的情况偏于保守．由图3可知，瑞利阻尼、初始刚度比例阻尼、屈服刚度比例阻尼与无结构阻尼的时程曲线形状都比较接近，表明结构阻尼对时程曲线的形状影响较小．有结构阻尼的时程曲线较无结构阻尼时光滑，表明阻尼作用表现为减小了时程曲线上的毛刺点数量．对本桥而言，不存在减隔震装置附加阻尼为主、结构阻尼为辅、结构阻尼作用较小的情况．工况2与工况3的结果较接近，这是因为隔震桥梁的墩梁间联系较弱，梁体刚度远大于桥墩及减隔震系统的组合刚度，地震中梁体类似刚体移动，隔震桥梁系统类似于单自由度体系，第1阶振型及其振型阻尼对地震反应的贡献较大，故两者差异相对较小．

从表3中还可看出，工况1下的墩底弯矩及墩底剪力最大，工况3最小，工况2介于两者之间，这与工况1下结构阻尼最大、工况3最小、工况2介于两者之间相对应，说明对本桥而言，结构的地震反应随结构阻尼的增大而增大．然而，工况4下无结构阻尼的地震反应明显大于有阻尼情况，工况2下的弯矩与剪力大于工况1，说明结构阻尼可减小结构的地震反应．地震反应随结构阻尼的增大而增大，无结构阻尼的地震反应大于有结构阻尼的地震反应，该现象突显了结构阻尼作用机理的复杂性．

图3　w2下PM03墩底弯矩时程曲线

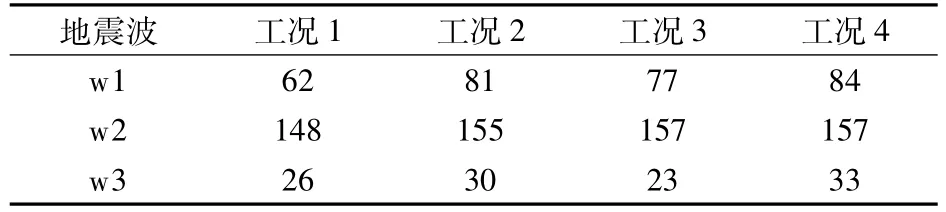
表4　PM03墩顶支座位移比较mm

图4　w2下PM03墩顶支座水平位移时程曲线

由表4可以看出，工况1的支座位移最小，工况4最大，工况2与工况3介于两者之间，但与工况4相近，与工况1相差较大，且3条输入地震波下具有相同的规律．究其原因在于，结构阻尼具有一定的耗能作用，工况4没考虑结构阻尼，故其支座位移最大;瑞利阻尼中包含了刚度和质量对阻尼的贡献，故其支座位移最小．虽然在实际结构中考虑质量比例阻尼不合理，但在结构动力分析中考虑质量比例阻尼，可以增强对指定模态阻尼比的控制．对于普通支座桥梁而言，受固定支座作用，制动墩与梁体连接密切，整个结构体系为典型的多自由度体系，此时利用质量比例阻尼加强对指定模态阻尼比的控制比较合理;然而，隔震桥梁的隔震支座减弱了墩梁间的联系，梁相对于墩会产生较大位移，整个结构体系可近似成单自由度体系，此时在结构阻尼中再考虑质量比例阻尼则会人为加大隔震桥梁的结构阻尼，从而低估支座位移的地震需求．从图4可以看出，工况2，3与工况4的支座位移时程曲线较工况1更接近．因此，隔震桥梁的结构阻尼部分不应有质量比组成部分．

由表4可见，工况2中2条输入地震波下的支座位移与工况4接近，而工况3只有1条输入地震波下的支座位移与工况4接近，表明初始刚度比例阻尼的结果更接近无结构阻尼．由表3可知，工况3的墩底弯矩与工况2较接近，略小于工况2，表明屈服刚度比例阻尼得到的墩底弯矩、剪力小于初始刚度比例阻尼．即采用初始刚度比例阻尼得到的墩底弯矩与剪力对设计而言偏于安全．因此，隔震桥梁的结构阻尼采用初始刚度比例阻尼来模拟较合理．

5　结论

1)隔震桥梁中的结构阻尼具有一定的耗能作用，对结构的地震反应有较大影响，需要加以考虑．

2)隔震桥梁墩梁之间联系减弱，由于质量比例阻尼组成部分的存在，采用经典的瑞利阻尼会低估支座位移的地震需求，不适用于隔震桥梁．

3)采用初始刚度比例阻尼来模拟隔震桥梁的结构阻尼相对合理．

参考文献(References)

［1］黄宗明，白绍良，赖明．结构地震反应时程分析中的阻尼评述［J］．地震工程与工程振动，1996，16(2) : 95－104．Huang Zongming，Bai Shaoliang，Lai Ming．Review of the damping in earthquake response time-history analysis of structures［J］．Earthquake Engineering and Engineering Vibration，1996，16(2) : 95－104．(in Chinese)

［2］董军，邓洪洲，王肇民．结构动力分析阻尼模型研究［J］．世界地震工程，2000，16(4) : 63－69．DOI: 10. 3969/j．issn．1007－6069. 2000. 04. 012．Dong Jun，Deng Hongzhou，Wang Zhaomin．Studies on the damping models for structural dynamic time history analysis［J］．World Information on Earthquake Engineering，2000，16 (4) : 63－69．DOI: 10. 3969/j．issn．1007－6069. 2000. 04. 012．(in Chinese)

［3］彭伟．减隔震桥梁非经典阻尼问题与简化分析方法［D］．上海:同济大学土木工程学院，2006．

［4］Chopra A K．Dynamics of structures: theory and applications to earthquake engineering［M］．2nd ed．Beijing: Higher Education Press，2007: 455－458．

［5］克拉夫R，彭津J．结构动力学［M］．2版．王光远，译．北京:高等教育出版社，2006: 184－185．

［6］夏修身，崔靓波，陈兴冲，等．超长联大跨连续梁桥隔震技术应用研究［J］．桥梁建设，2015，45(4) : 39－45．Xia Xiushen，Cui Liangbo，Chen Xingchong，et al．Seismic isolation technology for long span and super long unit continuous beam bridge［J］．Bridge Construction，2015，45(4) : 39－45．(in Chinese)

［7］杨军，宋二祥，陈肇元．桩在饱和土中水平振动的辐射阻尼简化算法［J］．岩土力学，2002，23(2) : 179－183．DOI: 10. 3969/j．issn．1000－7598. 2002. 02. 009．Yang Jun，Song Erxiang，Chen Zhaoyuan．Simple radiation damping model for horizontally vibrating pile in saturated soil［J］．Rock and Soil Mechanics，2002，23 (2 ) : 179－183．DOI: 10. 3969/j．issn．1000－7598. 2002. 02. 009．(in Chinese)

［8］Kareem A，Gurley K．Damping in structures: its evaluation and treatment of uncertainty［J］．Journal of Wind Engineering and Industrial Aerodynamics，1996，59 (2) : 131－157．

［9］Soong T T，Spencer B F．Supplemental energy dissipation: state-of-the-art and state-of-the-practice［J］．Engineering Structures，2002，24 (3) : 243－259．DOI: 10. 1016/S0141－0296(01) 00092－X．

［10］Symans M D，Charney F A，Whittaker A S，et al．Energy dissipation systems for seismic applications: current practice and recent developments［J］．Journal of Structural Engineering，2008，134(1) : 3－21．

［11］刘晶波，杜修力．结构动力学［M］．北京:机械工业出版社，2005: 119－122．

［12］Hall J F．Problems encountered from the use (or misuse) of Rayleigh damping［J］．Earthquake Engineering＆Structural Dynamics，2006，35(5) : 525－545．

［13］Jehel P，Léger P，Ibrahimbegovic A．Initial versus tangent stiffness-based Rayleigh damping in inelastic time history seismic analyses［J］．Earthquake Engineering＆Structural Dynamics，2014，43(3) : 467－484．

［14］楼梦麟，张静．大跨度拱桥地震反应分析中阻尼模型的讨论［J］．振动与冲击，2009，28(5) : 22－26．DOI: 10. 3969/j．issn．1000－3835. 2009. 05. 006．Lou Menglin，Zhang Jing．Discussion on damping models for seismic response analysis of long-span bridge［J］．Journal of Vibration and Shock，2009，28 (5 ) : 22－26．DOI: 10. 3969/j．issn．1000－3835. 2009. 05. 006．(in Chinese)

［15］彭天波，李建中，范立础．双曲面球型减隔震支座的开发及应用［J］．同济大学学报(自然科学版)，2007，35(2) : 176－180．Peng Tianbo，Li Jianzhong，Fan Lichu．Development and application of double spherical aseismic bearing ［J］．Journal of Tongji University(Natural Science)，2007，35(2) : 176－180．(in Chinese)

Reasonable structure damping model of isolated bridge

Xia Xiushen1Chen Xingchong1Li Jianzhong2
(1School of Civil Engineering，Lanzhou Jiaotong University，Lanzhou 730070，China)
(2College of Civil Engineering，Tongji University，Shanghai 200092，China)

Abstract:In order to deal with the complex damping problems in isolated bridges，the damping simulation methods are studied．According to different damping sources and mechanisms，the damping in isolated bridges is divided into two categories，the hysteretic damping and the structural damping．The selection method for the controlling mode with structure damping simulated using Rayleigh damping is proposed based on the mode superposition method with the uniform mode．Taking the seismic response without structural damping as reference，the seismic responses of an isolated bridge with Rayleigh damping and stiffness proportional damping are investigated by using the bearing displacement and the internal force of pier bottom as composite index．The results show that structural damping has great influence on the seismic response of the isolated bridge．The classical Rayleigh damping is not suitable for the isolated bridge．Using stiffness proportional damping based on the initial stiffness to simulate structure damping in the isolated bridge is reasonable．

Key words:bridge; earthquake isolation;damping

基金项目:国家自然科学基金资助项目(51268033)、长江学者和创新团队发展计划资助项目(IRT1139)．

收稿日期:2015-06-26．

作者简介:夏修身(1978—)，男，博士，副教授，xiaxiushen@ mail．lzjtu．cn．

DOI:10．3969/j．issn．1001－0505．2016．01．023

中图分类号:U442. 55

文献标志码:A

文章编号:1001－0505(2016) 01-0140-06