旋转流场中颗粒群的运动特性

陈云富　张程宾　陈永平

(东南大学能源热转换及其过程测控教育部重点实验室，南京　210096)(东南大学能源与环境学院，南京210096)



旋转流场中颗粒群的运动特性

陈云富张程宾陈永平

(东南大学能源热转换及其过程测控教育部重点实验室，南京210096)(东南大学能源与环境学院，南京210096)

摘要:建立了颗粒群在部分充液旋转容器内水相中运动的非稳态理论模型并进行数值模拟，研究了旋转流场中颗粒群的运动特性．分析了旋转容器内流场、颗粒群演化、颗粒运行轨迹及液体黏度和颗粒密度对颗粒群在水相中分散性能的影响．通过将数值模拟得到的流场中颗粒及速度分布与文献实验数据进行对比，验证了所建立理论模型的合理性．研究结果表明:在旋转容器内水相流场中存在涡流，颗粒群在旋转流场及涡流的作用下运动并逐渐分散至整个水相区域．随着液体黏度的增加，颗粒群在旋转容器内水相中分布更加均匀;颗粒密度的增加，导致颗粒分散驱动力下降，使得颗粒群聚集在水相的旋出侧附近．

关键词:颗粒; VOF-DEM;旋转流场;分散

引用本文:陈云富，张程宾，陈永平．旋转流场中颗粒群的运动特性［J］．东南大学学报(自然科学版)，2016，46(1) : 76－80．DOI: 10．3969/ j．issn．1001－0505．2016．01．013．

固液两相流广泛存在于化工、食品、制药等领域中，固体颗粒运动是固液两相流研究的重要问题之一［1－2］．运动过程中，由多个颗粒所构成的颗粒群在旋转流场中的运动与分散受到浮力、重力、曳力、马格努斯力等多种作用力的作用，同时还与颗粒间以及颗粒和容器壁面间的相互碰撞相关．

近年来，国内外已就旋转流场中颗粒群的运动及分散行为开展了一些理论和实验研究，特别是对搅拌槽内液相中颗粒群的运动及分散行为进行了较为深入的分析．Wadnerkar等［3］利用欧拉－欧拉多相流模型对搅拌槽内固液流动进行了仿真，分析了搅拌槽内流体速度分布及固体颗粒浓度分布．Tamburini等［4］利用欧拉－欧拉多流体模型分析了不同叶轮转速及颗粒初始浓度对搅拌槽内液相中颗粒分布的影响．李良超等［5］采用CFD方法对搅拌槽内轻密度颗粒群运动特性进行数值模拟，考察了轻密度颗粒在搅拌槽内速度场、颗粒浓度分布规律等．然而，目前很少采用欧拉－拉格朗日方法对旋转流场中颗粒群的运动及分散特性进行研究．相对于欧拉－欧拉方法，拉格朗日方法能够追踪单个固体颗粒的运动轨迹，有利于理解颗粒的运动特性，而典型的拉格朗日方法DEM(discrete element method)能有效地模拟颗粒群的运动［6－8］．

相对于搅拌槽内液相中颗粒群运动研究，目前对于含有自由表面的部分充液旋转容器内颗粒群运动特性的研究还较少．Sakai等［9］和Sun等［10－11］利用DEM模拟了二维与三维旋转圆筒内具有自由表面的液相中颗粒群运动，分析了输入参数(弹性恢复常数和摩擦系数)、润滑力和虚拟质量力对固体颗粒宏观行为及固体颗粒床动力学行为的影响．但是，这些研究大都集中于重颗粒在旋转圆筒内的运动行为．与重颗粒在旋转流场中运动不同，固体颗粒密度与液体密度相当的颗粒群在旋转流场中能够较好地扩散并跟随液体运动，且液面对液体中固体颗粒的运动行为也有一定的影响．目前，针对固液密度相当的颗粒群在具有自由表面的旋转圆筒内液相中的运动及分散特性尚缺乏深入认识．

为此，本文基于VOF(volume of fluid)相界面追踪方法模拟具有相界面运动的水相和气相流场，采用DEM模拟颗粒在水相中的运动，同时采用软球模型考虑颗粒间及颗粒与壁面间的碰撞，建立了颗粒群在部分充液旋转容器中运动的理论模型，并进行了数值求解．研究了颗粒群在旋转流场中的运动与分散特性，分析了颗粒液体密度比、液体黏度对液体中固体颗粒分散特性的影响．

1　数学模型

本文研究颗粒群在部分充液旋转圆柱形容器内的运动特性．图1给出了颗粒群在旋转圆柱形容器内运动的工作示意图，圆柱形容器(直径D = 195 mm)中充入了一定量的液体水(水相高度H = 84 mm，密度ρl= 1 000 kg /m3)，水中含有一定数量的圆形颗粒．考虑到圆柱形容器为轴对称且容器长度L远大于直径D，为简化数值计算以减少运算量，采用圆柱形容器的二维结构作为计算区域．计算中，颗粒直径di= 1. 5 mm，颗粒密度ρi= 1 100 kg /m3，颗粒数量为404．

图1　颗粒群在容器内运动的工作示意图

1. 1气液界面追踪

旋转容器内水相外部为单相连续气相，假设气相为不可压缩的黏性流体，采用标准的N-S方程求解．而在水相中由于存在颗粒群，采用修正的NS方程求解．水相运动过程中受到颗粒的反作用力，因此，在方程中引入该作用力．

水相与气相之间存在气液界面，气相与水相界面轮廓变化及运动用VOF方法描述［12］，由连续表面力模型计算得到气液界面的表面张力［13］;在每个单元内气液两相满足αg+αl=1，其中，αg，αl分别为气相、液相体积率．当αg=1时，计算网格中充满气相;当αg=0时，计算网格中充满水相;当0＜αg＜1时，计算网格处于气液界面区域．气液界面的控制方程为

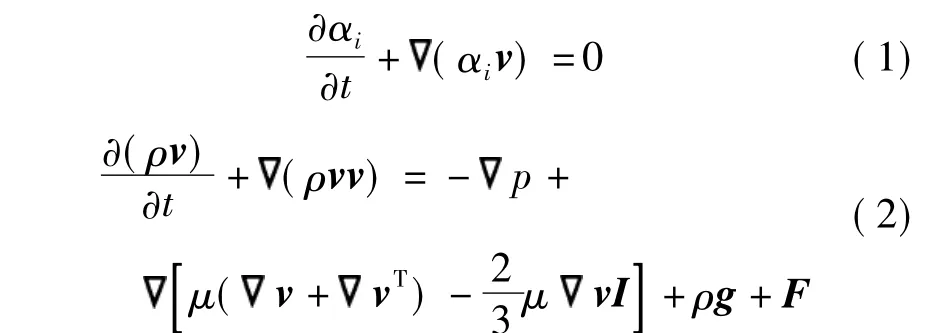
式中，F为气液界面的表面张力; p为压强; I为单位矩阵; g为重力加速度;下标i =g，l为气相和水相．

1. 2离散颗粒运动

采用DEM模型来模拟颗粒群在水相流场内的运动．单个球形颗粒在水相中的运动遵循牛顿第二定律，其运动轨迹由颗粒的作用力平衡方程来求得．颗粒在旋转流场中运动时，由于颗粒与水相间有相对运动，颗粒受到水相的拽力作用．水相中由于存在速度梯度，使得冲刷球形颗粒的力量并不均匀，且球形颗粒间的相互碰撞、摩擦或与管壁间的碰撞、摩擦等都有可能导致球形颗粒在运动过程中发生旋转．球形颗粒旋转所产生的垂直于相对速度方向的横向力，即马格努斯力．因此本文主要考虑重力、浮力、拽力和马格努斯力的作用．曳力和马格努斯力可表示为颗粒反作用于水相的作用力．

1. 3颗粒碰撞动力学

球形颗粒在扩散运动过程中，当与邻近球形颗粒的距离小于颗粒直径时，就会与邻近球形颗粒发生碰撞，碰撞过程采用软球模型［7］来描述．在该模型中，用弹簧模拟颗粒的变形，阻尼箱模拟碰撞过程中的阻尼影响，滑板模拟颗粒间的滑动摩擦力的影响．通过软球模型，不仅能够求出颗粒碰撞前和碰撞后的速度以及角速度，还能够求出碰撞过程中颗粒间的接触力．接触力分为法向接触力和切向接触力．一个球形颗粒与多个球形颗粒同时碰撞，则该球形颗粒上的接触力是该颗粒与多个球形颗粒碰撞力的合力［14］．对于颗粒和壁面之间的碰撞，计算方法与颗粒间的碰撞类似，只需将壁面看作是速度为零、直径为无穷大的颗粒．

1. 4边界条件

在如图1所示的容器内，水相和气相在固壁旋转作用下发生运动，壁面处速度边界条件为

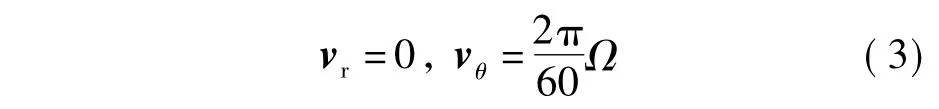
式中，vr为径向速度; vθ为切向速度;Ω为容器的转速．

2　数值求解及验证

计算过程中，采用欧拉方法对气液连续相流场进行求解;对控制方程压力项的离散采用PRESTO格式;动量方程的离散采用具有二阶精度的迎风格式;对压力与速度间的耦合计算采用隐式算子SIMPLE算法;使用显式时间离散格式求解气液界面动力学方程．在数值计算中，采用不同的网格尺寸进行了网格独立性检测，当在2个网格下颗粒浓度曲线的变化趋于一致时，表明数值解是网格独立的．

图2　数值模拟结果与实验结果比较

为验证本文所建立理论模型的正确性，图2分别给出了数值模拟得到的颗粒及速度分布与文献［11］中的实验结果．从图中可以看出，数值模拟得到的颗粒在圆筒内液相中的速度及颗粒分布与实验结果吻合较好，表明模型是合理的．

3　结果分析与讨论

3. 1流场及颗粒运动

图3给出了容器逆时针旋转时颗粒分布随时间的变化．在初始时刻，颗粒群分布在旋转容器水相底部．由图可知，当旋转容器转动时，水相在壁面剪切作用力下产生旋转流场，颗粒在该流场中运动并分散．颗粒沿旋入侧运动并分散，而后形成一个旋流型环状分布，最终分散至水相区域．分析容器内水相的流场可知，颗粒群的这个运动特性主要是由于在水相中的中心位置存在涡流场(见图4)，颗粒跟随涡流运动并逐渐分散．水相中流场受到容器旋转速度的影响，因而容器旋转速度会影响颗粒在水相中的运动和分散．

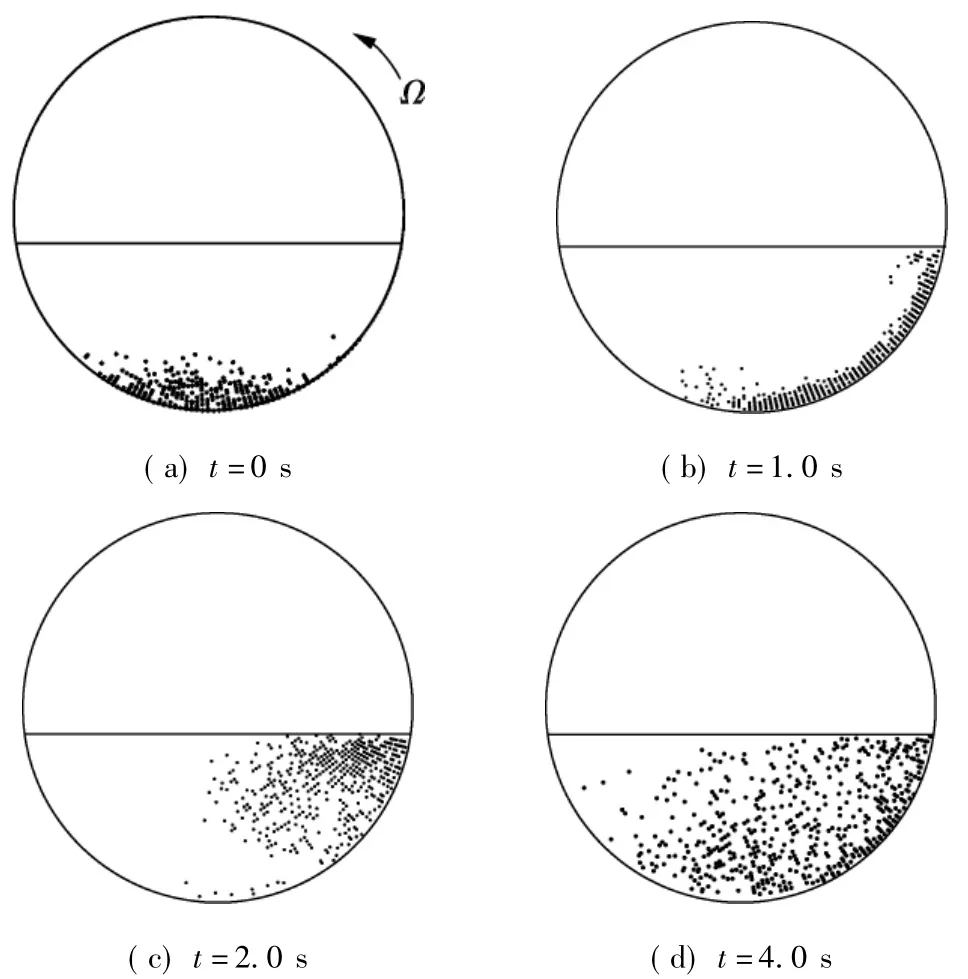
图3　颗粒分布随着时间的变化(Ω=40 r/min)

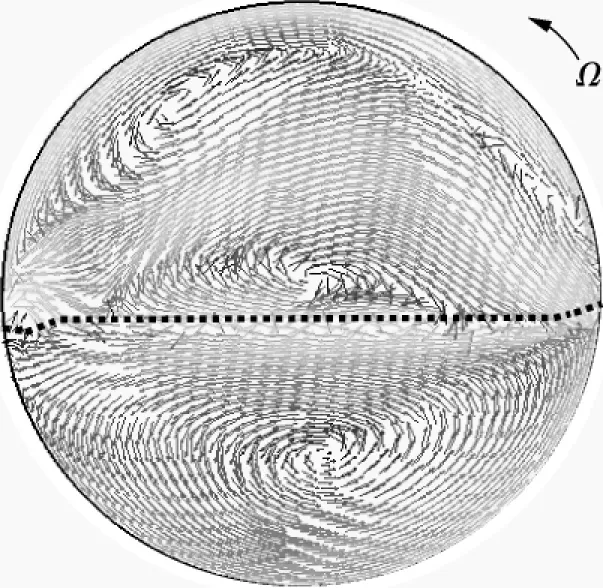
图4　气液速度分布(Ω=40 r/min)

为进一步清晰显示颗粒在水相中的运动过程，图5给出了单颗粒在水相中的运动轨迹图．由图可知，不同初始位置的颗粒在水相中有着不同的运行轨迹．每个颗粒都经历了一个环形的运动轨迹，轨迹方向变化大的地方是由于颗粒的碰撞引起的，如颗粒与壁面碰撞引起运动方向的改变(见图5(a) 和(b)中虚线框)、颗粒与颗粒碰撞引起运动方向的改变(见图5(c)中虚线框)．可见，在旋转圆筒容器内颗粒的运动轨迹受颗粒之间碰撞、颗粒与壁面之间碰撞以及水相对颗粒的作用力综合影响．在颗粒群的运动过程中，颗粒主要在水相的中心区域和旋出侧运动，很少到达旋入侧，且颗粒运动轨迹直接受水相流场的影响，颗粒围绕着旋转流场做周向运动．从以上分析可知，如果颗粒尺寸和旋转速度改变，则重力以及颗粒在外水中受到的拽力等力的大小也会发生改变，进而改变决定颗粒运动的合力，并最终影响颗粒在水相中的轨迹．

图5　颗粒运动轨迹(Ω=40 r/min)

3. 2颗粒的分散性能

为量化分析旋转容器内颗粒群在水相中的分散特性，采用分散指数D来定量评价颗粒群的分散程度，其表达式为

式中，S为水相中统计颗粒浓度值的标准方差;珋c为水相计算域内所有单元内统计颗粒浓度的平均值．分散指数D是一个描述水相中颗粒分散程度的无量纲数值．D值越小，则意味着分散程度越大．标准方差S的计算式为

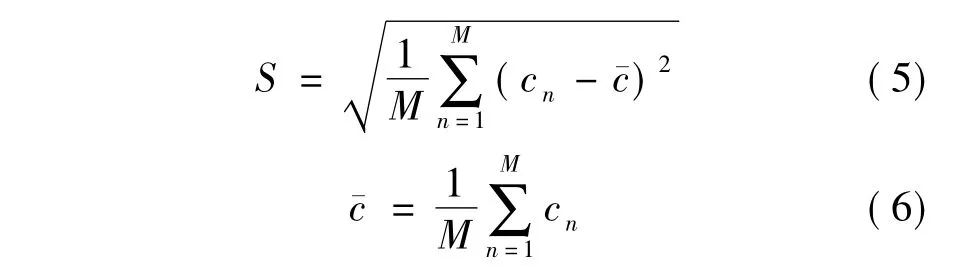
式中，M为统计单元总数; cn为第n单元的统计颗粒浓度．

3. 2. 1颗粒液体密度比对分散性能的影响

颗粒在水相中运动受到多种力的作用，重力是主要的作用力之一，而颗粒密度大小变化能改变重力的大小，从而影响颗粒在水相中的运动行为及分散性能．图6给出了Ω=60 r/min，H =44 mm，ρl=1 000 kg /m3条件下，颗粒液体密度比rd= 1. 0 ～2. 5时，旋转容器内颗粒群在水相中达到准稳态的分散指数．从图中可以看出，旋转容器内的颗粒准稳态分散指数随着颗粒液体密度比rd的增加而增加．这表明颗粒密度不匹配度的增加会导致颗粒分散驱动力的下降．这是因为在忽略颗粒碰撞的情况下，球形颗粒受力平衡时其向下重力、向上浮力的合力与液体拽力满足相等关系．随着颗粒液体密度比rd的增加，有效重力超过拽力的作用，从而成为控制颗粒运动行为的基本因素．然而拽力是驱动颗粒在水相中运动及分散的主要驱动力，因此，有效重力的增加导致了颗粒群在水相中分散性能的下降．

图6　颗粒液体密度比对分散指数的影响

3. 2. 2液体黏度对分散指数的影响

改变液体黏度可使得旋转容器内水相流场发生变化．液体黏度影响颗粒雷诺数，并进一步影响作用于颗粒上的拽力，而拽力对于旋转容器内颗粒在水相中的运动行为有着重要影响．图7给出了Ω =60 r/min，H =44 mm，rd=1. 1时，不同液体黏度条件下旋转容器内颗粒群在水相中达到准稳态时的分散指数．从图中可以看出，随着液体黏度的增加，颗粒的准稳态分散指数逐步下降．该结果表明，液体黏度的增加能够改善旋转容器内水相中颗粒的分散性能．

图7　液体黏度对分散指数的影响

4　结论

1)当容器转动时，水相在壁面剪切作用力下产生旋转流场，颗粒群随水相旋转流场中的涡流运动并逐渐分散至整个水相区域．

2)在颗粒群的运动过程中，颗粒主要在水相的中心区域和旋出侧运动，很少到达旋入侧．

3)旋转容器内颗粒群的分散指数随着颗粒液体密度比的增加而增加，即颗粒密度增加会导致颗粒分散驱动力的下降，使得颗粒群在液相中的分散性能下降．

4)随液体黏度的增加，颗粒群的分散指数逐步下降，因而液体黏度增加能够改善旋转容器内水相流场中颗粒群的分散性能．

参考文献(References)

［1］Ghanem A，Lemenand T，Valle D D，et al．Static mixers: Mechanisms，applications，and characterization methods: A review［J］．Chemical Engineering Research＆Design，2014，92 (2) : 205－228．DOI: 10. 1016/j．cherd．2013. 07. 013．

［2］Thakur R K，Vial C，Nigam K D P，et al．Static mixers in the process industries: A review［J］．Chemical Engineering Research＆Design，2003，81(7) : 787－826．DOI: 10. 1205/026387603322302968．

［3］Wadnerkar D，Utikar R P，Tade M O，et al．CFD simulation of solid-liquid stirred tanks［J］．Advanced Powder Technology，2012，23 (4) : 445－453．DOI: 10. 1016/j．apt．2012. 03. 007．

［4］Tamburini A，Cipollina A，Micale G，et al．CFD simulations of dense solid-liquid suspensions in baffled stirred tanks: prediction of solid particle distribution［J］．Chemical Engineering Journal，2013，223: 875－890．DOI: 10. 1016/j．cej．2013. 03. 048．

［5］李良超，杨军，徐斌．轻密度颗粒在搅拌槽内悬浮特性的数值模拟［J］．农业工程学报，2013，29(16) : 42－49．DOI: 10. 3969/j．issn．1002－6819. 2013. 16. 006．Li Liangchao，Yang Jun，Xu Bin．Numerical simulation of solid-liquid suspension characteristics for low-density particles in stirred vessel［J］．Transactions of the Chinese Society of Agricultural Engineering，2013，29 (16 ) : 42－49．DOI: 10. 3969/j．issn．1002－6819. 2013. 16. 006．(in Chinese)

［6］Jovanovi A，Pezo M，Pezo L，et al．DEM /CFD analysis of granular flow in static mixers［J］．Powder Technology，2014，266: 240－248．DOI: 10. 1016/j．powtec．2014．06．032．

［7］Cundall P A，Strack O D L．Discrete numerical-model for granular assemblies［J］．Géotechnique，1979，29 (1) : 47－65．DOI: 10. 1680/geot．1979. 29. 1. 47．

［8］Kafui K D，Thornton C，Adams M J．Discrete particlecontinuum fluid modelling of gas-solid fluidised beds ［J］．Chemical Engineering Science，2002，57 (13) : 2395－2410．DOI: 10. 1016/S0009－2509(02) 00140－9．

［9］Sakai M，Shigeto Y，Sun X S，et al．Lagrangian-Lagrangian modeling for a solid-liquid flow in a cylindrical tank［J］．Chemical Engineering Journal，2012，200-202: 663－672．DOI: 10. 1016/j．cej．2012. 06. 080．

［10］Sun X S，Sakai M，Yamada Y．Three-dimensional

simulation of a solid-liquid flow by the DEM-SPH method［J］．Journal of Computational Physics，2013，248: 147－176．DOI: 10. 1016/j．jcp．2013. 04. 019．［11］Sun X S，Sakai M，Sakai M T，et al．A Lagrangian-

Lagrangian coupled method for three-dimensional solidliquid flows involving free surfaces in a rotating cylindrical tank［J］．Chemical Engineering Journal，2014，246: 122－141．DOI: 10. 1016/j．cej．2014. 02. 049．［12］Zhang J，Yong L，Fan L S．Discrete phase simulation of gas-liquid-solid fluidization systems: Single bubble rising behavior［J］．Powder Technology，2000，113 (3) : 310－326．DOI: 10. 1016/S0032－5910 (00) 00314－4．

［13］Brackbill J U，Kothe D B，Zemach C．A continuum method for modeling surface tension［J］．Journal of Computational Physics，1992，100 (2) : 335－354．DOI: 10. 1016/0021－9991(92) 90240－Y．

［14］Crowe C，Schwarzkopf J D，Sommerfeld M，et al．Multiphase flows with droplets and particles［M］．2nd ed．New York: Taylor＆Francis Group，2012: 119－153．

Motion characteristics of particle swarm in rotational flow field

Chen Yunfu Zhang Chengbin Chen Yongping
(Key Laboratory of Energy Thermal Conversation and Control of Ministry of Education，Southeast University，Nanjing 210096，China) (School of Energy and Environment，Southeast University，Nanjing 210096，China)

Abstract:An nonstationary theoretical motion model of the particle swarm motion in the water phase in a partly filled rotating container is proposed．Numerical analyses are performed to investigate the motion characteristics of particle swarm in rotational flow field．The influences of flow fields，the evolution of the particle swarm，motion trajectories as well as the liquid viscosity and the particle density on the dispersion performance of the particle swarm are analyzed．A comparison of the particle and velocity distribution between simulation results and experimental data in literature is carried out to valid the proposed mathematical model．The results indicate that the vortex occurs in the water phase，in which the particle swarm move following the vortex and gradually disperse into the whole region of the water phase．The distribution of the particle swarm in the water phase become more uniform with the increase of the liquid viscosity．The driving force of particle dispersion declines with the increase of the particle density．Finally the particle swarm accumulates at the region where the container rotates out the water phase．

Key words:particle; VOF-DEM(volume of fluid-discrete element method) ; rotational flow field; dispersion

基金项目:国家自然科学基金NSAF联合基金资助项目(U1530260)、国家自然科学基金资助项目(51306033)、江苏省自然科学基金资助项目(BK20130621)．

收稿日期:2015-08-03．

作者简介:陈云富(1979—)，男，博士生;陈永平(联系人)，男，博士，教授，博士生导师，ypchen@ seu．edu．cn．

DOI:10．3969/j．issn．1001－0505．2016．01．013

中图分类号:TL632

文献标志码:A

文章编号:1001－0505(2016) 01-0076-05