渐行渐悟渐悟渐深
——罗鸣亮老师《长方形的面积》教学赏析
周爱芳
罗老师每次的课总留给听课老师深刻的印象:简约的素材,独特的教具,风趣亲切的言语,蹲下来和学生友爱的交流,睿智大气的设计……让我们走进罗老师的《长方形的面积》,去深刻领会他和学生们的又一次精彩:
一、复习引入,猜疑感悟
师:罗老师从福建带来了一个信封,里面躲着图形。猜对了,就是你下午的礼物!第一个图形,它的面积是1平方分米,这个图形是?
生:正方形。
师:同意吗?(出示正方形)猜对了,送给你!这个正方形的边长是?
生:1分米。
师:很棒!第二个图形,它的面积是3平方分米,它是?
生:它是长方形。
师:(追问)你是怎么想的?
生:3平方分米,3个正方形拼在一起可以拼成一个长方形。
师:我们一起来看看她猜对了没有。
师:猜对了吗?
生:不对。
师:(追问)我说这个图形它的面积是3平方分米说的对不对?你是怎么看出来面积是3平方分米的?
生:这个图形由3个面积是1平方分米的正方形组成,所以这个图形的面积是3平方分米。
师:刚才那位同学猜对了没有?(没有)你们为什么想到的都是长方形呀?
生:我们见到最平常的一般都是长方形,忽略了别的不规则图形,所以这是一个漏洞。
师:说得真好,掌声送给她!知道了这是一个漏洞,你们想到的都是规则的长方形,正方形,我们就从规则的长方形、正方形开始研究……
【赏析:学习“长方形的面积”是学习“面积与面积单位”的延续。罗老师准确地把握住学生的真实起点,用诙谐幽默的话语吸引学生,首先让学生猜1平方分米的图形,学生不知不觉地回忆起边长是1分米的正方形面积是1平方分米这一旧知。接着让学生继续猜面积是3平方分米的图形,当学生都猜是长方形时,罗老师却出示了一个不规则图形,目的在于防止学生思维定势,让学生从“规则化”浅显的认知走向数学的本质,从中感悟不管是什么图形,相同单位面积累加得到的总面积都是相同的,如果再增加一个,总面积就随着增加一个单位面积。同时又让学生隐约感悟到平面图形的面积指的是封闭图形的大小,它的面积都可以用单位面积去测量,不受它的形状、边线影响,这种深远的思考既为下面的教学环节做了铺垫,也为学生后续学习面积与周长概念的区分做好了铺垫。】
二、层层展开,说理渐悟
师:它是由6个面积是1平方分米的正方形拼成的长方形,它会是什么样子的呢?
生:上面有3个1平方分米的正方形,下面也有3个。
教师引导:他说的有几行?每行摆几个?总共摆了几个?
生:摆2行,每行3个,总共摆了6个。
师:6个什么?它的面积就是?
生:6个1平方分米的正方形,面积是6平方分米。
生2:我认为还有一种,摆1行,每行6个,一共摆了6个,面积也是6平方分米。
师:为什么也是6平方分米呀?
生:因为有6个1平方分米的正方形。
……
课件出示:

师:看谁最快知道它的面积?知道的请举手。
生:12平方分米。
教师:讲道理,你会讲道理吗?
生:因为有3行,每行4个,一共12个。
师:(追问)12个什么?所以它的面积就是?
课件出示

师:面积是多少?
生:24平方分米,因为每行4个,有6行,一共有24个1平方分米的小正方形。(掌声送给会讲道理的同学!)
……
课件出示:
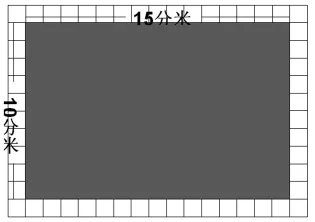
师:你那么快想出来了,猜猜为什么她还没想出来?
生:她可能还在数,其实不用数,每行15个,有10行,乘起来就知道有150个了。
师:图中写着的是15分米呀,怎么就知道每行15个?
生:长方形边是15分米,1个小正方形是1分米,那就可以摆15个。
教师演示课件:第一行摆15个(一个一个摆)。
师:如果有30分米呢?每行可以摆几个?你又怎么知道有10行?
生:有10分米,1个小正方形是1分米,竖着就有10个小正方形,就有10行。
教师演示课件:第一列摆10个(一个一个摆)。
师:那就说明一共可以摆几个?面积是多少?
……
【赏析:在这一环节探究6平方分米的长方形时,罗老师一改以往告知长和宽求面积的做法,也没有要求或询问学生怎么拼摆,而是继续让学生去猜是怎样的长方形,这种新颖的设计激发了学生主动地在脑海中用1平方分米去拼摆,发展学生的空间想象力。更令人叹为观止的是,在教学6平方分米、12平方分米、24平方分米、36平方分米时……罗老师都是让学生充分地“讲道理”:每行有几个?有几行?一共有几个1平方分米的小正方形,面积总共是多少平方分米?由长方形到正方形,再到更大的长方形,借助方格图,不断增加数量,从已知面积猜图形到根据图形猜面积等,使学生慢慢地领悟到长方形的面积就是看每行摆几个单位面积,有几行,算出总个数,总个数是几面积就是多少。到150平方分米更大的长方形时,罗老师紧紧追问学生:图中写着的是15分米呀,怎么知道每行有15个?又怎么知道有10行?让学生自主地去联系长方形的长和宽,进一步让学生弄清每行摆单位面积的个数与长方形“长”的单位长度个数之间的相等关系,以及可以摆的行数与长方形“宽”的单位长度个数之间的相等关系,顺着学生的思维,逐步地引导学生渐渐去感悟长方形的面积=长×宽。】
三、步步深入,渐悟渐深
师:信封里的这个长方形你能算出它的面积,就是你的礼物了。 (出示一个长方形),什么都没告诉你,有办法算出它的面积吗?
学生独立计算这个长方形的面积后反馈。
师:你又做了什么事情?
生:长方形的长有5厘米,宽有4厘米,5×4=20(平方厘米)。
师:我要你们去计算它的面积,你干吗要去量它的长和宽?
生:它的长是5厘米,所以用1平方厘米的小正方形可以摆5个,它的宽是4厘米,用同样的小正方形可以摆4个。所以5×4=20,就可以摆20个小正方形。
师:20个什么样的小正方形?
生:1平方厘米的小正方形,所以是20平方厘米。
师:道理讲得太好了,掌声送给他!
师:罗老师家里也有一个长方形,面积一样(20平方厘米),但形状不一样,猜猜看我家那个长方形的长和宽可能分别是?
生:长是20厘米,宽是1厘米。
师:你是怎么想的?(长是20厘米,宽是1厘米,面积就是20平方厘米)你怎么知道面积是20平方厘米?
生:摆一行,一行20个。
生:还可以长是10厘米,宽是2厘米。
教师出示课件:

师:我家的长方形很苗条,你觉得是哪个?为什么?我家的长方形的长有可能比20厘米还长吗?
生:不能,长已经是20平方厘米,是极限了。
生:能的,只要宽改成0.5厘米,长改成40厘米。(教师课件演示)
师:我家长方形的长有可能比40厘米还长吗?
生:有可能,只要把宽分1毫米,长就会很长。
师:那我家长方形的长会有多长?
生:把宽分下去,长可以很长很长,无法计算。
……
师:学到这里,你有什么收获吗?如果让你讲一句话,你会讲什么?
生:长方形的面积=长×宽。
师:你觉得有道理吗?有什么道理?
……
【赏析:在逐渐形成长方形的面积计算方法后,罗老师直接出示一个“光秃秃”的长方形(长是5厘米,宽是4厘米未知,也没有借助方格图),让学生计算它的面积。这看似一道用来检验学生对长方形面积掌握情况的简单练习,却很好地展露了学生的思维。即使罗老师没有给予任何信息,由于前面充分的感触,学生能自己积极主动地进行思考,马上意识到长方形面积与长和宽有关,要想知道长方形面积就得先知道它的长和宽。罗老师却提出质疑:要计算的是长方形面积,干吗去量它的长和宽呢?让学生再一次进行解释,使学生对长方形面积的认识逐步走向深刻,把“每排面积单位个数、排数”与“长、宽”之间建立起对应关系。在计算面积时,只要用“单位个数”相乘,也就是长和宽相乘,就能求出一共有多少个单位面积。同时罗老师又进行巧妙的变式,猜面积是20平方厘米的长方形还可以是怎样的形状,长可以是几?宽是几?不时地逼问,让学生感悟到面积相等的不同形状长方形,宽越短,长越长,多次的等积变形再一次强化对“长方形的面积=长×宽”的理解。最后学生水到渠成地总结出长方形的面积计算方法,彻底领悟为什么长方形的面积要“长×宽”。】
四、拓展延伸,渐悟渐远
教师:信封里还剩下一个长方形,每行有4个,有2行。这个长方形的面积是?
生:8平方分米。
生:8平方厘米。
生:单位很多,但是8这个数字是确定的。
教师揭晓答案,迅速掏出长方形(学生猜测错误)。
师:问题出在哪呢?
生:问题出在它的边上,边长是5厘米的。
师:它的面积又是多少呢?
生:它的面积是200平方厘米。
师:同意吗?讲道理。
生:1个小正方形的面积是5×5=25(平方厘米),这个长方形有8个这样的小正方形,所以用25×8=200(平方厘米)。
生2:这个还可以说2平方分米,因为它们的进率是100,它是200平方厘米,可以转化为2平方分米。
师:他转化的究竟对不对呢?没关系,这是下节课的内容。
【赏析:在最后环节,罗老师还是用信封里神秘的图形将课堂推向高潮,仅仅是一个简单的问题:这个长方形每行有4个,有2行,它的面积是多少?学生振振有词,认为能想到8平方分米和8平方厘米,再加上“8这个数字是确定的”一句,已经是很完整的答案。因为整节课围绕着面积是1平方分米、1平方厘米的正方形这样单位面积展开,学生已刻骨铭心。哪知罗老师“幽”了学生一招,出示一个不是单位面积的正方形引发冲突,激励着学生更深地思考。学生们“上当”了,听课的老师也被“骗”了。然而,长方形面积应该是几?该怎样计算呢?学生恍然大悟:先计算边长为5厘米的小正方形的面积,把25平方厘米的正方形看作“单位面积”,这个长方形有8个这样的正方形,所以面积是200平方厘米,学生已悟得很深、很远了。当有学生再一次提出这个长方形面积也可以是2平方分米时,罗老师尊重学生,让他讲道理并适时抓住契机,与下节课内容“面积单位之间的进率”进行沟通联系。将课堂拓展延伸,把学生的思绪带往更深更远处……】

