混合流体岩石介电常数的CRI模型与Maxwell-Garnett模型研究

潘保芝, 栗猛, 张瑞

(吉林大学地球探测科学与技术学院, 吉林 长春 130026)

0 引 言

尽管EPT、DPT测井在20世纪70年代就推出了,由于仪器数据采集质量和精度的限制、介电频散带来的解释困难以及核磁共振测井仪器的发展使得早期的介电测井未得到充分推广。斯伦贝谢公司的多频介电频散测井仪器工作在20 MHz～1 GHz的4个频率,在碳酸盐岩结构分析、重油流动性评价、变矿化度或低矿化度地层评价等方面取得不错的应用效果[1]。中国在逐步应用这种仪器,需要深刻理解仪器原理和解释模型、方法,但研究资料较少。

不含水岩石的介电特性较为简单,极化类型主要是位移极化,介电常数取决于矿物成分和含量且与测量频率无关。地层介电特性研究的难点是混合流体岩石的介电性质复杂引起的,水溶液的存在使得岩石的极化变得复杂,同时存在界面极化、电化学极化、转向极化和位移极化。国外对多相岩石介电模型做了很多研究,如Clausisus-Mossotti混合模型、Maxwell-Garnett(M-G)模型、Polder-van Santen模型等[2],中国多是借鉴国外的研究成果或采用地区经验公式。对于水的介电模型,Gadani D H详细比较了Klein-Swift模型和Stogryn模型的计算值与实验数据的差异[3],2种模型都很符合实验数据,都可以计算水溶液的介电常数,但Stogryn模型适用的矿化度范围更大。尽管提出的混合流体岩石介电常数模型有很多,模型计算结果与实验数据的符合程度各不相同。斯伦贝谢公司进行了大量岩石物理研究,最终选择了CRI模型和M-G模型作为解释模型。本文研究了新一代介电测井仪器采用的的解释模型,对水溶液介电模型的选择了采用矿化度范围比较大的Stogryn模型,研究了25 ℃时20 MHz～1 GHz频率下比表面、矿化度、饱和度对饱和流体岩石介电常数的影响及模型的适用范围。计算模型时未考虑泥质对岩石介电常数的影响。将2种模型计算结果与前人岩石介电实验数据对比,验证了CRI模型和M-G模型的合理性。中国对岩石M-G模型的研究应用较少,本文对于多频介电测井的研究工作和实验室岩石介电常数研究具有一定参考价值。

1 水溶液介电常数的计算模型

水溶液复介电常数εw由Debye方程给出

(1)

ε0=ε0(T,0)a(N)

τ=τ(T,0)b(N,T)

(2)

式中,N是当量浓度;T是温度;其中各系数如下

a(N)=1.000-0.2551N+5.151×10-2N2-

6.889×10-3N3

b(N,T)=0.1463×10-2NT+1.000-

0.04896N-0.02967N2+5.644×10-3N3

ε0(T,0)=87.74-0.40008T+9.398×10-4T2+

1.410×10-6T3

τ(T,0)=(1.1109×10-10-3.824×10-12T+

6.938×10-14T2-5.096×10-16T3)/(2π)

(3)

当量浓度N与矿化度K的关系

N=K(1.707×10-2+1.205×10-5K+
4.058×10-9K2),0≤K≤260

(4)

式中,矿化度K单位为mg/L。对于NaCl溶液,σw有

σw=σw(25,N)[1.000-1.962×10-2Δ+

8.08×10-5Δ2-(3.020×10-5+3.92×10-5Δ)+

N(1.721×10-5-6.584×10-6Δ)]

Δ=25-T

σw(25,N)=N(10.394-2.3776N+0.68258N2-
0.13538N3+1.0086×10-2N4)

(5)

图1是Stogryn模型NaCl溶液介电常数与测量频率关系图,T=25 ℃。在1 GHz以下,水溶液的介电常数几乎不变,不存在频散现象,水溶液的介电常数一般介于50～80,远大于其他介质,这是转向极化导致的,只有在几GHz之后转向极化才跟不上测量电磁场频率的变化,溶液的介电常数变小。

图2是Stogryn模型1 GHz计算的NaCl溶液介电常数与矿化度的关系。矿化度越大,溶液的介电常数越小。这是由于溶液离子浓度增大,阻碍了水分子转向极化。由分子热运动,温度越高,水分子转向极化越弱。本文计算都取T=25 ℃。

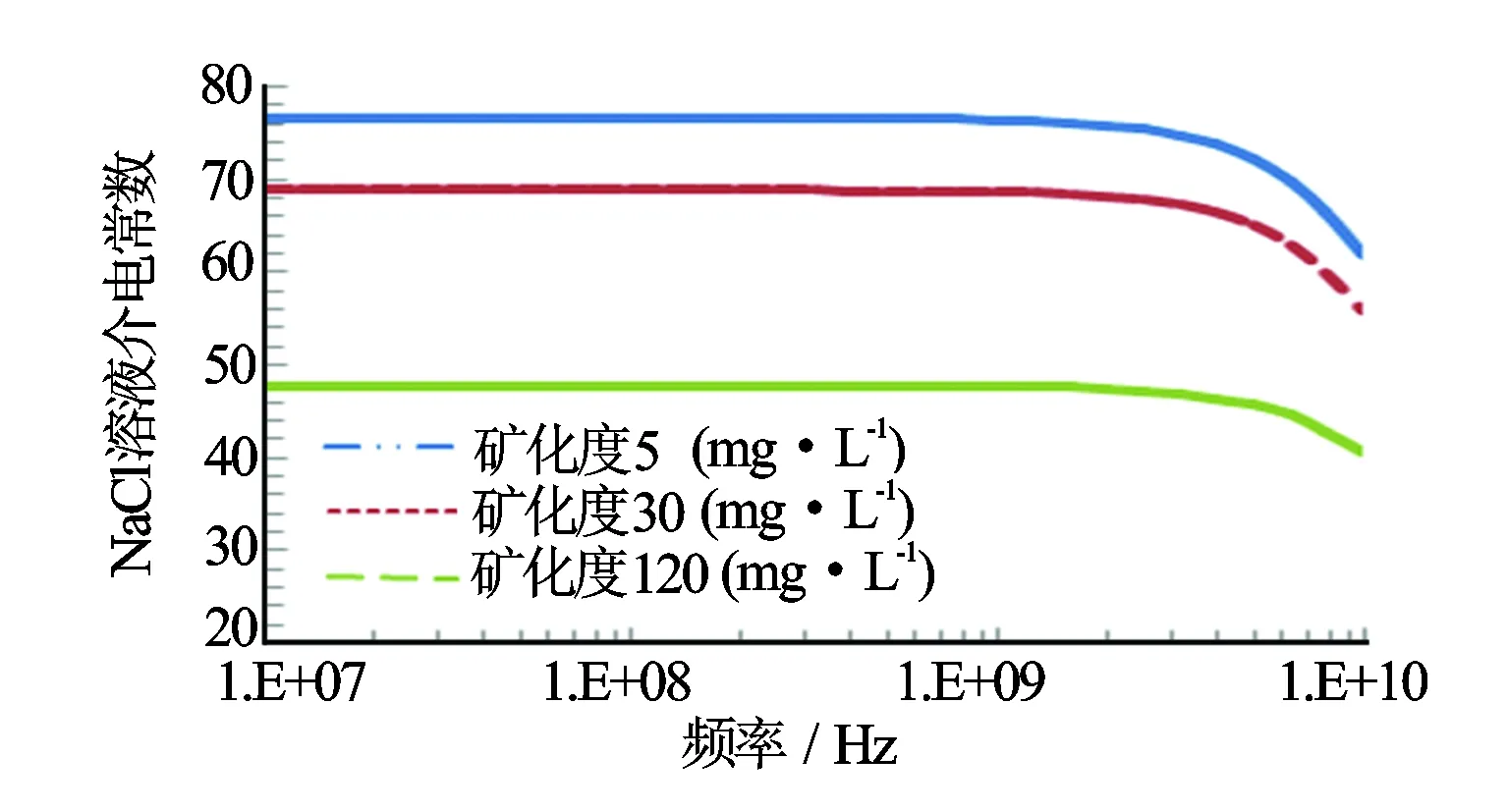
图1 NaCl溶液介电常数与频率关系图

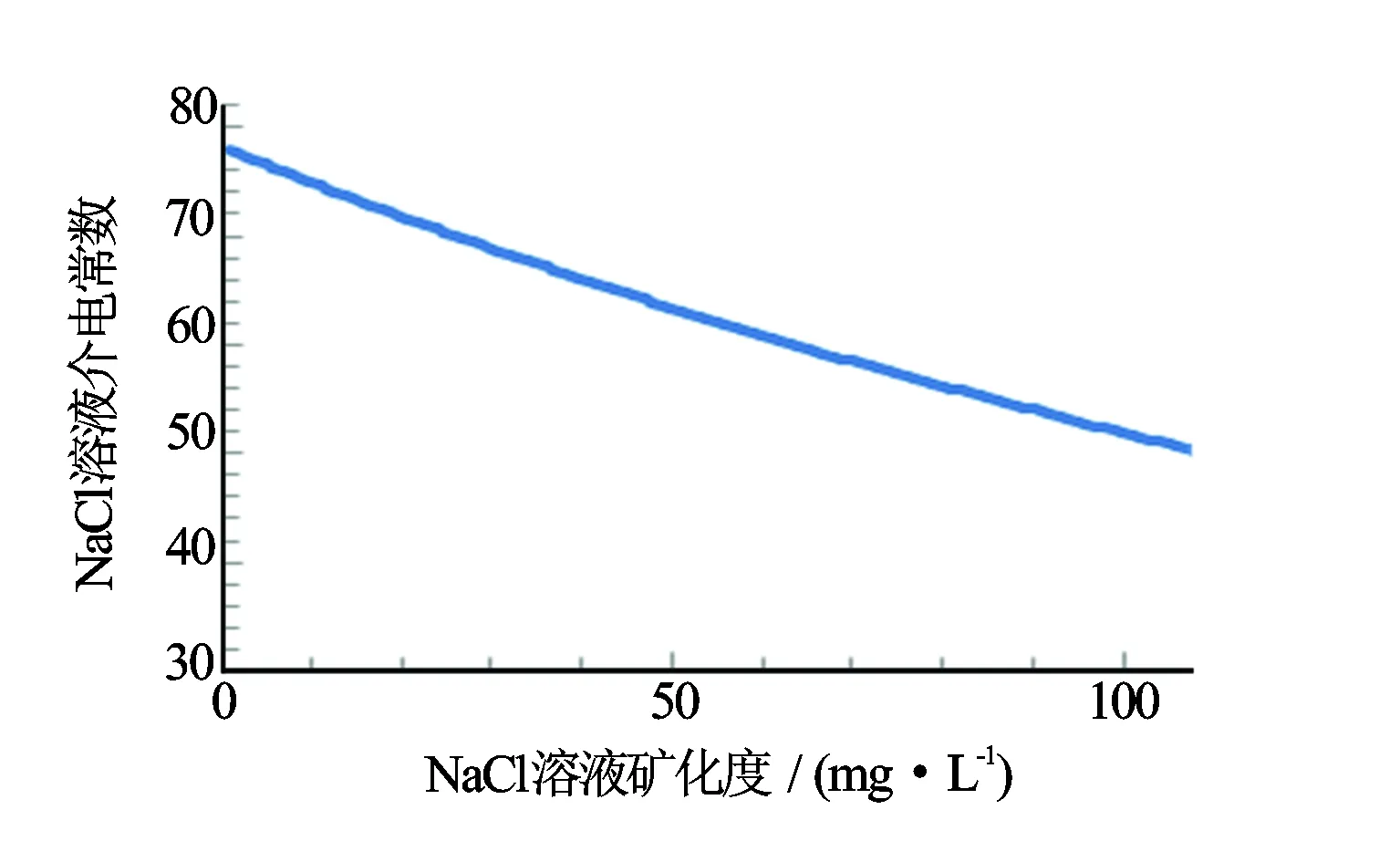
图2 NaCl溶液1 GHz下介电常数与矿化度的关系

2 CRI模型与Maxwell-Garnett模型

2.1 CRI模型

不同于水溶液和干岩样的介电常数,混合水溶液流体岩石的介电特性复杂。在MHz～GHz频段内有转向极化、界面极化、位移极化作用存在,而转向极化一般在200 MHz以上就很弱了。

对于混合水溶液流体岩石的有效介电常数,有一系列随m值变化的混合模型。

(6)

式中,fj是j相介质体积含量;εj是j相介质介电常数;m取1即是体积模型,m取2即是CRI模型。CRI模型是基于麦克斯韦方程组推导的,在MHz～GHz频段都适用,是常用的计算岩石介电特性的方法。当岩石含混合油水两相流体时,对应的饱和流体岩石介电常数的计算公式为

(7)

式中,φ为孔隙度;εm、εw、εoil分别为骨架、水、油的介电常数;Sw为含水饱和度。

2.2 Maxwell-Garnett模型

CRI模型未考虑岩石结构的影响,M-G模型考虑了饱和流体以及岩石颗粒系统中结构的影响。该模型适用于计算多相介质的介电常数,把不同的相都看作是椭球颗粒,其特点是假设介质是电动力学上的各向同性;混合物参数与电磁场强度无关;颗粒尺寸小于有效介质内的波长;参数不随时间而变化;各相物质均是随机取向椭球体等[4]。其计算公式为

εeff=εcri+

(8)

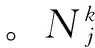
岩石复介电常数分为实部和虚部,虚部对应电导率信息,有

(9)

式中,ε′、ε″、σ分别为岩石介电常数的实部、虚部和电导率,本文主要研究了岩石介电常数的实部。退极化因子的计算方法如下。

为简化模型,选取旋转椭球体作为颗粒模型,对于j相旋转椭球体,设3个轴长分别为a、b、c,b=c,a为短轴。各方向退极化因子之和为1,则有

(10)

令b/a=q,q>1,代表轴比[6]。则有

(11)

图3是颗粒各方向退极化因子大小与q值的关系。对于常见骨架q值一般介于1～30,a轴退极化因子在0.33～1之间迅速变化,可见颗粒轴比对退极化因子影响明显。

骨架比表面为

(12)

对于石英砂岩骨架,颗粒密度取ρ=2.65 g/cm3。图4是骨架颗粒比表面与q值的关系,结果表明M-G模型的骨架比表面与颗粒长轴长度成反比,与轴比近似成正比。

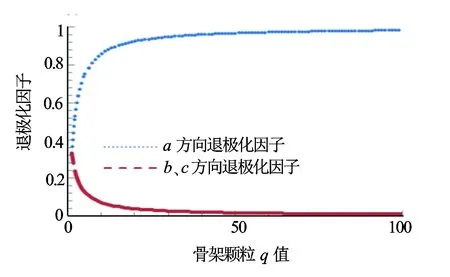
图3 骨架颗粒各方向退极化因子大小与q值的关系

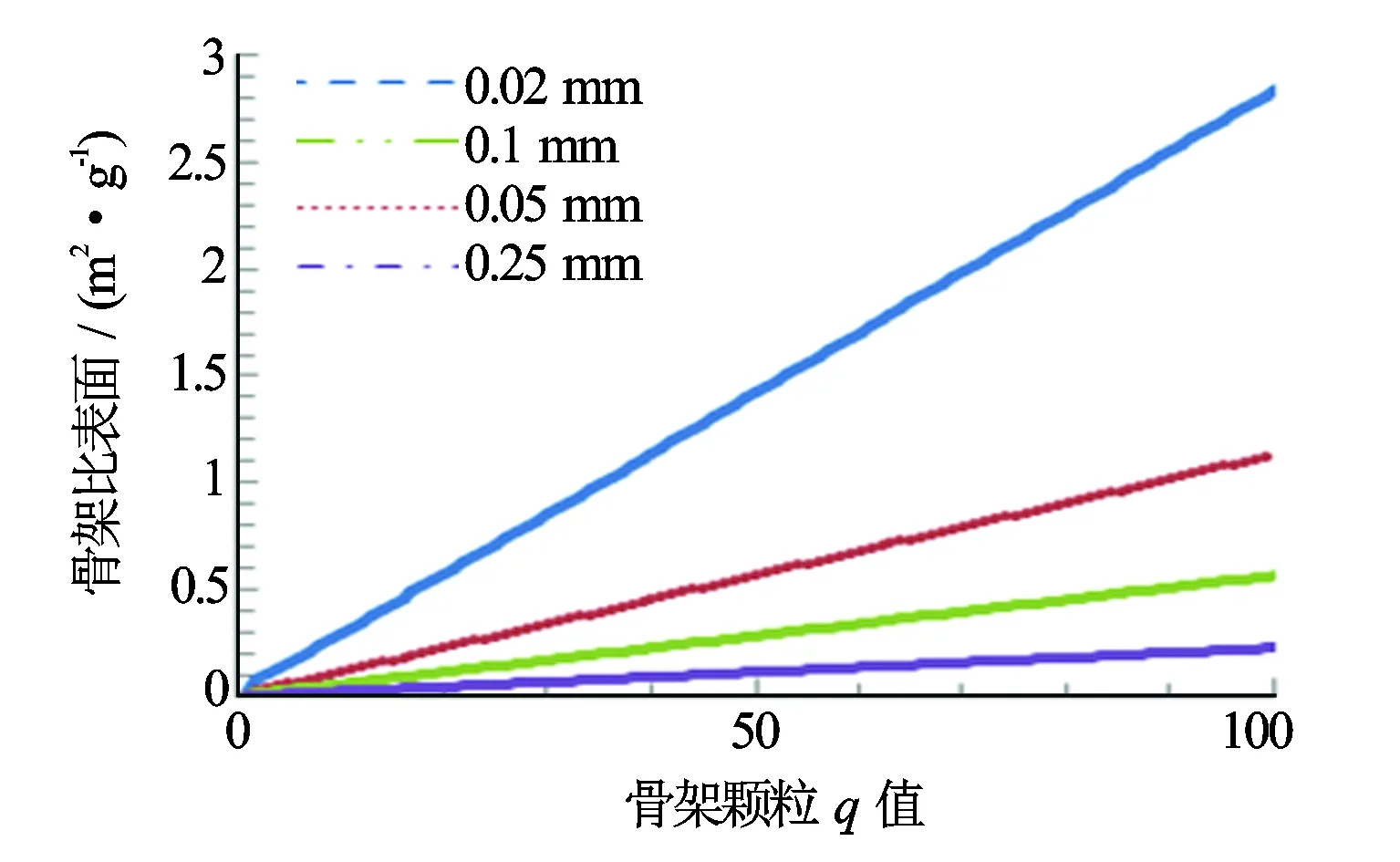
图4 不同轴长骨架颗粒比表面与q值的关系

2.3 2种模型的比较

砂岩骨架和油的介电常数分别取4.65、2。图5是孔隙度30%、含水饱和度100%、矿化度0.3%、水的q取10时CRI模型与不同骨架q值的M-G模型和频率的关系。图6是M-G模型中水的q值取10的情况下矿化度0.30%、孔隙度30%、含水饱和度100%时改变骨架q值的4种频率下的计算结果。

图5中M-G模型不同q值曲线在低频高频两端的交会和图6在20 MHz频率以下的异常结果表明M-G模型只适合几十MHz以上的测量频段。高q值对应更加扁平的颗粒,有着高的比表面,液体与骨架颗粒作用面积越大,结构影响越强,界面极化越强,介电常数越大,可以看作是由一个个小的平行板电容器造成介电常数的增大。在1 GHz处,M-G模型和CRI模型计算结果差别不大,说明此时结构几乎不起作用。

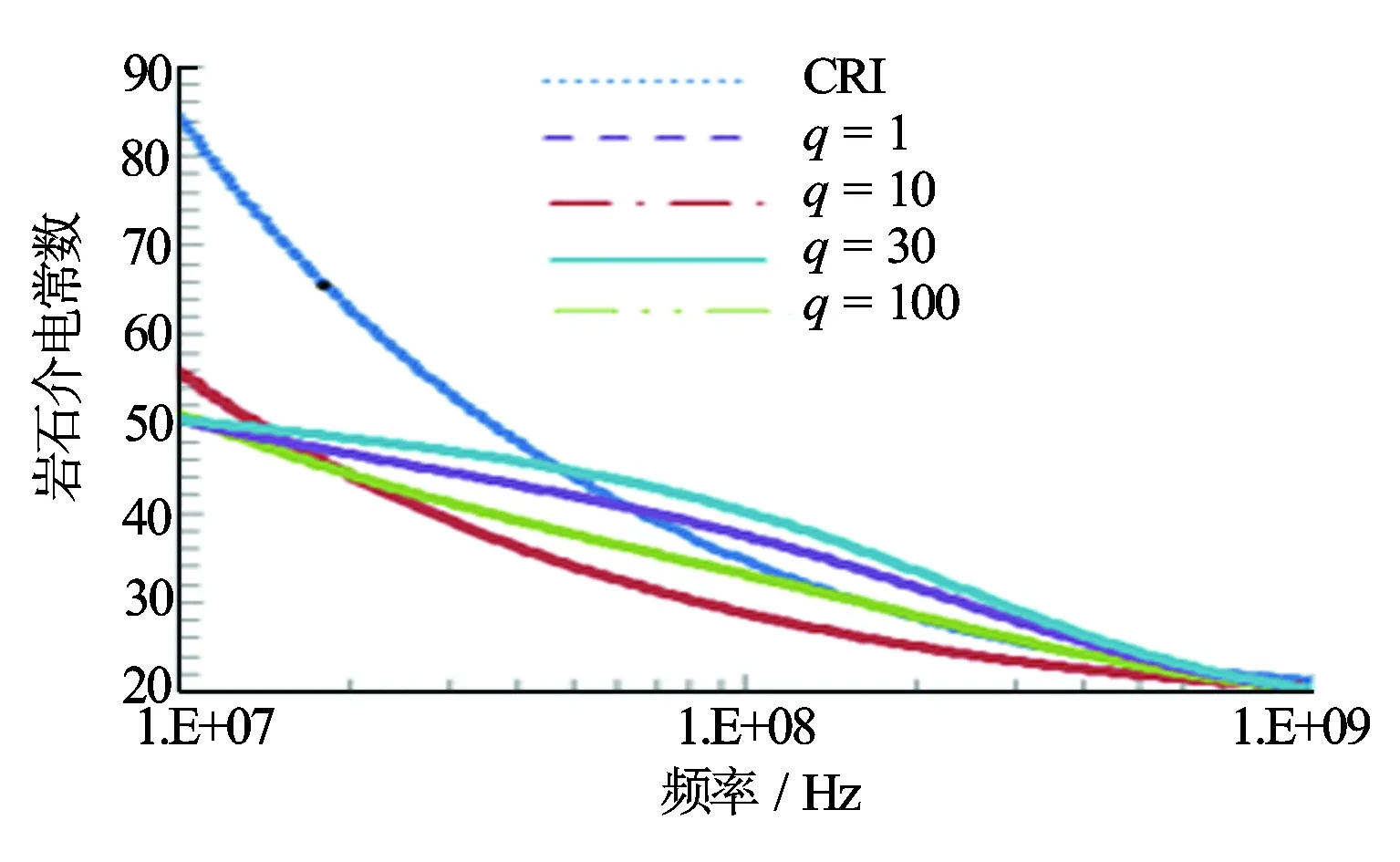
图5 不同q值的M-G模型与CRI模型与频率的关系

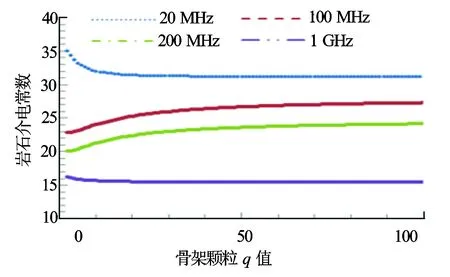
图6 不同频率下M-G模型介电常数与骨架q值的关系

图7是改变溶液矿化度对岩石介电常数的影响。可以看出,频率的影响很大。20 MHz时2种模型的计算结果相差较大,CRI模型的计算结果远大于M-G模型。200 MHz以上,2种模型相差很小。矿化度越高,2种模型的介电常数越大,且CRI模型受其影响更明显。1 GHz时矿化度对2种模型得影响都很小。但矿化度非常大的话,影响依然不可忽略。

上述结果看出,1 GHz频率下结构、矿化度的影响都很弱,这也是早期EPT测井选择1.1 GHz的测量频率的原因,当时的测量信号主要反映的是含水体积。

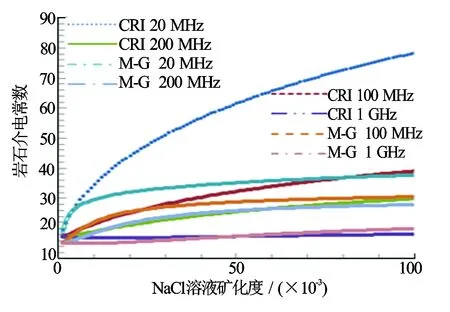
图7 CRI、M-G模型与NaCl溶液矿化度的关系

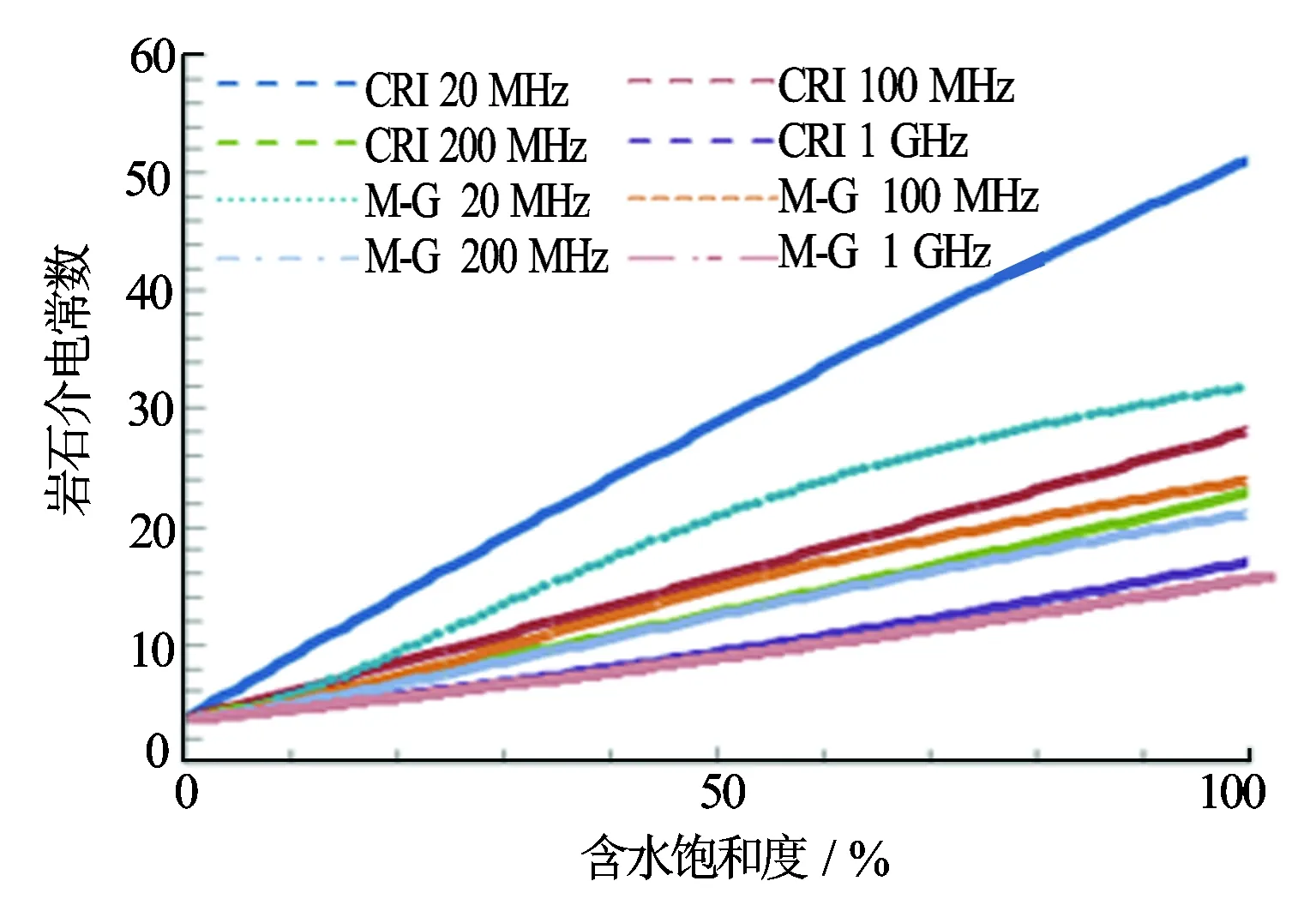
图8 CRI、M-G模型与含水饱和度的关系

图8是改变含水饱和度2种模型的计算结果。CRI模型随含水饱和度近似于线性增加,M-G模型在200 MHz以上也是近似线性增大的。200 MHz以下介电常数随含水饱和度而增大的速率先快后慢。事实上,这是由于开始增加的水与颗粒接触密切,存在的界面极化使得介电常数增大速率快,后来增大的水的体积主要是自由水,介电常数增大速率就慢了。而且,界面极化受频率影响很大,频率越高,界面极化越弱,200 MHz以上就很微弱了。至于孔隙度对岩石介电常数的影响,就是岩石介电常数受含水体积的影响。

3 与前人实验结果对比

根据唐炼、张守谦等和唐炼、韩有信等的研究[7-8],1.1 GHz频率下岩石的介电常数随矿化度变化很小。矿化度增加时,介电常数的增大幅度与频率有关,频率越高,增大幅度越小。验证了2种模型矿化度的计算结果。图9、图10分别是唐炼等实验测量数据与本文计算结果,石英骨架取4.65。计算结果与测量结果符合较好,相差一般在一个单位之内。

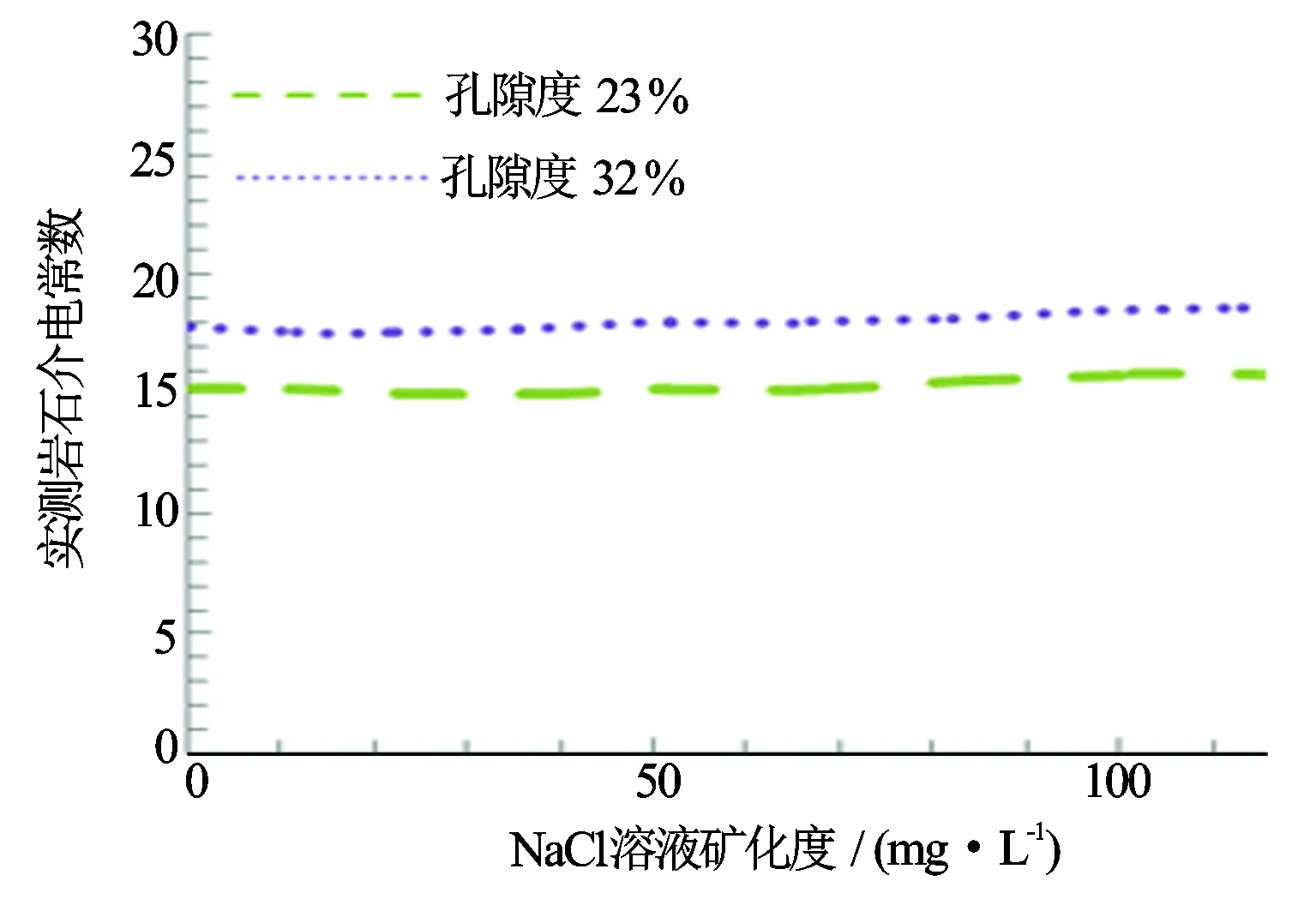
图9 实测岩样介电常数与矿化度的关系[8]

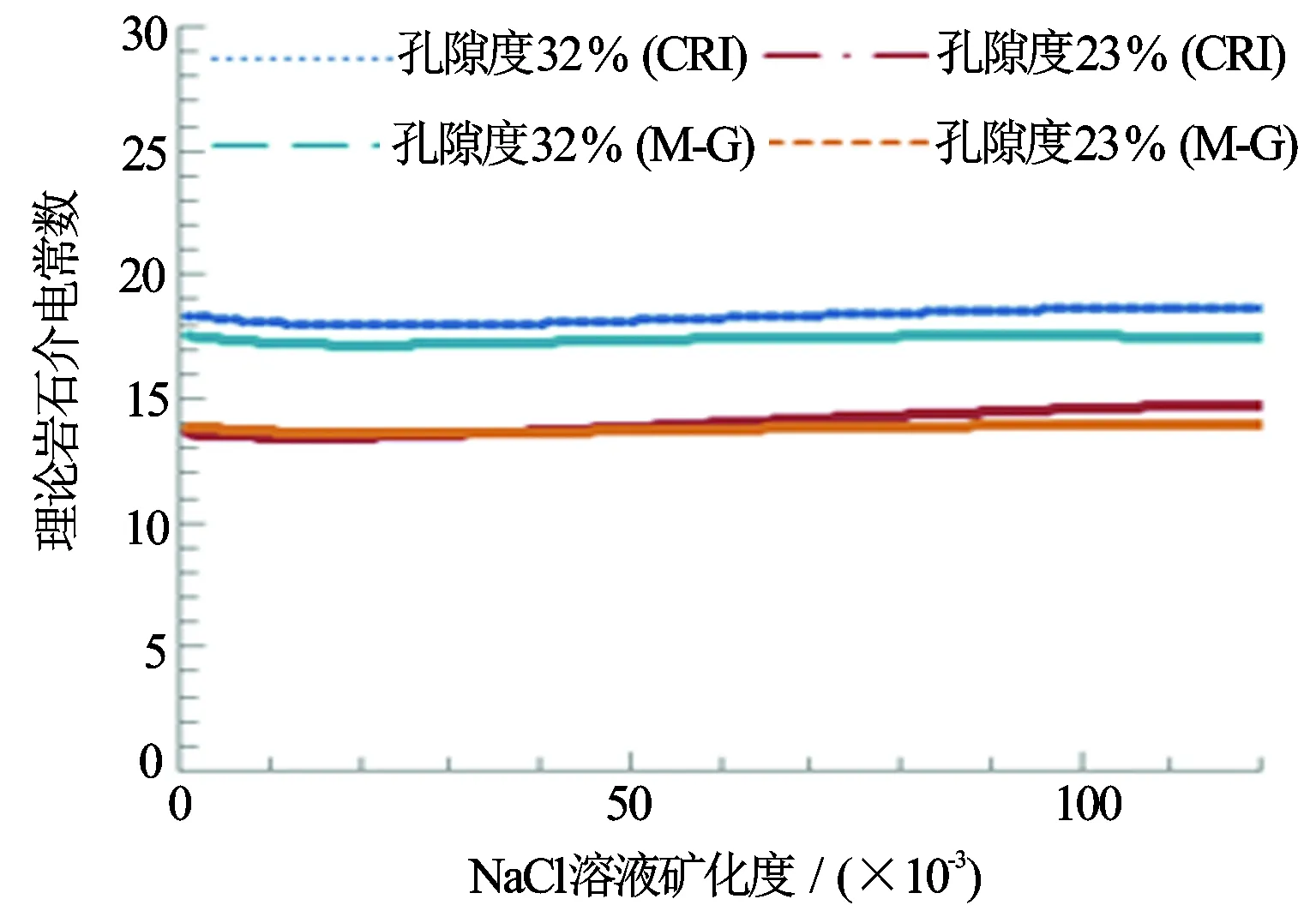
图10 理论计算岩样介电常数与矿化度的关系

根据高卫国、谢然红的实验研究[9],47 MHz频率时岩石介电常数随含水饱和度而增大的速率大于200 MHz的情况,47 MHz时岩石介电常数随含水饱和度增大速率先快后慢,200 MHz则近似线性增大,符合M-G模型介电常数随含水饱和度变化的计算结果;47 MHz受矿化度影响大于200 MHz,且岩样比表面越大,介电常数越大,测量频率越高,比表面的影响越低,这都与本文计算符合,对47 MHz和200 MHz条件下岩石介电常数随含水饱和度的变化规律的差异解释为水分子转向极化和界面极化作用强弱的影响,200 MHz以上主要是转向极化的作用,47 MHz时2种作用都影响。

冯启宁、李晓明等[10]的实验也发现,随含水饱和度的增加,介电常数增高,含水饱和度达到某一特定值后,介电常数的变化趋于平缓,并且特定值和岩性与比表面有关。这与计算结果吻合。

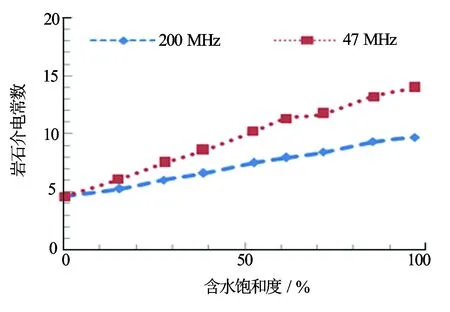
图11 岩样介电常数与含水饱和度的关系[9]

前人实验结果与理论模型的计算结果符合很好,说明应用这2种模型计算岩石介电常数与各种因素的关系很适合。CRI模型是M-G模型的基础,在频率较低(200 MHz以下)采用M-G模型符合实际情况,频率较高时2种模型差别不大。

4 结 论

(1) 采用Stogryn模型计算水的介电常数矿化度适用范围大,水的介电常数取决于温度、矿化度、测量频率,但1 GHz以下无频散,其值一般介于50～80。

(2) 20 MHz～1 GHz下含水饱和度、矿化度、孔隙度、颗粒轴比增大都会使岩石介电常数增大且测量频率越高,水的影响越突出,其他因素的影响越弱,1 GHz频率时基本只和含水量有关。岩石在200 MHz以下介电常数随含水饱和度增大而增大的速率先快后慢是界面极化作用导致的。

(3) CRI模型与Maxwell-Garnett模型计算结果在200 MHz以上差别不大,在200 MHz以下,两者计算结果差异较大,这是结构的作用导致的。且频率越低,结构的影响越大,且Maxwell-Garnett模型有一定频率适用范围。

参考文献:

[1] Romulo Carmona, Eric Decoster, Jim Hemingway, et al. 介电测井新技术与应用 [J]. 国外测井技术, 2013(5): 62-74.

[2] Seleznev N, Boyd A, Habashy T, et al. Dielectric Mixing Laws for Fully and Partially Saturated Carbonate Rocks [C]∥SPWLA 45th Annual Logging Symposium, June 6-9, 2004.

[3] Gadani D H, Rana V A, Bhatnagar S P. Effect of Salinity on the Dielectric Properties of Water [J]. Indian Journal of Ure&Applied Physics, 2012(50): 405-410.

[4] Koledintseva M Y, Du Broff R E, Schwartz R W. A Maxwell-Garnett Model for Dielectric Mixtures Containing Conducting Particles at Optical Frequencies [J]. Progress in Electromagnetics Research, 2006, PIER 63: 223-242.

[5] Seleznev N, Habashy T, Boyd A. Formation Properties Derived from a Multi-frequency Dielectric Measurement [C]∥SPWLA 47th Annual Logging Symposium, June 4-7, 2006.

[6] 吴亚敏, 陈国庆, 谢秉川. 椭球形介质的退极化因子 [J]. 无锡教育学院学报, 1999, 13(3): 60-64.

[7] 唐炼, 张守谦, 安丰全. 超高频岩石介电特性的研究 [J]. 测井技术, 1992, 16(5): 323-326.

[8] 唐炼, 韩有信. 高频段岩石介电频散现象的实验研究 [J]. 石油物探, 1995, 34(3): 109-113.

[9] 高卫国, 谢然红. 冀东油田介电测井实验研究 [J]. 测井技术, 2000, 24(2): 83-87.

[10] 冯启宁, 李晓明, 郑和华. 1 kHz～15 MHz岩石介电常数的实验研究 [J]. 地球物理学报, 1995, 38(1): 331-335.