利用贝叶斯判别法识别岩性基础上的孔隙度评价

袁少阳, 张占松, 李权, 石文睿

(油气资源与勘探技术教育部重点实验室(长江大学), 湖北 武汉 430100)

0 引 言

复杂储层具有孔隙空间类型多样、岩性复杂、非均质性强等特点,有着极其复杂的岩石物理响应,如果不对储层分类评价,将难以建立准确的测井响应理论模型,且储层的非线性、非均质性导致测井解释的多解性[1]。依据岩性对储层进行分类,每一类岩性都有其对应的孔隙结构,各类孔隙结构对应不同的测井曲线特征。孔隙度的准确计算是油藏精细评价的基础[2]。为了提高伊位克M油田复杂岩性储层的计算孔隙度的精度,本文采用最小错误率的贝叶斯判别法先进行岩性判别,根据岩性选择不同的孔隙度计算模型,将计算出的孔隙度与不进行岩性分类而直接计算的孔隙度对比,发现分类后可以得到较高精度的计算孔隙度。

1 研究区地质概况

研究区位于伊拉克M油田,其地质构造格局主要是由三次大规模的造山运动所决定的,分别是元古宙晚期-显生宙早期的泛非运动,古生代晚期-中生代早期的印支-海西运动,以及新生代的喜马拉雅造山运动,最终形成了构造走向以北西—南东为主的现今构造格局[3],在复杂的构造条件下形成了该地区较为复杂的岩性类别和储集空间。研究区的储集空间以孔隙型为主,但也含有较多裂缝型和裂缝-孔隙型。分析薄片资料可知,孔隙包括有粒间孔隙以及粒内溶孔、铸模孔、晶间孔隙等次生孔隙。分析岩心物性资料和裂缝数据可知,孔隙度主要分布在4%～12%,渗透率分布在0.2～5 mD*非法定计量单位,1 mD=9.87×10-4 μm2; 1 ft=12 in=0.304 8 m,下同,属于低孔隙度低渗透率储层[4]。一些垂直裂缝和多向裂缝的存在也使一些层段有较大的渗透率,但也并不一定是较好的储集层。

分析M油田的取心录井资料,研究区的岩性复杂,各类岩性分布比例如图1所示。层位上从上到下大体的岩性分布趋势为白云岩储层、含砂岩夹层的白云岩,深层主要为灰岩、 薄层泥页岩,以及含白云岩夹层的砂岩储层。不同的岩性类别具有不同的骨架值和测井响应特征,以岩性识别为基础建立孔隙度模型可以更有效地计算孔隙度。

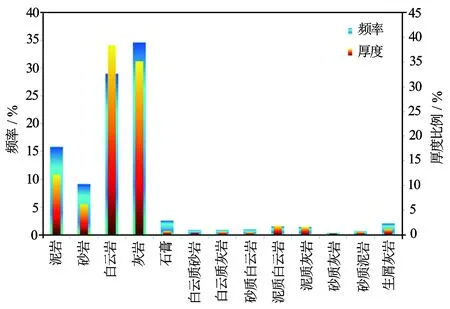
图1 M油田岩性分布比例

2 岩性判别基础上的孔隙度计算

孔隙度的常规计算方法主要是体积模型法和岩心刻度法。最常用的纯岩石水层体积模型的使用有2个前提条件:①地层不含泥质或泥质含量稳定;②孔隙度在15%～30%的范围内变化[5]。在岩性相对复杂的低孔隙度低渗透率储层中直接利用体积模型法并不能较准确反映储层孔隙度。对于岩心刻度法,对比M地区测井资料和取心、录井资料发现,孔隙度与各测井曲线相关系数都较低(见表1)。从图2看出,岩心孔隙度与密度、声波时差呈现出散乱的对应关系。分析其原因主要是研究区岩性复杂,不同的岩性具有不同的岩性骨架值,混杂岩性如泥质或膏质的影响造成了交会点的散乱分布。结合一些数学方法以提高孔隙度的计算精度是有必要的[6]。

图2 孔隙度与密度、声波时差交会图

ACRHOBNPHIGRRLLdϕ0.301-0.4670.4140.053-0.282

2.1 利用贝叶斯判别法进行岩性识别

基于研究区的复杂岩性特征,先利用模式识别方法识别岩性,再计算孔隙度。贝叶斯判别法是统计模型决策中的基本方法,在不完全已知所有的情况下对于部分未知的状态用主观概率估计,用贝叶斯公式对发生概率进行修正,最后利用期望值和修正概率作出最优决策[7]。本文是将岩性识别看作是种类判别问题,从最小错误率的要求出发,利用贝叶斯公式得出使错误率最小的分类决策[8]。

整个岩性识别过程。①根据岩性描述初步了解研究区的主要岩性,根据岩性的分布情况进行判别岩性的大体分类。贝叶斯判别所要求的数据应服从正态分布,只有当均匀抽样时才能满足这一条件。为了大致使各种分类的先验概率相等,研究区共有十几口研究井,选择了其中的5口井建立了岩性样本。②选择特征最显著、曲线最齐全的1口井作为关键井,对研究区作了测井曲线标准化。③选择合适的测井曲线作为输入曲线,利用贝叶斯判别法编写了程序,形成贝叶斯判别分类器。其中,后验概率是利用贝叶斯公式求得

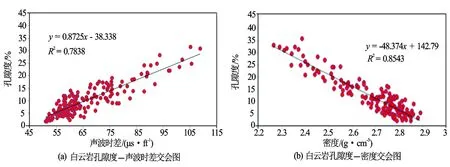
图3 白云岩单条测井曲线拟合模型示意图

(1)

式中,P(ωi|x)为后验概率;p(x|ωi)为概率密度函数;P(ωi)为先验概率。利用式(1)计算每个深度点的各类训练样本的后验概率值,选取其最大值所对应的岩性类别作为该深度点的类,满足最小错误率的要求。④对样本的回判率和检验井的判别结果进行分析,调整岩性分类和测井曲线组合。选取了回判率最高的一组测井曲线组合,判别用到的测井曲线分别为自然伽马、声波时差、补偿中子、补偿密度和深电阻率曲线。表2为5口验证井的回判率。⑤重复上2步操作直到得到比较准确的岩性判别结果,最后将岩性判定为泥质灰岩、灰岩、粉砂质灰岩、白云岩、砂岩、砂质泥岩、泥岩、石膏等8种岩性。判别后以数字形式输出一条连续的方波曲线。

表2 各验证井训练样本回判率

2.2 基于岩性判别的孔隙度计算

在依据岩性分类的基础上选择各岩性较为典型的数据点,排除裂缝层位和边界点,利用岩心分析孔隙度与三孔隙度曲线分别建立了测井解释模型,孔隙度与测井曲线之间体现出较好的相关性。图3为白云岩孔隙度与声波时差和补偿密度的拟合模型。

用单条测井曲线拟合模型的数据进行多元拟合后,得到6大类岩性最终用于计算的岩性刻度模型:

白云岩φ=34.907+0.556AC-20.257RHOB-0.028NPHI

灰岩φ=34.251+0.372AC-19.702RHOB+0.379NPHI

砂岩φ=16.827+0.057AC-8.940RHOB+0.907NPHI

泥质灰岩φ=-57.212RHOB+154.46

石膏、泥岩φ=0

式中,φ为计算孔隙度;AC、RHOB、NPHI分别为声波时差、补偿中子、补偿密度孔隙度曲线。

对于岩性分类中的粉砂质灰岩和砂质泥岩由于砂质的存在没有较好的拟合模型,在计算过程中直接使用灰岩和泥岩的解释模型。计算时会根据岩性分类器输出的岩性数字代码而选择不同的测井解释模型,从而有效计算孔隙度。

根据岩石物理体积模型原理,孔隙度测井值可以看成是在测井仪器的探测范围内地层岩石各组分的相对体积与对应的测井物理量乘积的总和。运用体积模型的关键主要是参数的选择,而M地区的复杂岩性特征使单一或常规的岩石骨架值都不能较准确计算整口井的孔隙度值。通过前文所述的交会图可以确定各类岩石骨架值,在岩性识别后自动选择各岩性所对应的骨架参数,大大提高了孔隙度的计算精度。骨架值、泥质及流体参数的选择见表3。

表3 各岩性的骨架参数及孔隙流体参数

除了以上4种岩性外,泥质灰岩和粉砂质灰岩计算时也使用灰岩的骨架密度值,砂质泥岩与泥岩一样同等于0。将骨架参数代入体积模型计算公式也可较好地计算孔隙度。补偿密度计算孔隙度

(2)

式中,ρb、ρma、ρsh、ρf分别为地层、骨架、泥岩、流体密度测井值,g/cm3。

补偿中子计算孔隙度

(3)

声波时差计算孔隙度

(4)

式中,Δt、Δtma、Δtsh、Δtf分别为地层、骨架、泥岩、流体声波测井值,μs/ft;Cp为地层压实校正系数。

中子—密度测井值交会计算孔隙度

φ=(φD+φN)/2

(5)

3 孔隙度的评价与分析实例

以伊拉克M油田×-3井为例计算储层孔隙度,编写好所需的贝叶斯决策分类器和跟据岩性选择不同的孔隙度计算模型程序,可以得到分别由体积模型法和岩心刻度法计算的2类孔隙度。图4是×-3井通过2种算法计算的孔隙度;图4中判别岩性与录井岩性符合率很高,计算孔隙度中第1列和第2列是基于岩性识别后利用岩心刻度法与体积法计算的;第3列是直接利用补偿密度的体积模型公式计算的。显然,前2列计算值与岩心分析孔隙度有较好的一致性,第3列计算值整体偏小。

图4 ×-3井孔隙度计算结果示意图

×-3井,基于岩性识别后利用体积模型法计算的孔隙度平均绝对误差为1.46%,平均相对误差为16.37%,利用岩心刻度法计算的孔隙度平均绝对误差为2.51%,平均相对误差为25.32%;直接利用体积模型计算平均绝对误差为4.57%,平均相对误差为48.3%。由此可见,基于贝叶斯判别法的孔隙度计算方法可以有效提高孔隙度的计算精度,达到精细评价储层的目的。表4为M油田8口井的孔隙度计算结果。

图4和表4中,利用体积模型法所计算孔隙度的误差值要小于岩心刻度法可以计算出更高精度的孔隙度值,在评价M油田复杂储层中利用贝叶斯判别法判别岩性后再利用体积模型的计算方法更为有效。

表4 各井孔隙度计算结果误差分析表

4 结 论

(1) 对于复杂岩性储层的测井评价可以考虑分岩性进行研究,每一类岩性在测井曲线特征上都有一定的共性,找出其特征值进行岩性分类,可以更好地进行储层评价。

监督责任不够明晰。监督必须要承担责任，不然监督可有可无。但在实践当中，纪检监察人员严格执行制度却经常被贴上不愿担责、缺乏担当的标签，究其原因，是制度规定不够明晰，对监督失职、渎职行为虽然有处罚规定，处罚也很严厉，但依据怎样的标准来定性却较为笼统，被监督部门往往以“出了问题还是我们担责，又不会追你们的责”为由来搪塞；比如招投标承办部门只在开标前通知纪检部门参与监督，是不是做到了事前报告；这时候不监督是失职，监督了怕违规，参与还是不参与，责任如何界定；相关制度却没有明确规定，很多时候显得左右为难。

(2) 利用贝叶斯算法可以综合考虑多方面的测井参数有效识别岩性,消除对模型无关的信息干扰,在不同层位选取最有效的计算模型,可以明显提高孔隙度的计算精度。基于岩性识别的基础,岩心刻度和体积模型2种传统的孔隙度计算方法都可以完成较准确的计算。

(3) 伊位克M油田体积模型的方法比岩心刻度法更能够准确计算孔隙度,选取贝叶斯判别法识别岩性与体积模型法的组合去计算孔隙度可以较好地支持该地区的油藏精细评价工作。

参考文献:

[1] 王树寅, 李晓光, 石强, 等. 复杂储层测井评价原理和方法 [M]. 北京: 石油工业出版社, 2006.

[2] 雍世和, 张超谟. 测井数据处理与综合解释 [M]. 东营: 中国石油大学出版社, 2007.

[3] 韩耀祖, 陈伟, 欧成华, 等. 伊拉克米桑地区阿布古拉卜背斜的几何解析和运动学模拟 [J]. 新疆石油地质, 2014, 35(1): 124-129.

[4] 朱筱敏. 沉积岩石学 [M]. 4版. 北京: 石油工业出版社, 2008.

[5] 袁晓宇, 张哨楠, 李映涛, 等. 非线性有效孔隙度计算方法研究 [J]. 测井技术, 2013, 37(2): 173-176.

[6] 范铭涛, 沈全意, 吴辉, 等. 复杂岩性裂缝-孔隙型储层孔隙度计算方法研究 [J]. 天然气工业, 2005, 25(5): 29-36.

[7] 毛宁波, 王浩, 谢涛, 等. 贝叶斯判别法在GD地区叠前地震属性交会中的应用 [J]. 石油天然气学报(江汉石油学院学报), 2010, 32(5): 95-98.

[8] 宋秋强, 张占松, 张冲, 等. 测井相-岩相分析技术有复杂岩性中的应用 [J]. 石油天然气学报(江汉石油学院学报), 2013, 35(6): 1-4.