组合导航系统中自适应迭代粒子滤波

黄春梅，　邹慧莹，　王　杰

(长春工业大学 计算机科学与工程学院， 吉林 长春　130012)



组合导航系统中自适应迭代粒子滤波

黄春梅，邹慧莹*，王杰

(长春工业大学 计算机科学与工程学院， 吉林 长春130012)

摘要：提出一种自适应迭代粒子滤波算法，利用自身迭代实时更新重要密度函数，快速将粒子推到高似然区，让粒子权重分散均匀，提高采样效率。运用模拟退火算法来解决粒子权重很小、不易归一化的问题,仿真结果可知，自适应迭代粒子滤波算法在SINS/GPS组合导航中有更好的实用性。

关键词：SINS/GPS组合导航； 标准粒子滤波； 迭代粒子滤波； 退火算法

0引言

在SINS/GPS组合导航系统中，解算精度与高精度非线性的滤波算法有很大关系[1]。主要的非线性滤波算法有扩展卡尔曼滤波(EKF)、Unscented卡尔曼滤波(UKF)、粒子滤波等。EKF利用Taylor公式对组合导航系统模型进行线性化，忽略掉所有误差的二次项及高于二次项的误差项，当系统模型非线性化很强的时候，滤波效果明显下降[2]；UKF利用非线性系统的已知数学模型和初始状态的均值、方差来获得一组权值函数以及一组样本点，不需要对系统模型进行线性化变换，但是其需要假设噪声满足高斯分布，而且系统维数较高就增加其计算量[3]；标准粒子滤波基于蒙特卡洛模拟和贝叶斯估计理论，直接利用非线性系统完成非线性变换，避免了线性化的系统高阶误差影响，但是粒子滤波会出现重要性密度函数难以选取和粒子退化等问题[4]。

针对上述标准粒子滤波出现的问题进行改进，提出了一种利用自身迭代来更新重要性密度函数的自适应迭代粒子滤波方法。当重要性密度函数的高斯分布超出了预定的阈值，自适应迭代粒子滤波算法就利用修正项自身迭代实时更新重要性密度函数，然后再利用模拟退火算法和自适应退火参数来解决粒子归一化权重相同的问题，将粒子快速推入高似然区域，以提高采样效率[5]。

1SINS/GPS系统的非线性模型[6]

SINS/GPS系统结构如图1所示。

图1SINS/GPS系统结构图

在SINS/GPS组合导航中采用的是东-北-天坐标系， GPS接收机得到的位置、速度和SINS解算出来的位置、速度相减，差值作为组合滤波器的输入，然后组合滤波器的输出采用反馈校正，陀螺仪和加速度计漂移误差的校正在SINS中进行，而位置和速度信息直接对SINS的解算结果进行校正。

1.1SINS/GPS状态方程

误差状态向量：

由位置误差、速度误差、姿态误差角、加速度计零偏误差以及陀螺仪漂移误差等组成。

1)位置误差方程：

(1)

2)速度误差方程：

(2)

3)平台误差方程：

(3)

式中----载体坐标系到导航坐标系的转换矩阵；

εb----载体坐标系中的陀螺仪漂移。

将式(1)～式(3)综合，得到状态方程：

(4)

式中：FI----系统状态矩阵；

WI----系统噪声；

GI----系统噪声矩阵。

1.2SINS/GPS量测方程

组合系统的量测信息是SINS解算的位置、速度与GPS测量到的位置、速度之差。

1)位置量测误差：

(5)

式中：λ、L、R----分别为经度、纬度、地球半径；

nx，ny，nz----分别为GPS 接收机沿地理坐标系x、y、z三个轴方向上的位置误差噪声。

2)速度量测误差：

(6)

式中：nvx，nvy，nvz----分别为GPS 接收机沿地理坐标系x、y、z三个轴方向上的速度误差噪声。

将式(5)与式(6)合并，得量测方程：

(7)

2标准粒子滤波算法[7]

假设离散化系统状态方程和量测方程：

(8)

(9)

vk-1和wk是过程噪声和量测噪声，相互独立。f(·)和h(·)是已知的函数。

标准粒子滤波步骤如下：

1)初始化。

2)更新。

在k时刻，更新粒子的权值

(10)

并且归一化

(11)

则k时刻x的最小均方估计为

(12)

3)重采样。

得到新的粒子集合

4)预测。

5)时刻k=k+1，转到步骤2)。

在标准粒子滤波算法中，权重的方差随时间而随机递增，使得少数粒子拥有较大权重，最后很可能导致大量的计算工作浪费，粒子集无法表达实际的后验概率，产生了粒子退化的问题。

3自适应迭代粒子滤波算法

自适应迭代粒子滤波的基本思想就是利用粒子滤波自身迭代修正，产生新的IDF，并在模拟退火算法的帮助下将粒子推入高似然区。

假设已知

且有过程噪声和量测噪声的协方差分别为：

设定阈值ρ，如果

该粒子有效，用重采样技术估计xk；否则，就用更新等式产生新的IDF。更新的等式如下：

(13)

式中：c(zk)----修正项。

粒子滤波利用其自身迭代修正项c(zk)。用cm(zk)表示第m次迭代，则有：

(14)

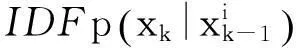
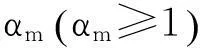
(15)

其中

(16)

使

(17)

使

得：

(18)

自适应迭代粒子滤波步骤如下：

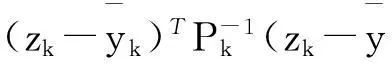
2)更新IDF。更新公式为：

第m次迭代产生新的IDF为:

3)归一化权值。引入退火参数αm(αm≥1)，协方差为αmRk。粒子的权值越大越好，则需要成本函数:

最大化。退火参数αm=max{1,1/βm}，而粒子权值

然后归一化

4)重采样。从新等到的IDF中得到粒子集合。

6)判断是否采样结束，否则继续以上步骤采样。

4仿真分析

标准粒子滤波速度误差和自适应迭代粒子滤波速度误差分别如图2和图3所示。

对上述两种方法进行仿真分析。通过图2与图3分析比较可以得出，标准粒子滤波东-北-天3个方向的速度误差范围分别为-0.85～ +1.00 m/s、-0.95 ～ 0.91 m/s、-1.00～ 0.78 m/s，自适应迭代粒子滤波东-北-天3个方向的速度误差范围分别为-0.32～ +0.51 m/s、-0.29 ～ +0.73 m/s、-0.46～ +0.34 m/s。

标准粒子滤波位置误差和自适应迭代粒子滤波位置误差分别如图4和图5所示。

通过图4与图5的分析比较得出，标准粒子滤波东-北-天3个方向的位置误差范围为-8.93～ +9.12 m、-10.00～ +9.53 m、-10.00～ +9.47 m，自适应迭代粒子滤波东-北-天3个方向的位置误差范围为-4.67～ +6.03 m、-3.65～ +5.21 m、-4.86～ +5.07 m。

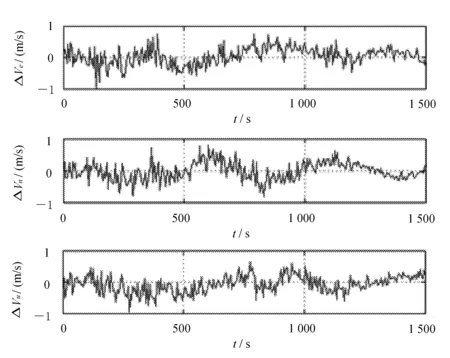
图2标准粒子滤波速度误差

图3　自适应迭代粒子滤波速度误差

5结语

自适应迭代粒子滤波算法在粒子滤波算法重采样的基础上进行改进，利用滤波本身来进行自适应迭代，从而使粒子快速进入高似然区域，又基于粒子权重逐渐集中于少数粒子上，并且自适应的修正项慢慢趋近于零值的问题，利用模拟退火参数来解决，让成本函数最大化，得到的最大解就是所需的参数，从而解决了粒子滤波中粒子退化问题，通过相关性能比较，所提出的改进算法的有效性得以验证。

图4标准粒子滤波位置误差

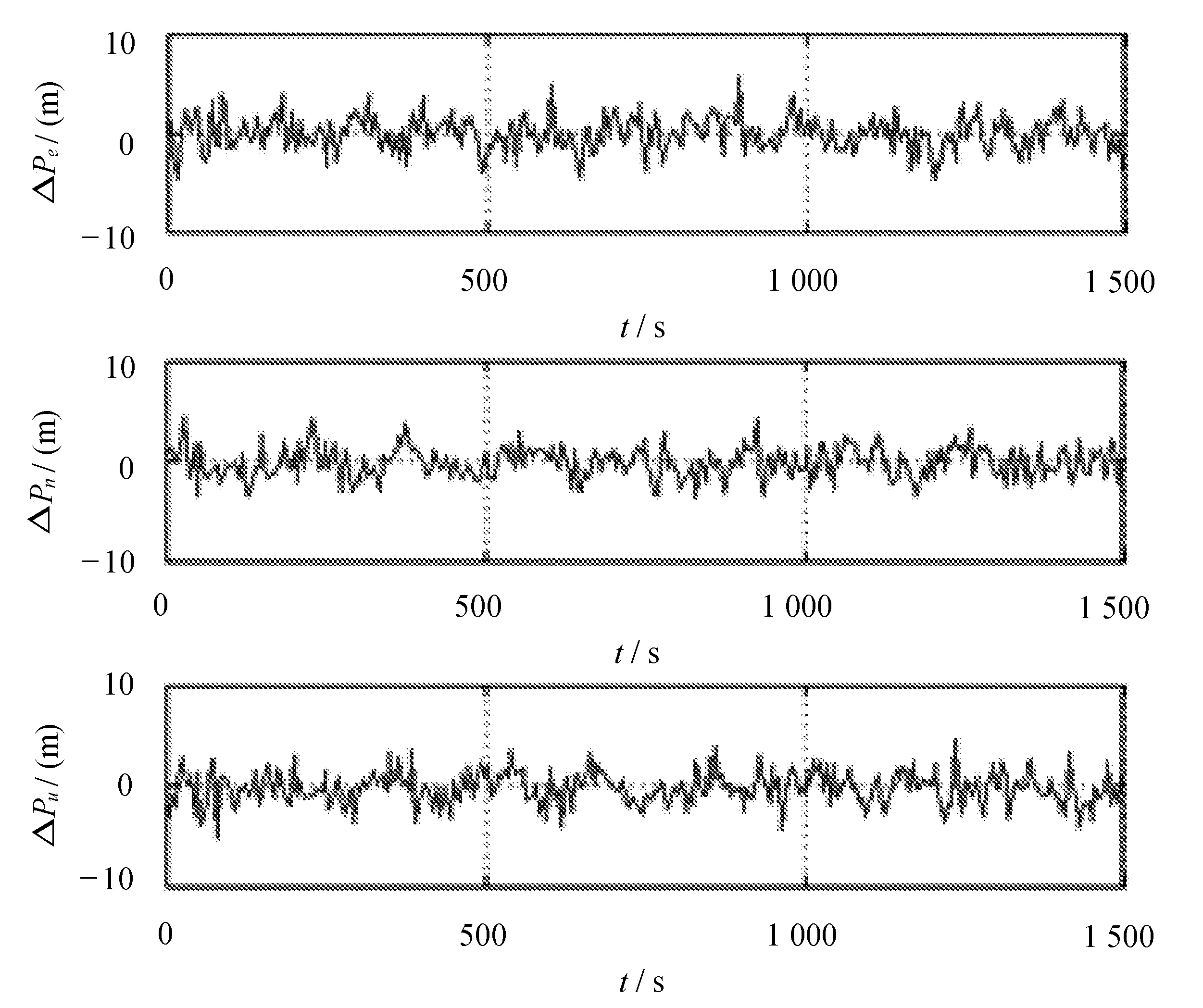
图5　自适应迭代粒子滤波位置误差

参考文献：

[1]王健.提高SINS/GPS组合导航系统定位精度的方法研究[J].现代导航，2014，2(1)：7-10.

[2]刘毛毛，秦品乐，吕国宏,等.基于多新息理论的EKF改进算法[J].计算机应用研究，2015,32:1568-1571.

[3]汲清波，冯驰，吕晓凤.UKF、PF与UPF跟踪性能的比较[J].计算机工程与应用，2008，44(32)：60-63.

[4]王法胜，鲁明羽，赵清杰,等.粒子滤波算法[J].计算机学报，2014，37(8):1679-1694.

[5]Zhouhua Duan， Zixing Cai， Jinxia Yu. Adaptive particle filter for unknown fault detection of wheeled mobile robots[J]. Proc. of IEEE/RSJ International Conference on Intelligent Robots and Systems， Beijing， China， Oct.，2006：1312-1315.

[6]王新龙，李亚峰，纪新春.SINS/GPS组合导航技术[M].北京：北京航空航天大学出版社，2014.

[7]J Y Zuo， Y N Jia， Y Z Zhang， et al. Adaptive iterated particle filter[J]. Electronics Letters，2013,49(12)：724-744.

[8]A Rahni， E Lewis， M Guy， et al. A particle filter approach to respiratory motion estimation in nuclear medicine imaging[J]. IEEE Transactions on Nuclear Science，2011,58(5)：2276-2285.

Adaptive iterated particle filter in integrated navigation system

HUANG Chunmei,ZOU Huiying*,WANG Jie

(School of Computer Science & Engineering, Changchun University of Technology, Changchun 130012， China)

Abstract：An adaptive iterated particle filter (AIPF)is put forward, in which self-update is applied to update the importance density function in real time for pushing the particles to the high likelihood region quickly, so the particle weight can be evenly distributed to improve the sample efficiency. An annealing algorithm is used to solve the problem that the particle weight is too small to normalize. Simulation results demonstrate that the adaptive iterated particle filter is practical for SINS/GPS integrated navigation system.

Key words：SINS/GPS integrated navigation system; particle filter; iterated particle filter; annealing algorithm.

中图分类号：TP 274

文献标志码：A

文章编号：1674-1374(2016)01-0030-06

DOI:10.15923/j.cnki.cn22-1382/t.2016.1.07

作者简介：黄春梅(1965-)，女，汉族，吉林长春人，长春工业大学副教授，博士，主要从事嵌入式控制方向研究,E-mail:huangchunmei@ccut.edu.cn. *通讯作者：邹慧莹(1990-)，女，汉族，湖北荆门人，长春工业大学硕士研究生，主要从事嵌入式控制方向研究,E-mail:ssmilezou@163.com.

收稿日期：2015-11-23