基于混合逻辑动态模型的逆变器开路故障诊断

葛兴来，苟 斌，蒲俊楷，王志远

(西南交通大学 电气工程学院，四川 成都 610031)

逆变器是现代工业变压变频控制交流传动系统的核心。在轨道交通、大规模发电机组、航空、军事等场合，逆变器发生故障将带来不可估量的损失，因此如何在线监测电机驱动系统运行状态引起人们的广泛关注[1]。

在电机驱动系统中，功率变换环节尤其是逆变器中的电力电子器件及其驱动电路是容易发生故障的薄弱环节[2]。IGBT常见故障主要有过电流故障、过电压故障、欠电压故障、过热故障、过载故障等[3]，这些常规故障保护电路在智能功率模块中已经形成一个标准，在一定程度上保证了逆变器的安全运行。

文献[4，5]将快速熔断器引入到逆变器桥臂中，可以将短路故障转化为开路故障诊断。目前逆变器开路故障诊断方法主要通过检测三相电压和三相电流实现，其中多数为基于三相电流检测，而诊断方法主要分为基于信号处理和基于模型两大类。

文献[6]搭建简单硬件电路检测上桥臂开关和下桥臂开关电压，当发生开路故障时，其实际值与正常时不同，依据其误差来诊断定位故障，方法简单实用，但是实际电路由于噪声干扰等存在，易出现误诊断现象。文献[7]利用逆变器相电压、逆变器桥臂中性点对地电压以及电机线电压实际值与理论值误差，经过滞环比较器，通过查表定位故障。为了避免测量和噪声误差带来的误诊断，将实际电压和理论电压低通滤波后诊断，造成诊断时间延长。总体来说电压诊断法简单，诊断时间短，但需要增加额外的传感器，且容易受到环境干扰。

文献[8]利用3s/2s变换将三相电流变换到两相坐标系中，根据空间电压矢量位置来定位故障，但是在负载较小时，受测量误差和噪声干扰等影响，易出现误诊断或者定位错误。文献[9]利用三相电流一个周期内的平均值为零，将三相电流转换为Clark坐标下平均电流Park矢量，根据矢量不同的相位角判断IGBT开路以及短路故障，取平均电流Park矢量提高了系统的抗干扰性能，但同时也增加了诊断时间，且阈值的选取跟负载有较大关系，由于变频调速引起的三相电流频率不断变化导致电流平均值求取困难，易造成误诊断。此外，还有学者通过信号处理方法提取故障电流波形中隐含信息，通过小波分析或者神经网络进行故障诊断。

混杂系统MLD(Mixed Logic Dynamic)是将离散动态和连续动态有效结合起来的一种统一的模型框架结构，目前已广泛应用于各个领域。文献[10]将MLD应用于三相逆变电路，通过建立三个故障事件观测模型，当发生对应故障时，相应残差为0。文献[2]建立逆变器+同步电机模型，通过坐标变换将三相残差变换到两相静止坐标系下，通过矢量位置定位故障。

本文建立三相逆变器混杂系统模型，以三相残差电流为观测量，根据电流变化规律建立故障信息表，并通过阈值抑制噪声和测量误差等影响，当IGBT发生开路故障后，通过残差信息表迅速诊断定位故障。

1 电机驱动系统混合逻辑建模

1.1 混合逻辑建模步骤

混合逻辑动态模型包含了离散和连续状态以及两者之间在约束下的系统转换，其中连续状态变量随着时间的变化而变化，而离散变量由外在事件驱动变化。整个系统的运转由两者共同驱动，外在的驱动通过离散变量传递给系统，从而获得系统模式上的转换，而在不同的状态空间内，遵循电力电子器件模型规则变化；连续变量同样会影响离散事件的状态，例如当IGBT两端电压为负，即使开关信号为1，IGBT仍然不会导通。

MLD模型将离散变量和连续变量根据逻辑运算法则转化为混合不等式，其建立步骤如下。

(1)建立系统连续部分状态空间方程。

(2)建立系统约束对应的命题逻辑，命题的真值由逻辑变量δ∈(0,1)表示，通过命题之间的规则关系将简单命题转化为复合命题，通过辅助变量z建立混合整数不等式。

(3)将离散变量和连续变量融入到线性时不变动态系统中，用统一的混杂系统模型描述两个部分对系统变化的共同作用。

MLD模型的一般形式为

( 1 )

式中:x=(xc,xd)T为状态变量，其中xc为连续变量，xd为离散状态；输出变量为y(t)，同样包含连续输出yc和离散输出yd；δ和z分别为辅助逻辑变量和辅助连续变量；A、B1～B3、C、D1～D3分别为系数矩阵。

1.2 逆变器和电机建模

图1给出了电机驱动系统组成和结构，通过传感器采集三相电流和电机转速，经过矢量控制和空间矢量调制，最终输出s1～s6开关信号，控制逆变器IGBT的导通和关断进而实现变压变频调速。在电机驱动过程中，频繁的启动、加速、减速增加了实时在线故障诊断的难度，而通过混合逻辑模型诊断恰恰是通过检测估计电压电流瞬时值，为实时诊断提供了可能。为了进一步分析电机驱动系统正常运行乃至故障运行模式下内部运行机制，有必要通过混合逻辑建模方法对系统进行建模，根据模型来对其故障进行诊断。

图1 控制框图

简化后的电机状态方程为

( 2 )

式中：uan、ubn、ucn为定子相电压瞬时值；ia、ib、ic为定子相电流瞬时值；ea、eb、ec为三相反电动势；Rs为定子每相绕组电阻。

根据电路拓扑和电路约束关系可得

( 3 )

由星形连接绕组可知uan+ubn+ucn=0，则有

( 4 )

由式( 3 )、式( 4 )可得

( 5 )

逆变器主要由6个IGBT和6个二极管构成。IGBT的导通与关断受驱动信号的控制，而二极管的导通与关断受端电压正负驱使。IGBT和二极管的变化均会导致传动系统模态的变化，故将IGBT的导通与否定义为控制变量，相应开关信号则为离散控制变量，而二极管的导通与否受电流方向控制，属于条件变量，等价于离散条件变量，这是系统本身的特性，也正是因为这种特性使得逆变器能够输出给定频率的电压信号从而驱动电机运转。当IGBT发生故障后，必将使系统发生不正常的跳变，与系统原有的控制相背离。传统的逆变器模型通常只考虑IGBT控制信号变化，未曾考虑由于电流变化导致的二极管开关变化，所以无法判断在死区时系统的运行状态。通过建立传动系统的混合逻辑动态模型，能够有效地避免这些不足。系统本应发生的电流变化与故障后的不正常电流变化进行对比，能够有效定位故障点。首先引入3个辅助变量σa、σb、σc等效条件变化。

[σa=1]↔[ia>0]

[σa=0]↔[ia<0]

( 6 )

[σb=1]↔[ib>0]

[σb=0]↔[ib<0]

( 7 )

[σc=1]↔[ic>0]

[σc=0]↔[ic<0]

( 8 )

逆变器包含有6个开关信号离散控制变量和σa、σb、σc三个离散条件变量，显然由9个逻辑变量可能出现29=512种组合，以A相为例，结合A相桥臂开关信号和式( 6 )可以得到A相电压定子侧对中间直流环节中点电压信号真值表，见表1。

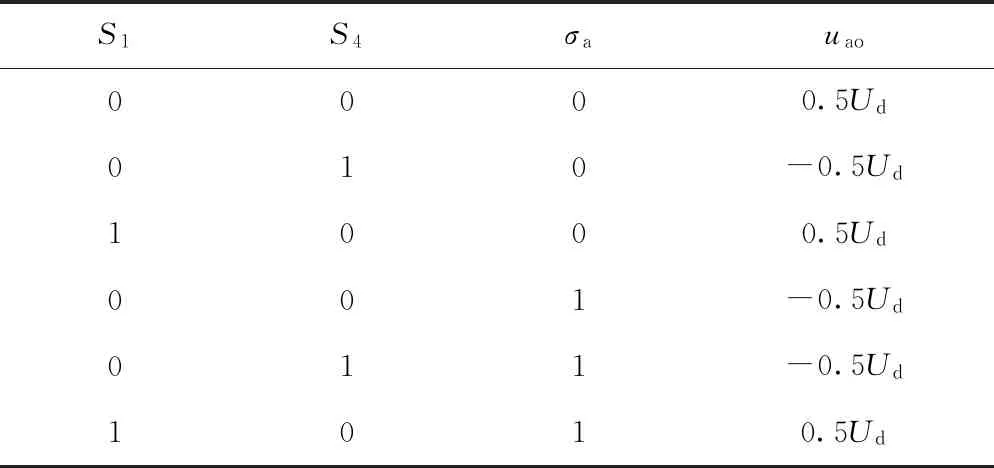
表1 电压信号uao真值表

根据表1可得

[S1=0,S4=0,σa=0]∨[S1=1,S4=0,σa=0]
∨[S1=1,S4=0,σa=1]↔[uao=0.5Ud]
[S1=0,S4=1,σa=0]∨[S1=0,S4=0,σa=1]
∨[S1=0,S4=1,σa=1]↔[uao=-0.5Ud]

( 9 )

通过逻辑变换可得

(10)

由式( 9 )和式( 5 )可得

(11)

由式(11)和式( 2 )可以得到电机驱动系统状态估计方程为

(12)

异步电机三相感应电动势为

(13)

至此建立了完整的电机驱动系统MLD模型，整个系统运转符合状态估计方程式(12)。

2 基于电流残差的故障诊断

在电机驱动系统中，主要通过控制IGBT的开通和关断输出幅频可调的三相电压驱动电机。将IGBT开关信号转化为离散变量，建立电机驱动系统状态模型。由式(12)可知，离散变量δ决定了系统模态和最终输出。无故障时，δ和系统实际值一致，误差为零。当开关管发生故障时，δ估计值和系统实际值不一致，导致输出电流误差发生变化，残差出现较大变化，以A相上桥臂为例分析，即s1恒等于0，代入式(12)得到其实际系统输入为

(14)

定子三相残差电流为

(15)

其解为

(16)

根据输入开关信号和电流信号变化，残差值分为以下几种情况。

工作模式1：

工作模式2：

工作模式3：

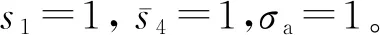
(17)

在工作模式1下，A相上桥臂开关管不导通，其故障与否对系统无影响；工作模式2下，A相上桥臂开关管给予导通信号，但是电流经二极管续流，这种工作模式极少发生；工作模式3下，三相残差单调上升或下降。结合三种工作模式可知三相残差电流呈阶梯型单调上升或下降，达到积分上限，最后可通过残差信息表定位故障。无故障时残差电流大约为±30 A以内，为了抑制噪声和测量误差，设定阈值h1=±200 A，当残差超过±200 A后，保持输出。残差信息见表2。

表2 残差信息

图2给出了逆变器故障诊断框图，通过MLD模型估测定子三相电流，然后计算残差，当三相残差均大于阈值h1时，对应残差信息表定位故障。

图2 逆变器IGBT故障诊断框图

3 仿真与半实物验证

在MATLB/Simulink仿真环境下进行验证。选用三相异步电机参数如下：定子电阻0.106 5 Ω；转子电阻0.066 3 Ω；定子漏电感1.31 mH；转子漏电感1.93 mH；互感53.6 mH；极对数2；转动惯量460 kg·m2。如图1电路拓扑，直流侧电压Ud=3 000 V，逆变器开关周期为500 Hz，负载转矩为0，给定转速ω=300 rad/s。

图3给出了无故障条件下，A相估计电流和实际电流波形以及残差。从图3可以看出，估计电流和实际电流基本重合，残差量很小，幅值波动在50 A以内，验证了上述理论的正确性。

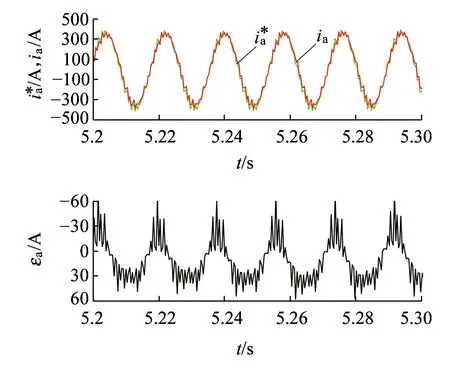
图3 A相电流实际值与估计值及残差

以A相上桥臂开关管故障为例，图4～图6分别给出了T1故障时A相、B相和C相相电流估计值、实际值及残差。当发生故障后，三相电流呈阶梯状单调递增或递减，与理论分析故障三相电流三种工作模式一致；由式(17)可知，A相残差电流常数项是B相和C相的两倍，而仿真结果中，A相残差电流达到积分上限1 000 A需要两个阶梯，而B相和C相残差电流积分到上限则需要四个阶梯，仿真和理论分析一致。在1/8周期以内，三相残差分别达到200 A和-200 A，依据表2可快速定位故障。

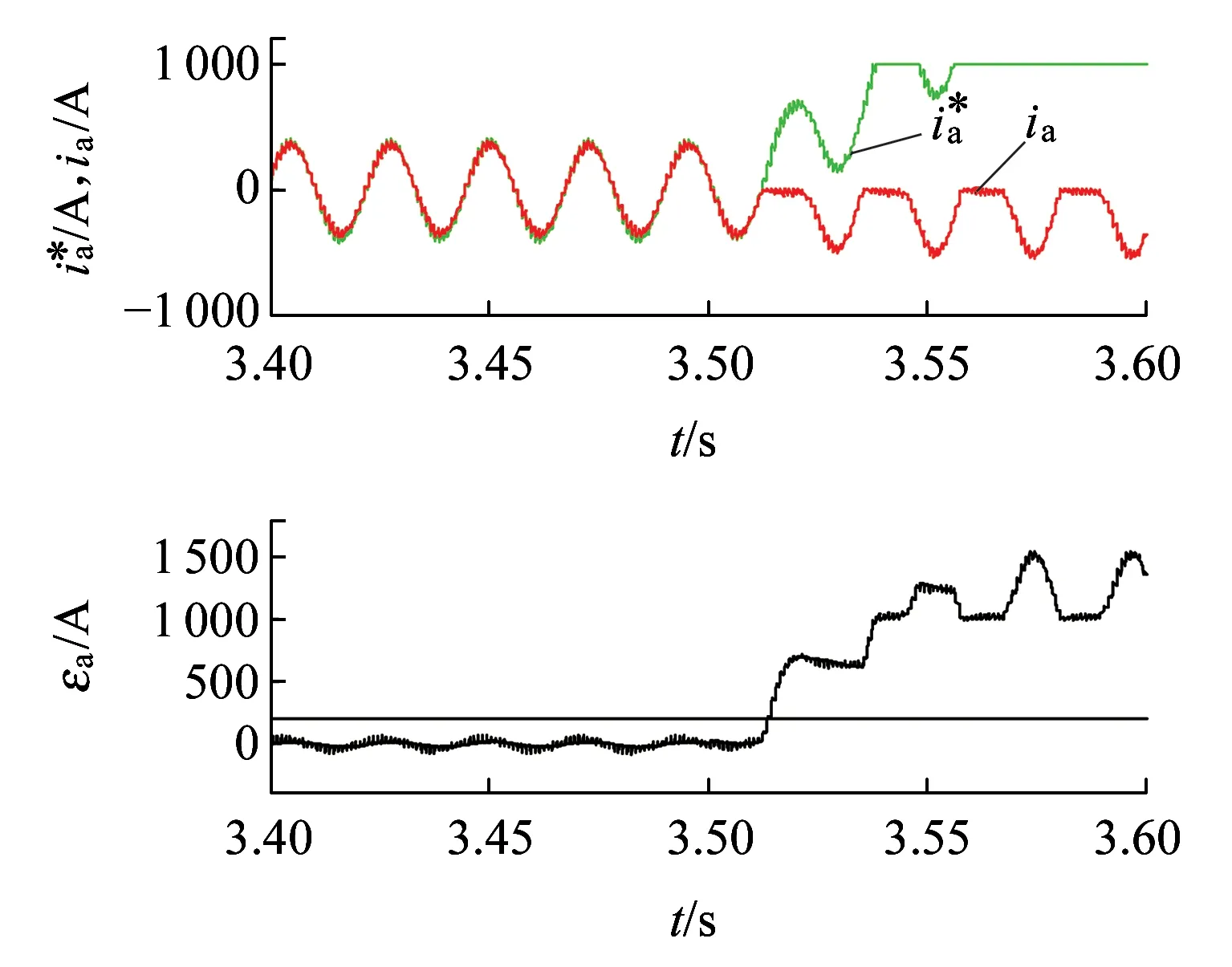
图4 T1故障前后A相电流估计值和实际值及残差

图5 T1故障前后B相电流估计值和实际值及残差

图6 T1故障前后C相电流估计值和实际值及残差

为进一步验证本文采用的基于电流残差的IGBT开路故障在线实时诊断方法的正确性，采用基于TMS320F2812和dSPACE仿真器的半实物仿真平台，进行硬件在环仿真分析，其参数与MATLB/Simulink中一致。图7～图9给出了半实物平台下三相电流故障前后估计值、实际值及残差。

图7 T1故障前后A相电流估计值和实际值及残差

图8 T1故障前后B相电流估计值和实际值及残差

图9 T1故障前后C相电流估计值和实际值及残差

由图可知，A相残差电流达到积分上限需要两个阶梯，B相和C相残差电流达到积分上限需要四个阶梯，三相残差电流εa、εb、εc均在1/8周期以内，绝对值超过200 A，依据表2中对应信息，可在1/8个基波周期以内定位故障，与理论分析和MALTAB/Simulink仿真结果一致，验证了诊断方法的正确性和有效性。

4 结论

本文将IGBT开关信号等效为离散控制变量，二极管导通与否等效为离散条件变量，依据混合逻辑建模过程建立逆变器-电机混杂系统模型，克服了线性化方法建立逆变器模型只能显示宏观性能无法揭示瞬态现象的不足。基于此模型估计三相定子电流，并与实际值产生残差，通过残差在线定位故障，通过设定阈值避免干扰、噪声的影响。仿真和实验结果表明，该诊断方法简单有效，诊断时间仅需1/8个基波周期。

参考文献：

[1]冯晓云.电力牵引交流传动及其控制系统[M].北京:高等教育出版社,2009.

[2]安群涛.三相电机驱动系统中逆变器故障诊断与容错控制策略研究[D].哈尔滨:哈尔滨工业大学,2011.

[3]安群涛,孙醒涛,赵克,等.容错三相四开关逆变器控制策略[J].中国电机工程学报,2010,30(3):14-17.

AN Quntao,SUN Xingtao,ZHAO Ke,et al.Control Strategy for Fault-tolerant Three-phase Four-switch Inverters[J].Proceedings of the CSEE,2010,30(3):14-17.

[4]ABRAHAMSEN F,BLAABJERG F,RIES K,et al.Fuse Protection of IGBT Against Rupture[C]//Proceedings of the Nordic Workshop on Power and Industrial Electronics,2000:64-68.

[5]IOV F,BLAABJERG F,RIES K.IGBT Fuses in Voltage Source Converters[C]//Proceedings of the PCIM,2001:267-276.

[6]RIBEIRO R L A,JACOBINA C B,SILVA E R C,et al.Fault-tolerant Reversible AC Motor Drive System[J].IEEE Transactions on Industrial Electronics,2004,51(2):438-447.

[7]RIBEIRO R L,JACOBINA C B.Fault Detection of Open-switch Damage in Voltage-fed PWM Motor Drive Systems[J].IEEE Transactions on Power Electronics,2003,18(2):586-594.

[8]PEUGET R,COURTINE S,ROGNON J P.Fault Detection and Isolation on a PWM Inverter by Knowledge-based Model[J].IEEE Transactions on Industry Applications,1998,34(6):1 320-1 325.

[9]MENDES A M S,CARDOSO A J M.Voltage Source Inverter Fault Diagnosis in Variable Speed AC Drives by the Average Current Park's Vector Approach[C]//Proceedings of the IEEE International Electric Machines and Drives Conference.New York:IEEE Press,1999:703-708.

[10]李宁,李颖晖,朱喜华,等.基于混合逻辑动态模型和故障事件识别向量的新型逆变电路故障诊断[J].电网技术,2013,37(10):2 808-2 813.

LI Ning,LI Yinghui,ZHU Xihua,et al.Fault Diagnosis for Power Electronic Circuits Based on Mixed Logical Dynamic Model and Incident Identification Vcctor[J].Power System Technology,2013,37(10):2 808-2 813.