哲学视角下看全国高考的应对

林海

中图分类号：G632 文献标识码：B 文章编号：1002-7661（2016）08-091-02

福建省2016年高考将启动全国卷，很多家长师生对此都比较忧虑，担心不适应考不好等。笔者认真研究了近几年考题发现，其实使用全国卷相比福建卷有自身的优劣，只要我们正确地分析，合理地应对，便能笑傲六月。哲学上有经典的三问：“是什么？为什么？怎么办”，我们不妨也试着这样思考高考及其应对策略，提出高考复习三问：“考什么？怎么学？怎么考？”

一、考什么

从表上我们很容易看出全国卷突出对六大主干知识的考查，分值近120分，大题小题和题序的分布总体稳定。解答题5道大题分别为三角或数列、概率统计、立几、解几、函数导数，题序上依次是三角或数列、概率或立几、解几、函数导数。非主干知识考查尤其以集合逻辑用语、复数、算法、二项式定理、不等式、向量这6个知识频率较高，几乎年年考查。这其实给师生有很强的导向性，甚至也可以有一定的预测。针对于各个知识点的考查情况，那就只能做真题才能进一步研究，由于篇幅限制，本文以复数和数列为例，看高考卷的考查力度。大家可以以此类推。

2011年1.复数 的共轭复数是（ ）

A. ；B. ；C. ；D.

2012年3。下面是关于复数 的四个命题：其中的真命题为（ ）

的共轭复数为 的虚部为

A。 ；B。 ；C。 ；D。

2013年2。若复数 满足 ，则z的虚部为（ ）

A。 ；B。 ； C。4； D。

2014年2。 =（ ）

A. ；B. ；C. ；D.

2015年1。设复数z满足 =i，则|z|=（ ）

A。1；B。 ；C。 ；D。2

复数重点考查复数的运算和概念。除法运算出现频率较高，概念上主要有实虚部、模长、共轭复数、对应点等。

11年理17.等比数列 的各项均为正数，且

（1）求数列 的通项公式。

（2）设 求数列 的前n项和。

12年理5。已知 为等比数列， ， ，则 （ ）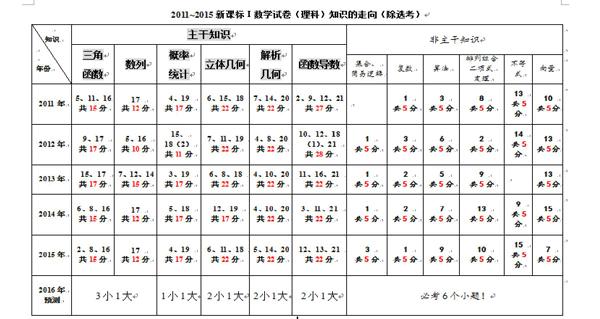

A。7； B。 5；C-5；D。-7

12年理16。数列 满足 ，则 的前 项和为

13年理7。设等差数列 的前 项和为 ，若 ， ， ，则

A。3；B。4；C。5；D。6

13年理12。设 的三边长分别为 ， ， ， 的面积为 ，

……

若 > ， ， ， ， ，则

A。 为递减数列；B。 为递增数列

C。 为递增数列， 为递减数列；D。 为递减数列， 为递增数列

13年理14。若数列 的前 项和为 ，则数列 的通项公式是 =______。

14年理17。已知数列{ }的前 项和为 ，

=1， ， ，其中 为

常数。（Ⅰ）证明： ；（Ⅱ）是否存在 ，使得{ }为等差数列？并说明理由。

15年理17 为数列 的前 项和。已知 ，

（Ⅰ）求 的通项公式：

（Ⅱ）设 ，求数列 的前 项和

数列在选填题主要考查数列的性质、公式的应用，甚至考查到了选填压轴的位置；在解答题主要考查数列证明、通项公式 与前n项和 ，其中递推公式及 与 关系需引起高度重视。

复习建议：

1、合理使用高考试卷（套卷和知识卷），对5年高考试卷做熟做透，举一反三。

2、对6+6的考点和题型清晰明白。

3、以60应对6，整理出60道典型题（尽量覆盖全部考点），反复翻看，以题知法。

二、怎么学？

数学学习水平或层次有五个境界：懂、会、熟、巧、通。

1、懂。顾名思义就是听得懂、弄得懂。如果同学上课听不懂，题目看不懂，这当然属于不懂的情况，还有学同学说我上课听得懂，就是想不到，其实这也属于不懂。如：有老师或者答案给你一个逻辑切入点，带着你往前走，最后你到了目的地。于是，你说了：这题也不难吗，我好像也能做。这是幻觉，不信换道同类型的题试试？

如若不懂，给你两个建议：1。带着问题去听课2。乐于请教和被请教。

2、会。会指的是没有老师指导，无同学帮助，无答案提示，不参考笔记的情况下，你自己能独立地完成解题。这个层次意味着你找到了解决问题的入口，能够清楚往下走的流程，并且顺利到达目的地。从懂到会，练习、练习、练习，重要的事情说三遍。

两个建议：1。基本的训练量要保证。 2。要进行专项训练和定式训练。

3、熟。在”会“的前提下，加入了解题速度的要求。一道题无时间限制，你能慢悠悠地想，慢悠悠地写，慢悠悠的算，还能检查。显然，这不是考试的状态。

考试都是限时的，要求你在短时间内拟定思路、准确运算、规范表达。

这就是好多同学的感慨：我感觉都会呀，怎么一考试都不得分呢？你是不是在时间紧迫的时候就慌了，一慌就漏洞百出了？

从会到熟，给你三个建议：1。做一定的变式训2。做错题本3。提高运算的速度和准度

可以肯定地讲，到达“熟”这个层次，高考数学就到了120分以上。

4、巧。巧指的是你能从不同角度观察和分析同一道题，能够在多个解法之中选择最优解法。在限定时间内，能够准确审题，判断解法的优劣并顺利执行，的确需要相当的积累。

题海虽然无边，会总结的人能够上岸。要达到巧这个层次，给你三个建议：1。解综合题2。从一题多解，一解多题中总结题型和解法

5、通。武侠小说里讲的打通任督二脉，大约就是这样的状态吧。通的主要表现就是数学知识、数学方法、数学思想之间能够快速建立联系、无障碍切换。

明确自己所在的水平层次，选择相应的策略，一步一个脚印，踏踏实实攀登新的高峰。

三、怎么考？

厦门教育局副局长、数学特级教师任勇老师曾经给出过一个非常经典的“攻城锦囊”，值得众多考生借鉴和学习。

1、填写信息，稳定情绪；2、总览全卷，区别难易；

3、认真审题，灵活答题；4、过程清晰，稳中求快；

5、心理状态，注意调节；6、尽量多做，分分必争；

7、抓住“题眼” ，构建“桥梁”；8、遇到易题，格外小心；

9、思路暂塞，学会变通；10、注意检查，减少失误。

两个误区：

1、对于检查的认识。没时间检查，也检查不出来，所以必须一次作对！

2、试卷、答卷、草稿纸的使用。客观题尽量保留轨迹在一卷上，既节约草稿纸又便于回顾查看，避免信息转移出错。

笔者给出一个时间分配参考范例

在高三的复习过程，我们可以借助三问的哲学智慧，认识问题、分析问题、解决问题，从而突破一个个的目标和自我价值的实现.