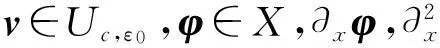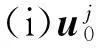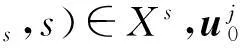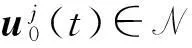非线性色散系统孤波解的轨道稳定性
刘小华, 胡丽金, 余孝军
(1. 贵州民族大学 理学院, 贵州 贵阳 550025; 2. 贵州财经大学 数学与统计学院, 贵州 贵阳 550025)
非线性色散系统孤波解的轨道稳定性
刘小华1,胡丽金1,余孝军2
(1. 贵州民族大学 理学院, 贵州 贵阳 550025;2. 贵州财经大学 数学与统计学院, 贵州 贵阳 550025)
摘要:利用变分法考虑非线性色散系统孤波解的存在性.借助轨道稳定性抽象理论,构造泛函极值问题和哈密尔顿算子,并对算子进行谱分析,证明非线性色散系统孤波解的轨道稳定性取决于判别式的符号,并推广了已有文献的一些结论.
关键词:孤波解; 轨道稳定性; 变分法
1引言及预备知识
本文将考虑非线性色散系统
(1)
孤波解的轨道稳定性,其中,u(x,t)、v(x,t)为是实函数,p为整数.方程(1)[1-2]描述的是分层流体学中邻近的密度跃层二维内部重力波的强交互作用,是浅水波KdV型方程的重要耦合形式.E. Alarcon等[1]研究了方程(1)以下几个问题:一是利用Kate理论[3]以及Lp-Lq估计法[4-5],证明了方程(1)初值问题的全局适定性;二是利用文献[6]的结论,给出了方程(1)孤波解的存在性;三是利用文献[7]的抽象轨道稳定性理论证明了方程(1)一种特殊孤波解的轨道稳定性.当p=2,以文献[8-9]的工作为基础,文献[10]建立了方程(1)孤波解的稳定性.还有许多作者[11-12]讨论了非线性方程解的其它特性.
方程(1)是广义KdV型耦合系统
(2)
的一种特殊情形,其中,f和g为光滑函数.文献[13]研究了系统(2)的一种特殊情况
ut-6uux+12vvx-uxxx=0,
ut+6uvx+2uxxx=0
的精确解.系统(2)中许多其它特殊情况的研究可以参见文献[14-16].
本文记号说明:设Hs(s≥1)为Sobolev空间,其范数为
傅里叶变换为
Lq=Lq(R)为通常的Lebesgue空间,其范数为|f|q(f∈Lq),记Xs=Hs×Hs(s≥1),积空间
是一个Banach空间,其范数为
记
f1=(f1,g1)T与f2=(f2,g2)T的内积
以及f1f2=(f1f2,g1g2).
2孤波解的存在性
方程(1)可以写为如下哈密尔顿形式
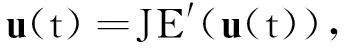
(3)
其中
(4)
E′为E的Frechet导数.在后面的讨论中,需要泛函
(5)
将孤波解φc(ξ)=(φ(ξ),ψ(ξ))T,ξ=x-ct代入方程(1),其中c为波速,并积分一次,那么φ(ξ)和ψ(ξ)满足方程
(6)
其中“′”为关于变量ξ的导数.根据(4)~(6)式,简单计算可知E′(φc)+Q′(φc)=0且E和Q守恒,Q′为Q的Frechet导数.在行波解φc处,定义
对(6)式的2个方程两边同时对ξ求导数,容易得知Hcφcx=0.
为讨论孤波解的存在性,引入2个泛函
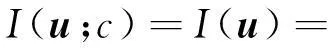
(8)

(9)
并且构造极小值问题
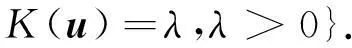
(10)
如果ψ=(ψ1,ψ2)T∈Xs满足问题(10),那么存在一个拉格朗日乘子μ使得
(11)
比较方程(6)和(11),并经过简单的计算可知φc(ξ)=μ-1/2pψ满足方程(6),因此,为了研究方程(6)孤波解φc(ξ)的存在性,转而讨论极小值问题(10)解的存在性.
由于(8)和(9)式以及泛函I和K具有齐次性,可以得知孤波解为如下问题(11)的解
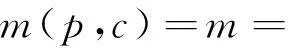
(12)
比较(10)和(12)式有
(13)
更进一步由(12)式知孤波解φc(ξ)适合
(14)
用φ乘以方程(6)的第一式两边,用ψ乘以方程(6)的第二式两边,然后对x从-∞到+∞积分可以得到
(15)

定理 2.2设c>0,ψk为极小化序列,则对于λ>0,存在子序列(仍记为ψk),yk∈R以及ψ∈Xs,使得ψk(·+yk)→ψ(k→∞),其中,ψ满足极值问题(10).
证明对于α∈(0,λ),由(13)式经简单计算得
由I(u)的定义(8)式可知其满足强制性条件
(16)

有界,因此存在收敛子序列,仍记为ρk,记
更进一步,当k充分大时,可以假设
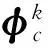
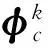
从而I(ψ)=Mλ.
由文献[1]可知,方程(1)存在以u(0)=u0为初值的全局解u(t)∈C([0,+∞,Xs),其中,s≥1.
定义 2.3[1]如果对于任意ε>0,存在δ>0,当
时,方程(1)的全局解u(·,t)满足
其中,u(·,0)=u0,则称轨道φc(·-y)是稳定的,否则称其不稳定.
接下来,将讨论孤波解φc的稳定性.
3孤波解的轨道稳定性
为了后文讨论孤波解的轨道稳定和不稳定性,给出Hc的假设如下.
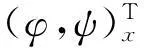
此证明见文献[1].
引理 3.2函数m在c>0内局部Lipschitz连续且关于c严格单调递增.
证明对于任意c1和c2,不失一般性设0 分别为速度c=c1和c=c2的有界态解,那么 因此,m关于c严格递增.另一方面 从而 根据(16)式知 综合这两式可得 这就证明了函数m在c>0内局部Lipschitz连续. 定义函数d(c)=E(φc)+cQ(φc),根据泛函E、I、Q、K的定义(4)和(5)以及(8)和(9)式易知 (17) 利用(15)式可得 (18) 在以下的讨论中,视d为c的函数,d′、d″分别为关于变量c的一阶、二阶导数,设管域为 引理 3.3设c>0,如果d″(c)>0,则存在ε>0,使得对于任意u∈Uc,ε有 证明由d′(c)=Q(φc)及Taylor公式有 其中,c1充分接近c,ε充分小,对于u∈Uc,ε可以得到 (19) 根据(18)式可得 加上φc(u)满足Mλ,从而 (20) 根据(19)和(20)式可得 因此,引理3.3成立. 定理 3.4设c>0,如果d″(c)>0,则方程(1)的孤波解φc是稳定的. 但由于un关于t的连续性,存在tn使得 (21) 根据泛函E和Q的连续性以及守恒性可知 (22) (23) 利用引理3.3可得 (24) 利用(21)式可知 而且 由(16)式成立 由于K、d的连续性、c(un(tn))的有界性以及 可得: (25) 利用(22)、(23)和(25)式容易知道 (26) 因此un(tn)为极小化序列,从而存在收敛子列收敛于φc,与(21)式矛盾. 4孤波解的不稳定性 引理 4.1存在ε0>0以及C1映射α:Uc,ε0→R,对于任意v∈Uc,ε0,r∈R使得: (i) 〈∂xφc(·-y),v〉=0; (ii)α(v(·-r))=α(v)+r; 证明参见文献[19]中的定理4.1.在后面的讨论中,将用到下面的新算子 (i) 映射Bφ:Uc,ε→Xs有界且具有有界导数; (ii)Bφ(v(·-r))=Bφ(v)+r; (iii) 对于任意v∈Uc,ε有 (iv) 如果〈φc,∂xφ)〉=0,则Bφ(φc)=Jφ. 证明(i) 根据算子Bφ的定义以及引理4.1中的(ii)容易知道(i)和(ii)成立. 由(4)和(5)式得(iii)成立.由于〈φc,∂xφ)〉=0以及算子Bφ的定义有 设L(u)=E(u)+cQ(u)有引理4.3成立. 引理 4.3设φ如引理4.2所示, 如果d″(c)<0,则φ切M于φc,且 (27) 证明根据函数d(c)的定义可知d′(c)=Q(φc).定义 因此 以及 利用隐函数定理,存在C2映射h=h(σ)且h(0)=c,那么 (28) 又 因此 也就是φ切M于φc,由于L″(φc)=Hc以及 (29) 下面分别来计算上式右端的每一项,即 利用(6)式和分部积分法有 (30) 利用(6)和(18)式及分部积分法有 (31) 对方程(6)两边同时关于c求导可得 (32) 因此 也就是 (33) 根据(28)式可知 即 (34) 综合(29)、(30)和(32)~(34)式以及d″(c)<0可得 引理 4.4假设φ如引理4.2所示,则J(φc)=0且 其中 证明参见文献[17]. 引理 4.5初值问题 v(0)=v0 存在C1解R(v0,s)满足:Q(R(v0,s))与s无关. 证明参见文献[7,19]. 引理 4.6假设φ如引理4.2所示,则存在ε、σ使得v0∈Uc,ε满足 其中,s∈(-σ,σ),P(v0)=〈L′(v0),Bφ(v0)〉. 证明假设 (35) 利用Taylor定理,容易得到 (36) 其中,θ∈(0,1).利用引理4.3和L′(φc)=0易得 因此 (37) 其中,s∈(-σ,σ).根据引理4.4知 以及 (38) 设 下面将证明 如果〈J′(φc),φc〉=0,则φ切N于φc,根据引理4.4有 因此 这结论与引理4.3矛盾.从而 综上可知,存在ε、σ,对于v0∈Uc,ε有函数s=s(v0)∈(-σ,σ)使得 (39) 利用(38)和(39)式可得 (40) 其中,s∈(-σ,σ). 证明在(40)式中利用R(φc,δ)=v0可得 (41) 其中,s,δ∈(-σ,σ).在上式中令s=-δ有 (42) 其中,δ∈(-σ,σ). 由于 以及(36)式可知映射δ→L(R(φc,δ)在δ=0处取得局部极大值,从而 (43) 由(42)和(43)式易得 (44) 设 根据引理4.6有 (45) 由于 (46) 其中,t∈[0,Tj].设 根据Cauchy-Schwarz不等式可得 同时利用引理4.1、4.2和引理4.6有 根据(46)式可得 因此 从而结论成立. 根据定理4.7,很容易得到以下定理. 定理 4.8设c>0,φc为方程(1)的孤波解,如果d″(c)<0,则φc轨道不稳定. 注 4.9文献[1]中的定理6.10可以直接从定理4.7和定理4.8中推导出来. 参考文献 [1] ALARCON E, ANGULO J, MOTENEGRO J. Stability and instability of solitary waves for a nonlinear dispersive system[J]. Nonlinear Anal,1999,36:1015-1034. [2] GEAR J, GRIMSHAW R. Weak and strong interactions between internal solitary waves[J]. Studies Appl Math,1984,70(3):235-258. [3] KATO T. On the cauchy problem for the generalized Korteweg-de Vries equation[J]. Adv Math Supplementary Studies,1983,8:93-128. [4] KENING C E, PONCE G, VEGA L. Oscillatory integrals and regularity of dispersive equation[J]. Indiana University Math J,1991,40:33-69. [5] KENING C E, PONCE G, VEGA L. Well-posedness of the initial value problem for the Korteweg-de Vries equation[J]. J Am Math Society,1991,4:323-347. [6] LOPES O. Radial symmetry of niminizrs for some translation and rotation invariant functionals[J]. J Diff Eqns,1996,124(2):378-388. [7] GRILLAKIS M, SHATAH J, STRAUSS W. Stability theory of solitary waves in the presence of symmetry I[J]. J Functional Anal,1987,74:160-197. [8] WEINSTEIN M. Solitary waves of nonlinear dispersive evolution equations wih critical power nonlinearities[J]. J Diff Eqns,1987,69:192-203. [9] BONA J, SOUGANIDIS P, STRAUSS W. Stability and instability of solitary waves of Korteweg-de Vries type equation[J]. Proceeding Royal Society London,1987,A411:395-412. [10] HAKKAEV S, KIRCHEV K. Stability of solitary waves for a nonlinear dispersive system in a critical case[J]. Nonlinear Anal,2007,67:2890-2899. [11] 张健,朱世辉. 关于一类非线性Schrödinger方程最佳爆破准则[J]. 四川师范大学学报(自然科学版),2014,37(5):754-760. [12] 马超,黎定仕. 一类非自治微分积分方程的全局指数稳定性[J]. 四川师范大学学报(自然科学版),2014,37(5):639-642. [13] HIROTA R, SATSUMA J. Soliton solutions of a coupled Korteweg-de Vries equation[J]. Phy Lett,1981,A85:407-408. [14] KUPERSHMIDT B A. A Coupled Korteweg-de Vries equation with dispersion[J]. J Phy Math General,1985,18:L571-L573. [15] ITO M. Symmeries and conservations laws of coupled nonlinear wave equation[J]. Phy Lett,1982,A91:335-338. [16] GUHA-ROY C, BAGCHI B, SINHA D K. Traveling wave solutions and the coupled Korteweg-de Vries equation[J]. J Math Phy,1986,27:2558-2560. [17] LEVANDOSKY S, LIU Y. Stability of solitary waves of a generalized Ostrovsky equation[J]. SIAM J Math Anal,2006,38(3):985-1011. [18] LIONS P L. The concentration-compactness principle in the calculus of vvariations: the locally compact case, part 1 and part 2[J]. Nonlinear Anal,1984,1(109/145):223-283. [19] ANGULO J, BONA J, LINARES F, et al. Scaling,stability and singularities for nonlinear dispersive wave equations: the crital case[J]. Nonlinearity,2002,15:759-786. 2010 MSC:39A24; 39A30 (编辑李德华) The Orbital Stability of the Solitary Solutions to the Nonlinear Dispersion System LIU Xiaohua1,HU Lijin1,YU Xiaojun2 (1.SchoolofScience,GuizhouMinzuUniversity,Guiyang550025,Guizhou;2.SchoolofMathematicalandStatistic,GuizhouUniversityofFinanceandEconomic,Guiyang550025,Guizhou) Abstract:In this paper, we investigate the existence of solitary wave solutions for the nonlinear dispersion system. By constructing the functional extremum problem and Hamilton operator, using spectral analysis and the orbital stability theory presented by Grillakis et al, we show that the solitary wave solutions of the the nonlinear dispersion system are orbitally stable or unstability as determined by the sign of a discriminant. The conclusions presented by the previous authors, such as Alarcon, Angulo and Motenegro, can be considered as special cases of our results. Key words:solitary wave solution; orbital stability; variational method doi:10.3969/j.issn.1001-8395.2016.01.009 中图分类号:O175.2 文献标志码:A 文章编号:1001-8395(2016)01-0051-08 作者简介:刘小华(1975—),女,教授,主要从事孤立子理论的研究,E-mail:lxhjkkl@yeah.net 基金项目:国家自然科学基金(71161005)、贵州省科学技术基金([2013]2138)、贵州省教育厅优秀科技创新人才支撑计划(KY[2012]092)和贵州省教育厅“数学建模及其应用创新人才团队”基金(黔教科研发[2013]405 号) 收稿日期:2014-06-27