基于复杂系统理论的公共危机预警方法研究

李 祥 飞， 阎 耀 军

(天津工业大学 公共危机管理研究所， 天津 300387)

基于复杂系统理论的公共危机预警方法研究

李 祥 飞， 阎 耀 军

(天津工业大学 公共危机管理研究所， 天津 300387)

公共危机的爆发往往具有演化、衍生等连锁反应，使得传统预警方法很难奏效。复杂系统分析为公共危机预警提供了新的思路。文章从复杂系统理论视角探讨了公共危机发生后可能导致的系统崩溃模式和机理，发现社会系统发生崩溃的方式与物理学中由于“熵”值增加导致的崩溃机理类似，可以借助“脆性熵”来衡量社会系统抵御公共危机事件冲击的能力。基于此，提出了结合系统风险解耦分析、智能等级评价、最大熵值计算以及支持向量机模型的预警方法，可以实现对公共危机事件危害范围的预警。

复杂系统；公共危机；预警

一、引 言

社会危机事件往往随着经济的快速发展变得越来越频发，其破坏力和破坏范围也有愈发加剧的趋势。从我国当前频频发生的危机事件来看，除了军事、政治面临的风险外，非传统意义上的金融安全、生态安全、资源安全等问题正变得日益突出，对整个社会系统的稳定产生了极大的负面影响[1]。传统的应对危机事件的方法是对危机事件的响应、处置、恢复、评估、重建、倡议和立法等。自中共中央2003年十六届三中全会提出要“建立健全社会预警体系及应急管理机制”以来，历时十余载我们已经建立起来涵盖自然灾害、事故灾难、社会安全、公共卫生等一系列公共危机的应急管理系统。但是反观危机事件的预警，我国的社会预警体系建设与庞大“应急管理”系统相比，仍然极为不对称[2][3]。这种“重应急，轻预警”的管理格局有管理体制、管理理念的原因，但是更深层次的原因在于技术层面无法产生突破，现有的对于社会稳定的风险研究多停留在社会指标评估方面，尚未有有效的危机预警工具。

值得注意的是，危机的发生往往具有较强的不确定性，其破坏作用的蔓延与演变也具有很强的不规律性，因此对于危机事件的预测就非常困难，传统的预测方法很难凑效[4][5] [6] [7]。从复杂系统的角度来看，我们的社会领域实际上是一个充满不确定性、非线性和难以认知的复杂系统，因此危机事件的直接作用对象是一个完整系统，一个危机事件的爆发很有可能发生系统性扩散甚至演变为新的危机事件，对整个社会系统造成大范围的影响。因此，即使不能及时预测危机事件的发生，如果能够对我们的社会系统抵御风险的能力进行评估和预测，则能够有效控制公共危机事件产生的影响范围，从而降低损失。

因此，本研究从危机的系统性蔓延视角，探讨危机扩散的机理，并在此基础上提出了运用支持向量机的预警方法，研究结果表明本文提出的方法能够有效对社会系统抵御风险的能力进行预判。

二、复杂系统崩溃机理

如果把危机在不同子系统之间的扩散看成是子系统之间发生崩溃，那么我们需要理清不同子系统之间可能发生崩溃的方式。其中复杂系统脆性概念的提出为研究子系统之间的崩溃方式提供了参考，其基本观点为：(1)在一个完整的系统中，不同子系统之间的联系中存在两种形式的熵，其中正熵代表的是系统的无序状态，其值越大则表明系统之间混乱程度越强，在受到外力干扰时发生崩溃的可能性就越大。负熵则可以抵消和中和正熵，因此可以降低这种无序状态。负熵的存在使得系统可以进行自我修正，当其存在的量不足以维持抵消正熵的增加时系统就容易发生崩溃。(2)负熵是可以在子系统之间流转的，当系统受到外来作用力干扰时会争夺负熵，因为负熵的有限性子系统之间会存在一种争夺负熵的非合作博弈的状态。(3)整个系统的崩溃是子系统之间发生崩溃蔓延所导致的，当系统受到外来作用力冲击时会使得子系统之间发生能量上的交换，进而导致正熵的值增加，当正熵的值超过临界时系统之间便会发生崩溃，而一个子系统的崩溃可能导致其他与之相邻的子系统也发生崩溃。

图1 子系统之间脆性熵的形式

通过对上面两种熵的描述可以发现：无论是热力学熵还是信息熵都是对某种无序状态的测量，热力学熵测量的是分子运动的无序，信息熵是用概率的形式对信息确定性程度进行测量，两种熵的表达方式非常类似。基于此我们可以将熵表示为对系统混乱程度的测量函数[9]。社会系统中子系统发生崩溃的可能性同样可以用熵来衡量，子系统之间的连接程度假设我们用“脆性”来测量，其程度越强则越容易发生系统之间的崩溃蔓延。此外还需要进一步分析一个危机系统的层次结构，从而能够衡量整个系统的脆弱程度。

三、公共危机的脆性解耦分析

1.系统风险的层次分析

构建整个系统的熵值是测量一个系统能够抵御危机事件能力的前提，为此需要深入分析一个系统可能的风险结构。首先一个风险系统可能由若干个相互关联的子系统组成，这种方式构成系统风险的内在部分，也就说系统的风险是以子系统之间发生风险为前提的。而每个子系统又由若干个危机事件组成，为了方便研究我们将其称为脆性事件，脆性事件可以影响到子系统的稳定[10]。脆性事件继续往下可以细分为若干脆性因子的集合，这些集合体之间以及不同层级之间是相互关联相互影响的。

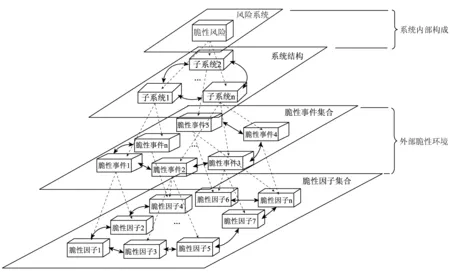
图2 系统风险的层次

如上图所示，一个系统的风险可以分解为若干层次，其中完整系统、子系统以及脆性事件包含的因素比较复杂，且具有不可定量性[11]。为此，我们将脆性事件继续细分，将能够反映其基本特征的具有稳定性的特征因子挖掘出来，这样就形成了若干个脆性因子的集合。值得注意的是不同的因子组合可能产生不同的脆性事件，以交通系统为例，车流量跟天气恶劣情况组合可能导致车祸事件发生，车流量跟人流量组合可能导致交通拥堵事件发生。在实际情况中因子的作用力是不同的，要根据实际情况确定其权重的大小。

2.脆性因子分类等级

如上面所提到的，系统之间发生崩溃蔓延的可能性大小可以用脆性程度的大小来表示，同样子系统细分之后的脆性事件以及脆性因子之间仍然可以用脆性代替其发生崩溃的可能程度。脆性程度主要有两个层面：对冲击的敏感度和受到冲击后的恢复力程度[10]。根据这两个标准我们可以对系统的脆性程度进行分等级量化，现有研究对脆性事件的等级量化最直接的办法是利用德尔菲法[10] [12]，但是该方法主观性较强，不利于客观地进行评价。为了避免主观因素对脆性等级评定结果造成的影响，本研究采用基于数据挖掘技术的支持向量机对各个危机事件的脆性因子进行等级判定。

支持向量机实际上是将某一向量xi按照一定的函数关系φ(x)投射到某一更高维的空间上去，并借助于此对函数关系进行回归。支持向量机的基本函数形式为[13]：

f(x)=w·φ(x)+b

(1)

其中φ(x)为投射以后的函数，w为系数，b为常量。为求最优，我们可以将以上函数形式进行转化，变为如下求最优解的形式：

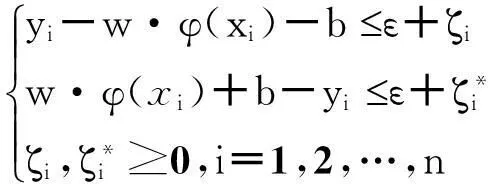
(2)

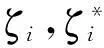
(3)

其中K(xi,xj)的表达形式可以是K(xi,xj)=φ(xi)φ(xj)，其代表的意思是支持向量机的核函数。核函数可以由不同的类型，本研究为了简化计算，选用了径向基核函数[14]，其表达形式如下：

(4)

(4)式中σ为径向基核函数的宽度参数。然而传统的网格搜索算法对于确定支持向量机参数仍有局限性，因此本文选用粒子群算法对支持向量机进行参数优化。利用支持向量机对风险系统进行脆性评级的基本运算流程如图3所示。

本研究提出的利用支持向量机对脆性因子进行等级分类的优势在于：首先，其在最大程度上减少了人为主观因素对评价带来的误差；其次，支持向量机可以有效地处理评价指标之间的非线性关系，使得数据的处理更加贴近现实；再次，支持向量机对于样本数据的要求相对不高，通过小样本的数据训练依旧能够获得较为精确的评价结果。最后，支持向量机可以通过自身的学习和自适应能力随着样本的扩大不断地进行自我调整，以适应不同阶段对于脆性等级评价的运算要求。

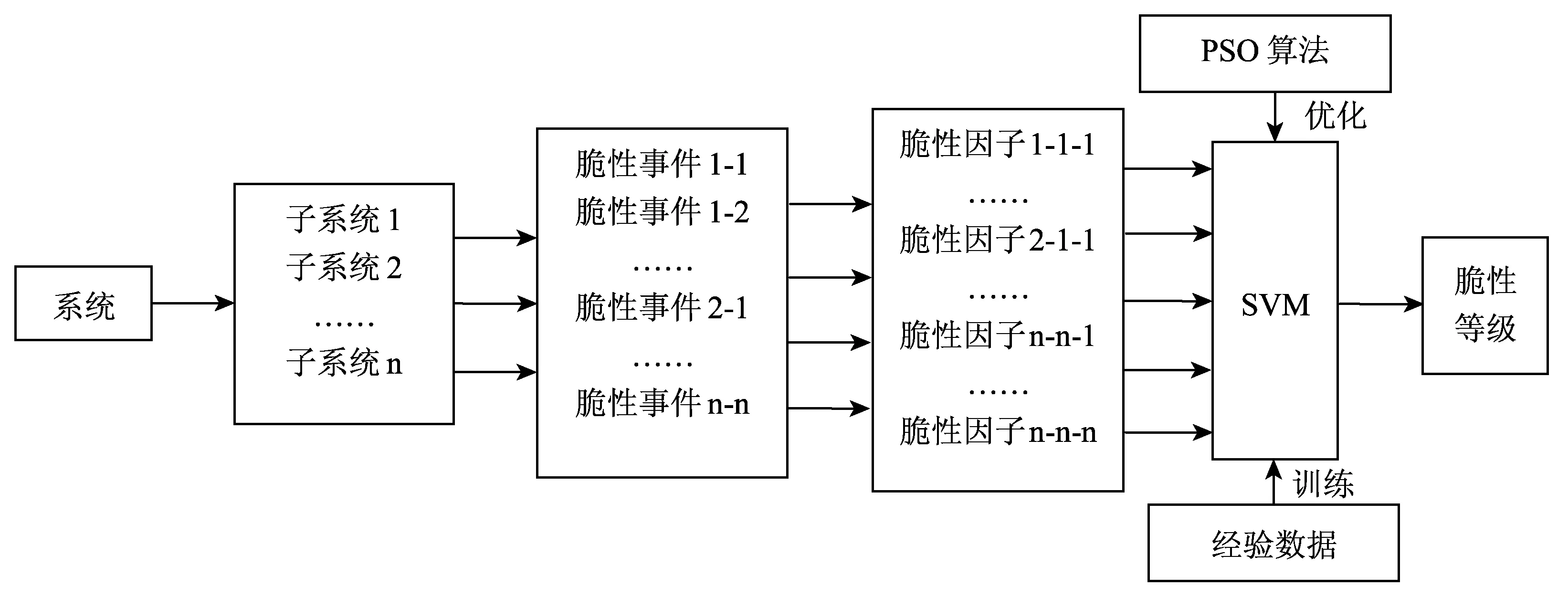
图3 基于支持向量机的公共系统脆性评价模型

3.系统脆性的定量化处理

根据图3对复杂系统的划定方式，系统风险最终可以划分为若干性质稳定的因子集合。根据最大熵值原理，各个因子一定存在一种分布使得可能产生的熵值最大[10]。而对于社会系统来说，熵值最大意味着系统内部的不确定性越大，即信息混乱的程度最大，系统可能发生崩溃的连锁反应越广泛。因此可以对最大熵值进行监测来实现预警社会系统抵御风险冲击的能力。

通过对以上系统风险的分析，可以将其设定为如下形式：u=g(u1,u2,…,ud)。其中ui为系统里不同的脆性因子集合，则由最大熵原理可以得到u的概率分布为：

G=max∫A[-f(u)lnf(u)]dx

(5)

其中A为随机变量的集合；在约束条件下，对系统的风险函数进行求解就变为求解条件极值。引入拉格朗日乘子，令：

(6)

此时问题转化为G*的极值问题，通过变分法可以得到：f(x)=exp(λ0+∑ui)。上式求解需要得到变量u的阶数以及脆性因子总数。令si为u的第i阶原点矩的观测值，脆性因子总数为n。信息构成约束条件为1，那么有：

∫Auif(u)dx=si,i=1,2,…,n

(7)

可以看出，要求得此脆性函数关系式需要确定参数λ0和λi。其中：

(8)

根据以上两式可以得到λ0和λi，因此可以得到脆性熵的函数关系式。这样就使得我们可以将各个因子的等级情况以及已知的历史数据作为输入而获得可以用来衡量完整系统脆性程度的熵值，通过对熵值的大小进行监测和预警就可以实现对社会系统风险性的预测和控制。

四、系统的脆性熵监测

根据以上数据处理可以得到关于系统最大风险熵的计算公式，它是关于脆性因子的函数关系式，根据脆性因子数据可以得到该最大熵的值。但是对于最大熵的计算只能是在已知各个脆性因子历史数据基础上才能得到，也就是说只能由事后统计各脆性因子的得分后才能计算出熵值，因此对于预测预警没有太大的意义。因此，本研究提出基于支持向量机模型的系统风险熵预测方法，这种预测方式考虑以时间作为横向维度，便于在各脆性因子尚不知道的情况下对未来情况进行预判。

1.样本选取

样本的选取以数据量大和易获取为主要原则，本研究以交通拥堵现象作为研究对象，将其视为一个完整的系统，当发生拥堵则视为危机产生。本研究选取一个十字路口40个时间点的交通事故作为安全系统样本，为了便于计算，本文只选取三个固定的脆性因子作为研究对象，分别为车流量/天(y1)、人流量/天(y2)、雨雪天气/天(y3)。其中每个时间点代表的数值以及通过SVM进行评价后得到的等级情况如下所示：

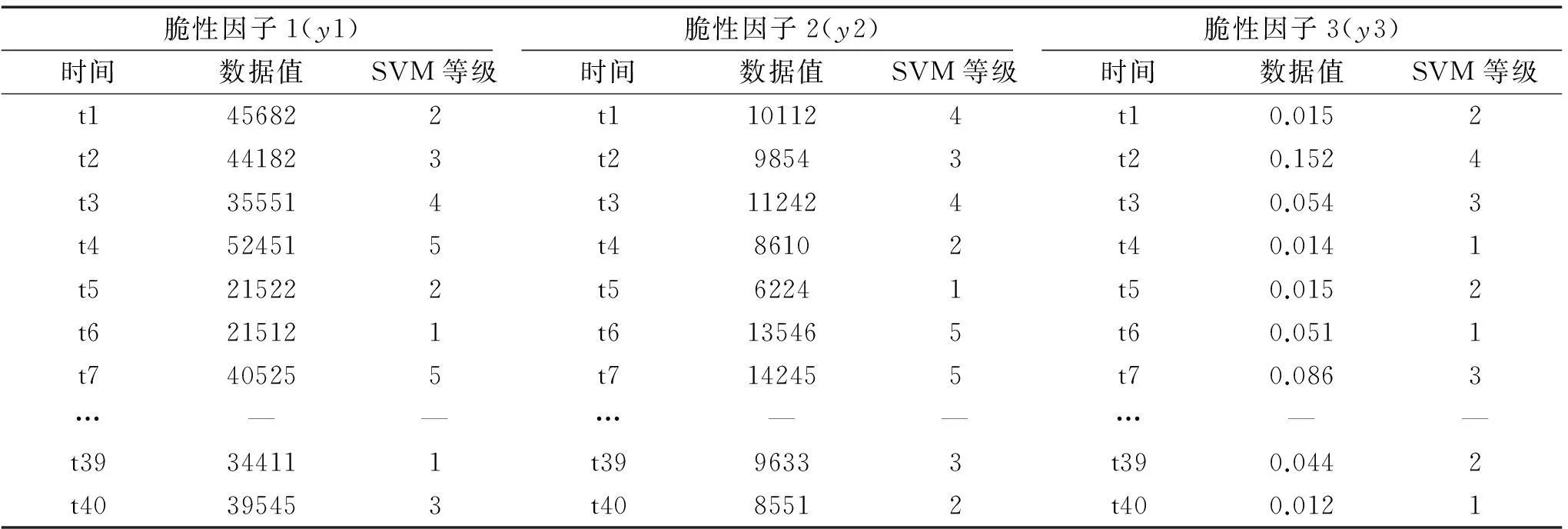
表1 脆性熵的指标数据与测评等级

注：等级从1级至5级表示脆性程度递增。以上为部分数据情况。

2.数据计算

利用支持向量机得到的各个因子的脆性等级，结合各因子的历史数据和概率分布形式可以计算得到样本系统的最大熵曲线如下：

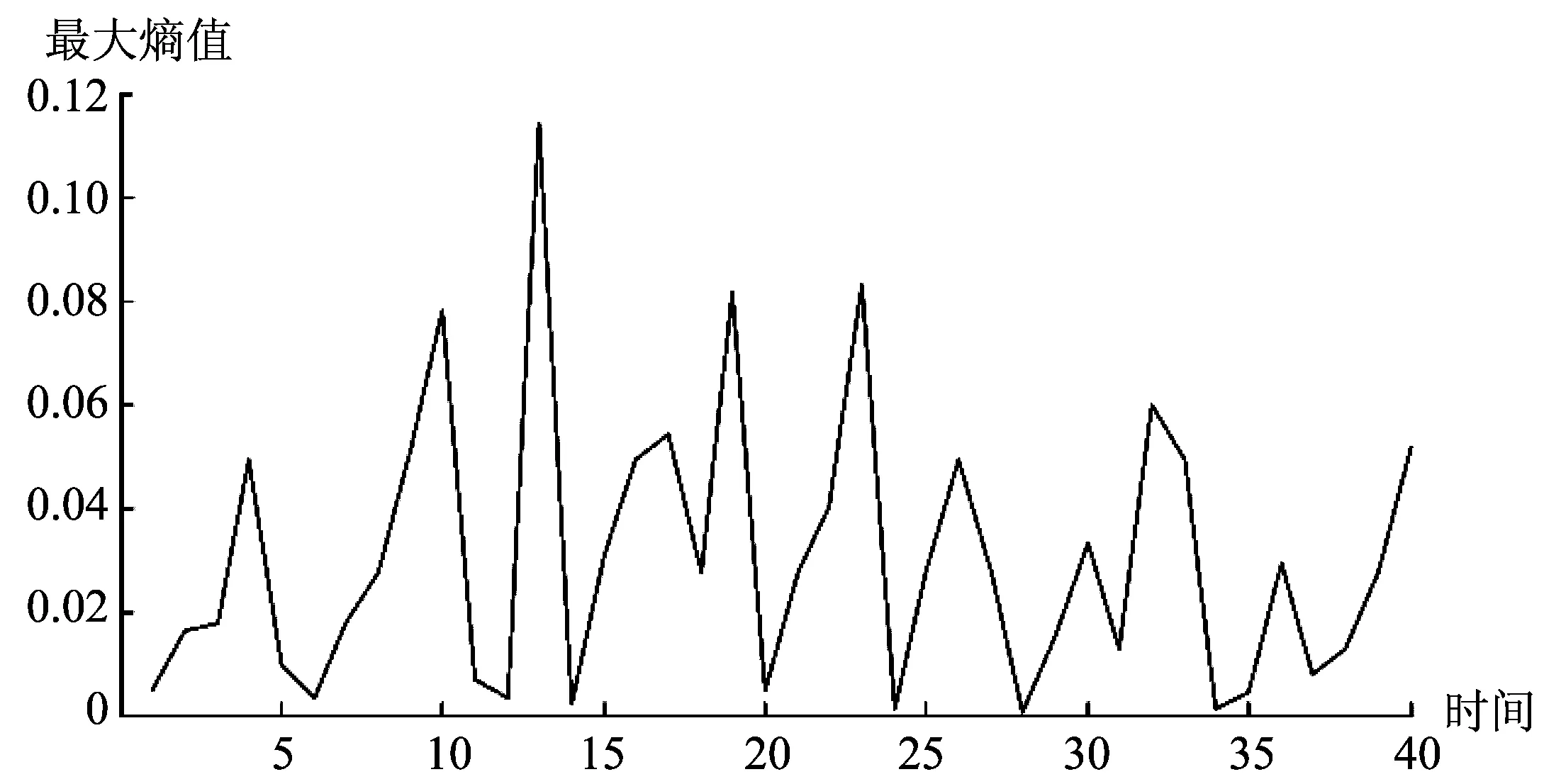
图4 最大熵值曲线时间序列图

如上图所示，熵值集合按照时间维度划分可以得到一个时间序列。本文尝试采用支持向量机对该时间序列进行预测。预测的算法选用Matlab7.0语言编程。基本的运算思路为将以上时间序列的采样值转化为一个矩阵(Xt,Yt)，其中Xt={xt-n,xt-n+1,….xt-1}，Yt=xt。其中n代表了运用前n个样本的值进行数据学习训练来预测第n+1个值的大小[15]。预测的结果如图5所示。对于选取的40个时间节点样本，本研究首先运用前25个样本作为学习进行训练，后15个样本检验预测效果。

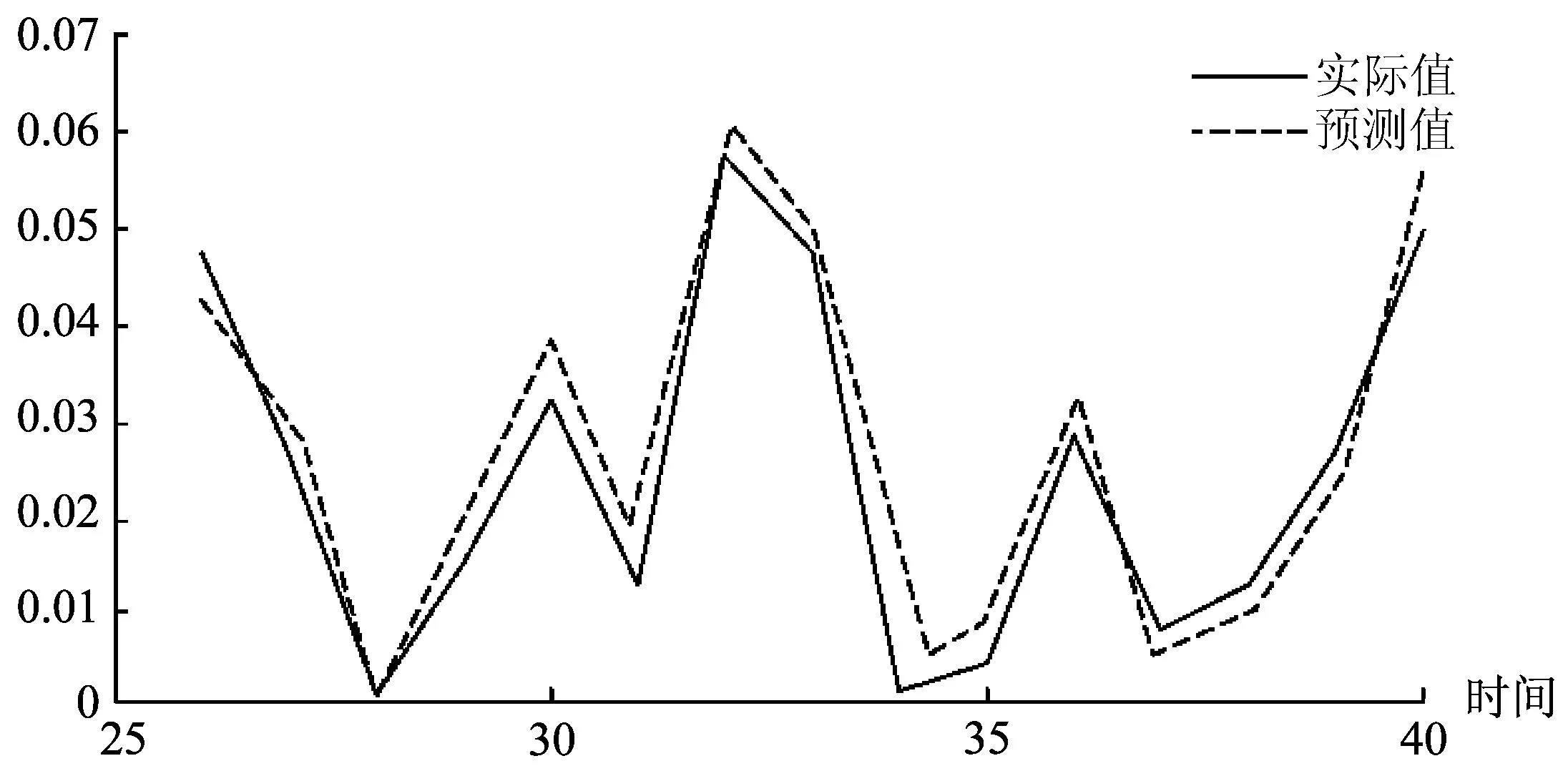
图5 基于支持向量机的脆性熵预测结果

在进行数据训练时对模型采用时间窗滚动，即将本点的实际数据视为已知的数据滚入训练样本集，去除时间最远点，重置训练后得到下一步的预测值。通过对前25个时间序列的训练得到支持向量机模型，如图5所示，比较最大熵值序列的实际值与预测值，用均方误差RSME和绝对百分比误差MAPE对预测精度进行衡量，其中RSME= 0.00169，MAPE=0.0422，均稳定在较低的水平。通过比较历史数据发现，当熵值较大时交通事故发生的起数，事故的严重程度更强。这表明支持向量机能够有效运用于对社会系统的最大熵值预测中。

五、结 语

本研究以系统论为基础，从复杂系统的脆性特性出发，探讨了公共危机事件的冲击对于社会稳定系统可能造成的影响以及危机发生扩散的可能方式，并尝试提出了一种新型公共危机预警方法。通过分析复杂系统受到冲击后不同子系统之间发生崩溃的机理，本研究认为社会稳定系统发生崩溃的方式与物理学中由“熵”值增加导致的系统崩溃机理类似，基于此提出了以“脆性熵”作为衡量社会系统抵御公共危机事件的冲击能力的标准。在脆性熵的评价上，本研究引入了基于数据挖掘技术的支持向量机模型，提高了评价的客观性和精确性。在系统脆性最大熵的测量上，本研究基于最大熵原理，将危机事件的历史数据和脆性熵评价相结合从而给出了函数计算方式。为了实现对公共危机事件危害范围的预警，文章最后提出了基于支持向量机模型的预警方法并以交通事件为例进行了实证分析，结果发现本研究提出的方法预测精度和可信度较高，具有良好的危机预警应用前景。

值得注意的是，本研究提出的预警方法是建立在对充足历史数据的分析基础上的，对于样本的要求较高，所以本研究仅以交通拥堵情况作为实证分析对象，缺乏一定的泛化性。因此选取更多类型的公共危机事件进行解耦、测量最大熵值并进行监控预测是未来研究的重要方向。

[1]刘霞. 公共危机治理：理论建构与战略重点[J]. 中国行政管理，2012,(3):116-120.

[2]阎耀军. 我国社会预警体系建设的纠结及其破解[J]. 国家行政学院学报，2012,(4):89-93.

[3]阎耀军，刘国富. 应急管理的前馈控制模式研究[J]. 中国应急管理，2010,(9):29-32.

[4]王娇俐，王文平，沈秋英. 基于风险传播机制的集群抗风险能力研究[J]. 大连理工大学学报(社会科学版)，2012,(01):60-64.

[5]VERHOEVEN P. Crisis? What crisis? How European professionals handle crises and crisis communication[J]. Public Relations Revies, 2013,(01):107-109.

[6]JIN Y. Examining publics’ crisis responses according to different shades of anger and sympathy[J]. Journal of Public Relations Research, 2014,(01):79-101.

[7]于丽英，蒋宗彩. 基于复杂系统观的城市群公共危机形成机制研究[J]. 系统科学学报，2013,(03):62-65.

[8]韦琦. 复杂系统崩溃的脆性致因研究[J]. 系统工程，2003,21(4):1-5.

[9]韦琦，金鸿章，郭健.基于脆性联系熵的复杂系统崩溃致因研究 [J]. 自动化技术与应用，2003,(4):1-4.

[10]金鸿章，李琦，吴红梅. 基于脆性因子的复杂系统脆性分析 [J]. 哈尔滨工程大学学报，2005,(12):739-743.

[11]COOMBS W T. How publics react to crisis communication efforts: comparing crisis response reactions across sub-arenas[J]. Journal of Communication Management,2014,(01):40-57.

[12]田军. 基于德尔菲法的专家集成模型研究[J]. 系统工程理论与实践，2004,(01):62-69.

[13]VAPNIK V．The Nature of Statistical Learning Theory[M]. New York:Springer-verlag,1999.121-163.

[14]张水波，康飞，李祥飞. 基于支持向量机的建设工程项目经理胜任力评价[J]. 中国软科学，2013,(11):89-89.

[15]李祥飞，张再生. 基于误差同步预测的SVM金融事件序列方法[J]. 天津大学学报(自然科学与工程技术版)，2014,(01):86-94.

Study of Public Crisis Warning Method Based on Complex System Theory

LI Xiangfei， YAN Yaojun

( Institution of Crisis Management, Tianjin Polytechnic University, Tianjin 300387, China )

The outbreak of public crisis tends to be evolutionary, derivative and easily formed to a chain reaction, which makes traditional early warning methods hardly work. However, complex system analysis provides a new way of thinking for public crisis warning. The modes and mechanisms of public crisis leading to system collapse were discussed in this paper. It was found that the social system collapses caused by public crisis events are similar to the collapse mechanisms caused by entropy value increase in physics studies. The abilities of social system can be measured to resist the impact of public crisis events, using “brittle entropy”. A hybrid warning method by integrating system risk decoupling, intelligent assessment, maximum entropy calculation analysis and support vector machine model was proposed, which can be used to forewarn the possible breakage degree caused by public crisis events.

complex system; public crisis; early warning

2015-07-02;

2015-08-19

国家社会科学基金重点项目：“基于政策模拟方法的社会稳定风险研究” (13ASH003)

李祥飞(1986- )，男，山东潍坊人，讲师，博士， 主要从事公共管理研究，E-mail：soar.li@163.com；阎耀军(1954-)，男，河北南宫人，教授， 主要从事社会预测与预警、预控与公共管理研究。

C93-05

A

1008-407X(2016)01-00104-06