基于周期FRFT的对称三角LFMCW信号检测算法

宦爱奇，刘　锋，王泽众

(1.海军航空工程学院，山东 烟台　264001； 2.海军装备研究院，北京　100249)



基于周期FRFT的对称三角LFMCW信号检测算法

宦爱奇1，刘锋1，王泽众2

(1.海军航空工程学院，山东 烟台264001； 2.海军装备研究院，北京100249)

摘要：对称三角线性调频连续波信号(STLFMCW)是一种常用的线性调频连续波信号，具有低截获概率性质。针对这一性质，提出了一种周期分数阶傅里叶变换(PFRFT)对对称三角线性调频连续波信号的检测算法；分析了对称三角线性调频连续波信号的PFRFT及其性质，并对无先验知识条件下的STLFMCW信号检测技术进行研究，给出了基于PFRFT的STLFMCW信号检测流程并进行性能分析仿真；仿真结果表明：该算法对STLFMCW信号有良好的检测性能，相比于FRFT，PFRFT更适合对STLFMCW信号进行处理。

关键词：周期分数阶傅里叶变换(PFRFT)；对称三角线性调频连续波(LFMCW)；信号检测

Citation format:HUAN Ai-qi, Liu Feng, WANG Ze-zhong.Symmetrical Triangular Linear Frequency Modulation Continuous Wave Radar Signal Detection Algorithm Based on Periodic Fourier Transform[J].Journal of Ordnance Equipment Engineering,2016(3):86-89.

低截获概率( LPI) 雷达信号具有波形复杂、 功率低、带宽宽等特点,雷达侦察接收机很难对其进行可靠识别[1]。对称三角线性调频连续波信号是低截获概率雷达普遍采用的信号形式之一。在雷达侦察中，如何对这类信号进行快速有效识别已成为一大难点，也是近几年电子侦查方向研究的一大热点[2]。

目前，已有多种信号处理方法可用于STLFMCW信号的检测与参数估计。文献[3]采用Winger Ville分布，Choi-Williams分布，循环平稳分析和QMFB的方法，文献[4]采用基于Wigner-Hough变换的STLFMCW信号特征提取算法，文献[5]提出一种高阶累积量技术与QMFB相结合的检测方法，文献[6]采用基于Radon-Ambiguity变换和分数阶傅里叶变换(FRFT)的信号检测与参数估计方法。然而Winger Ville分布由于受交叉项的影响，在信噪比较低的情况下难以提取信号特征；Choi-Williams分布虽然受交叉项影响较小，但是由于其能量聚集不集中，检测能力有明显减弱；由于QMFB本身没有抑制噪声的能力，其检测能力依赖于信号的消噪情况。Wigner-Hough变换和Radon-Wigner变换会被交叉项干扰且运量较大，实现 STLFMCW 信号的检测与参数估计需要大量时间[7-12]。分数阶Fourier变换作为一种线性变换，非常适合处理LFM信号，通过FFT快速算法大大减小计算复杂程度，然而由于其能量谱存在交叉项的干扰，在多分量情况下，进行信号检测与估计时出现虚假信号概率显著增加[13]。针对这一情况，本文采用基于周期FRFT的STLFMCW信号参数估计和检测方法，这一方法可对LFMCW信号的能量谱进行周期积累，从而解决交叉项问题并有效估计STLFMCW信号的特征参数。

1周期分数阶Fourier变换

连续函数x(t)的分数阶傅里叶变换(FRFT)定义如下[14]：

(1)

其中Kα(t,u)为FRFT的核函数，其表达式为

由于FRFT在分数阶傅里叶域(FRFD)内无法聚集成单个能量脉冲，为解决能量谱受交叉项影响问题，引入周期FRFT变换(PFRFT)概念，将FRFT的核函数Kα(t,u)进行周期调制，PFRFT的定义如下：

(2)

其核函数Kα,τ,T(t,u)为

mod(·)为取模算子，T为调制周期，τ为时间延迟。相比FRFT的核函数Kα(t,u)，PFRFT的核函数Kα,τ,T(t,u)调频率通过了周期调制。

每个周期内STLFMCW信号包含正、负调频率两部分LFM信号[6]，对其周期调制后，分别表示为

(3)

其时频特征如图1所示：

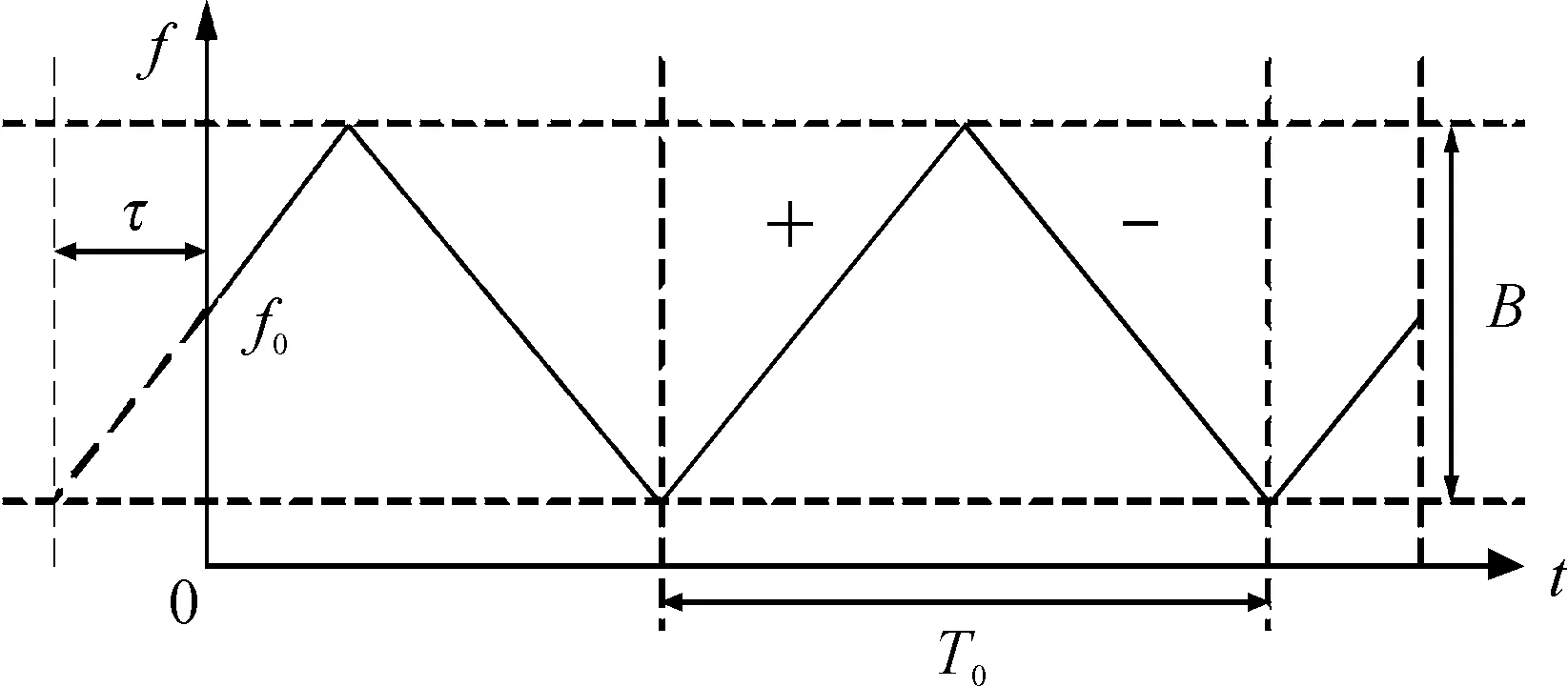
图1　STLFMCW信号的时频特征

设{P}为PFRFT的算子，STLFMCW信号的PFRFT可表示为

(4)

(5)

一个调制周期内的STLFMCW信号在PFRFT域的能量分布如图2所示。

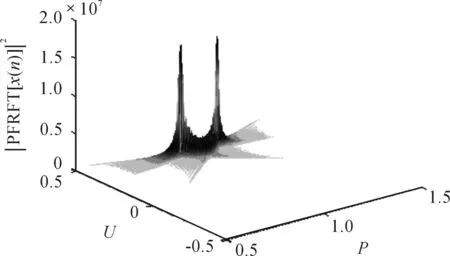
图2　STLFMCW的PFRFT能量分布特征

2周期FRFT域STLFMCW信号检测与参数估计算法

在雷达信号先验知识未知的情况下，信号检测问题可以采用统计学办法，用门限检测的方法对STLFMCW信号处理。通过设置门限，将检测输出区间设为信号区和噪声区，信号检测问题即成为二元假设检验问题。

设待检测信号s(n)为STLFMCW信号，则二元假设检验问题可以表示为：

其中：n(n)为噪声，s(n)为与噪声独立的STLFMCW信号，n=1,2,…,N，N表示采样点的数量。

为获取先验概率与代价因子，本文采用纽曼-皮尔逊准则设计检测器，从而在虚警概率Pfa确定的情况下，令检测概率Pd取得最大值。在周期FRFT域内，其检验统计量I为

(6)

则虚警概率Pfa为

(7)

检测概率为Pd为

(8)

在确定虚警概率Pfa和周期FRFT域H0假设下概率密度函数p(I|H0)的情况下，门限γ可以通过式(7)解算获得。将H1假设下I的概率密度函数p(I|H1)与获得的门限γ代入式(8)，使得检测概率为Pd最大，即最佳检测系统的检测概率Pd。

3检测与参数估计流程

从上述分析可知，STLFMCW信号可以认为是由两个LFMCW信号组成，在加性高斯白噪声中，雷达侦察接收机基于周期FRFT的STLFMCW信号检测与特征参数估计流程如图3所示。

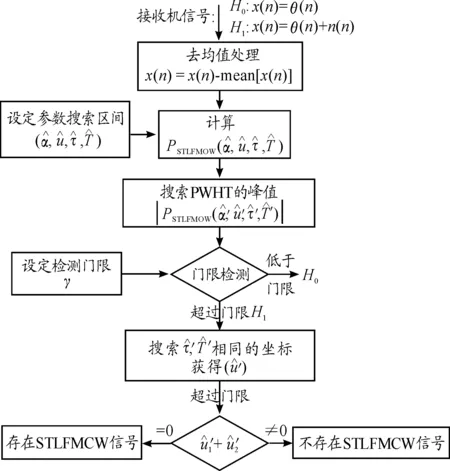
图3　检测与参数估计流程

具体流程描述：

步骤1：对输入信号x(n)做均值化处理：x′(n)=x(n)-mean[x(n)]。其中mean[·]为均值算子。

步骤2：由雷达侦察接收机的内部噪声的统计特征(本文中为等效高斯白)、采样点数N(由采样频率fs和观测时间Tobs决定，N=Tobs·fs)，得到在周期FRFT域内部噪声的概率密度函数p(I|H0)。由概率密度函数和要求的虚警概率Pfa，确定STLFMCW信号的检测门限γ；

4检测与估计性能分析仿真

为验证基于PFRFT的STLFMCW信号检测性能，本文采用Monte Carlo法，假设背景为在高斯白噪声条件下，虚警概率Pfa=0.01，做1 000次Monte Carlo仿真。图4为信号检测概率与SNR之间的关系。

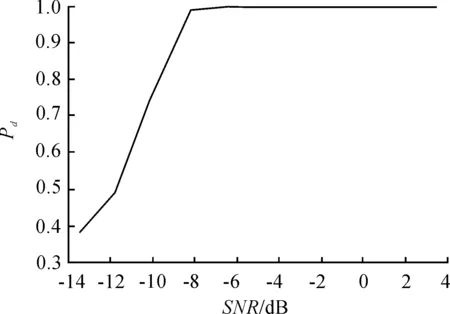
图4　信号检测概率与信噪比关系

从图4可知，对于STLFMCW信号，当输入信噪比在-8 dB以上时，周期FRFT算法具有良好的检测性能，检测概率高于0.9。

为检验FRFT算法与PFRFT算法对STLFMCW信号检测的优劣性，分别采用FRFT和PFRFT算法对高斯白噪声条件下的STLFMCW信号进行检测与参数估计，假设参数估计相对误差不超过5%，采用Monte Carlo法对信噪比为-15 dB，-7 dB进行仿真，STLFMCW信号的FRFT和PFRFT的ROC曲线如图5所示。

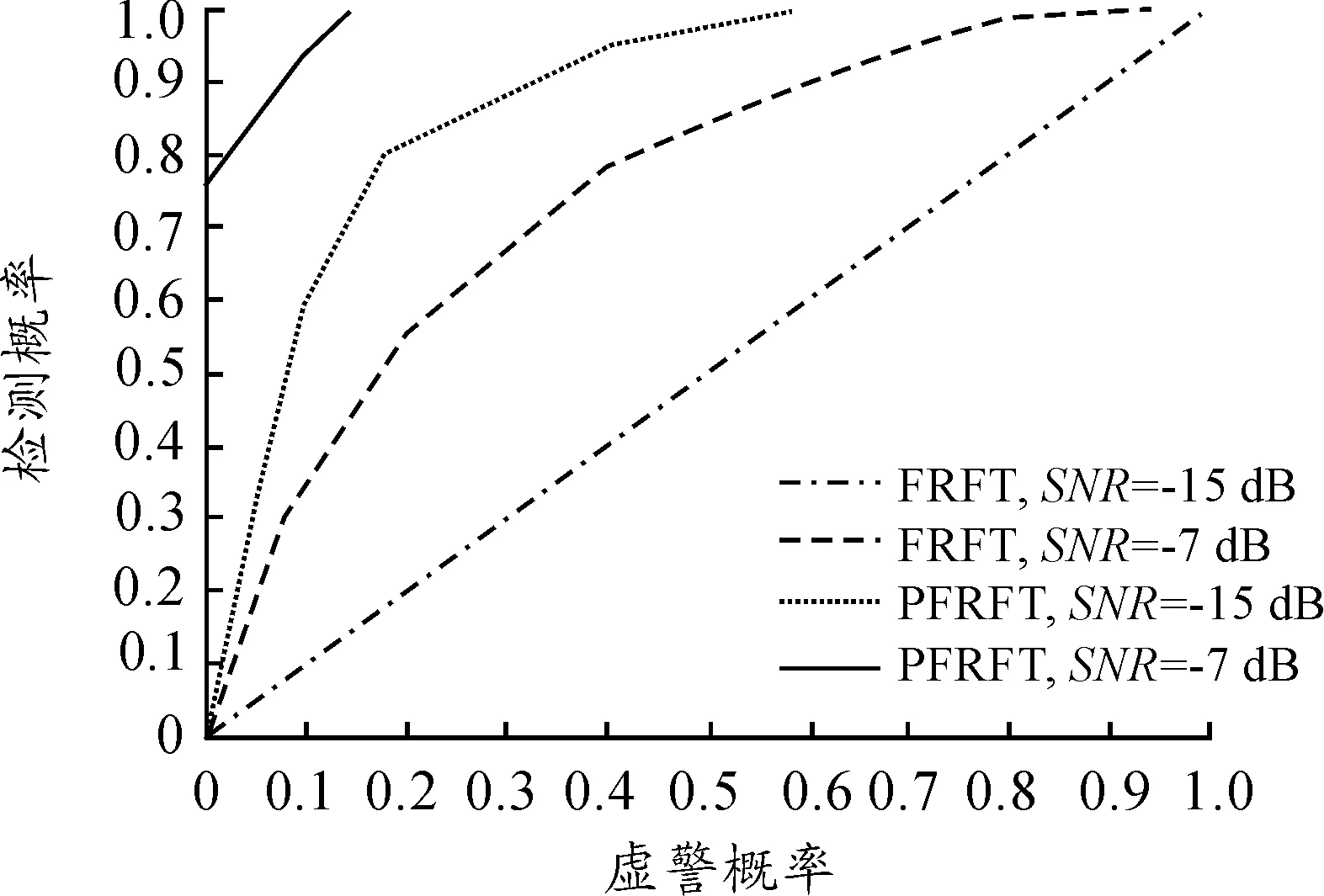
图5　FRFT与PFRFT检测性能ROC曲线

从图5 ROC曲线可以看出无论输入信噪比为-7 dB还是-15 dB，PFRFT对STLFMCW的检测效果都明显好于FRFT。仿真验证了基于周期FRFT的STLFMCW信号检测算法的良好检测能力。

5结论

本文提出一种基于周期FRFT的STLFMCW信号的检测与参数估计算法，给出了检测与参数估计算法的实现流程，并对周期FRFT域的STLFMCW信号的检测性能进行了仿真验证。仿真结果表明，随着信噪比的增长，基于PFRFT的STLFMCW信号检测算法的检测性能增长；与FRFT相比，PFRFT在相同信噪比情况下，有更加良好的检测性能。相较于基于FRFT的检测算法，该算法在低信噪比情况下对STLFMCW信号检测能力更有效，具有一定的实际应用价值和理论研究价值。

参考文献：

[1]WIRTH W.Polyphase coded CW radar[C]//Proceedings of the IEEE Fourth International Symposium on Spread Spectrum Techniques and Applications.Mainz,1996:186-190.

[2]徐会法.基于FrFT的一类低截获概率雷达信号截获与识别研究 [D].烟台:海军航空工程学院,2011.

[3]PACE P E.Detection and Classifying Low Probability of Intercept Rader[M].Second Edition,Boston:Artech House,2009:81-119,405-547.

[4]LIU FENG,XU HUI-FA,SUN DA-PENG.Feature extraction of symmetrical triangular LFMCW signal using Wigner-Hough transform[J].Journal of Beijing Institute of Technology,2009,18(4):478 - 483.

[5]戴幻尧,蒋鸿宇.基于滤波器组和高阶累积量技术的LPI 信号特征检测的新方法[J].系统工程与电子技术,2009,31(6):1336- 1340.

[6]袁伟明,王敏,吴顺君.对称三角线性调频连续波信号的检测与参数估计[J].电波科学学报,2005,20(5):594 - 597.

[7]赵兴浩,邓兵,陶然.分数阶傅立叶变换数值计算中的量纲归一化[J].北京理工大学学报,2005,25(4):360 - 364.

[8]BARBAROSSA S,SCAGLIONE A,SPALLETTA A.Adaptive suppression of wideband interferences in spread-spectrum communications using the Wigner-Hough transforms [J].IEEE International Conference on Acoustics,Speech,and Signal Processing,1997(5):3861-3854.

[9]孙晓昶,皇甫堪.基于Wigner-Hough变换的多分量LFM信号检测及离散计算方法[J].电子学报.2003,31(2):1-4.

[10]梁红,胡旭娟,朱云周.基于RSPWVD-Hough的多分量LFM信号检测[J].系统仿真学报.2007,13:3030-3032.

[11]夏云龙,朴胜春,付永庆.一种基于时间反转镜和Wigner-Hough变换的线性调频信号检测方法[J].中南大学学报(自然科学版)，2009,40(3):719-724.

[12]刘锋,孙大鹏,黄宇等.基于改进Wigner-Hough变换的多分量LFM信号特征提取[J].北京理工大学学报,2008,28(10):914-917.

[13]GEROLEO F G,PEARCE M B.Detection and Estimation of Multi-Pulse LFMCW Radar Signals[C]//2010 IEEE International Radar Conference.2010:1009-1013.

[14]陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009:39-45.

(责任编辑杨继森)

Symmetrical Triangular Linear Frequency Modulation Continuous Wave Radar Signal Detection Algorithm Based on Periodic Fourier Transform

HUAN Ai-qi1, Liu Feng1, WANG Ze-zhong2

(1.Naval Aeronautical Engineering Institute, Yantai 264001, China；2.Naval Armament Research Institute, Beijing 100249, China)

Abstract:Symmetrical triangular linear frequency modulation continuous wave(STLFMCW) radar signal which has low probability interception characteristics is a common linear frequency modulation continuous wave radar signal. For this characteristic, a STLFMCW detection algorithm which was based on periodic Fourier transform(PFRFT) was proposed. Firstly, the properties of the periodic FRFT of symmetrical triangular linearly frequency modulated continuous wave signals were analyzed. Secondly, STLFMCW signals detection technology with no prior knowledge was studied. Finally, the workflow of the application of the algorithm and simulations of STLFMCW based on PFRFT were proposed. The simulations verify the good detection performance of the algorithm. Compared to FRFT, PFRFT is more suitable for processing STLFMCW signals.

Key words:PFRFT; STLFMCW; signal detection

文章编号：1006-0707(2016)03-0086-04

中图分类号：TN957

文献标识码：A

doi:10.11809/scbgxb2016.03.021

作者简介：宦爱奇(1991—)，男，硕士研究生，主要从事雷达侦察信号处理研究。

基金项目：国家自然科学基金(61571454)

收稿日期：2015-08-23；修回日期：2015-09-27

本文引用格式：宦爱奇，刘锋，王泽众.基于周期FRFT的对称三角LFMCW信号检测算法[J].兵器装备工程学报，2016(3):86-89.

【信息科学与控制工程】