混凝土箱梁桥的负温差及其效应分析

汪 剑,万 俊

（武汉市政工程设计研究院有限责任公司，湖北 武汉 430015）

混凝土箱梁桥的负温差及其效应分析

汪 剑,万 俊

（武汉市政工程设计研究院有限责任公司，湖北 武汉 430015）

运用辐射换热、对流换热等相关理论，对箱梁表面的各种热流进行分析，并将各种热流转换成易于加载的对流换热形式，即采用综合对流换热系数和综合大气温度来反映箱梁表面各种热流，在此基础上应用有限元方法对箱梁温度场进行计算，获得了箱梁在降温作用下箱梁温度场的分布规律，与现有规范中的负温差模式进行对比，为箱梁负温度梯度模式的合理确定提供了可靠依据。最后采用空间有限元程序分析了混凝土箱梁桥在骤然降温作用下的效应，为同类型箱梁桥的设计提供参考。

混凝土箱梁；降温温差；对流换热；有限元；温度场；温度效应

0 引言

置于自然环境中的桥梁结构，其内外表面处于一个十分复杂的换热过程中，由此造成桥梁结构的温度分布也是十分复杂的[1-2]。但就混凝土薄壁箱形截面梁而言，其换热形式大致可分为三种：（1）箱形梁表面吸收的热辐射和箱形梁向外界发出的热辐射；（2）箱形梁表面与周围空气发生的对流热交换；（3）箱形梁混凝土内部发生的热传导。

本文采用ANSYS计算了箱梁在降温作用下的箱梁瞬态温度场，获得了混凝土箱梁在降温作用下箱梁温度场的一般规律，为箱梁负温度梯度模式的合理确定提供了可靠依据。并在此基础上采用ANSYS对混凝土箱梁在负温差模式下产生的效应进行分析，为同类箱梁桥设计提供参考。

1 箱梁表面热流分析

对于任意无内热源平面不稳定温度场，其有限元计算的基本微分方程为[1,3]

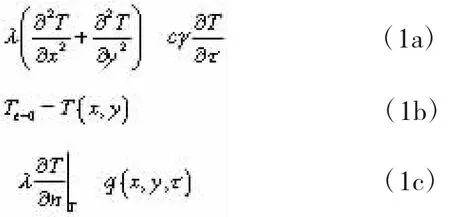
式中：式（1a）为傅里叶导热微分方程，式（1b）为初始条件，式（1c）为第二类边界条件（诺伊曼条件），其中q（x，y，τ）为已知的边界上的热流密度函数，式中其他参数意义详见文献[3]。因此要对混凝土箱梁进行温度场有限元分析，首先必须对其表面进行详细的热流分析。

混凝土箱梁外表面除与空气发生热量的传递外，还会受到辐射换热的作用，其中包括太阳直射辐射、天空散射辐射、地面反射辐射以及大气长波辐射和来自地面的长波辐射，当这些因素同时对混凝土箱梁的外表面产生影响时，其外表面的热平衡可用下式表示

式中：qs为箱梁外表面所吸收的太阳辐射热量；qR为箱梁外表面所吸收的地面反射辐射热量；qB为箱梁外表面所吸收的大气长波辐射热量；qg为箱梁外表面所吸收的地面热辐射；q0为箱梁外表面向壁体内侧传热量；qca为箱梁外表面向周围空气进行的对流换热量；qra为箱梁外表面向周围环境发出的热辐射。对于上述换热量，qs和qR的计算已有较多文献涉及[2-3]，在此不再详述。

此外为方便计算，将上述三种形式的热流均转换成对流换热，即将式（1）中的第二类边界条件转换成第三类边界条件（罗宾条件）：

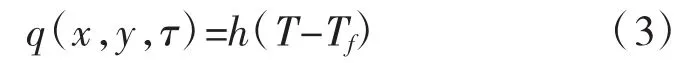
式中：Tf为流体温度；h为换热系数。即由一个综合对流换热系数和一个综合大气温度来表示各种热量。

1.1 综合对流换热系数ha的计算

箱梁外表面的对流换热系数和辐射换热系数，均与外界气象条件（风速、箱梁周围环境温度、天空温度等）以及外表面的温度有关，因此它们实际上都是变量，但为了计算工作的简便，一般采用一个总换热系数ha来统一计算表面对外（包括对流和辐射两部分）的总换热量（包括qca和qra）[2]。

对于辐射换热，根据基尔霍夫定律，混凝土箱梁外表面与外界的辐射换热量qra为[2]

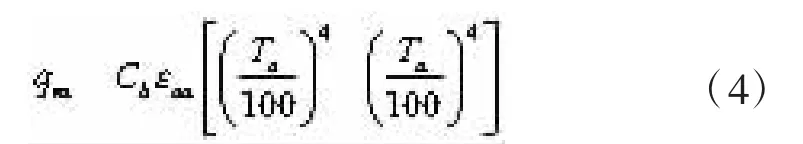
式中：Cb为黑体的辐射常数；εoa为箱梁外表面与天空辐射面间的辐射系统黑度（系统黑度基本上等于混凝土表面黑度εo），To为箱梁外表面温度；Ta为空气干球温度，K。式（2）可改写为

其中

当平均温度在某一范围内变化时，温度因素θ数值变化不大，因此可近似将表面的辐射换热系数hra看作常数，可取为1.1。

对于对流换热，由牛顿冷却定律可知，箱梁外表面向周围空气进行的对流换热量qca为

式中：hca为箱梁外表面的对流换热系数，W/（m2·K），其计算方法可参考文献[1-2]。

因此，混凝土箱梁外表面对外的总换热量qa为：

式中：ha为表面总换热系数，其计算式为

1.2 综合大气温度的的计算

混凝土箱梁外表面与外界的实际辐射换热量，应为外表面对天空的辐射换热量与对地面辐射换热量之和[2]，即

根据基尔霍夫定律，代入相关系数并简化可得混凝土箱梁外表面与外界的实际辐射换热量q'ra[2]

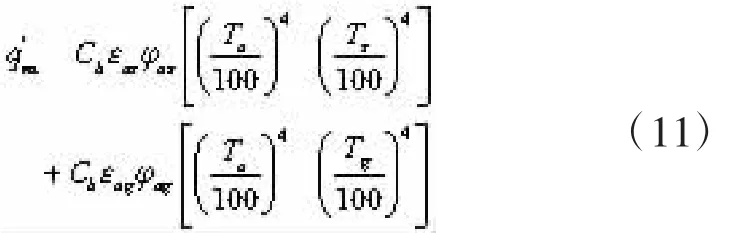
上式可改写为

式中：Ts为天空当量温度；Tg为地面温度；φos、φog分别为箱梁外表面对天空和对地面的辐射角系数；qe为有效辐射，其计算式为

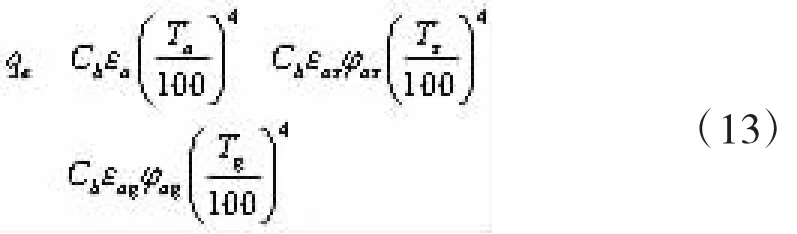
根据热平衡方程式（2），可以得到由箱梁外表面向箱梁内部混凝土的传热量q0，即

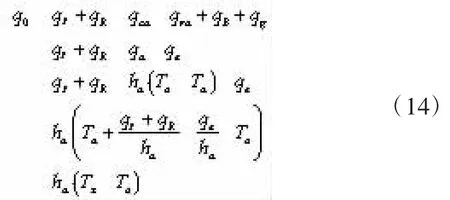
式中：Tz为综合大气温度，它表达了箱梁外空气温度、太阳辐射、地面反射辐射和长波辐射、大气长波辐射对箱梁外表面的综合热作用，其计算式为

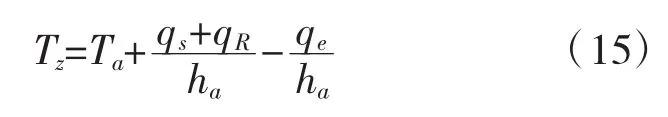
2 箱梁温度场求解

对于箱梁温度场求解中的热传导方程、边界条件及其有限元推导，在众多文献[1，2]中已有涉及，在此不再赘述。本文运用通用有限元程序ANSYS对箱梁温度场进行瞬态分析，现就计算时模型建立及其他问题简述如下。

2.1 单元的选取

本文选用四边形单元来对箱形截面进行网格划分。四边形单元采用PLANE77，单元形状如图1所示，该单元具有8个节点，每个节点上只有一个自由度即温度。

图1 PLANE77单元几何形状图

2.2 材料属性及输入计算数据的确定

在进行混凝土箱梁温度场的分析时，存在选取混凝土热力学参数的问题，而影响这些参数的因素众多，诸如混凝土配合料品种和用量、钢筋和预应力筋的比率，混凝土的龄期和水化热等。本文参考《民用建筑热工设计规程》（GB 50176—1993），取混凝土的比热为920 J/（kg·K），导热系数为1.74 W/（m2·K），混凝土的容重取2 400 kg/m3。

此外参考相关文献[1-2,4-6]，取混凝土表面辐射热吸收系数为0.65，取地面平均反射率为0.2，取箱梁外表面与天空辐射面及地面间的辐射系统黑度为0.9，取大气的黑度为0.8。

2.3 箱形截面网格划分

某预应力混凝土箱梁桥主桥全长586.0 m，上部结构为六跨变高度预应力混凝土连续箱梁结构，其总体布置及控制截面断面如图2所示。

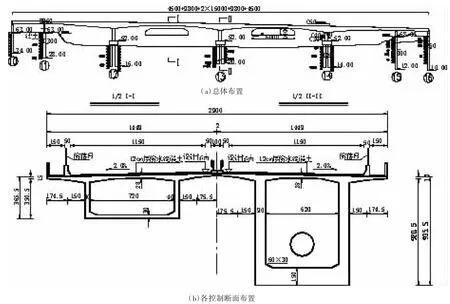
图2 某大跨预应力混凝土箱梁桥（单位：cm）

按箱梁截面实际尺寸建立模型，然后对其进行网格划分，由于顶板处是温度变化最剧烈的部位，因此该处网格划分较密，如图3所示。分析模型由2 500个单元、8 000个节点组成。

图3 箱梁截面单元划分

2.4 加载

由于是进行瞬态分析，所以必须给出初始温度条件。通过实测证明，在夜间混凝土体内的温度与外界气温较为接近，因此本文假定该时刻混凝土内的温度场是均匀的，并采用IC命令来设置混凝土箱梁的初始温度以定义其初始条件。本文在箱梁温度场的分析中，将各种形式的热流按照前面所述的方法转换成对流换热，即将综合对流换热系数和综合大气温度施加在箱梁的边界上。

假定大气降温历程曲线如图4所示（图中时间起点为0：00），即从第38 h开始降温，在10 h内温度降低15℃，随后日温度变化幅度在3～4℃，基于此对上述模型进行加载。

图4 大气温度降温历程

3 计算结果分析

计算结果如图5～图9所示，其中图5和图6为箱梁顶板、底板各点温度变化，图7为箱梁顶板、底板温差变化，图8和图9为最大负温差时刻箱梁顶板、底板温度沿其高度分布。

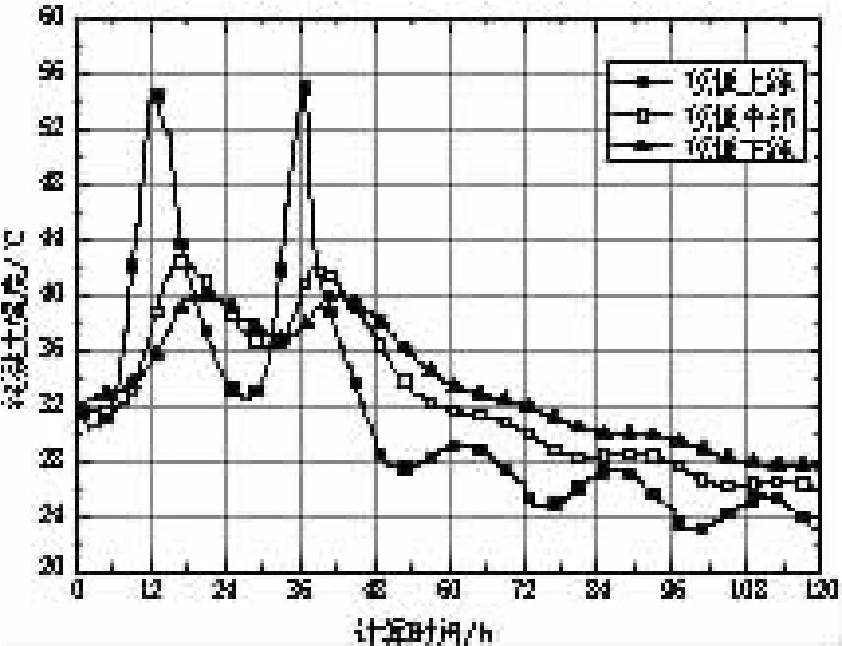
图5 箱梁顶板各点温度变化

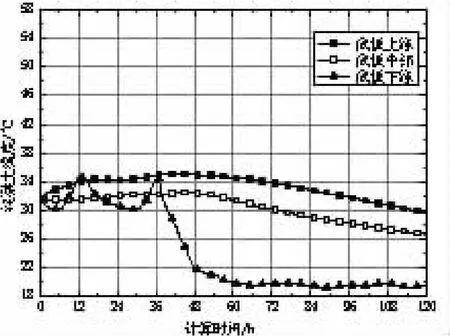
图6 箱梁底板各点温度变化

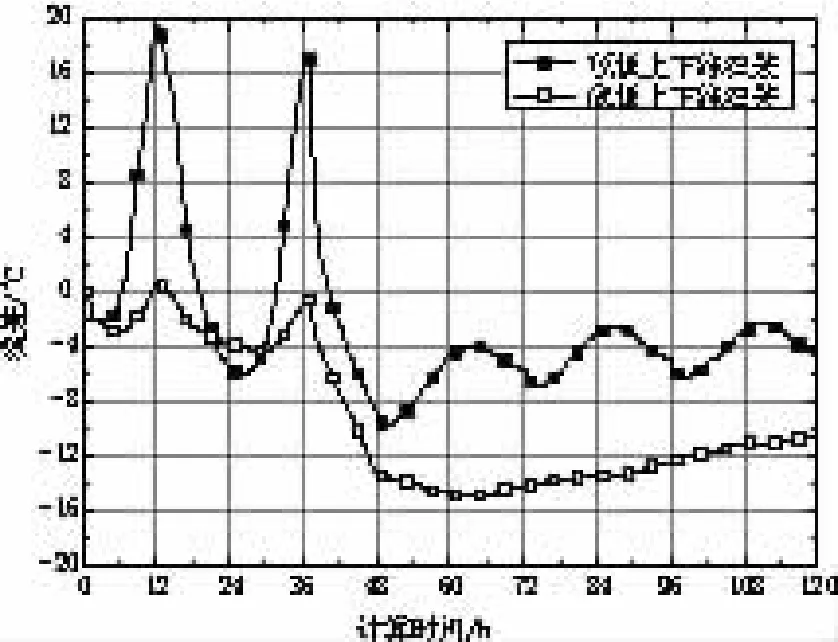
图7 箱梁顶板、底板温差变化

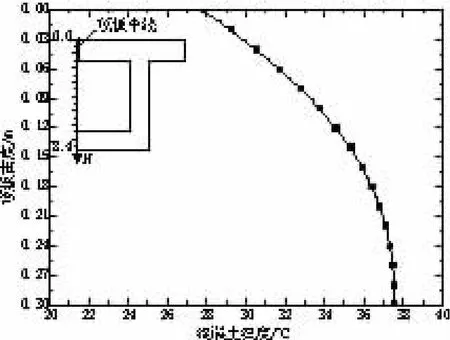
图8 最大负温差时刻箱梁顶板温度沿其高度分布

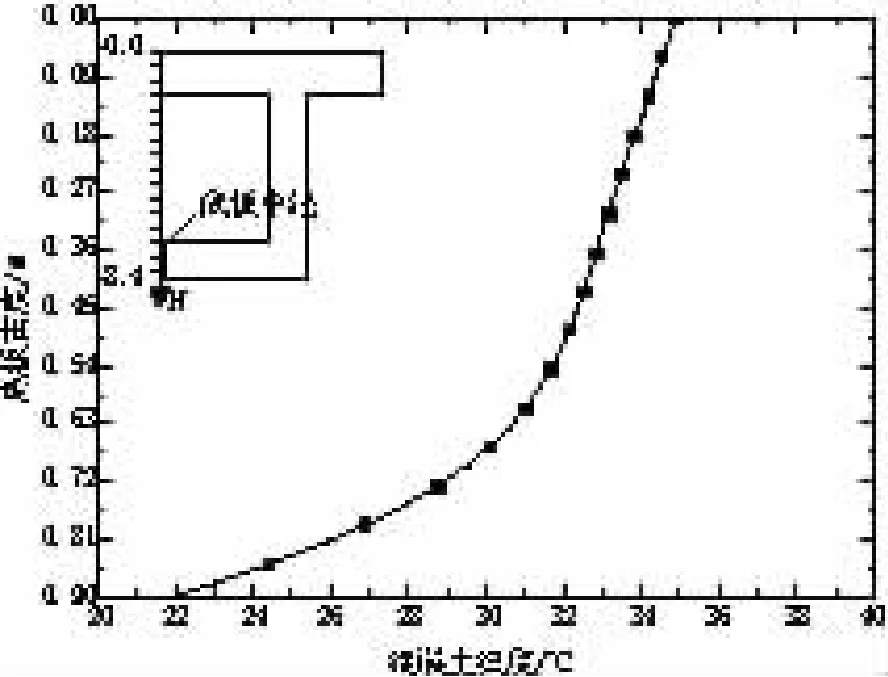
图9 最大负温差时刻箱梁底板温度沿其高度分布

从图5～图9中可以得出以下规律：

（1）箱梁顶板上缘温度变化与大气温度变化规律基本一致，而顶板中部及顶板下缘对大气降温的反应要明显滞后；对于箱梁底板有着同样的变化规律。

（2）箱梁顶板最大负温差出现在第50 h，达9.7℃，随后由于顶板中部和下缘温度持续下降，其负温差有所减小；箱梁底板最大负温差出现在第63 h，达14.7℃，随后其负温差同样有所减小；箱梁顶板和底板在最大负温差出现时刻及其大小上的差别主要是两者壁厚不同所致，前者壁厚仅0.3 m，而后者为0.91 m。

（3）在最大负温差时刻，箱梁顶板、底板温度沿其高度分布可采用双折线模拟。

相对于混凝土正温差模式，国内外学者对负温差梯度模式的研究相对较少，因此仅有少数几个国家的桥梁规范对其做出了规定，如BS 5400、AASHTO 89、AASHTO 94、AASHTO 98等规范，图10即为部分规范中的负温差模式，需要指出的是各规范均是采用多折线形式的函数来描述箱梁负温差，其区别仅仅是温度设计取值的不同。从中可以看出BS 5400中的负温差模式与本文计算结果较为相符，因此在箱梁负温差效应分析时，建议采用BS 5400规范。

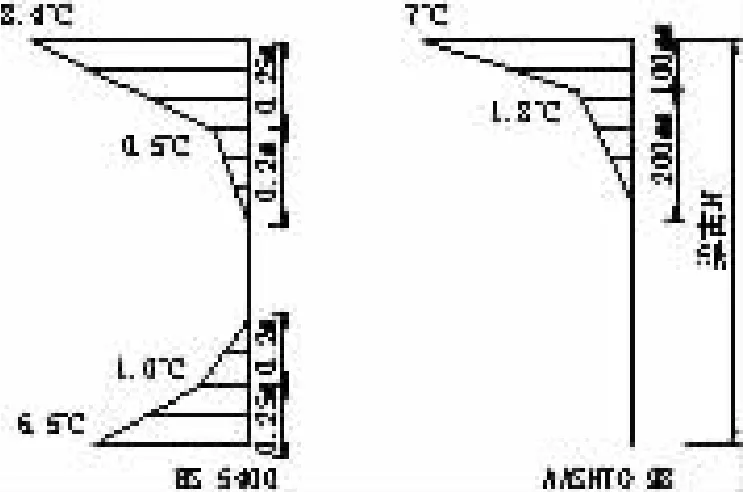
图10 各国桥梁规范负温度梯度模式

4 箱梁负温差效应分析

本文采用BS 5400及AASHTO 98规范中的负温差模式对上述混凝土箱梁桥进行计算，选用实体单元solid65，其模型如图11所示。

图11 ANSYS计算模型（局部）

其结果如图12～图16所示。

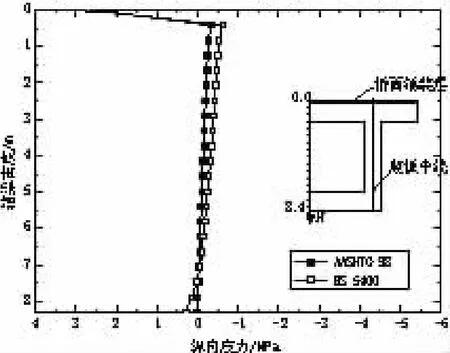
图12 根部截面箱梁腹板中心处纵向应力

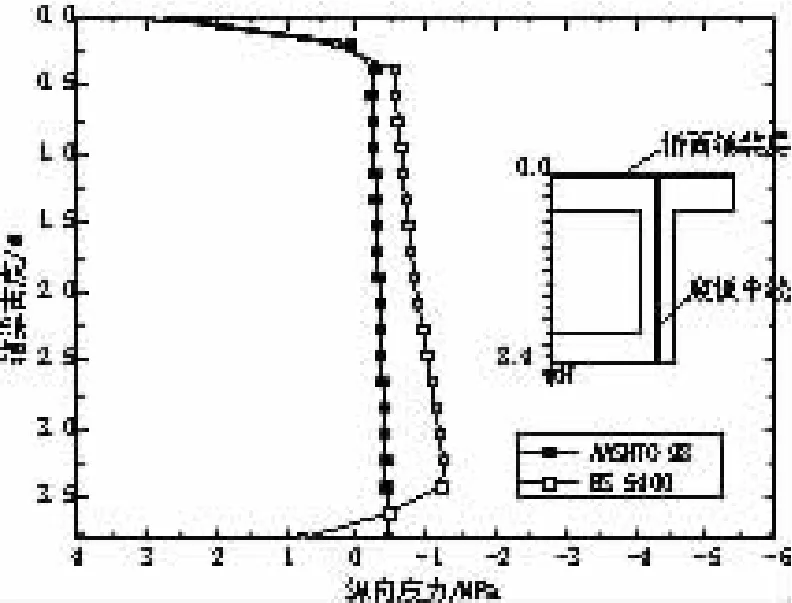
图13 跨中截面箱梁腹板中心处纵向应力

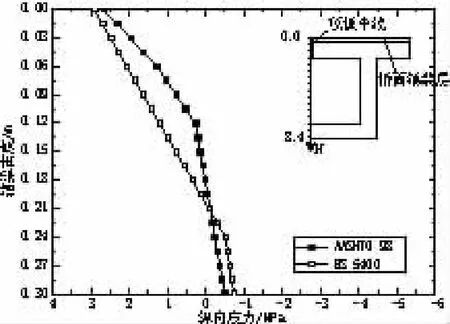
图14 根部截面箱梁顶板中心处纵向应力

图15 跨中截面箱顶板中心处纵向应力

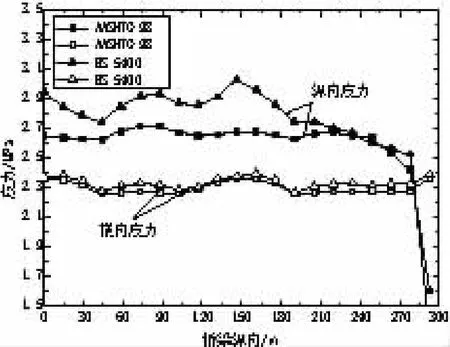
图16 箱梁顶板下缘中点处应力变化

从图12～图16中可以看出：

（1）不论是纵向应力还是横向应力，采用AASHTO 98规范与BS 5400规范负温差模式所计算出的温度应力区别均较小。

（2）就计算结果而言，箱梁顶板上缘纵向应力达到2.9 MPa，其横向应力在全桥范围内都小于纵向拉应力，但仍可达2.4 MPa。

（3）上述计算结果所采用的温度设计值仅为7～8℃，因此如果实际的负温差高于8℃，其顶板上缘的纵向、横向应力则会超过3MPa，可见负温差引起的温度效应较之正温差更应引起重视。

5 结论

本文对混凝土箱梁在降温作用下的温度场进行了详细的分析，从分析结果中可以看出：对于骤然降温温差效应，建议选用BS 5400负温差模式，其温度设计值建议取为10～14℃。

此外，本文对箱梁在负温差作用下的效应进行了计算，发现即使温度设计值仅为7～8℃时，其顶板上缘的纵向、横向应力都在2.4 MPa以上，因此应予以重视。

[1]刘兴法.混凝土结构的温度应力分析[M].北京：人民交通出版社,1991：12-108.

[2]凯尔别克.太阳辐射对桥梁结构的影响[M].北京：中国铁道出版社,1981：4-32.

[3]汪剑.大跨预应力混凝土箱梁桥非荷载效应及预应力损失研究[D].长沙：湖南大学土木工程学院，2007.

[4]Elbadry M M，Ghail A.Temperature variations in concrete bridges[J]. Journalofthe StructuralEngineering,ASCE,1983,109(10)：2355-2374

[5]IzakC.Potgieter,WilliamLGamble.Nonlineartemperaturedistributions in bridges at different loc a tions in the United States[J].PCI Journal,1989,34(4)：81-103.

[6]Dilger W H,Beauchamp J C,Cheung M S，et al.Field measurements of Muskwa River bridge[J].Journal of the Structural Division, Proceedings of the ASCE，1981,107(11)：2147-2161.

[7]叶见曙,贾琳,钱培舒.混凝土箱梁温度分布观测与研究[J].东南大学学报,2002,32(5)：788-793.

U441

A

1009-7716（2016）05-0209-05

10.16799/j.cnki.csdqyfh.2016.05.059

2016-01-27

汪剑（1979-），男，湖北罗田人，博士研究生，高级工程师，从事桥梁工程设计与科研工作。