关于“原子轨道”的概念转变研究

叶思宇　丁　伟

（华东师范大学化学与分子工程学院　上海　200241；华东师范大学化学与分子工程学院　上海　200241)



关于“原子轨道”的概念转变研究

叶思宇丁伟

（华东师范大学化学与分子工程学院上海200241；华东师范大学化学与分子工程学院上海200241)

摘要：“原子轨道”在原子结构中具有特殊地位，并且影响后续学习。通过文献分析，得出有关形成“原子轨道”误概念的普遍原因：受旧量子学说“玻尔理论”干扰和对原子轨道本质“概率”问题不清楚。其概念转变策略，主要分为三方面：借助实验仪器、手工活动和小组合作学习。

关键词：原子轨道；误概念；概念转变

从道尔顿的原子学说到卢瑟福的核型原子模型，人们一步一步地认识原子的内部微观结构。当原有理论不能解释氢原子线状光谱等实验事实时，出现了量子力学。

玻尔引入了部分量子理念，但只能解释氢原子及一些单电子离子的光谱，原因在于其没有完全抛弃经典力学的内容。1926年薛定谔意识到，微观粒子的波粒二象性和不确定性之间的关系，提出了薛定谔方程。通过求解薛定谔方程得出原子的能量和波函数，波函数又被称为“原子轨道”，能量称为原子轨道能。这正是原子轨道的基础，表示核外电子的运动状态，与经典的轨道意义不同，是一种轨道函数。［1］由于高中阶段学生并未接触波函数和薛定谔方程，本文将“原子轨道”理解为电子在核外空间概率密度较大的区域。可由于玻尔行星模型非常形象简单，学生常常深刻记忆，阻碍学生理解原子轨道的本质——概率。本文就此研究学生产生有关“原子轨道”误概念的原因，针对误概念进行概念转变。

一、误概念产生原因分析

1.受旧量子学说“玻尔理论”干扰

不同水平学生都更喜欢具体、简单的抽象模型。例如：原子和分子的全填充模型；玻尔原子模型；八隅体规则等。即使学生在一个很高的教育水平也可能使用简单的抽象模型，例如原子模型的量子化学或分子轨道。［2］文献整理发现，学生对玻尔模型尤为记忆深刻。

物理学家玻尔（Niels Bohr，1885-1962），建立氢原子核外电子运动模型，解释了氢原子光谱，后人称为“玻尔理论”，主要内容：（1）行星模型；（2）定态假设；（3）量子化条件；（4）跃迁规则。［3］后来的新量子论完全抛弃了玻尔行星模型的“外壳”，而玻尔理论的合理“内核”保留下来的。学生们却恰恰相反，牢固地记住了“外壳”，忽略了“内核”。

（1）“轨道”（orbital）的错误认识

学生混用“轨道”（orbital）和“玻尔轨道”（orbit）。“轨道”（orbital）是用来描述在一定能层和能级上又有一定取向的电子云，即电子在核外空间概率密度较大的区域。

Georgios Papaphotis和Georgios Tsaparlis（2008）［4］通过测验题检测学生对基础量子化学的理解程度。其中有一道题为“根据你的猜想，画出氢原子实际的样子。”超过三分之二的学生坚持“行星模型”（即使已经学习量子力学概率模型）。图1为学生的图画表征。

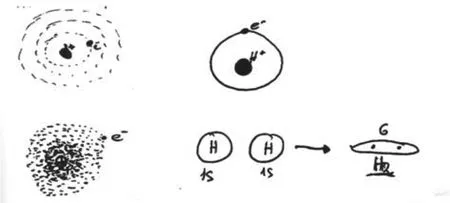
图1　学生图画表征

学生对“玻尔行星模型”记忆深刻，有三个原因：第一，玻尔采用“类比”的方法，将核外电子运行方式比喻成行星围绕太阳运行，非常形象，不用死记硬背；第二，量子化学用电子云表征“轨道”（orbital），学生头脑中并没有类似的“图式”可以“同化”，造成认知记忆障碍；第三，两个理论都用“轨道”表述，使学生产生理解偏差。是否可以将现今的“轨道”（orbital）改称“云层”，以区别于“玻尔轨道”（orbit），一方面体现电子云的表征方式突出本质，另一方面体现了原子轨道（s，p，d.....）能级层次。

（2）“基态”和“激发态”的错误理解

学生受玻尔理论中的行星轨道影响，认为“基态”和“激发态”仍在固定的轨道上，忽略了核外电子在核外运行的本质为“概率”问题。

Georgios Papaphotis和Georgios Tsaparlis（2008）测试题“在基态氢原子的1s轨道的空间外有可能发现电子吗？说明原因。”。这道题目大约20％的人回答正确。大部分认为，在“1s区域”外发现电子，只有可能是被激发了。这些错误答案都是基于对轨道的“确定性”认识，认为电子是在一个固定空间中运动。

2.对原子轨道本质“概率”问题不清楚

学生无法对原子轨道本质“概率”问题理解清楚的原因在于，无法理解“为什么微观粒子不能像宏观物体一样用确定的‘轨迹’来描述物体的运动规律？”。其中“海森堡不确定原理”起关键作用。只要明白“不确定原理”为什么“不确定”，就能明白为什么要用“概率”描述微观粒子运动规律。

（1）海森堡不确定理论

海森堡（W，Heisenberg，1901-1976）论证到，对于一个物体的动量（mv）的测量的偏差（△mv）和相对该物体的运动坐标，也就是该物体的位置（x）的测量偏差（△x）的乘积处于普朗克常数的数量级，即：

Δx·ΔP≥h（4∏）

这个关系式被称为海森堡不确定关系式。用此公式考察氢原子的基态电子，发现电子在相当于玻尔半径的约5倍（260/53）的内外空间里都可以找到（包括在原子核上），这样，玻尔半径以及线性轨道变成了无稽之谈。因此采用“概率”描述微粒粒子的运动规律。

学生不理解“海森堡理论的本质是由电子本身特性引起而非测量工具问题”和“为什么是物体动量和物体位置之间的偏差”。其实不确定性关系适用于所有物质的普遍原理，不确定性是物质的内在本质。对于宏观物体，看似物体的位置和速度是可以准确确定的，但这只是因为宏观物体的不确定性相对微小，不易察觉而已。事实上，不确定关系揭示的是一条重要的物理规律：粒子在客观上不能同时具有确定的坐标位置及相应的动量。［5］“不确定关系式”其实是根据量子力学基本方程推导出来，而非凭空想象。

而为什么是位置和动量之间的关系呢？描述一个物体的运动规律，需要知道物体的位置和速度，但是速度又与质量有密切相关性即动量，不确定关系就是反应微观粒子运动的基本规律，所以体现在位置和动量两个物理量上。

（2）电子云

电子云是电子在原子核外空间概率密度分布的形象描述，图像中每一个小黑点表示电子出现在核外空间中的一次概率（不表示一个电子），概率密度越大，小黑点越密。

Georgios Papaphotis and Georgios Tsaparlis（2008）测试题“观察图中1s和一个2p轨道电子云图［图2 （a）和（b）］。在（a）中远离原子核处有稀疏的点，而（b）中这样点则没有。你认为是其中一张错了还是两张图都错了？”

图2　1s（a)和2p（b)

许多学生认为两张图的不同是由于轨道本质的不同（一个s-，另一个是p-）：

“s轨道的形状是圆形的，然而在p轨道有两个‘耳垂’”，“两个图片都是正确的，因为（a）指的是s轨道（圆形）而（b）是p轨道（两个‘耳垂’）——事实上在p轨道中，靠近原子核处电子密度更大，而远离原子核时密度就减小了”……

无论什么轨道，远离核的部分都有可能出现电子，只是出现的概率小、稀疏，并不取决于属于哪一个轨道。而且学生很容易受“电子云轮廓图”所误导，认为电子就是出现在这个范围之内，而忽略了轮廓图只表示了95％的电子出现的区域。

二、概念转变策略

1.借助实验仪器

由于“原子轨道”的抽象性和不可视性，研究者研发了一些实验仪器将轨道可视化。

Charles Leonard Hurwitz［6］采用原子探测器（atomic explorer）学习原子的电子结构的本质。Shane P.Tully［7］等人用Jmol软件将类氢轨道网络点彩可视化（web-based pointillist visualization of hydrogrnic orbitals）。类氢轨道的电子密度点彩图是根据蒙特卡洛方法（Monte Carlo method）进行交互作用。蒙特卡洛方法又称“统计模拟法”，以概率和统计理论为基础的一种计算机方法。将网络应用程序和Jmol观察器相结合，可获得清晰准确的三维轨道形状和大小，最多可呈现到轨道主量子数5（如图3）。

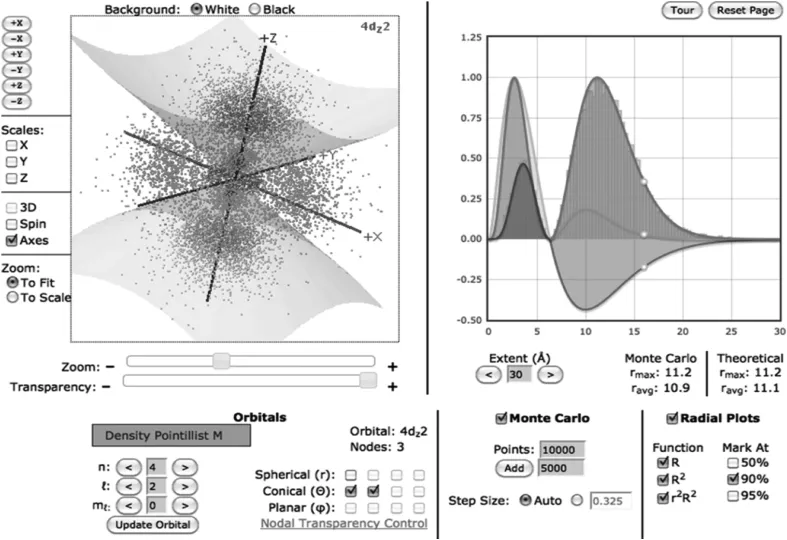
图3　带有圆锥型节点的4d（z2)轨道的蒙卡特罗程序点彩图屏幕截图和二维径向平面图展示90％径向密度

2.手工活动

Zephen Specht和Duke Raley［8］设计了一项活动帮助高中生理解不同电子轨道类型（特别是s，p，d和f轨道）。学习轨道和相关的电子密度，发现电子围绕原子核的概率问题。

用一个小弹球扔在白纸上（放在一系列复写纸上面），用来表示电子密度（如图4）。根据s，p或d轨道的不同类型，将白纸折成不同的形状，用这个方法可以使得白纸上的一些地方不与复写纸相结合，来表示节点。“原子核”就是白纸的中心位置。首先学生要学会如何将白纸折成不同的轨道类型，在白纸两面都印有虚线方便学生折叠。纸1：s轨道不用折叠；纸2：p轨道沿着三条虚线折叠，使得白纸中间形成一个“山脊”；纸3：d轨道沿着两个垂直的三条虚线折叠，适当的折起白纸，两个交叉的“山脊”，减去中间的部分，形成一个“X”的图案。用纸夹将纸2和3中间的“山脊”夹住。然后模拟电子云，向纸的中心位置原子核扔弹球。由于白纸下有复写纸，当球落在白纸上时留下印记。弹球扔25次就能在纸1上形成很好的点分布（s轨道），纸2用50次（p轨道）和纸3用75次（d轨道）。

图4　一个学生将弹球扔在纸上

整个过程，学生体会到“为什么轨道有特别的形状”，而且能够将轨道表示的字母（s，p，d和f）与它们的光谱发射谱线特征：锋利（sharp）、主要的（principal）、散开的（diffuse）、基础的（fundamental），建立联系。学生最后还要完成一个工作单，将二维图像转换为三维图像，加强了对电子轨道构型的理解。

3.小组合作学习

Georgios Tsaparlis和Georgios Papaphptis（2009）［9］采用小组形式在教师的观察指导下完成特定学习任务。小组有3-4个成员，其中至少有一个学生持有正确观点。例如，当学生讨论“氢原子的原子轨道表征方式”的时候，有一组学生原本的观点如图5（学生A画的是d图，学生B画的是b图，然而学生C画的更接近a图（并说明外面的一圈是“s轨道”））。

图5　学生氢原子图画表征

他们的对话如下（教师为T）：

T：B，虚线指的是什么？

B：是1s，...这个空间里有许多轨道，1s，2s，2p，所有的这些组成了层。

T：这个就是你画的轨道吗？

B：是的，轨道和层。

T：C，你是如何理解的呢？

C：我试着解释轨道不是一个能精确描述的空间，...但是在中心位置确实是原子核，但是最大的圈表示一部分在这里面，这个更大的圈里s轨道被包括，就是发现电子的可能范围。

T：A，你是怎么认为的呢？

A：我已经把氢原子的原子中心放上一个质子，这些点随着远离原子核变得更加稀少，实际上我已经画出了可能性，就是可能发现电子的位置。

T：我们已经看到了所有的图画，哪些能体现问题中所提到的真实性？

B：A能够体现，因为有原子核存在，也能体现在1s中发现电子的可能性，甚至从原子核到无穷远的地方也不会是0。

T：C你是如何认为的？

C：同意。

T：那我们对照看自己所画的图？

C：降低了可能性，在一定距离后就变成0了。

从对话中发现，教师能够针对学生

理解的“关键处”进行指导。观察多组讨论发现，大部分学生可以接受电子云是电子在瞬间出现的不同可能点的位置，但不能接受用这样的一张图表征氢原子内部“看到”的样子。所以学生不能够用静态图表示，结果又回到了行星模型。此时教师用一个类比的方法帮助学生理解，用一个自行车快速旋转，辐条所呈现的样子帮助学生理解电子云图可以表示氢原子的动态时的样子。这样的讨论可以激发学生最真实的想法，从本质上进行概念转变。

三、小结

总结以上三种概念转变策略，小组合作学习能够从本质上解决对“玻尔理论”的根深蒂固理解，在对话中引发认知冲突并建立正确概念，但这种方法所需时间较多。实验仪器能够将微观结构表现得淋漓尽致，给予视觉冲击的同时理解原子的微观结构。但考虑各学校的条件不同，这种方法的局限性也暴露无遗。手工活动能够让学生亲身体验轨道的形成过程，且所需材料方便易得，体会不同轨道的形状的同时，理解“不确定性理论”。每种方法各有优缺点，只要教师恰当使用，概念转变就不是问题。

参考文献

［1］宋天佑.简明无机化学［M］.北京：高等教育出版社，2007

［2］Christina Stefani，Georgios Tsaparlis.Students's Levels of Explanations，Models，and Misconceptions in Basic Quantum Chemistry：A Phenomenographic Study［J］.Journal of research in science teaching，2009

［3］北京师范大学，华中师范大学，南京师范大学无机化学教研室编.无机化学上册（第四版)［M］.北京：高等教育出版社，2002：27

［4］Georgios Papaphotis and Georgios Tsaparlis，Conceptual versus algorithmic learning in high school chemistry：the case of basic quantum chemical concepts Part 2.Students' common errors，misconceptions and difficulties in understanding ［J］.Chem.Educ.Res.Pract.，2008，9：332–340

［5］杨福家著.原子物理学［M］.北京：高等教育出版社，2008

［6］Charles Leonard Hurwitz.Evaluating conceptual change in high school honors chemistry studentsston［J］.United States：Boston University School of Education，2006

［7］Shane P.Tully，et al.Interactive Web-Based Pointillist Visualization of Hydrogenic Orbitals Using Jmol［J］.J.Chem.Educ.2013，90：129-131

［8］Zephen Specht，Duke Raley.Modeling electron Density and Atomic orbitals using marbles and carbon paper：an exercise for high school students［J］.J.Chem.Educ.2014，91：151-153

［9］Georgios Tsaparlis，Georgios Papaphptis.High-school students' conceptual difficulties and attempts at conceptual Change：The case of basic quantum［J］.International Journal Science Education，2009，31，7：895-930

doi：10.3969/j.issn.1008-0546.2016.04.004

文章编号：1008-0546（2016）04-0010-03

中图分类号：G632.41

文献标识码：B