基于混合威布尔分布拖拉机使用可靠性分析

王艳芳，敖长林（1.东北农业大学工程学院，哈尔滨　150030；2.黑龙江科技大学管理学院，哈尔滨　150028）



基于混合威布尔分布拖拉机使用可靠性分析

王艳芳1,2，敖长林1*
（1.东北农业大学工程学院，哈尔滨150030；2.黑龙江科技大学管理学院，哈尔滨150028）

摘要：选用两参数混合威布尔模型，评估拖拉机系统可靠性。在故障信息获取不够完备情况下，建立故障模式与故障应力之间关联关系，避免故障机制分析；将故障模式按故障应力相似性模糊聚类，实现故障数据分类,基于最小二乘法得到混合威布尔分布参数估计。结合拖拉机故障数据，采用混合威布尔模型拟合故障过程，分析拖拉机可靠性；对比混合威布尔模型与单一威布尔模型可靠度曲线，得出使用混合威布尔模型评估拖拉机可靠性合理性。为提高拖拉机可靠性、维修性提供参考依据，为分析机械系统故障相关性奠定理论基础。

关键词：混合威布尔模型；可靠性；模糊聚类；故障应力；故障机制

王艳芳,敖长林.基于混合威布尔分布拖拉机使用可靠性分析[J].东北农业大学学报,2016,47(3):94-101.

Wang Yanfang,Ao Changlin.Analysis of tractor operational reliability based on mixed weibull distribution[J].Journal of Northeast Agricultural University,2016,47(3):94-101.(in Chinese with English abstract)

为适应作业发展季节性强、时间集中且条件强度高的现状[1]，农业机械产品功能不断完善，结构日益优化。但我国农业机械普遍存在使用寿命短、故障多发、可靠性较差等问题。与发达国家规定拖拉机平均无故障工作时间300 h相比，国产拖拉机规定为210 h，部分农机实际平均无故障工作时间仅达20～30 h[2-3]。

评估机械可靠性水平时，常用寿命分布有正态分布、指数分布、对数分布和威布尔分布[4]。威布尔分布是最常用形式[5-8]。采用单一威布尔模型进行系统可靠性评估，一般忽略系统故障机制差异性。对于复杂可修系统，如拖拉机故障数据多为非独立同分布形式，单一威布尔模型无法适用。混合威布尔评估模型是把故障数据按不同故障机制分类，弥补单一威布尔模型缺陷[11-12]。Wang等应用三参数混合威布尔模型进行多种故障模式、多种原因数控机床可靠性分析[13]；张根保等应用混合威布尔分布进行加工中心可靠性评估[14]；朱海平等进行卧式加工中心现场失效数据结合威布尔混合模型分析实例研究[15]。前人研究多集中在数控机床可靠性评估，利用完备故障信息针对具体故障模式或故障过程建立混合威布尔模型[16-17]。在农业机械领域，农机多为复杂机械系统，工作环境复杂，故障机制多样，混合威布尔评估模型故障数据多来源于维修人员记录，故障信息不完备，直接故障数据分类难以实现。

本文应用混合威布尔模型拟合复杂机械系统故障过程，在难以获取完备故障信息情况下，建立故障模式与故障应力关系，避免故障机制分析。对故障模式按故障应力相似性进行模糊聚类，混合威布尔模型分析；结合拖拉机田间作业跟踪试验故障数据，采用混合威布尔模型评价拖拉机可靠性，与单一威布尔模型对比。为分析机械系统故障相关性奠定理论基础。

1　混合威布尔评估模型

1.1混合威布尔模型

威布尔模型失效分布函数，

该模型适用条件为[5]，建立模型对象为故障发生时间和系统要求故障机制相同至少相似。

混合威布尔分布考虑系统多种机制并存，其模型包含更多参数，因此能针对较为复杂情况进行数据拟合。如果一个总体由m个子体组成，对应各子体均服从相同分布，但参数不同，设各子体概率密度函数分别为：

各子体混合权数分别为：

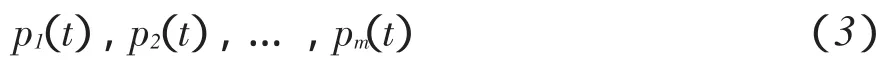
则总体概率密度函数为：

若每个子体都服从威布尔分布，即fi（t）表达式为：

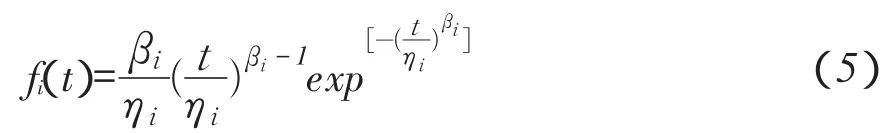
式中，βi-第i个威布尔分布形状参数，ηi-第i个威布尔分布尺度参数，pi-第i个威布尔分布权重，表示第i种失效原因或失效模式失效数据在产品总失效数据中所占比例，满足下式条件：

根据概率密度函数与累积失效概率函数微分关系，总体累积失效概率函数为：

式中，Fi（t）第i个子体累积失效概率函数。

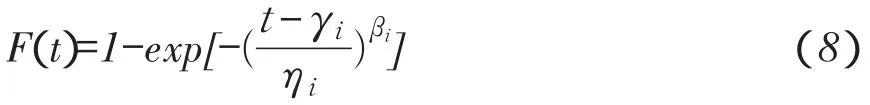
则第i个子体可靠度为

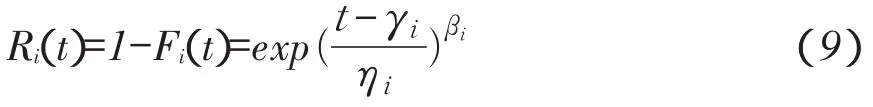
故混合威布尔模型总体可靠度为：

总体失效率函数为：

混合威布尔模型研究总体，如果分为m个子体，则称该模型为m重；一般模型中包含β、η、γ三个参数，研究机械可靠性时，一般令γ=0，即常用2个参数[8-10]。根据收集数据特点及具体系统故障机制特征，采用相应形式混合威布尔模型，如两参数二重模型、三参数二重模型等。

1.2混合威布尔模型参数估计

使用混合威布尔模型进行参数估计，首先需将数据分类，对于每一子体，使用单一威布尔模型拟合其故障过程。对单一威布尔模型线性化，由威布尔失效分布函数式得：

对式（12）两边分别取两次对数得：

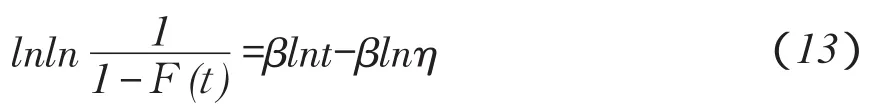
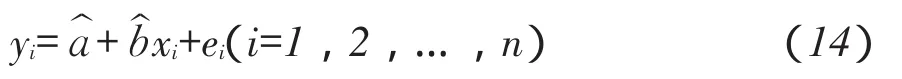
由原始观测数据，利用回归分析最小二乘法计算式（14）参数a和b估计值：

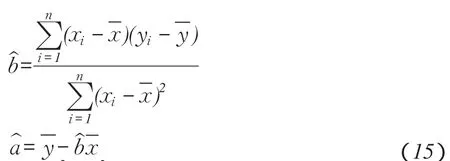
根据a和b估计值，可以计算

2　故障数据预处理

机械系统故障模式一般用发生故障时现象描述，故障现象可能是具体部件，如液压泵漏油；可是某一子系统，如发电机损坏；也可是某一具体零件，如离合器片磨损、水泵轴承损坏等。

2.1故障模式特征属性

通常故障用故障应力、故障机制和故障模式三要素表征。由于机械系统复杂性，三要素间存在多种组合关系，如图1所示[15-17]。

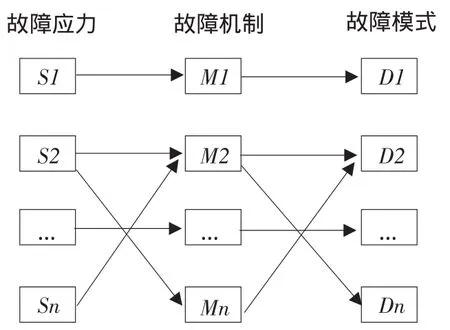
图1　故障应力、机制与模式关系Fig.1 The relationship of failure stress,mechanism and pattern

复杂机械系统故障数据主要来源于维修人员，维修记录主要包括故障发生时间、故障部位、故障现象及维修方式简单描述，由于故障记录信息不完备，在农业机械使用现场收集的故障数据很难直接分析归类。同一故障现象，在试验观测时间范围内，早期失效期、偶然故障期和疲劳期，同一故障现象发生故障机制可能不同，故障机制分析无法完成。故障应力是对故障机制影响最大因素，相同故障应力作用过程相似，不同应力作用过程则不同；故障应力在寿命不同阶段对系统各零部件作用则相对稳定。为避免故障机制分析，以故障应力相似性表征故障机制相似性，建立故障模式与故障应力关系，将故障模式分类，满足混合威布尔模型要求。

2.2故障数据模糊聚类分析

本文以具体故障现象作为故障模式特征属性，以故障应力相似性表征故障机制相似性，通过模糊聚类方法，对故障数据聚类分析。模糊聚类对象为机械系统故障模式集合F={F1，F2，…，Fn}，其中每个对象Fi=（i=1，…，n）包括m类故障现象，即Fi={fi1，fi2，…，fim}，fij表示故障模式Fi第j个故障现象。应力集合记为S={s1，s2，…，sk}，表示系统受到k种应力作用。模糊聚类步骤如下：

步骤1：利用专家打分法，得到系统故障现象f受故障应力S影响权数。

每个故障现象fij受k种应力S={s1，s2，…，sk}作用权数由专家打分获得，即：

fij=（w1j，w2j，…，wkj），其中

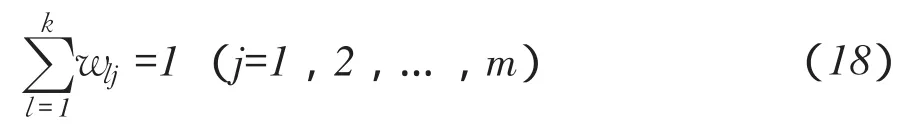
式中，wlj（l=1，…，k）表示故障现象fij受故障应力S={s1，s2，…，sk}作用权数。

步骤2：建立故障模式与故障应力之间关系。

由于Fi={fi1，fi2，…，fim}，则以故障现象为特征属性故障模式Fi（i=1，…，n）为：

Fi=（Wi1，Wi2，…，Wik），其中

式（19）中Wij表示故障模式Fi受故障应力S= {s1，s2，…，sk}作用权数，其值等于故障模式Fi包含故障现象所受应力作用权数之和。

则以k个故障应力S={s1，s2，…，sk}表征n个

故障模式F={F1，F2，…，Fn}特征属性矩阵为：

步骤3：建立故障模式模糊相似矩阵。

根据式（20）特征属性矩阵B，建立模糊相似矩阵A=（aij）n×n，其中aij表示Fi与Fj相似度[18]，

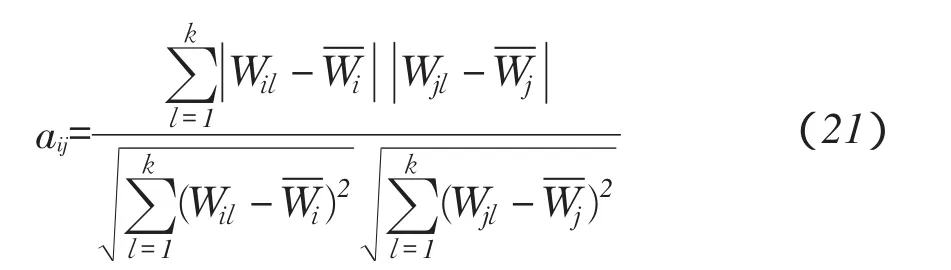
步骤4：求模糊矩阵A模糊等价矩阵A。

通过式（21）求得矩阵A，具有自反性和对称性，但一般不满足传递性，因此进一步求A传递→闭包t（A）。从矩阵出发A，计算A→A2→A3→…→Al，直至第一次发现Al＝A2l，则Al就是A传递闭包t（A）[19-21]。具体计算公式如下：

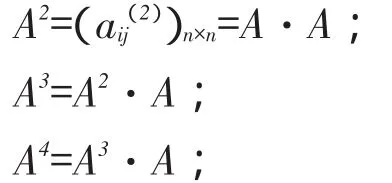
此时Aλ矩阵中元素只有0和1，将元素相同列对应故障模式归为一类，从而完成故障数据分类，满足混合威布尔模型可靠性评估要求。

3　实例分析

对黑龙江省北安市某农场7台某型号履带式拖拉机进行故障跟踪试验。试验期间共发生各类故障184次。维修人员现场记录拖拉机故障数据主要包括故障发生时间、故障部位、故障现象及维修方式。由于记录信息主要为故障简单描述，不够完备，故障数据无法直接归类分析[22]。利用混合威布尔模型进行拖拉机可靠性评估，首先需要对故障数据预处理。

拖拉机各故障模式在维修记录中表征为具体故障现象[23]，试验期间故障模式可表示为以下11种常见模式：

F={F1，F2，…，Fn}={轴承受损、功能失效、电路受损、磨损、烧蚀、渗漏、堵塞、橡胶类部件受损、变形、松脱、意外损坏}，每种故障模式表现故障现象如表1。

表1　故障模式Table 1 Failure pattern

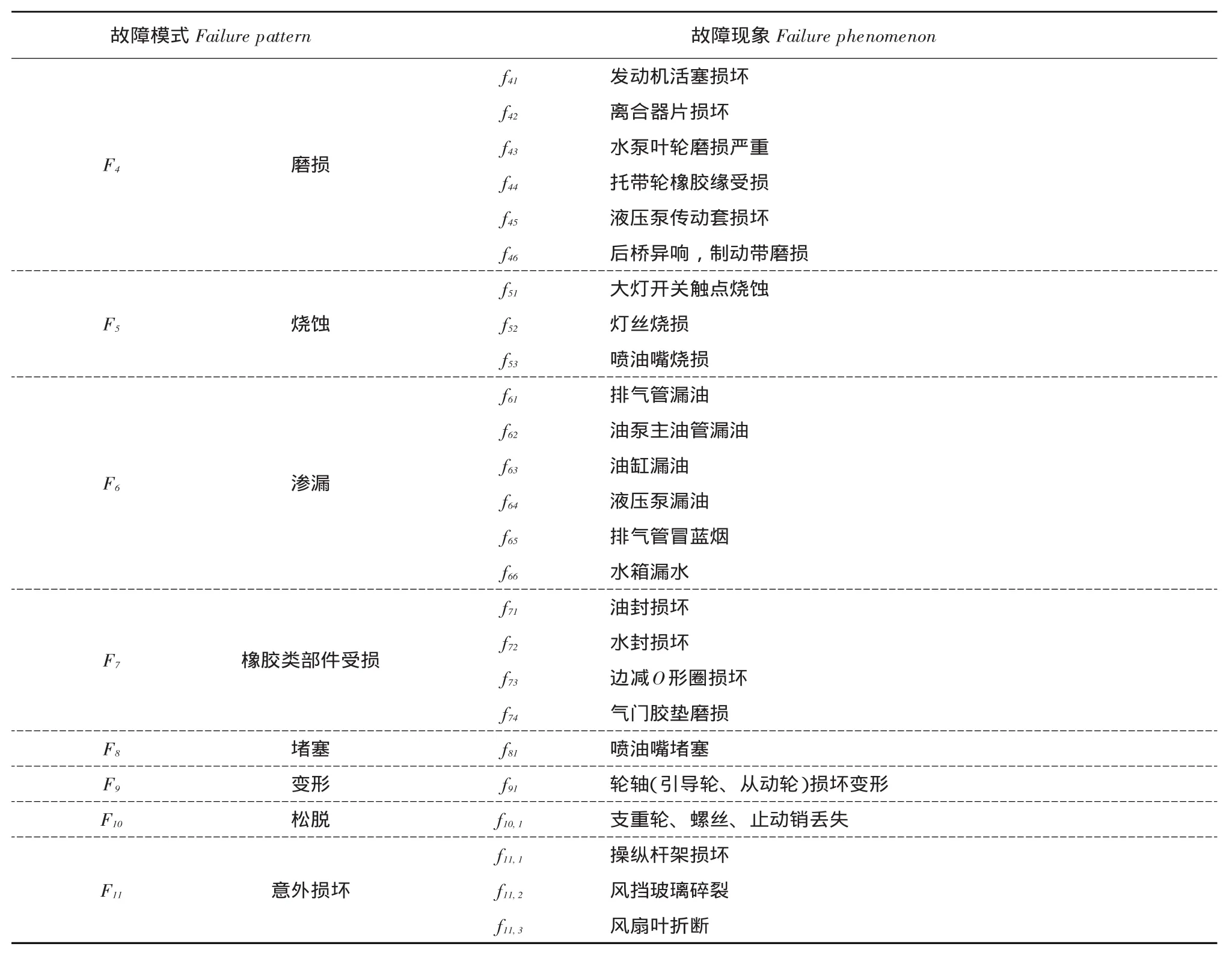
续表

以故障模式“F1=轴承受损”为例，其故障现象为F1={f11，f12，f13，f14，f15，f16}={变速箱轴承损坏，后桥轴承损坏，水泵轴承损坏，拖带轮、引导轮轴承损坏，液压泵、发电机、起动机轴承损坏，边减轴承损坏}。

拖拉机作业过程中，主要受到故障应力为：

S={s1，s2，s3，s4，s5，s6}={温度应力、冲击应力、振动应力、气压液压应力、摩擦应力、化学腐蚀应力}。

采用专家打分法，得故障模式F1={f11，f12，f13，f14，f15，f16}受应力S={s1，s2，s3，s4，s5，s6}影响矩阵为：

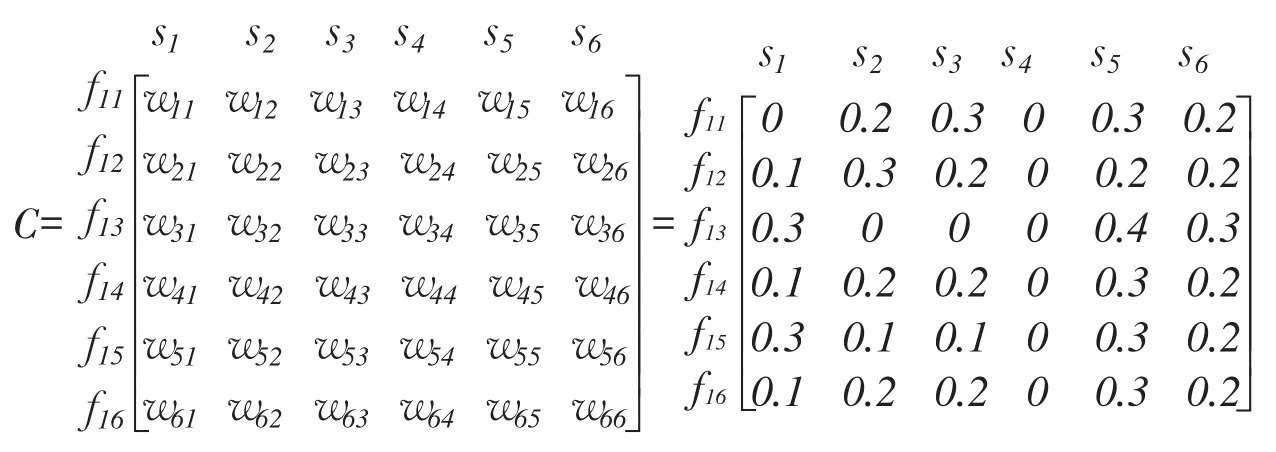
则故障模式F1={f11，f12，f13，f14，f15，f16}，则F1受各故障应力影响权值向量为：

F1=（W11，W12，…，W16）=（0.9，1，1，0，1.8，1.3），

其中W1j=（j=1，…，6）

同理可得其他故障模式F2，…，F11受故障应力影响权值，则

根据故障模式特征属性矩阵，建立模糊相似矩阵A=（aij）n×n，其中

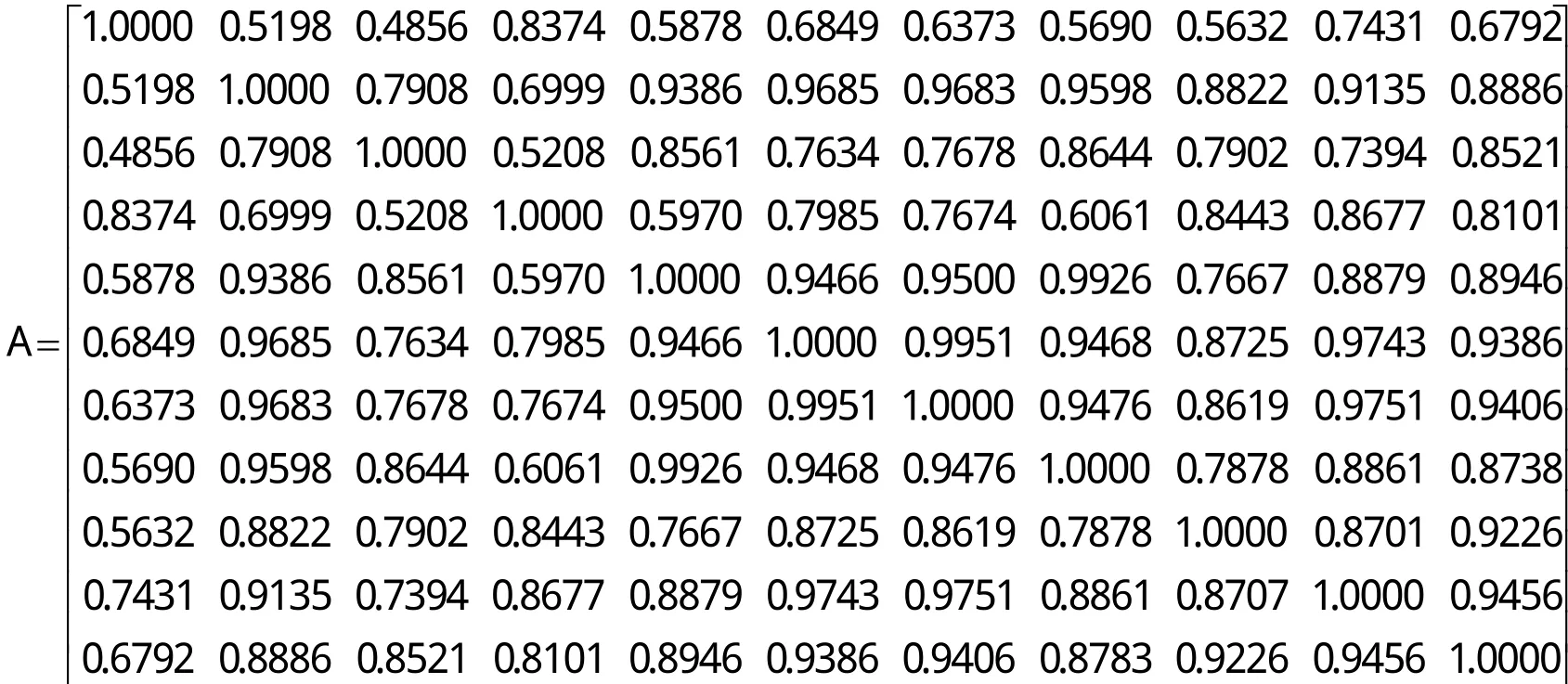
根据模糊聚类步骤4，可得A闭包矩阵-A：

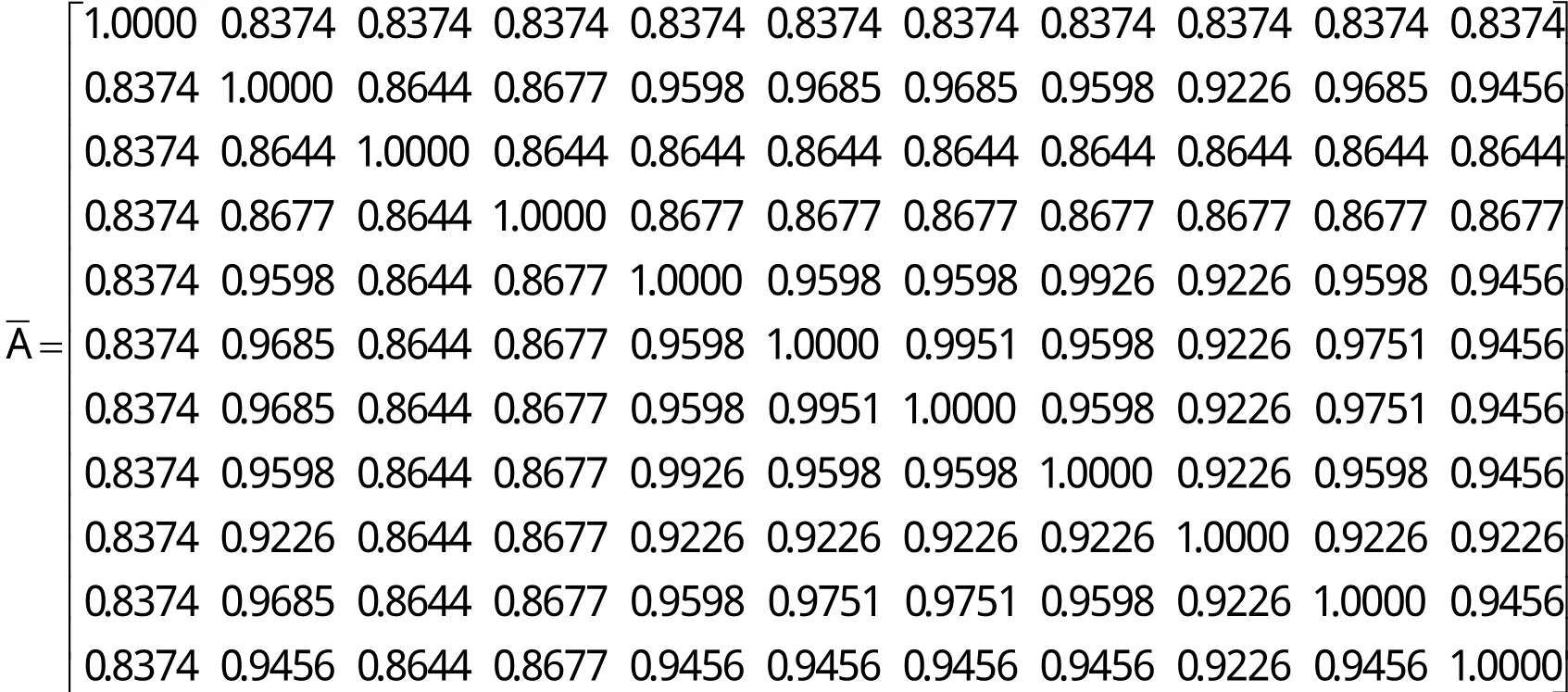
根据模糊聚类方法，聚类阈值λ取值为：

1，0.9951，0.9926，0.9751，0.9685，0.9598，0.9456，0.9226，0.8677，0.8644，0.8374

阈值越大，分类数越多。

取λ=0.8677，根据式（22），计算得等价关系矩阵为：

由此故障模式可分为{F1}，{F3}，{F2，F4，F5，F6，F7，F8，F9，F10，F11}三组。

每组故障数据故障发生时间如表2～4所示：

表2　拖拉机轴承受损故障发生时间（单位：作业小时）Table 2 Failure data of tractor bearings(Unit:operating hours)

表3　拖拉机电路受损故障发生时间（单位：作业小时）Table 3 Failure data of tractor circuit(Unit:operating hours)

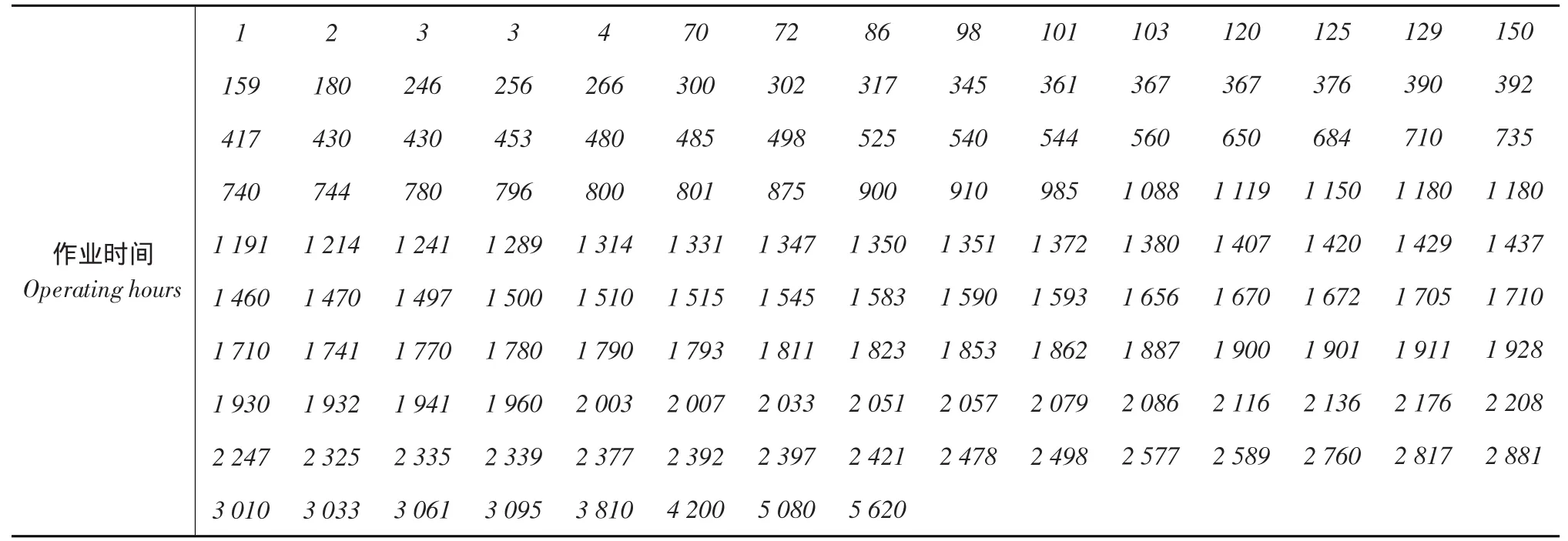
表4　拖拉机其他故障发生时间（单位：作业小时）Table 4 Rest failure data of tractor(Unit:operating hours)

由此，实现了故障数据分类。

根据表2～4数据，以威布尔模型拟合故障过程，可得：

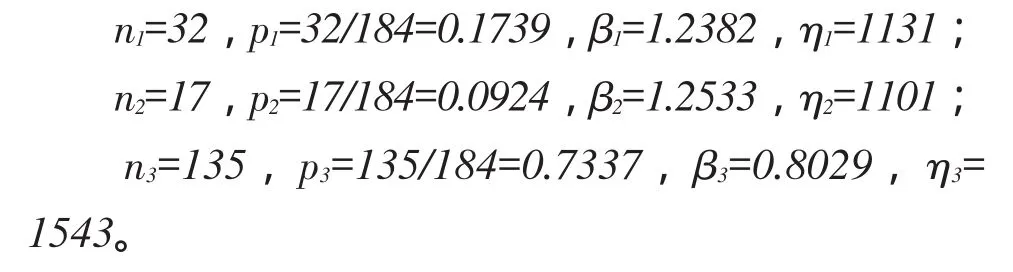
则混合威布尔模型系统可靠度为：

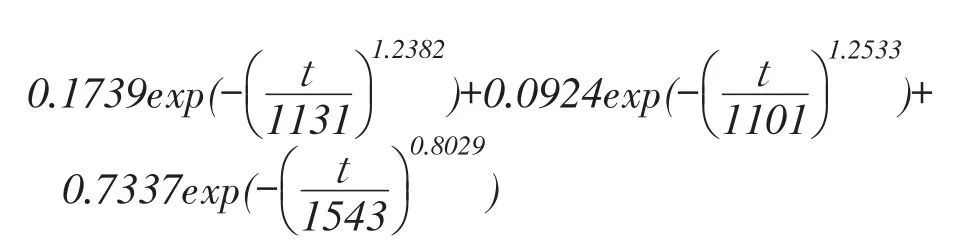
单一威布尔模型计算各参数值分别为：

β=0.9012，η=1411。

则单一威布尔模型系统可靠度为：

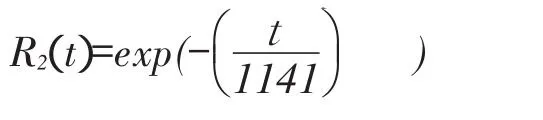
混合威布尔模型与单一威布尔模型可靠度曲线对比图如图2所示。

由图2可知，混合威布尔模型可靠度函数为实线，单一威布尔模型可靠度函数为虚线。通过对比，混合威布尔模型评估拖拉机可靠度明显低于单一威布尔模型计算结果。混合威布尔模型考虑了系统复杂性和故障机制多样性，同时在产品使用调查中，发现用户可靠性感受明显低于单一模型评估结果。因此可以认为，混合威布尔评估结果更合理。

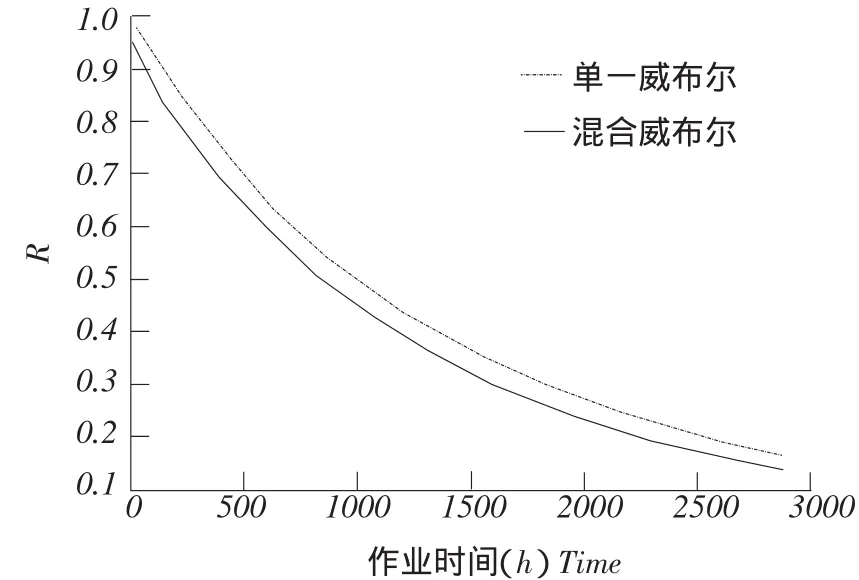
图2　混合与单一威布尔模型系统可靠度对比Fig.2 Comprising the reliability curve of mixed weibull model with the single weibull model

4　结　论

a.在故障记录信息不完备前提下，以故障应力相似性表征故障机制相似性，解决混合威布尔模型要求数据按故障机制分类难题；

b.建模对象立足于故障发生时间，避免难度大、工作量大故障机制探测及分析工作，可为研究故障特性、故障相关性和可靠性评估提供参考。

[参考文献]

[1]敖长林,李一军,闫相斌,等.基于非齐次泊松过程拖拉机发动机使用可靠性[J].机械工程学报,2007,43(10):206-210.

[2]苏佳,敖长林,焦扬.基于模糊神经网络拖拉机使用可靠性评价[J].东北农业大学学报,2008,39(12):99-103.

[3] Krivtsov V V.Practical extensions to NHPP application in repairable system reliability analysis[J].Reliability Engineering and System Safety,2007,92(5):560-562.

[4]敖长林,郑先哲,谢里阳,等.基于神经网络拖拉机可靠性模型参数估计[J].农业机械学报,2004,35(3):31-33.

[5]敖长林,乔金友,戴有忠.威布尔过程场合下现场可靠性试验统计分析[J].东北农业大学学报,2000,31(3):303-306.

[6]凌丹,黄洪钟,张晓铃,等.混合威布尔分布参数估计L-M算法[J].电子科技大学学报,2008,37(4):634-640.

[7]王继利,杨兆军,李国发,等.基于改进EM算法多重威布尔可靠性建模[J].吉林大学学报,2014,44(4):1010-1015.

[8]高翔,王若平,夏长高,等.随机变量多重Weibull统计模型及参数最优估计[J].农业机械学报,2006,37(11):41-44.

[9]Lai C D,Murthy D N P,Xie M.Weibull distributions and their applications[J].Springer Handbook of Engineering Statistics,2006(3):63-78.

[10]Murthy DNP,Bulmer M,Eccleston J A.Weibull model selection for reliability modelling[J].Reliability Engineering & System Safety,2004,86(3):257-267.

[11]Townson P,Murthy DNP.A Critical evaluation of Weibull accelerated failure models[J].Quality Technology & Quantitative Management,2007,4(1):35-50.

[12]Bucar T,Nagode M,Faidiga M.Reliability approximation using finite Weibull mixture distributions[J].Reliability Engineering and System safety,2004,84(3):241-251.

[13]Wang Z,Yang J,Wang G,et al.Application of three-parameter Weibull mixture model for reliability assessment of NC machine tools:a case study[J].Proceedings of the Institution of Mechanical Engineers,Part C:Journal of Mechanical Engineering Science,2011,225(11):2718-2726.

[14]张根保,杨兴勇,李磊,等.基于混合威布尔分布加工中心可靠性评估[J].计算机应用研究,2015,32(11):3278-3282.

[15]朱海平,邓超,刘繁茂,等.卧式加工中心现场失效数据分析实例研究[J].计算机集成制造系统,2010,16(10):2293-2297.

[16]Pascual F.Accelerated life test planning with independent Weibull competing risks with known shape parameter[J].IEEE Transactions on Reliability,2007,56:85-93.

[17]张根保,郭书恒.基于竞争威布尔模型加工中心可靠性评估[J].计算机集成制造系统,2015,21(1):180-186.

[18]Chen C C,Chen M S.Hicluse:highly scalable Density- Based Clustering with heterogeneous cloud[J].Procedia Computer Science 2015,53(1):149-157.

[19]Bonzo D C,Hermosilla A Y.Clustering panel data via perturbed adaptive simulater annealing and genetic algorithms[J].Advances in Complex Systems,2002,5(4):339-360.

[20]扶名福,谢明祥,饶泓.模糊聚类分析法在抽风机故障诊断中应用[J].工程力学,2007,24(1):36-40.

[21]朱桂英,夏吉庆,施灿璨,等.基于模糊聚类方法沼气工程综合评价指标体系构建[J].东北农业大学学报,2015,46(6):104-108.

[22]赵继俊,邹经湘.可靠性实验数据混合威布尔分布参数优化估计[J].农业机械学报,2000,31(5):106-109.

[23]郝志勇,张凤嘉,刘伟.自动调角冷却风机内流动机理数值模拟研究[J].东北农业大学学报,2013,44(5):115-119.

Analysis of tractor operational reliability based on mixed weibull distribution

WANG Yanfang1,2,AO Changlin1(1.School of Engineering,Northeast Agricultural University,Harbin 150030,China; 2.School of Management,Heilongjiang University of Science and Technology,Harbin 150028,China)

Abstract:Two- parameter mixture Weibull distribution model was established on the basis of failure data gathered from the tractors operating in field conditions.As it was difficult to obtain the complete failure information,the relationship between the failure- pattern and failure stress was established to avoid the failure mechanism analysis.The failure data was classified by Fuzzy clustering based on the similarity of failure stress,and the parameters of the mixed weibull model was estimated based on the Least Squares Method.Combining the failure data of the tractor by tracing test,the reliability of mechanical system was analyzed by using the mixed weibull model.By comprising the reliability curve of mixed weibull model with the single weibull model,it was more reasonable in the mixed model for the evaluation of tractor reliability.The result of research could be used as references for the improvement of reliability and maintainability of tractor ,and as theoretical basis for study on the interrelation between mechanical system failures as well.

Key words:mixed weibull model; reliability; fuzzy clustering; failure stress; failure mechanism

*通讯作者：敖长林，教授，博士生导师，研究方向为农业系统工程、系统可靠性、评价理论与方法。E-mail:aochanglin@gmail.com

作者简介：王艳芳（1979-），女，讲师，博士研究生，研究方向为农业系统工程，可靠性建模与仿真。E-mail:w329648086@sina.com

基金项目：国家自然科学基金项目（71171044）

收稿日期：2015-12-06

中图分类号：TH128

文献标志码：A

文章编号：1005-9369（2016）03-0094-08