基于卷积窗的动目标检测雷达滤波器组的设计
贾哲

摘 要:分析了动目标检测雷达多普勒滤波器组的不足,提出了一种新的基于加卷积窗的FFT滤波器组,改善了雷达处理增益。理论推导和检测性能仿真结果表明,在频率偏移时,基于加卷积窗的FFT滤波器组具有比传统FFT和WFFT更好的检则性能。
关键词:动目标检测;雷达;滤波器组;FFT
中图分类号:TN957.51 文献标识码:A DOI:10.15913/j.cnki.kjycx.2016.08.010
动目标检测(MTD)雷达是利用多普勒效应检测目标信息的脉冲雷达,其核心为多普勒滤波器组,常用快速傅里叶变换(FFT)实现。但是,FFT的高旁瓣效应在强杂波环境中会造成大量的虚警,甚至可能淹没真实的目标。因而,必须采用时域加权方式,通过减少频谱泄漏降低滤波器的旁瓣。
针对回波频率偏离滤波器中心频率的FFT失配情况,文献[1]通过交替运用加窗傅里叶变换(WFFT)和离散小波变换(DWT)这两种方法,在整个频率范围内得到了非最佳的折衷处理效果,而且提升了系统的复杂程度。文献[2]在文献[1]的基础上提出了基于单边形式海明窗的FFT/WFFT-DWT方法,进一步提高了检测性能。本文探讨了一种新的卷积窗FFT方法(CWFFT)。该方法能够减少频谱泄漏,增加雷达的信息处理增益,提高检测性能。
1 MTD雷达滤波器组的工作原理
在MTD雷达的信号处理中,在杂波抑制器后串接的窄带滤波器起着重要的作用,它是相干脉冲串的匹配滤波器,对输入脉冲进行相干积累。采用数字信号处理技术时,可以通过横向滤波器或FFT实现。
MTD雷达信号的具体处理流程为:雷达接收机接收回波后经过高频放大、混频、中频放大等环节,将信号变为中频信号,再经过零中频正交双通道处理,将信号变为视频信号;将视频信号通过主杂波对消器,滤除零频率杂波后进行多普勒滤波;经多普勒滤波处理后,再作恒虚警处理,得到目标的多普勒信号。在实际工作中,多普勒滤波可以由横向滤波器或FFT实现。当滤波器的数目较大时,采用FFT算法可以大大简化操作步骤。
2 卷积窗FFT滤波器的原理
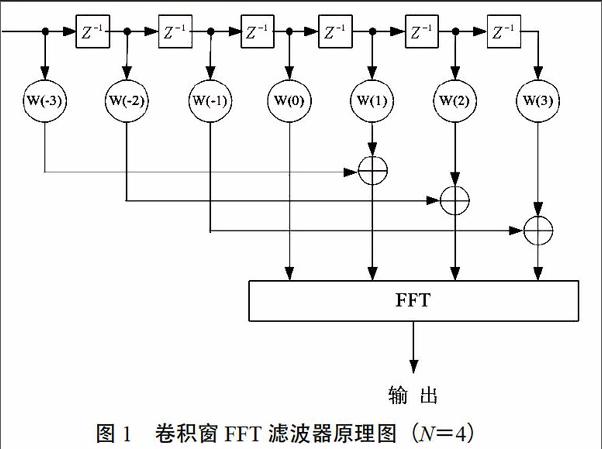
当回波输入频率恰好等于FFT滤波器组的某一中心频率,且输入未被加权时,FFT滤波器等效于匹配滤波器,其改善因子最大。但由于FFT的旁瓣增益较大,杂波和噪声有可能从旁瓣进入滤波器。因此,通常要对相参脉冲进行加窗处理。常用的窗函数有Hamming窗、Hanning窗和Blackman窗等。与矩形窗(不加窗)相比,这些窗函数旁瓣增益较小,但是主瓣展宽了,能降低滤波器的频率分辨率。对此,本文提出了一种加卷积窗FFT滤波器,通过将相参脉冲串经过延时和加权操作后再进行傅里叶变换,这样可以改善滤波器组的频谱特性。图1为当相参脉冲数N=4时的卷积窗FFT滤波器原理。与传统的加窗处理相比,卷积窗FFT具有较大的主瓣增益和较好的旁瓣衰减频率特性。
3 信号处理增益分析
3.1 理论分析
假设滤波器组输入信号由雷达信号和加性高斯分布白噪声组成,则雷达信号表示为:
S(n)=Aexp[j(2πfn+θ)]. (1)
式(1)中:A为正弦的幅度;f为信号的频率;θ为随机初相位;n=0,1,…,N-1,N为原始信号长度。
FFT的输入信号表示为:
x(n)=S(n)+NI(n)+jNQ(n). (2)
式(2)中:NI(n)为噪声的同相分量部分;NQ(n)为噪声的正交分量部分。
当窗函数为Hamming窗时,WFFT的处理增益表示为:
. (3)
. (4)
WFFT-DWT的处理增益表示为:
. (5)
卷积窗FFT(CWFFT)的处理增益为:
. (6)
3.2 实验量化分析
表1以传统FFT精确匹配条件下的信号处理增益为参照,给出了采用CWFFT与WFFT在不同频偏时的相对信号处理增益。WFFT采用的窗函数分别为矩形窗、Hamming窗,CWFFT采用分别基于这两种窗函数的卷积窗。由于窗函数具有一定的对称性,因此正负频偏时的PG是相同的。本文只讨论频偏在[0,0.5]区间内的情况。
由表1可知,WFFT在频偏较大时增益比FFT略好,但在频偏较小时增益不如FFT。这说明,WFFT在抑制旁瓣频谱泄漏的同时降低了主瓣内的信噪比。然而,在不同频偏下,CWFFT的增益都要大于FFT和WFFT的增益。这说明,CWFFT具有良好的频域特性,在不同的频偏下能够取得较好的检测结果。
4 结论
由于动目标的多普勒频率不能与FFT滤波器组精确匹配,雷达常常处于失配状态。鉴于此,本文提出了卷积窗FFT方法,它能够较好地抑制旁瓣频谱泄漏,提高检测性能。
参考文献
[1]马晓岩,袁俊泉.基于WFFT/FFT-DWT并行处理提高MTD检测性能的新方法[J].系统工程与电子技术,2000,22(12):27-28.
[2]简涛,苏峰,何友,等.利用FFT/WFFT-DWT提高雷达处理增益的性能分析[J]系统仿真学报,2007,19(8):1879-1882.
〔编辑:刘晓芳〕

