基于三阶剪切形变理论的复合层合矩形板水下声辐射研究
胡昊灏,高 岩
(中国船舶科学研究中心 a.船舶振动噪声重点实验室;b.江苏省绿色船舶技术重点实验室,江苏 无锡 214082)
基于三阶剪切形变理论的复合层合矩形板水下声辐射研究
胡昊灏a,b,高 岩a,b
(中国船舶科学研究中心 a.船舶振动噪声重点实验室;b.江苏省绿色船舶技术重点实验室,江苏 无锡 214082)
以简化的三阶剪切形变理论为基础,由虚功原理建立了较厚复合层合矩形板水下振动与声辐射方程,通过Rayleigh-Ritz法求解系统方程。为了验证所给方法的正确性将计算结果与有限元法计算结果进行对比,并将三阶剪切形变理论(TSDT)所得声辐射解与一阶剪切形变理论(FSDT)计算结果进行对比,指出前者在计算复合层合板声辐射上的优势。最后通过改变杨氏模量,剪切模量,铺层厚度,纤维铺设角等参数,指出影响复合层合板声辐射的主要因素和分频段变化规律,可为水下典型结构声辐射预报和噪声控制提供参考。
三阶剪切形变;复合层合板;声辐射;噪声控制
0 引 言
复合层合材料具有轻质高强,耐腐蚀等优良特性,因而被广泛地应用于船舶工业中。由于复合材料本身构成的复杂性,其动力学特性要远复杂于各向同性材料[1]。
近年来,对复合层合材料动力学的研究主要分为两类方法,第一类是以三维弹性理论为基础的研究[2],该方法需要建立各层弹性力学方程,结合应力应变的边界条件以及连续性条件联合求解,由于没有对应力分布作任何假设,计算极其繁琐,只有当层数很少,加载方式边界条件都很简单时才能求解。另一类则是以二维弹性理论为基础,包括经典层合板理论(CLPT)[3]、一阶剪切形变理论(FSDT)[4-6]、高阶剪切形变理论(HSDT)[7]和离散层理论[8]等方法,它们是在三维弹性理论的基础上对沿厚度方向的应力分布作适当假设而得到的,吴梵[9]在求解正交加筋复合夹层板的弯曲问题时,对面板和底板采用基于Kirchhoff假设的CLPT理论,而对芯层采用基于mindlin模型的FSDT理论。Daneshjou[10-11]也利用这两种理论求解了无限长复合层合圆柱壳的隔声量问题,Cao[12]用FSDT理论求解了无限加双周期肋骨平板的远场声压。CLPT理论忽略了剪切和转动惯量,仅适合薄板,FSDT是目前应用最多的,但该理论假设沿厚度方向的剪切应变为常数,需要引入剪切修正因子,而事实上剪切修正因子的获取较复杂。考虑到经典层合板理论与一阶剪切形变所存在的问题,本文采用简化的三阶剪切形变理(TSDT)论来分析复合层合矩形板的声辐射问题,该方法将位移场用厚度坐标的三次方展开,更能真实地反映层间应力分布,所含未知数个数与一阶剪切形变理论相同,且不需要引入剪切修正因子。
以往的文献关于有限大弹性薄板声辐射的研究已经很成熟[13],但关于复合层合板(尤其是有限大复合层合板)的声辐射问题,由于其动力学模型的复杂性和应用隐秘性而鲜有涉及,本文利用变分法首先建立复合层合板水下声辐射模型,然后求解并分析材料参数和几何参数对辐射噪声的影响,最后给出了一些有意义的结论,为水下典型结构声辐射预报提供参考。
1 模型描述
如图1所示,取一由纤维加强的复合层合矩形板,将其四条边均简支于无限大刚性障板上,板的上侧为无限大水域,下侧为真空,考虑在机械点力激励下复合板的声辐射问题。
1.1 位移场
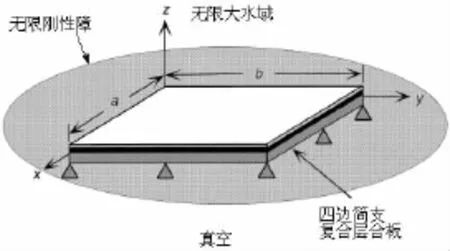
图1 复合层合板声辐射示意图Fig.1 The schematic of sound radiation for laminated composite plate
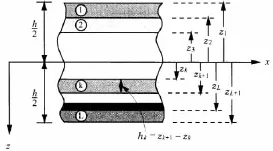
图2 复合层合矩形板各层横向分布Fig2 The transverse distribution for each layer
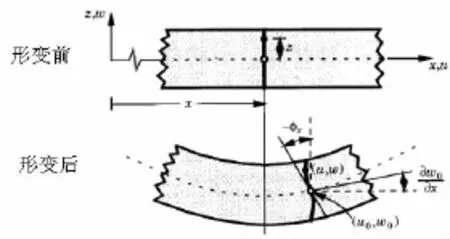
图3 复合层合板位移形变Fig3 The deformation of the plate
结合图2,图3,将位移展开为厚度坐标的三次函数形式,即:

其中:u0、v0和w0为中性面上的位移,φx、φy、θx、θy、λx和λy为待定参数。
θx、θy、λx和λy可以通过层合板上表面和下表面的剪切应力自由的边界条件[7]求得,即:

经过化简后位移场仅含五个未知变量,这与一阶剪切形变理论(FSDT)所包含的未知数是一样的。

其中:系数c1=4/3h2(h为板的总厚度)。
1.2 非线性应变场
与三阶剪切形变位移理论对应的复合层合板的应变场可由Von Karman非线性理论给出:
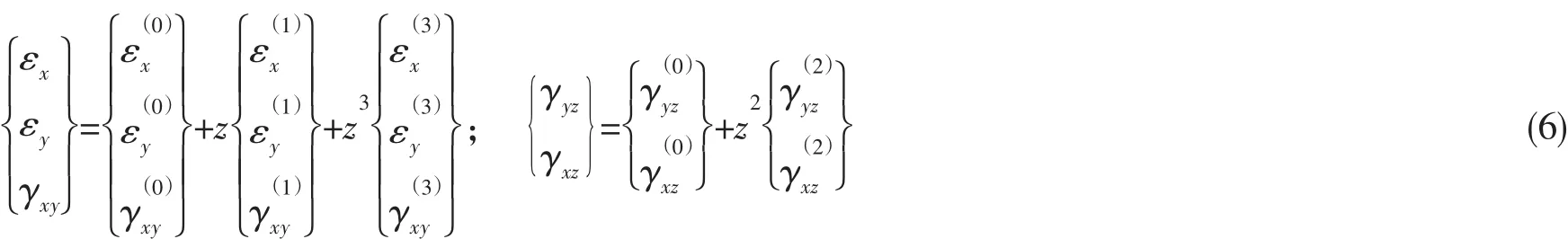
1.3 合成应力及合成力矩

其中:N表示面内合成应力,M表示合成力矩,P、Q和R表示高阶合成应力,A、B、D、E、F和H为不同类型的刚度矩阵。

1.4 流载声压
无限大水域中的声压p满足Helmholtz方程:

其中:k0=ω/c0为声场波数,c0为水中声速。
在复合层合板与流体接触表面满足法向振速连续性:

通过求解方程声场声压的表达式可由Rayleigh积分给出:

其中:ρ0为流体密度,为板表面振速,R为板表面上的点与场点的距离。
2 系统运动方程与方程求解
利用Hamilton原理(即虚功原理)可知:

符号δ表示变分,V,T和Wex分别为系统应变能、动能以及外力做功。将应力、应变以及位移表达式(3)-(8)代入(14)式,然后利用分部积分使虚位移δu0、δv0、δw0、δφx和δφy分离出来且令它们的系数为0,即可得到系统的Euler-Lagrange运动方程:
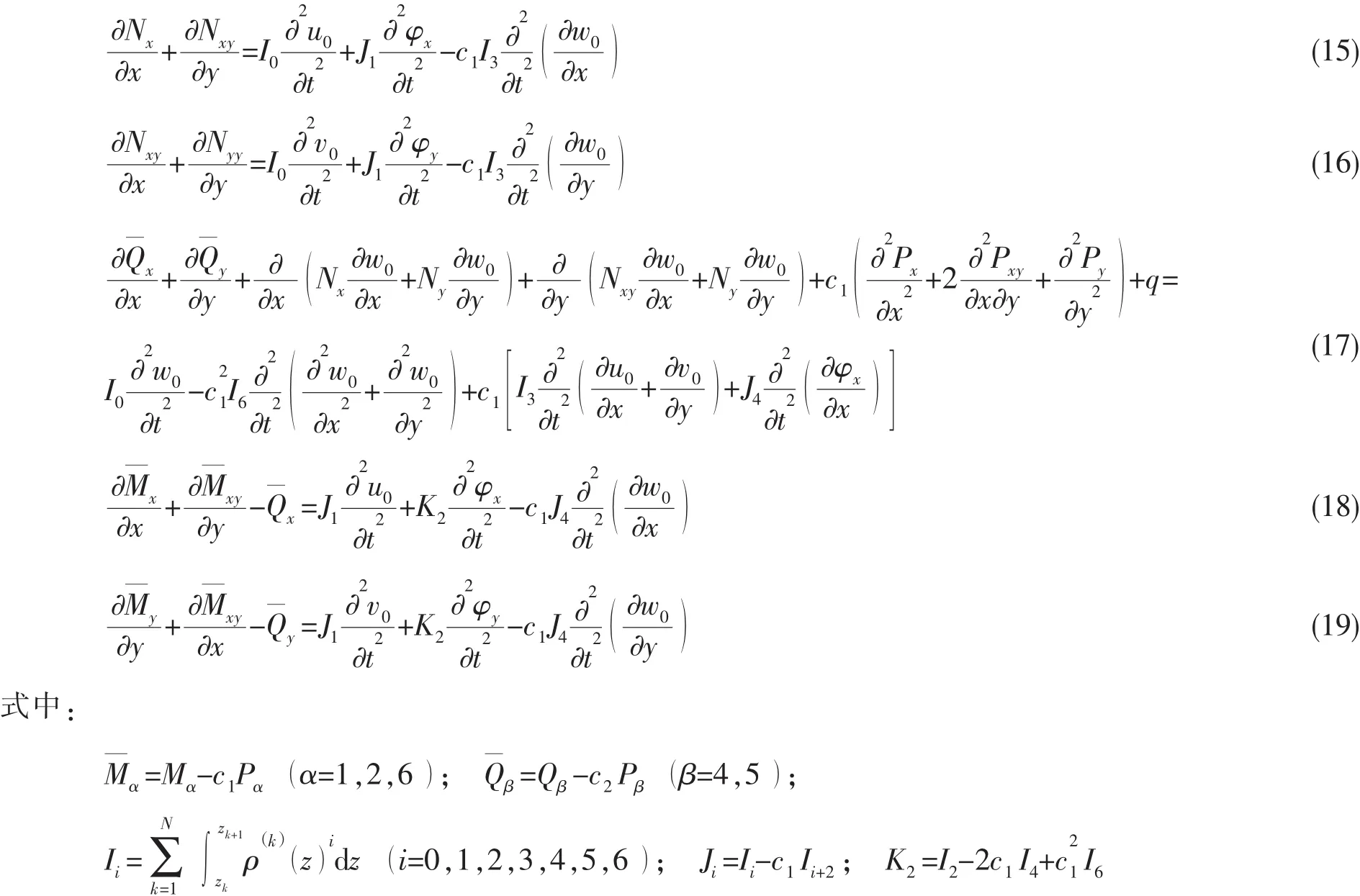
其中:q表示作用在复合层合板上的激励,在这里q=F-p,F表示谐和点激励F=F0δ(x-x0)(y-y0),p表示板表面流体载荷声压,其表达式由Rayleigh积分(13)给出。
2.1 Rayleigh-Ritz解
以反对称角铺设纤维材料的复合层合板为例,当满足四边简支边界条件时形式解可设为:
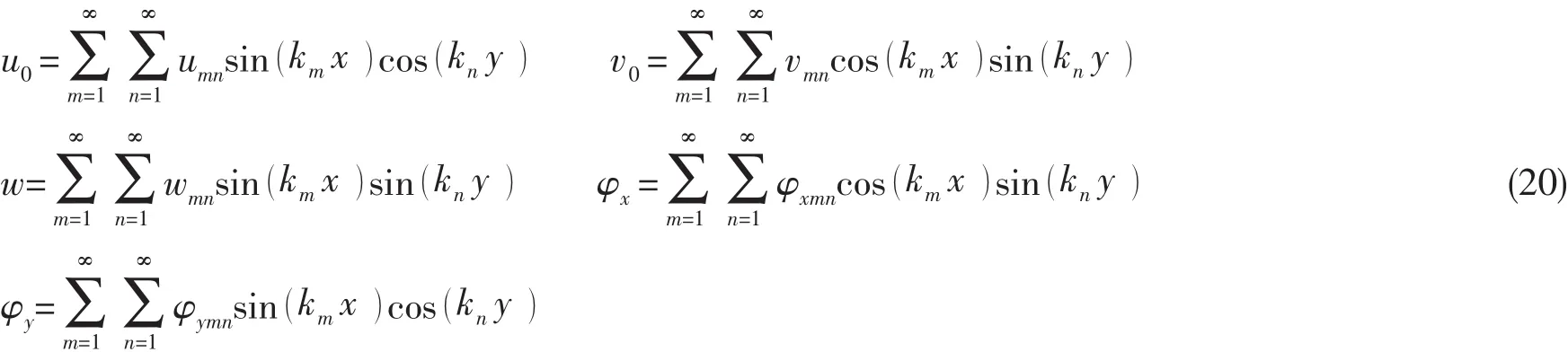
其中:km=mπ/a,kn=nπ/b

式中:Sij、mij分别为刚度矩阵和质量矩阵,pmn为声压模态幅值:

Zmnpq为复合层合板表面辐射声阻抗,其表达式为:
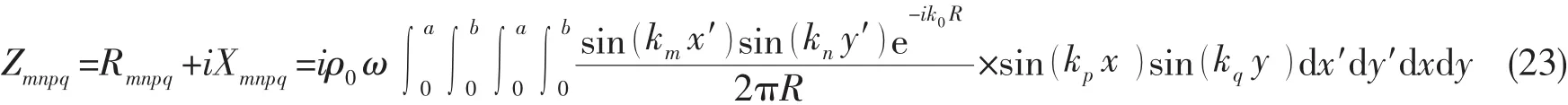
求解系统运动方程(21)可得到夹芯板横向位移模态幅值wmn,进一步可得到系统的均方振速以及辐射声功率表达式。

3 模型验证与参数分析
所分析复合层合板由六层单层板构成,各层厚度相等均为h=0.002(m),板长度a=0.6(m),宽b= 0.6(m),为了计算方便,假设各层材料相等,纤维铺设角度分别为 [45°/-45°/45°/-45°/45°/-45°]。杨氏模量E1=1.2×1011(Pa),E2=1×1010(Pa);泊松比υ12=0.4,υ21=0.4;剪切模量G12=G23=5.9×109(Pa),G13=3× 109(Pa);各层材料密度均为1 600(kg/m3)。激励点位置为(0.3 m,0.2 m),激励力幅值为1(N)。振速参考级为5×10-8(m/s),辐射声功率参考级为0.67×10-18(w)。
3.1 算法验证
以往的文献中关于有限复合层合板声辐射的计算很少,为了验证所建模型的正确性,本文利用有限元商业软件Ansys计算模型的均方振速,取复合层合材料Solid186单元来进行对比验证,Solid186单元为20节点三维实体单元,每个节点有三个自由度,位移按厚度坐标的二次方展开,支持材料的非线性行为和大形变与三阶剪切形变理论(TSDT)比较接近。图4给出了用两种方法计算的复合层合板均方振速对比图,从图中可以看出两者具有较好的一致性。
图5为上述模型分别采用一阶剪切形变理论(FSDT)和三阶剪切形变理论(TSDT)计算的辐射声功率,由图可看出在600 Hz以下的频带内,两者辐射声功率级完全一致,这是因为在低频范围所分析波长远大于厚度,此时剪切形变和转动惯量对声辐射影响很小,随着频率的增加两者的差别开始增大,FSDT遗漏了较多的模态峰值,一方面是因为对于较厚的复合层合板高阶剪切应力和转动惯量会对声辐射起到一定作用,另一方面由于FSDT理论中剪切修正因子的选取差别也会带来一定的误差,这也进一步说明了TSDT理论能更准确地反映材料内部应力分布。
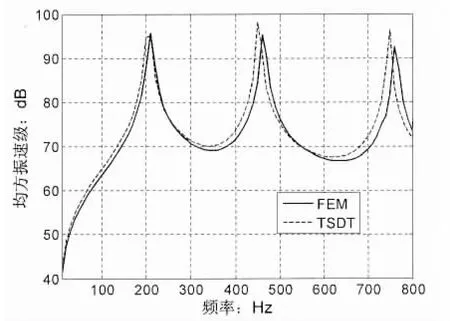
图4 模型均方振速验证Fig4 Validation of model mean square power of velocity
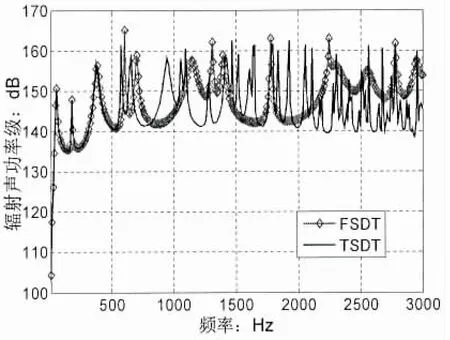
图5 FSDT与TSDT辐射声功率对比Fig 5 Comparison between the sound radiated FSDT and TSDT
3.2 参数分析
3.2.1 弹性模量对声辐射的影响
为了能简单而有效地说明弹性模量对声辐射的影响,取一单层正交各向异性复合板,厚度为0.006(m),铺层角度为45°,其余参数同上文一致。图6分析了材料参数E1、E2、G12和G13对声辐射的影响,由公式(9)和(10)可知这四个量将影响拉压刚度A、弯曲刚度D以及高阶刚度F、H等,因此其变化规律对声辐射的影响要远复杂于各向同性材料。从图中可看到在低频范围内(500 Hz以内),改变G12和G13对辐射声功率的影响很小,而改变E1和E2则有明显的频率峰值偏移,且峰值大小也有所改变。在中高频范围,改变E1、E2、G12和G13均会产生频率峰值偏移和大小改变,但是改变E1和E2,辐射声功率级大小变化在5 dB到10 dB左右,而改变G12和G13时辐射声功率级的起伏在5 dB以下。因此说,改变不同方向的杨氏模量E1和E2对声辐射的影响要大于改变剪切模量G12和G13对声辐射的影响,从整体上来说增加材料杨氏模量,系统的辐射声功率水平下降,这主要是影响了弯曲刚度,然而在某些区域随着杨氏模量增加反而会增加辐射声功率,因为杨氏模量的增加会改变其它刚度。剪切模量对中低频区域影响很小,仅在高频段有一定影响,这是因为在低频段剪切形变相对于分析波长可以忽略。
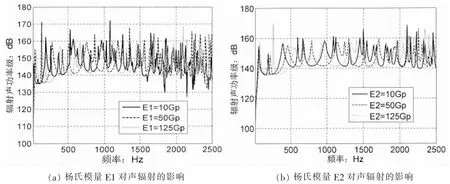
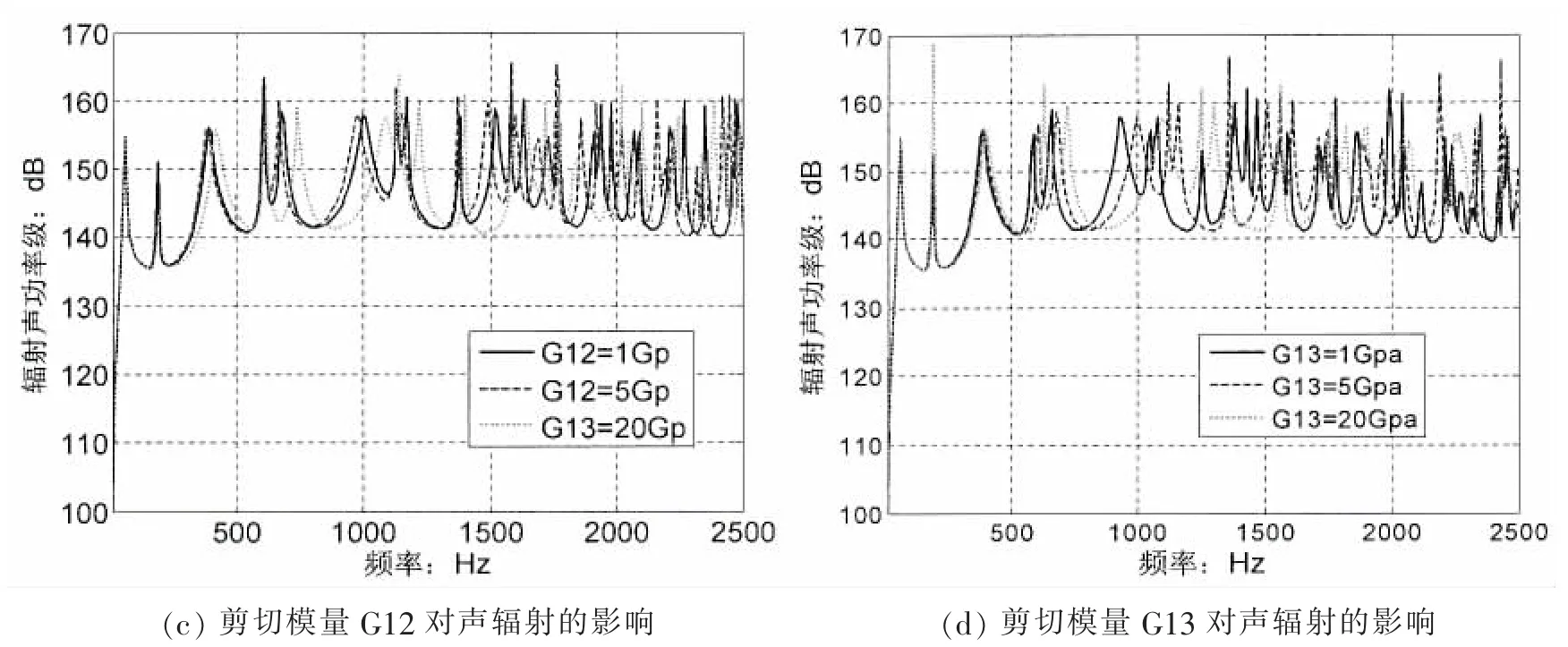
图6 材料参数对声辐射的影响Fig.6 Effects of material parameters to sound radiation
3.2.2 铺层厚度和铺设角对声辐射的影响
如图7所示,随着复合层合板厚度的增加,大部分频带内的辐射声功率级均有所下降,模态峰值存在频率偏移,且在中高频段能有效抑制掉部分谐振模态峰,这种厚度对声辐射的影响规律与均匀各向同性金属板是一致的,但由于复合层合材料的密度较金属板小很多,所以即使增加厚度也不会带来过多质量增加。因此增加复合层合板的厚度是有效降低辐射噪声的手段。
图8为纤维铺设角对声辐射的影响,由此可以看出声辐射随铺设角度的变化关系比较复杂,由(10)式可知,铺设角θ主要影响转换刚度系数,θ与各类刚度系数均有较复杂的关系,因此不能笼统的概括改变铺设角对声辐射的影响,整体而言45°时平均辐射声功率级较小,可以根据具体需要,在不同频段内对铺设角进行设计。
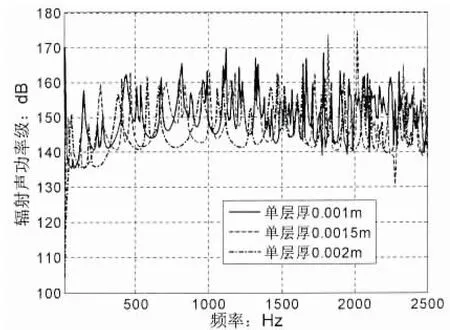
图7 铺层厚度对声辐射的影响Fig.7 Effects of lamina thickness
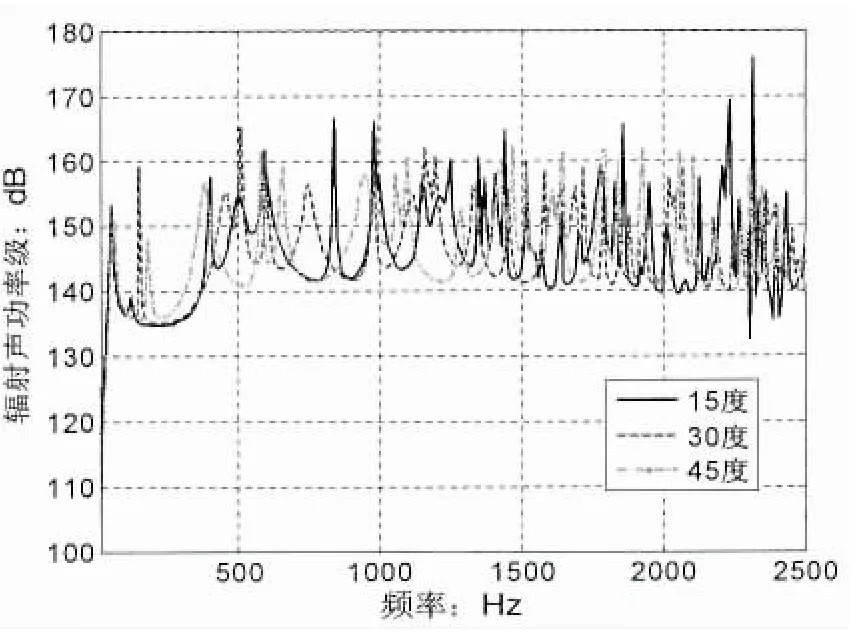
图8 纤维铺设角对声辐射的影响Fig.8 Effects of fiber orientation angle
4 结 论
本文利用三阶剪切形变理论,采用变分法建立和推导了较厚复合层合矩形板水下声辐射模型,通过与有限元法计算结果对比验证了所给算法的正确性,最后分析了不同参数对声辐射的影响,得到如下结论:
(1)由于要考虑高阶剪切和转动惯量,基于TSDT的复合层合板声辐射系统运动方程的推导要复杂于CLPT和FSDT,但利用表面应力自由条件可使系统运动方程维数与FSDT相同,且不需要剪切修正,在中高频率范围,采用TSDT的声辐射计算精度更高。
(2)材料参数对复合层合板声辐射的影响要远复杂于各向同性材料情况,杨氏模量E1和E2对声辐射的影响要大于剪切模量G12和G13,后者仅在高频段有影响。可以根据不同的设计要求,改变材料参数而实现噪声优化。
(3)复合层合板铺层厚度与铺设角是影响声辐射的重要参数,增加铺层厚度在大部分频段内能有效地降低辐射声功率级,而铺设角由于影响各类刚度转换系数对声辐射的影响规律较为复杂,45°时平均辐射声功率级较小。
[1]Qatu M S.Vibration of laminated shells and plate[M].Amsterdam:Elsevier Academic Press,2004.
[2]Berry A,Foin O,Szabo J P.Three dimensional elasticity model for a decoupling coating on a rectangular plate immersed in a heavy fluid[J].Journal of the Acoustical Society of America,2001,109(6):2704-2714.
[3]Yin X W,Gu X J,Cui H F,et al.Acoustic radiation from a laminated composite plate reinforced by doubly periodic parallel stiffeners[J].Journal of Sound and Vibration,2007,306:877-889.
[4]Ramachandran P,Narayanan S.Radiation efficiency of a composite cylindrical shell[C]//20th International Congress on Sound&Vibration.Bangkok,Thailand,2013.
[5]Mejdi A,Legault J,Atalla N.Transmission loss of periodically stiffened laminate composite panels:Shear deformation and in-plane interaction effects[J].Journal Acoustical Society of America,2012,13(1):174-185.
[6]杨 坤,梅志远,李华东.粘弹性复合材料夹芯板稳态响应分析[J].振动与冲击,2013,32(7):88-92. Yang Kun,Mei Zhiyuan,Li Huadong.Steady response analysis for a composite sandwich plate with viscoelastic core layer based on kelvin model[J].Journal of Vibration and Shock,2013,32(7):88-92.
[7]Lee S J,Reddy J N.Nonlinear deflection control of laminated plates using third-order shear deformation theory[J].International Journal of Mechanics and Materials in Design,2004,1:33-61.
[8]Ghinet S,Atalla N.Diffuse field transmission into infinite sandwich composite and laminate composite cylinders[J].Journal of Sound and Vibration,2006,289(4-5):745-778.
[9]吴 梵,杨 坤,梅志远,等.正交加筋复合材料夹层板弯曲问题求解[J].船舶力学,2013,17(1-2):92-101. Wu Fan,Yang Kun,Mei Zhiyuan.Bending solution of orthogonally rib-stiffened composite sandwich plate[J].Journal of Ship Mechanics,2013,17(1-2):92-101.
[10]Daneshjou K,Nouri A,Talebitooti R.Sound transmission through laminated composite cylindrical shells using analytical model[J].Arch Applied Mechanical,2007,77:363-379.
[11]Daneshjou K,Shokrieh M M,Moghaddam M G,et al.Analytical model of sound transmission through relatively thick FGM cylindrical shells considering third order shear deformation theory[J].Composite Structures,2010,93:67-78.
[12]Cao X T,Hua H X,Zhang Z Y.Sound radiation from shear deformable stiffened laminated plates[J].Journal of Sound and Vibration,2011,330(16):4047-4063.
[13]沈 苏,刘碧龙,李晓东,等.简支矩形板模态辐射阻抗的一种快速计算方法分析[J].声学学报,2010,35(2):126-133. Shen Su,Liu Bilong,Li Xiaodong.An analysis of a fast calculation method of modal radiation reactance of a simplysupported rectangular panel[J].ACTA Acustica,2010,35(2):126-133.
Sound radiation of underwater laminated composited rectangular plate using higher order shear deformation theory
HU Hao-haoa,b,GAO Yana,b
(a.National Key Laboratory on Ship Vibration&Noise;b.Jiangsu Key Laboratory of Green Ship Technology, China Ship Scientific Reaearch Center,Wuxi 214082,China)
Based on the simplified Third Order Shear Deformation Theory(TSDT),the vibration and sound radiation of moderate laminated composite rectangular plate were deduced,and the system motion equation was solved by Rayleigh-Ritz method.In order to validate the proposed method,the result was compared with the finite element method,and the advantage of calculating sound radiation was shown by comparing TSDT with FSDT.And by changing the Young’modulus,shear modulus,lamina thickness,fiber orientation angle,the main parameter and the variation in different frequency band were obtained,which could be a reference for underwater typical structure sound radiation and noise control.
third order shear deformation;laminated composite plate;sound radiation;noise control
TB535
:Adoi:10.3969/j.issn.1007-7294.2016.05.013
1007-7294(2016)05-0620-08
2016-02-27
国家自然科学基金资助项目(11274080)
胡昊灏(1983-)男,博士研究生,E-mail:huhaohao049@sohu.com;高 岩(1982-),女,高级工程师。

