基于裂纹最大张口位移的加筋板弹塑性断裂分析

邓军林，杨 平，唐卫国，汪 丹

（1.高性能船舶技术教育部重点实验室（武汉理工大学），武汉 430063；2.武汉理工大学 交通学院，武汉 430063）

基于裂纹最大张口位移的加筋板弹塑性断裂分析

邓军林1，2，杨 平1，2，唐卫国2，汪 丹2

（1.高性能船舶技术教育部重点实验室（武汉理工大学），武汉 430063；2.武汉理工大学 交通学院，武汉 430063）

为了快速方便地求取船舶加筋板塑性性能的两个重要参数—裂纹尖端塑性区半径（Ry）和裂纹尖端张开位移（CTOD），文章提出了一种基于裂纹最大张口位移（MCOD）来确定加筋板的裂纹尖端塑性区半径和裂纹尖端张开位移的简便方法。该法基于理想弹塑性材料，以提出的裂纹最大张口位移与裂纹尖端塑性区半径及裂纹尖端张开位移的拟合函数关系为基础，考虑了模型尺寸效应、材料特性参数及外载荷的影响。文中还对不同裂纹长度、不同屈服极限条件、不同板/筋刚度比时方法的适用性进行了分析，研究表明：该方法能够消除裂纹长度、屈服极限和外载荷等因素的影响，适用于有限宽船舶加筋板的弹塑性分析。

船舶加筋板；CTOD；裂纹最大张口位移；裂纹尖端塑性区半径；弹塑性

0 引 言

加筋板结构是船舶和海洋工程结构领域最基本的结构之一。近年来，随着船舶结构大型化的发展及高强度钢的广泛使用，含裂纹的船舶加筋板结构发生断裂破坏时大多已经处于弹塑性状态。然而到目前为止，对加筋板断裂性能方面的研究工作大多局限于线弹性范围。如：Sabelkin[1-2]对含裂纹有限加筋板尺寸及边界条件对应力强度因子的影响进行了研究；黄海燕等[3-5]对含中心穿透裂纹的有限加筋板的应力强度因子进行了分析；姜翠香[6]采用直接法对含中心穿透裂纹有限宽加筋板进行了弹塑性初步分析，但没有对相应影响因素做进一步的研究。陈景杰[7-8]率先基于最大张口位移对裂纹板中体现塑性断裂性能的两个重要参数进行了研究分析，本文在其基础上考虑筋条不同刚度比对含中心穿透裂纹加筋板弹塑性断裂性能影响进行了研究。

在弹塑性断裂力学中，目前大多以裂纹尖端张开位移（CTOD）和裂纹尖端塑性区半径Ry作为描述裂纹塑性性能的主要参数。裂纹尖端塑性区对裂纹的萌生、扩展起着决定性的作用；裂纹尖端张开位移（CTOD）是判定裂纹在弹塑性范围内扩展的重要准则，被定义为材料的弹塑性断裂韧性。基于已有的确定CTOD和Ry的各种方法可知：有限元数值计算是研究它们的重要手段。

裂纹最大张口位移 （Δu）（为方便表达，文中用Δu表示MCOD）是描述裂纹形状的主要变量，而且无论是在有限元计算还是实验测量中都相对容易获得，因此，本文引入了Δu的概念。首先通过有限元模拟计算建立了具有中心穿透裂纹的无限大加筋板模型在特定条件下Δu与含中心穿透裂纹加筋板的CTOD和Ry之间的函数关系，然后考虑模型尺寸、材料特性（屈服强度、应力状态等）、裂纹长度和外载荷等因素影响效应，确定相应函数关系式的适用范围。该法回避了对裂纹尖端局部区域的直接分析，使有限元计算模型得到简化，并为含中心穿透裂纹加筋板CTOD和Ry的实际测量提供了新的途径。

1 理论分析

1.1 裂纹尖端塑性区半径与裂纹最大张口位移关系

在小范围屈服条件下，对于理想弹塑性材料，陈景杰[7]在Irwin的估算公式[9]基础上研究推导出了中心穿透裂纹的无限大板在单向拉伸载荷作用下的裂纹尖端塑性区半径Ry为：

式中：σs为材料屈服极限，μ为泊松系数，a为裂纹长度，σ为外加均匀载荷。

该表达式表明Ry与外载荷、裂纹长度及屈服极限间的对应关系。当裂纹长度和屈服极限为确定的常数时，Ry与外载荷σ间一定存在某种函数对应关系：

根据已有的当等效裂纹长度为2a+Ry时的小范围塑性屈服问题可采用线弹性理论进行分析的结论，结合文献[7]所给出的最大张口位移与外力及裂纹长度的关系式，可等效表达为：

与无限大板类似，由（2）、（3）式可以得出在小范围塑性屈服状况下，含有中心穿透裂纹的无限大船舶加筋板在单向拉伸载荷作用下Δu与Ry间也一定存在某种相应的函数对应关系：

1.2 裂纹尖端张开位移与裂纹最大张口位移关系

对于理想弹塑性材料，在外力σ小于等于屈服极限σs的条件下，姜翠香[6]在Dugdale[10]模型基础上对承受单向拉伸载荷作用的含有中心穿透裂纹的无限大加筋板进行了研究并给出了加筋板裂纹尖端张开位移CTOD的近似计算公式：

式中：f0为修正函数，G为剪切模量。

同理，在确定的平面状态下，当裂纹长度和屈服极限一定时，同样可以得出含有中心穿透裂纹的无限大船舶加筋板在单向拉伸载荷作用下裂纹尖端张开位移δ与裂纹最大张口位移Δu间存在某种对应的函数关系：

只要确定出公式（4）、（6）的具体表达式，通过有限元法求出加筋板裂纹最大张口位移，就可以快捷地对含有中心穿透裂纹的无限大船舶加筋板裂纹尖端的塑性区半径Ry及裂纹尖端张开位移δ进行评估，从而为在外力作用下快速评估加筋板结构的弹塑性性能提供了捷径。

2 计算模型精度的确定

2.1 裂纹尖端塑性区及裂纹尖端张口位移模型计算精度的确定

船舶加筋板有限元计算模型如图1所示，2W为裂纹板宽度，2L为裂纹板长度，2a为裂纹长度，σ为外力；选取a=10 mm，L=15a和W=13a及分别选取加筋条不同刚度比β=EsAs/EBt0=0.1，0.2，0.3（Es为加筋条弹性模量，As为加筋条横截面积）来模拟无穷大船舶加筋板。材料参数：E=2.1×105MPa，泊松比ν=0.3。在平面应力状态下，σ取10～200 MPa范围内每间隔10 MPa的应力值进行弹塑性分析。在进行有限元分析过程中，取材料屈服极限为235 MPa，采用理想弹塑性材料的应力应变曲线，结合随动强化和Mises屈服准则计算裂纹尖端塑性区，其1/4含中心穿透裂纹加筋板有限元模型及其局部单元网格划分如图2所示。

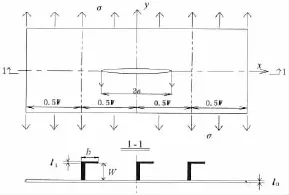
图1 含中心穿透裂纹的船舶加筋板拉伸试样Fig.1 A ship stiffened plate with central through-cracks and the stress distribution models

图2是基于Ansys有限元软件采用8节点的四边形等参单元所建立的加筋板中含中心穿透裂纹的加筋板材有限元模型。其裂纹尖端区域的最小单元尺寸为0.05 mm，它所对应的外加应力为50 MPa。由于网格尺寸直接影响塑性区半径计算精度，所给定的最小单元尺寸是根据已有剖分准则确定的[4]。

图3给出了不同外载荷下有限元法与Irwin公式法计算的裂纹尖端塑性区半径大小。在小范围屈服内（σ/σs≤0.3）两种方法计算的塑性区半径十分接近，表明在小范围屈服内有限元法计算的塑性区尺寸是正确可靠的，证明了有限元计算模型的可靠性。

采用有限元法直接计算加筋板裂纹尖端张开位移同样也需要对加筋板裂纹尖端局部区域划分精细网格单元，本文在分别确定描述裂纹尖端塑性区性能的这两个参数时采用相同的有限元计算模型。另外，通过有限元法计算CTOD时通常取裂纹尖端45°斜线与上下裂纹面相交的交点间的垂直距离[11]或以裂纹面上与裂纹尖端最近节点的法向张开位移作为裂纹尖端的张开位移[12]。本文中计算裂纹尖端张开位移的步骤为：首先根据有限元法计算加筋板裂纹面上各单元节点的张开位移，采用路径法确定出加筋板裂纹表面各单元节点的位移变形图，然后将加筋板裂纹表面各单元节点张开位移的转折点对应的法向位移的两倍确定为裂纹尖端张开位移[7]。

图2 含中心穿透裂纹加筋板有限元1/4有限元模型Fig.2 Quarter of finite element models for stiffened platewith central through crack

图3 Irwin公式法与有限元法计算的加筋板 裂纹尖端塑性区半径的比较Fig.3 Comparison of plastic zone radiu of stiffened plate calculated by finite element and Irwin’s formula

2.2 最大张口位移计算精度的确定

为了保证求解加筋板裂纹最大张口位移（Δu）的有限元模型计算结果的可靠性，本研究对含中心穿透裂纹的加筋板采用有限元法求得的最大张口位移收敛性进行了验证。计算裂纹最大张口位移（Δu）的有限元模型同图2所示。

图4 加筋板裂纹尖端最大张口位移收敛性验证Fig.4 Convergence judgment of crack maximum opening displacement of stiffened plate

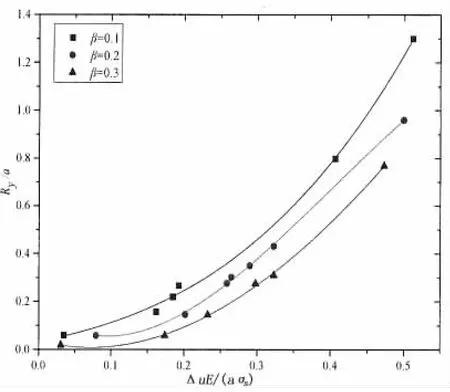
图5 加筋板Ry/a和ΔuE/aσs之间的对应关系曲线Fig.5 Relationship of stiffened plate between Ry/a versus ΔuE/aσs

利用有限元法计算平面应力状态下加筋板裂纹最大张口位移（Δu）随裂纹尖端网格不断细化的变化情况如图4所示，其中i为计算模型的节点数量。图4显示出加筋板Δu随模型单元节点数的增加而逐渐趋于稳定，说明加筋板有限元模型计算的裂纹Δu是收敛的，可以保证加筋板裂纹最大张口位移计算结果的可靠性。根据图4计算结果并考虑有限元法计算精度和效率，本文选取总单元节点数为14 450对应的有限元模型计算含中心裂纹的加筋板Δu数值。

3 确定加筋板裂纹尖端塑性区半径与裂纹最大张口位移的函数关系

针对图3给定的外载荷计算出无限宽含中心穿透裂纹加筋板对应的Δu值，将Ry和Δu值进行标准化处理得到对应的无量纲参数Ry/a和ΔuE/aσs值。基于最小二乘法原理，建立Ry/a和ΔuE/aσs间多项式拟合曲线，确定了无限宽加筋板模型Ry/a和ΔuE/aσs间对应的函数关系，如图6所示。由于已建立的拟合函数关系式是无限宽的加筋板在理想弹塑性材料状态下求得，为满足工程实践的需要，故需要讨论含中心穿透裂纹加筋板的尺寸效应、材料参数以及载荷因素等对其的影响，并最终确定出满足实际工程需要的含中心穿透裂纹加筋板Ry/a和ΔuE/aσs对应函数关系表达式的适用范围。

3.1 模型尺寸和外加载荷的影响

考虑模型尺寸和外加应力对加筋板Ry/a和ΔuE/aσs间拟合函数关系的影响时，在图5所示的模型中选取a=10 mm，L=150 mm，a/W=0.05～0.5；筋条刚度比β=EsAs/EBt0=0.1，0.2，0.3，外应力σ分别为40、60、80、100 MPa。在材料参数保持不变（E=2.1×105MPa，泊松比ν=0.3，σs=235 MPa）的情况下，采用理想弹塑性材料并选取MISES屈服准则，建立系列有限元模型并分别计算对应Δu和裂纹尖端塑性区半径Ry，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图5的关系表示如图6所示。

图6 不同W和σ下加筋板Ry/a和ΔuE/aσs之间的函数关系曲线Fig.6 Relationship of stiffened plate between Ry/a versus ΔuE/aσsin the case of different W and σ

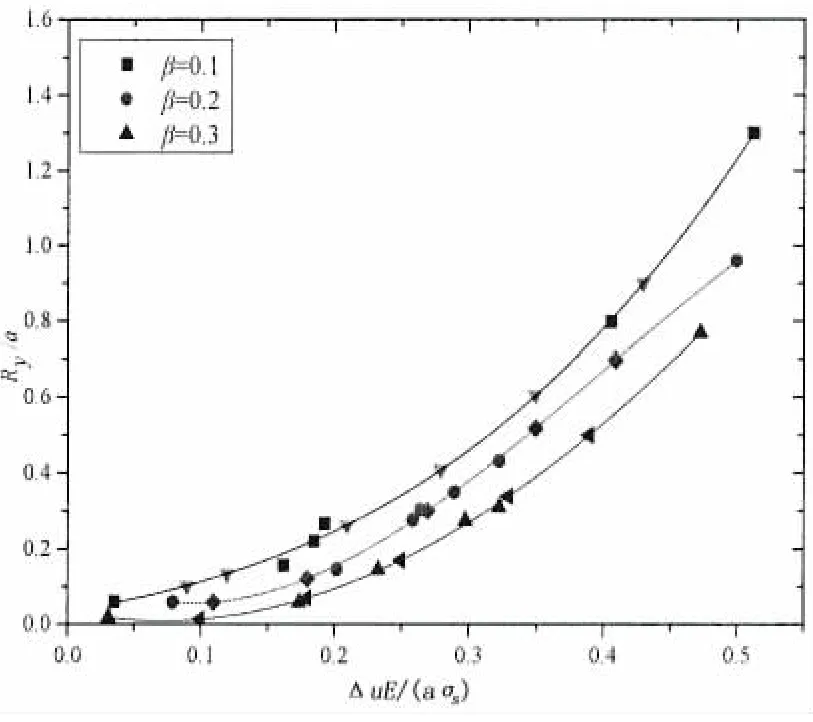
图7 不同a和σs下加筋板Ry/a和ΔuE/aσs之间的函数关系曲线Fig.7 Relationship of stiffened plate between Ry/a versus ΔuE/aσsin the case of different a and σs

图6表明：不同外载荷作用下任意宽度的含中心穿透裂纹加筋板所获得的标准化的计算结果具有相同函数关系，说明Ry/a和ΔuE/aσs之间的函数关系与加筋板宽度和外应力无关，用裂纹最大张口位移计算加筋板裂纹尖端塑性区半径的方法消除了宽度和外应力的影响。

3.2 裂纹长度和屈服强度的影响

考虑裂纹长度和屈服强度对加筋板Ry/a和ΔuE/aσs间拟合函数关系的影响时，计算模型保持不变，选取L=150 mm，W=50 mm，a=10～20 mm，σs分别为235、255（25）400 MPa，σ=20～100 Mpa，筋条刚度比β=EsAs/EBt0=0.1，0.2，0.3。在弹性模量E和泊松比ν保持不变的情况下，建立系列有限元模型分别计算对应的Δu和裂纹尖端塑性区半径值Ry，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图5的关系表示如图7所示。

图7表明：在不同裂纹长度和屈服极限条件下所确定的有限宽度的船舶加筋板Ry/a和ΔuE/aσs值几乎近似布落在已获得的关系曲线上，说明用裂纹Δu计算加筋板裂纹尖端塑性区半径排除了裂纹长度和屈服极限的影响。

3.3 平面状态和材料弹性模量的影响

研究材料弹性模量对函数关系的影响时，计算模型保持不变，在图1所示的模型中选取，a=10 mm，L=150 mm，W=6a，σ=40～70 MPa，筋条刚度比β=0.1，0.2，0.3。弹性模量E在48～210 GPa范围内变化，其它材料参数保持不变的情况下，建立系列有限元模型分别计算对应的裂纹最大张口位移Δu和裂纹尖端塑性区半径值Ry，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图5的关系表示如图8所示。

图8 不同E计算结果与已有函数关系曲线的关系Fig.8 Relationship of stiffened plate between resuilts and obtained function curve in different E

图9 平面应变状态计算结果与已有函数关曲线的关系Fig.9 Relationship of stiffened plate between resuilts and obtained function curve in the plane strain

以上结果均是在平面应力状态下计算得到的，考虑平面应变状态对加筋板Ry/a和ΔuE/aσs间拟合函数关系的影响时计算模型和外加载荷保持不变，得到了平面应变状态下Ry和Δu的标准化结果如图9所示的数据点。

图8和图9表明：不同弹性模型和平面状态下计算得到的加筋板Ry/a和ΔuE/ aσs的数值结果几乎都分布在已有的函数关系曲线上，说明无量纲化处理加筋板裂纹尖端塑性区半径Ry和裂纹最大张口位移Δu的数值结果消除了弹性模量和平面状态的影响。

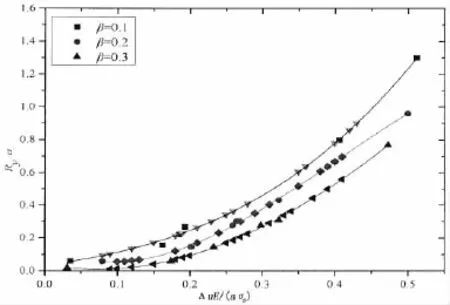
图10 所有给定情况下加筋板Ry/a和ΔuE/aσs之间的函数关系Fig.10 Relationship of stiffened plate betweenRy/a versus ΔuE/aσsin all given case

综上，为了更直接说明上述6个因素对函数关系的影响，将图5～9中计算所得的数据整理到同一坐标图中如图10所示。这些数据根据加筋板不同刚度比布落在相应的同一条曲线上，说明基于最小二乘法拟合出的加筋板Ry/a和ΔuE/aσs间的函数关系式（7）消除了模型尺寸、裂纹长度、外应力、材料屈服极限、弹性模量及平面状态的影响。

4 确定加筋板CTOD与裂纹最大张口位移的函数关系

针对图3给定的外应力计算出无限宽含中心穿透裂纹加筋板对应的Δu值，将δ和Δu值进行标准化处理得到对应的无量纲参数δE/aσs和ΔuE/aσs值。基于最小二乘法原理，建立δE/ aσs和ΔuE/aσs间多项式拟合曲线，确定了无限宽加筋板模型两者之间对应的函数关系，如图11所示。由于已建立的拟合函数关系式是无限宽的加筋板在理想弹塑性材料状态下求得，为满足工程实践的需要，故需要讨论含中心穿透裂纹加筋板的尺寸效应、材料参数以及载荷因素等对其的影响，并最终确定出满足实际工程需要的含中心穿透裂纹加筋板δE/aσs和ΔuE/aσs对应函数关系表达式的适用范围以满足实际工程应用。

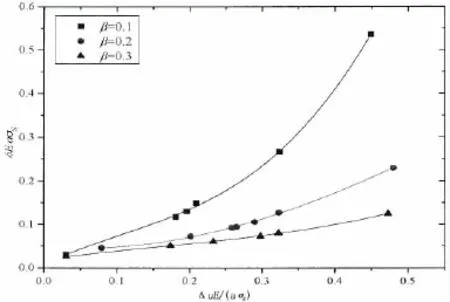
图11 加筋板δE/aσs和ΔuE/aσs之间的对应函数关系曲线Fig.11 Relationship of stiffened plate between δE/aσsversus ΔuE/aσs

4.1 模型尺寸和外加载荷的影响

考虑模型尺寸和外加载荷对加筋板δE/aσs和ΔuE/aσs间拟合函数关系的影响时，选取a=10 mm，L=150 mm，a/W=0.05～0.5；筋条刚度比β=0.1（0.1）0.3，外应力σ分别为40（20）100 MPa。在材料参数保持不变的情况下，建立系列加筋板有限元模型分别计算对应裂纹最大张口位移Δu和裂纹尖端张开位移δ，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图11的关系如图12所示。

图12 不同W和σ下加筋板δE/aσs和ΔuE/aσs之间的函数关系曲线Fig.12 Relationship of stiffened plate between δE/aσsversus ΔuE/aσsin the case of different W and σ

图13 不同a和σs下加筋板δE/aσs和ΔuE/aσs之间的函数关系曲线Fig.13 Relationship of stiffened plate between δE/aσsversus ΔuE/aσsin case of different a and σs

图12表明：不同外载荷作用下任意宽度的含中心穿透裂纹加筋板所获得的标准化的计算结果具有相同函数关系，说明加筋板δE/aσs和ΔuE/aσs间的函数关系与加筋板宽度W及外力无关，用裂纹最大张口位移Δu确定加筋板裂纹尖端张开位移δ的方法消除了加筋板宽度W及外力的影响。

4.2 裂纹长度和屈服强度的影响

考虑裂纹长度和屈服强度对加筋板δE/aσs和ΔuE/aσs间拟合函数关系的影响时，计算模型保持不变，在图1所示的模型中选取L=150 mm，W=50 mm，a=10～20 mm，筋条刚度比β=0.1，0.2，0.3，分别为235、255（25）400 MPa，σ=20～100 MPa。在材料参数保持不变的情况下，建立系列加筋板有限元模型分别计算对应的裂纹Δu和裂纹尖端张开位移δ，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图11的关系表示如图13所示。

图13表明：在不同裂纹长度和屈服极限条件下所确定的加筋板δE/aσs和ΔuE/aσs数值几乎都落在已获得的函数关系曲线上，说明基于裂纹Δu确定加筋板裂纹尖端张开位移δ的方法消除了裂纹长度和材料屈服极限的影响。

4.3 平面状态和材料弹性模量的影响

研究材料弹性模型对加筋板δE/aσs和ΔuE/aσs间拟合函数关系的影响时，计算模型保持不变，在图1所示的模型中选取，a=10 mm，L=150 mm，W=6a，σ=40～70 MPa，筋条刚度比β=0.1，0.2，0.3。弹性模量E在48～210 GPa范围内变化，其它材料参数保持不变的情况下，建立系列有限元模型分别计算对应的裂纹最大张口位移Δu和裂纹尖端张开位移δ，根据选定的无量纲化参数，标准化处理计算得到的数据值并将得到的无量纲化结果与图11的关系表示如图14所示。

图14 不同E计算结果与已有函数关系曲线的关系Fig.14 Relationship of stiffened plate between resuilts and obtained function curve in different E

图15 平面应变状态计算结果与已有函数关系曲线的关系Fig.15 Relationship of stiffened plate between resuilts and obtained function curve in the plane strain

以上结果均是在平面应力状态下计算得到的，下文给出了平面应变状态下计算模型在外加应力为10～210 MPa作用下的计算结果，得到了平面应变状态下加筋板δ和Δu的标准化结果如图15所示的数据点。

图14和图15表明：不同弹性模型和平面状态下计算得到的加筋板δE/aσs和ΔuE/aσs数值结果几乎都落在已有的函数关系曲线上，说明无量纲化处理加筋板裂纹尖端张开位移δ和裂纹Δu消除了弹性模量和平面状态的影响。

综上，为了更直接说明上述6个因素对加筋板δE/aσs和ΔuE/aσs间拟合函数关系的影响，将图11～15中计算所得的数据整理到同一坐标图中如图16所示。这些数据根据加筋板不同刚度比分布在相应的同一条曲线上，说明基于最小二乘法拟合出的加筋板δE/aσs和ΔuE/aσs间的函数关系式（8）消除了模型尺寸、裂纹长度、外载荷、材料屈服极限、弹性模量及平面状态的影响。

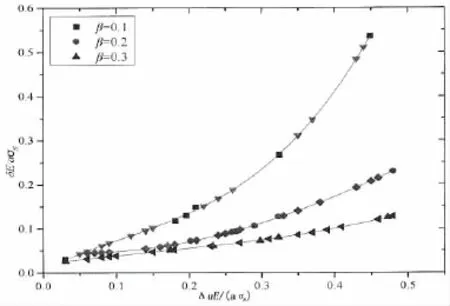
图16 所有给定情况下加筋板δE/aσs和ΔuE/aσs之间的函数关系Fig.16 Relationship of stiffened plate between δE/aσsversus ΔuE/aσsin all given case

5 结 论

本文通过理论分析和有限元数值模拟，对描述具有中心穿透裂纹的有限宽加筋板裂纹尖端弹塑性断裂性能的两个重要参数Ry和CTOD进行了分析并得到了如下结论：

（1）通过对受单向拉伸载荷作用的含有中心穿透裂纹的船舶加筋板模型的计算分析，提出了加筋板Δu与Ry的无量纲参数及其对应的考虑不同筋条刚度比的多项式函数关系；讨论了裂纹长度、模型尺寸、外载荷、屈服极限及应力状态等因素的影响，明确了能体现筋条不同刚度比影响的加筋板Ry/ a和ΔuE/aσs间拟合函数关系式的适用范围，使其满足工程应用。

（2）通过对受单向拉伸载荷作用的含有中心穿透裂纹的船舶加筋板模型的计算分析，建立了加筋板Δu与CTOD的无量纲参数及其对应的考虑不同筋条刚度比的多项式函数关系；讨论了模型尺寸、裂纹长度、外加载荷、屈服极限及应力状态等因素的影响，明确了能体现筋条不同刚度比影响的加筋板δE/aσs和ΔuE/aσs间拟合函数关系的适用范围。

[1]Sabelkin V,Mall S,Avram J B.Fatigue crack growth analysis of stiffened cracked panel repaired with bonded composite patch[J].Engineering Fracture Mechanics,2006(73)：1553-1567.

[2]Tsamasphyros G,Dimou G.Stress intensities in a strip reinforced by stiffeners at the edges[J].Engineering.Fracture Mechanics,1995,51(6)：897-914.

[3]黄海燕,刘小健.含中心裂纹有限加筋板应力强度因子的计算精度评估[J].船舶力学,2008,12(5)：765-769. Huang haiyan,Liu xiaojian.Accuracy evaluation of stress intensity factor about stiffened plate with a central crack[J].Journal of Ship Mechanics,2008,12(5)：765-769.

[4]Liu Rong,Zhang Tie,Wu X J,Wang C H.Detemination of stress intensity factors for a cracked shell under bending with improved shell theories[J].Journal of Aerospace Engineering,2006(1)：21-28.

[5]Garcia-Manrique J,Camas D.Stress intensity factors analysis of through thickness effects[J].International Journal of Fatigue,2013,46：58-66.

[6]姜翠香,赵 耀.含中心裂纹的有限加筋板Dugdale模型[J].中国造船,2004,45(1)：65-71. Jiang cuixiang,Zhao yao.Dugdale model analysis on finite internally cracked plate with stiffened edges[J].Shipbuliding of China,2004,45(1)：65-71.

[7]陈景杰.含裂纹损伤船体结构强度分析方法研究[D].大连：大连理工大学,2011. Chen jingjie.Strength analysis method research of cracked ship structure[D].Dalian：Dalian University of Technology, 2011.

[8]Huang Yi,Chen Jingjie,Liu Gang,et al.A new method of crack-tip opening displacement determined based on maximum crack opening displacement[J].Eng.Fract.Mech.,2011,78(7)：1441-1451.

[9]Irwin G R,Plastic zone near a crack and fracture toughness[C]//Proc.Sagamore Res.Conf.Mech.Metals Behabavior Sheet Mater.New York,1995,71(1)：57-69.

[10]Chen Y Z.A Dugdale problem for a finite internally cracked plate[J].Fracture Mech,1983,7(6)：579～583.

[11]Ostby E,Thaulow C,Bard N.A new approach to ductile tearing assessment of pipelines under large-scale yielding[J]. Int.J Pres.Ves.Pip.,2007,84：337-348.

[12]Yaowu S,Siying S,Hidekazu M,et al.Finite element analysis on relationships between the J-integral and CTOD for stationary cracks in welded tensile specimens[J].Int.J Pres.Ves.Pip.,1998,75：197-202.

Elasto-plastic fracture analysis of stiffened plates based on crack maximum opening displacement

DENG Jun-lin1,2,YANG Ping1,2,TANG Wei-guo2,WANG Dan2
(1.Key Laboratory of High Performance Ship Technology(Wuhan University of Technology)，Ministry of Education, Wuhan 430063,China;2.School of Transportation,Wuhan University of Technology,Wuhan 430063,China)

In order to rapidly and conveniently evaluate the two important plastic property parameters of ship stiffened plate,i.e.the plastic-zone radius around crack tip and crack tip opening displacement(CTOD), a simple method is proposed for ship stiffened plates with central-through crack subjected to uniform uniaxial tensile loading,based on the maximum crack opening displacement(MCOD).On the basis of the fitted functional relationship of the MCOD and the two plastic property parameters,the influences of the model size effect,material parameters and external load are discussed in the analyses for elastic-perfectly plastic material.The applicability of this method for different crack length,yield limit condition and stiffness ratio of plate/stiffener was analyzed.The result from this research shows that the presented method can eliminate the influence of the crack length,yield stress and applied loading etc,and so is suitable to the elasto-plastic analysis for ship stiffened plates with finite width.

ship stiffened plate;crack tip opening displacement(CTOD);maximum crack opening displacement(MCOD);plastic-zone radius around crack tip;elasto-plastic

U661.41

：Adoi：10.3969/j.issn.1007-7294.2016.05.008

1007-7294（2016）05-0574-09

2015-10-15

国家自然科学基金面上项目（51479153），中央高校研究生自由探索研究项目（2014-zy-019）

邓军林（1983-），男，博士研究生，E-mail：junlin.deng@163.com；杨 平（1955-），男，教授，博士生导师。