预测信息传播中的转发选择
王永庆, 沈华伟, 程学旗
(中国科学院 计算技术研究所网络数据科学与技术重量实验室,北京 100190)
预测信息传播中的转发选择
王永庆, 沈华伟, 程学旗
(中国科学院 计算技术研究所网络数据科学与技术重量实验室,北京 100190)
在信息传播中,用户在重复接收同一信息的情况下其转发行为会具有一定的倾向性。对这种转发的倾向性建模是影响力分析、传播动力学、社会推荐等一系列信息传播相关应用研究领域中的一个关键问题。本文假设用户的转发选择行为主要由用户间的人际影响力决定。人际影响力的大小由信息传播者的影响力和信息接收者的易感性共同作用。本文从真实的信息传播记录中推断出用户隐式的影响力和易感性,进而提出了一种转发选择模型。该模型能够有效解决目前方法存在的对转发选择行为建模不充分和模型泛化能力差的问题。本文选取典型的转发选择建模方法作为比较,将所提的转发选择模型在新浪微博数据上进行对比验证。实验表明,本文所提的模型在两种评价指标上均取得更好效果,证明了所提模型的有效性。
信息传播;转发选择;影响力;易感性
1 引言
社会媒体(Social media)的诞生极大提高了人们获取和传递信息的能力。例如通过博客、论坛、微博、百科等平台,用户利用互动式的交流和表达方式,使得信息经由用户的社会关系有序传播。在这种信息传播中,社会媒体用户能够有较多机会通过其社交关系重复接收同一信息: 一方面加深用户对该信息的认识使得用户有更高的概率对该信息进行转发;另一方面,用户必须从多个信息源的转发中做出转发选择。现有文献表明,用户的转发选择行为具有一定的倾向性。一般而言,这种转发选择行为被视作是人际影响力的直接体现[1- 2]。因此如何理解用户在转发选择时的行为倾向,是研究人际影响力的切入点之一,建模并预测转发选择行为也是影响力分析[3]、传播动力学[1, 4]、社会推荐[5]等一系列信息传播相关应用研究领域中的一个关键问题。
现有尝试对用户人际影响力进行建模的方法可大致分为三类: 利用网络结构,利用历史传播记录信息和利用用户传播属性的建模。利用网络结构的影响力分析主要是从度分布(degree distribution)[6],聚集系数(clustering coefficient)[7],连接强度(tie strength)[8],介数(betweenness)[9],中心度度量(centrality)[10-11]等网络的物理性质上进行讨论。在利用历史传播记录信息的影响力建模方面,Tang等人[12]提出了综合主题模型(topic model)及传播记录的建模方式,在引文网络中较好识别了各话题下的代表性人物及发表论文。Gomez等人[13]提出了基于生存模型的建模方法,该方法假设用户在一次信息传播的过程中,不断地被周围新“感染”的邻居影响,直至最终转发消息。Myers[14]等人提出了针对外部消息源影响力的建模方法,并较好拟合了信息传播的爆发曲线。在利用用户传播属性建模方面,Saito等人[15]提出了显式的用户属性建模方法,估计用户个体间的信息传播概率,并预测信息的传播发生情况。Cui等人[16]提出了隐式的用户及文档属性建模方法,并用于推断用户对影响用户的偏好以及用户对内容的偏好问题。以上所述方法利用了对人际影响力的不同认识,部分解释了信息传播中的现象,但仍无法较好解决主要由人际影响力所导致的转发选择问题。所存在的主要问题有: 1)基于网络分析的方法忽略了平台本身的异质性,这类分析方法无法保证某一网络的物理性质与存在传播现象之间存在关联的普适性,因果分析不够准确; 2)基于历史传播记录信息的建模方法目前还没有较好泛化能力,只能就观测节点对间的传播情况进行推断及预测,缺失大量节点对间的传播记录信息会使得该分类中的建模方式失效。3)大量的传播及用户数据以匿名化的方式存在,这使得显式的用户传播属性较难获得。并且目前没有较为系统的研究工作支持人际影响力与用户传播属性之间的关系。
为了避免上述问题,有效建模信息传播中用户的转发选择行为,本文提出了转发选择模型(Forwarding-Preference Model,FPM)。FPM模型能够对隐式的用户传播属性进行建模,将用户传播属性按照用户在信息传播中的传播者及接收者角色分为影响力(influence)及易感性(susceptibility)属性[17]。在信息传播过程中,传播者与接收者间的人际影响力由传播者的影响力向量和接收者的易感性向量的内积确定。用户的转发选择行为是信息接收者以较高概率选择对其更具影响力的传播者的选择过程。目前而言,这种从人际影响力角度对转发选择行为的建模工作是一个较新的信息传播应用问题。本文形式化了转发选择问题,并对该应用问题给出了一种建模求解的方法。FPM模型的优势在于:
1) FPM模型有较好的泛化能力。所推断隐式的用户影响力与易感性属性与用户节点相关,与用户间的连边无关。对于缺失的节点对间的传播记录信息,其人际影响仍可通过节点与其他节点的历史交互推断获得。
2) FPM模型是对人际影响力导致的用户转发选择行为的直接建模,量化并推断人际影响力。通过实际数据的验证表明,本文所提模型与原有估计方法相比在评价指标上具有较大幅度的提升。表明了人际影响力与用户转发选择行为之间存在相关性,并证实了所提模型的有效性。
3) 相比建模用户显式的传播属性,FPM模型所推断的隐式用户传播属性仅需历史传播记录信息,受数据获取的限制更少,这使得所提模型具有较好的适用性。
本文设计了迭代算法,通过所观测的用户转发偏好,学习获得用户隐式的影响力及易感性属性。在实验部分,在新浪微博数据上对FPM模型及所选典型的比较方法进行评测。实验结果表明,FPM模型能够在本文所给定的两个评价标准上均取得较为显著的预测性能提升,模型对用户转发选择行为的建模是有效的。
文章的后续部分组织如下: 第二章是相关工作的介绍;第三章形式化和建模用户由人际影响力所产生的转发选择过程,给出FPM模型,并给出对应的学习算法。第四章对实验数据、评价指标、对照方法以及比较结果进行介绍及说明。最后在第五章中给出本文的结论。
2 相关工作
对用户在信息传播中的转发选择行为建模和推断的工作是目前信息传播领域一个新的应用研究问题。对该问题的认识,目前主要认为用户在信息传播中的转发选择行为主要由人际影响力所决定。大量的相关工作主要集中于用户在信息传播中的传播动力学研究。
信息传播动力学的相关实证研究工作利用统计规律发现信息传播的相关因素和因果联系。Romero等人[18]利用在Twitter上医药信息的传播记录发现,信息传播相较于疾病传播是一种更为复杂的传播方式。与疾病传播不同,用户在同一信息下暴露多次时会产生明显的边际效应。Leskovec等人[4]研究了病毒式营销市场的传播动力学,揭示了信息传播与其他传播系统的不同,并初步探讨了影响信息传播的用户属性。Huang等人[5]通过豆瓣数据实证了用户评价对其他用户评分的影响,证明病毒式营销市场中用户之间影响力的确实存在。Gruhl等人[19]通过博客数据分别从宏观的话题层次与微观的用户层次对信息传播的动力学进行探讨,并提出了基于宏观与微观层次的影响力模型。Leskovec[20]利用博客关系图及图上的传播模式模拟博客空间中的信息传播。Ugander等人[1]在Twitter数据中分析了传播网络的结构特征,揭示了传播网络的结构多样性与信息传播之间的联系。Crane等人[21]度量了信息传播中触发评论行为的內源及外源因素。Bao等人[2]证实了信息传播中的累积效应(cumulative effects),并利用传播网络的结构分析方法对用户的转发选择进行了初步探索。Tang等人[12]结合话题与社会网络,建模了话题相关的影响力模型,并在引文网络中进行验证。Aral等人[3]引入了影响力与易感性两种传播属性的度量方式,利用Twitter数据对信息传播中用户传播属性的分布进行了实证研究。Cui等人[16]建模了文档层次的人际影响力模型,提出了用户与文档的相关隐属性向量。这些工作在一定程度上给予我们对信息传播动力学的理解,启发我们对转发选择行为的建模工作。
3 转发选择行为建模
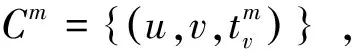

表 1 符号及对应描述
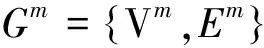
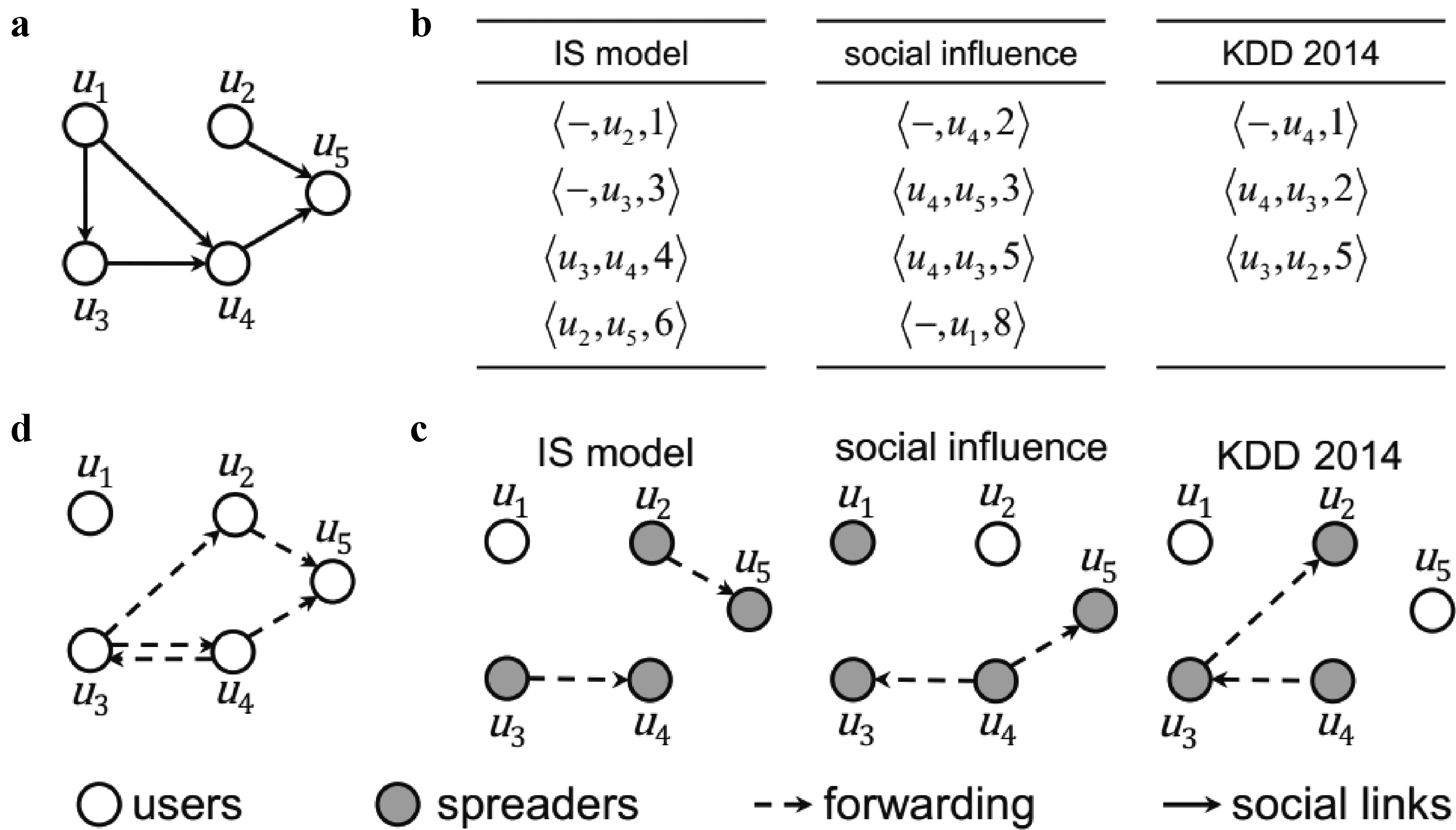
图 1 (a)社会网络;(b)三条消息的传播记录;(c)由(b)中所示传播记录所构建的三个传播网络;(d)根据所有传播记录综合构建的传播网络。
根据传播网络的定义,在传播网络中,一个用户的所有父亲节点都是该用户在某次信息传播中潜在的影响者。对此我们定义如下:
在一次信息传播中,用户v影响邻居集合内的所有节点都可能对用户v造成影响,并促成用户v对该信息进行转发。基于信息传播的一般假设[22]: 1)一个用户对一条信息有且仅能产生一次有效转发;2)当用户转发某信息时,其转发行为能够立即被网络中其他关联用户感知并造成影响;3)一个用户在一次信息传播中,有且仅能影响某一可能被其影响的用户一次。根据信息传播的一般假设,我们定义真实影响邻居集合如下:
定义2 真实影响邻居集合。关于信息m的一次信息传播,用户v的真实影响邻居集合
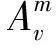
根据以上的符号及定义,本文采用离散选择模型(discrete choice model)[23]建模用户在转发信息m时所作的选择行为,其形式化如下:
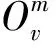
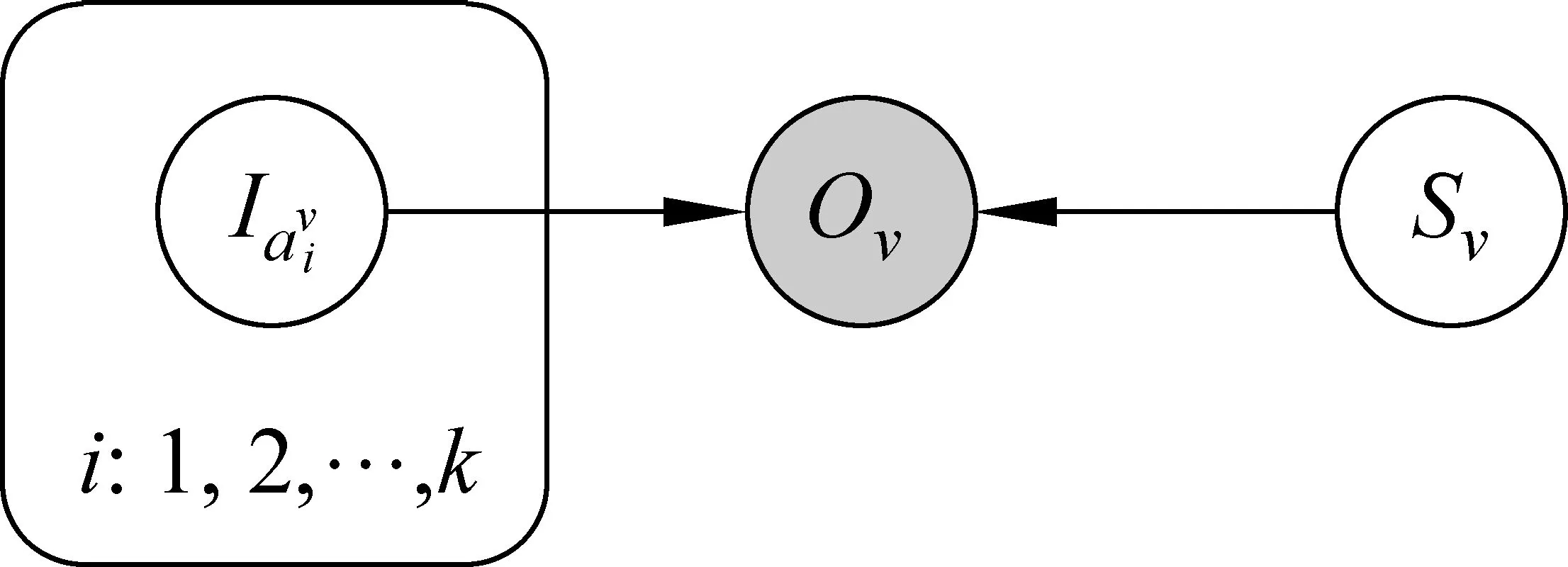
图2 FPM的概率图模型
假设用户间的转发选择过程相互独立,信息m传播中所有的转发选择过程可以建立其概率似然分布如下:
进一步地,假设各信息的传播独立。则在所有的信息传播C中,用户转发选择行为的概率似然分布可以表示为
求解目标是获得用户的属性矩阵I和S,使得等式在观测数据下获得最大似然。为了方便求解,本文将优化目标取负对数形式化为:
这里采用投影梯度法(Projected Gradient)[24]对公式进行求解优化。梯度的计算如下:

该算法的具体步骤在算法1中具体描述。

算法1 参数估计输入:给定时间内的传播记录,最大迭代步R输出:用户的影响力属性矩阵I和易感性属性矩阵S1.通过传播记录构建传播网络;2.随机初始化参数矩阵I,S;3.repeat4. fori=1tondo5. 计算∂L/∂Iu和∂L/∂Sv6. endfor7. 更新I和S8.until最大迭代步完成
4 实验结果及分析
本节将通过新浪微博数据对本文所提模型进行验证。首先,详细介绍所采用数据集的格式,抽取方法及训练、测试集的设定。接着引入两种评价方法对转发选择的预测结果进行评价,并讨论分析FPM模型中各参数对模型结果的影响。最后,选取几种较为典型的转发选择模型,通过与这些典型的转发选择模型比较,验证FPM模型的有效性。
4.1 数据集
实验数据集来自新浪微博,该数据集由WISE 2012 Challenge*http://www.wise2012.cs.ucy.ac.cy/challenge.html发布提供。数据集抓取了新浪微博从2009年9月17日至2012年2月17日的所有传播记录。本文选择其中2011年1月1日至2月15日的传播记录进行实验,将所抽取的数据按时间切分为三个等长的片段,分别记作数据集D1,D2,D3。去除了没有同时出现于三个切分片段数据上的用户及其对应传播记录,以保证在实验中所有用户的转发选择在一个闭集内。在实际传播过程中,存在用户仅在某信息下暴露一次就转发的实例。在这种情况下,真实影响邻居的集合大小为1,不需要对其进行转发选择行为的预测。因此本文的样本仅保留用户在某一信息下多次暴露的情况。实验采用交叉验证的方式共进行三组,所得的三个模型分别记作M1,M2,M3。交叉验证的策略如下: 第一轮R1在数据D1上训练获得模型M1,在数据D2和D3上进行测试;第二轮R2在数据D2上训练获得模型M2,在数据D1和D3上进行测试;第一轮R3在数据D3上训练获得模型M3,在数据D1和D2上进行测试;数据集的基本统计信息见表 2。
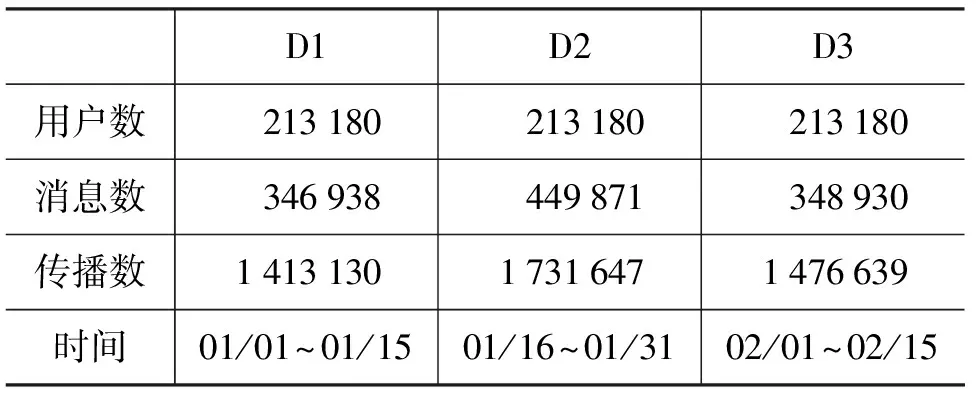
表 2 数据集的基本统计信息
4.2 评价标准
本文引入了两种评价标准用于判断模型对预测用户转发选择行为的准确度度量。
准确率: 准确率度量用于判断模型是否准确判断了用户的转发选择,计算其在总体预测样本上的准确率。其形式如下:
模型在准确率上的值越大,则模型的预测效果越好。
MRR (序值倒数的平均Mean Reciprocal Rank): MRR[25]是一种在信息检索领域中较为常见的统计测量方法,主要用于度量在排序中真实的首位元素在预测排序中的正确程度。MRR的具体定义如下:
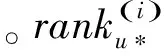
4.3 参数设置
为了能够让FPM模型取得较好的结果,本文设计了一系列实验对FPM模型参数进行调整。FPM所需要调整的主要参数包括了隐用户影响力与易感性属性维度和算法最大迭代步数。
隐用户影响力与易感性属性维度d: 用户的影响力与易感性属性维度d与FPM模型的表达能力直接相关,但是过高的维度同时会导致模型的过高的优化代价。因此需要对维度d的大小进行讨论,设置一个较为合适的维度值用于FPM模型。在实验过程中,本文取d=5,10,15,20,25,30,35,40,分别进行了测试。
图 3(a)展示了实验结果,由于训练数据分布于三个不同的传播时间区间,因此其传播表现存在一定的区分,这导致了所示曲线的差异。可以发现在三个模型关于维度d的调整中,均呈现维度与评价指标的正相关性,即维度越高FPM模型的预测性能在准确率和MRR两个度量指标上的结果更好。实验结果与本文的认识保持一致: FPM的表达能力提高能够明显改善模型的预测效果。考虑计算复杂度与效率的平衡问题,三个模型中同时取d=40。
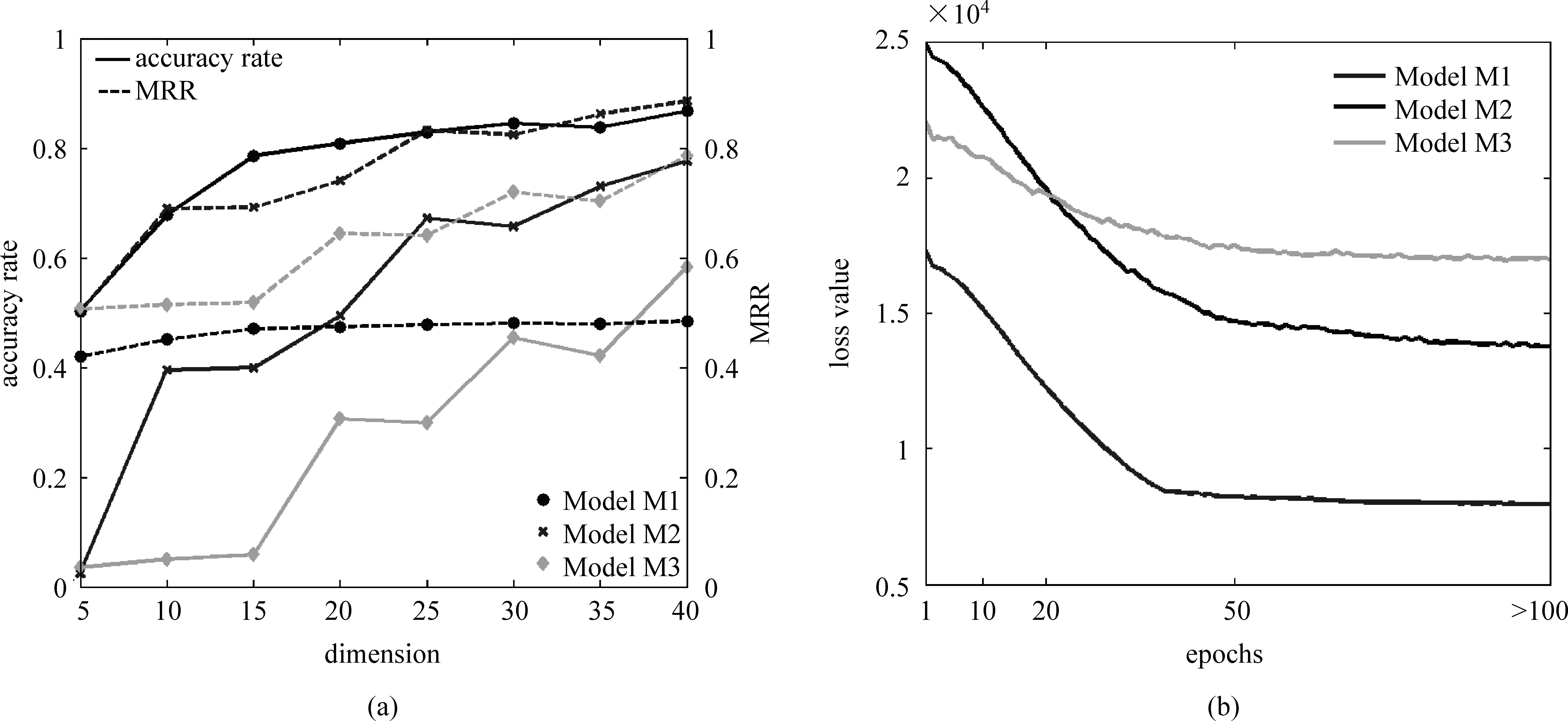
图3 FPM模型的参数设置
迭代步数R: 本文采用最大迭代步作为投影梯度法的收敛策略(其他的收敛策略见文献[24])。为了提高算法的运行效率,需要设置一个较为合理的最大迭代步。如图3(b)所示,三个模型在算法迭代到50次左右时都取得了较为良好的收敛效果。为了保证算法收敛,本文在三个模型中同时取最大迭代步R为100。
4.4 比较方法
为了评价FPM模型的有效性,本文引入了几种典型的转发选择模型进行比较:
1) 偏好模型(Preference Attachment Model,PAM)[6]。偏好模型是经典的网络生长模型,该模型认为网络中新加入的节点容易与节点度较高的节点产生链接。这里本文将其应用于信息传播中,假设用户容易与传播网络中节点度较高的节点发生转发行为。
2) 伯努利分布模型(Bernoulli Distribution Model,BDM)[26]。伯努利分布模型认为用户间的转发概率服从伯努利分布,该分布可以从历史传播记录中通过最大似然方法统计获得。用户的转发选择过程容易发生在具有较高转发概率的用户节点对之间。
3) 杰卡德系数模型(Jaccard Index Model,JIM)[26]。不同于伯努利模型,杰卡德系数模型认为用户间的转发概率服从杰卡德系数,该分布可以从历史传播记录中通过杰卡德系数的计算获得。用户的转发选择过程容易发生在具有较高转发概率的用户节点对之间。
4) 最大期望模型(EM Model,EMM)[27]。最大期望模型利用EM方法根据历史传播记录估计用户间的转发概率。用户的转发选择过程容易发生在具有较高转发概率的用户节点对之间。
5) 转发第一消息源策略(Forward First Strategy,FRS)。这种转发策略认为用户会从其真实影响邻居中转发最早发布该消息的用户。
6) 转发最末消息源策略(Forward Last Strategy,FLS)。这种转发策略认为用户会从其真实影响邻居中转发最近发布该消息的用户。
7) 任意转发策略(Forward Randomly Strategy,FRS)。这种转发策略认为用户会从其真实影响邻居中随机转发发布该消息用户。
4.5 比较结果
根据前述的实验方法,本文将FPM模型与选用的典型转发选择模型在真实数据集上进行比较,并通过两种评价指标进行了结果展示,实验结果列于表 4中。由于FRS,FLS,FRS策略仅考虑被转发用户,因此无法计算MRR值,表中对应部分空缺。从表中可以明显地发现,本文所提的FPM模型,在预测的准确率和MRR两项评价标准上均明显优于其他方法,特别是在准确率的度量上,显著高于次优的比较方法。这是因为FPM模型能够有效解决目前存在方法泛化能力不足的问题。将三个切分数据集所构成的传播网络进行对照发现,接近70%的网络连边在对照网络中没有出现,而典型的转发选择模型在处理这些情况时,其预测效果接近随机猜测。另外,FPM模型的结果同时也验证了对用户转发选择行为建模的有效性: 用户的转发选择行为主要取决于人际影响力,本文所提的FPM模型是对人际影响力的一种较为准确的建模方法。
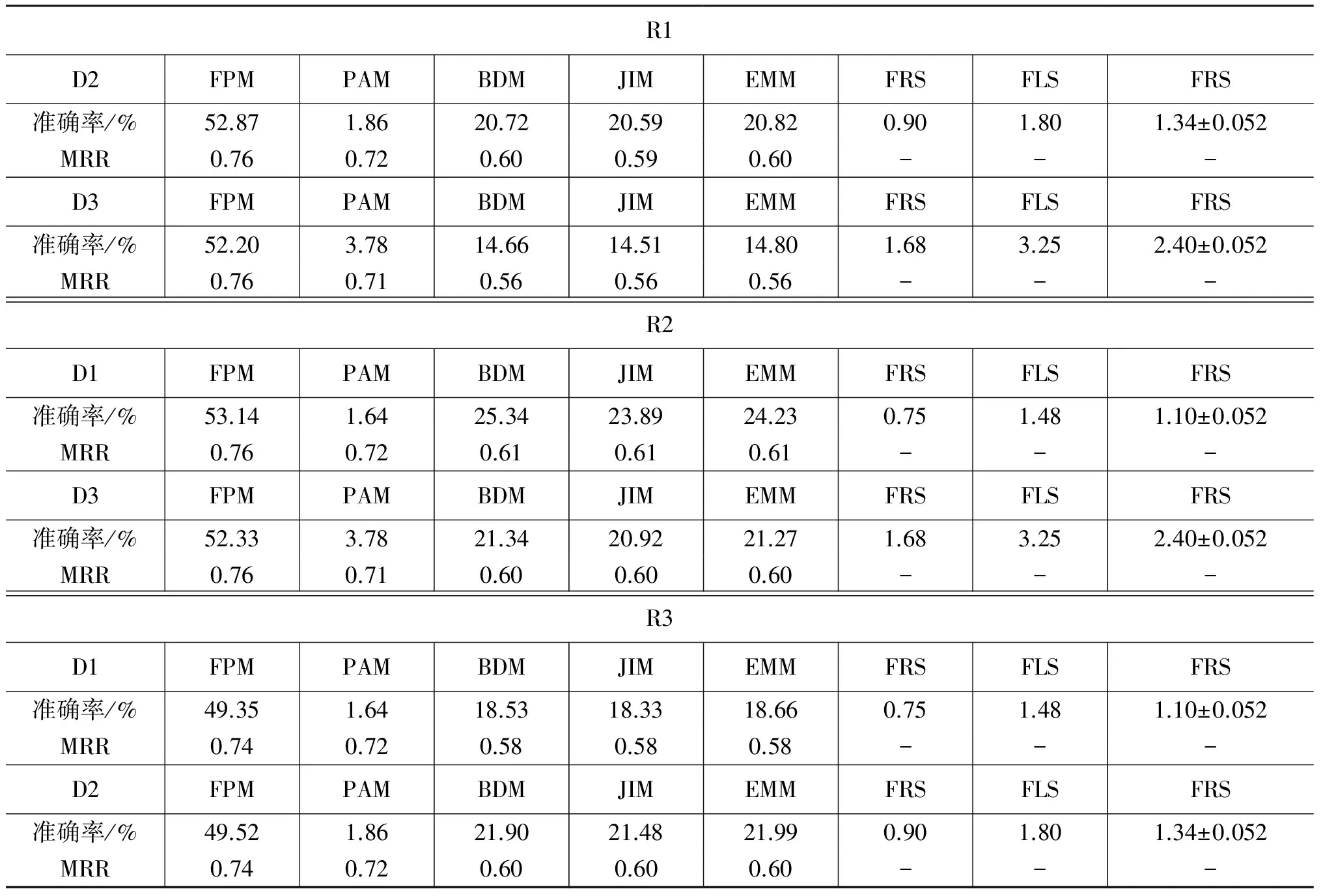
表4 PFM与比较方法在评价标准上的表现
5 结束语
本文提出了信息传播中所存在的用户转发选择问题,本文形式化了这一问题,并提出了一种用户转发选择模型,用于对用户的转发选择行为进行预测。本文认为用户的转发选择行为主要由人际影响力导致,这种人际影响力同时取决于信息发送者的影响力和信息接受者的易感性。本文建模了用户的隐影响力和易感性属性,提出了用户转发选择的FPM模型,并给出了高效的计算方式。该模型克服了目前存在工作中对转发选择行为的认识不足,模型泛化能力差和依赖用户传播属性获取的问题。通过在真实的新浪微博数据实验,我们对模型的运行参数和性能进行了调整和验证。通过与其他典型的转发选择模型比较,所提的FPM模型在准确率与MRR两项评价指标上均有显著提高。实验结果证明了FPM的有效性,本文所提的FPM模型是一种较为准确的对用户转发选择行为进行建模的方法。
[1] J Ugander, L Backstrom, C Marlow, et al. Structural diversity in social contagion[J]. Proceedings of the National Academy of Sciences, 2012, 109(16): 5962-5966.
[2] P Bao, H Shen, W Chen, et al. Cumulative effect in information diffusion: empirical study on a microblogging network[J]. PLoS ONE, 2013, 8(10): e76027.
[3] S Aral and D Walker. Identifying influential and susceptible members of social networks[J]. Science, 2012, 337 (6092): 337-341.
[4] J Leskovec, L A Adamic, and B A Huberman. The dynamics of viral marketing[J]. ACM Transactions on the Web (TWEB), 2007, 1(1): 5.
[5] J Huang, X Cheng, H Shen, et al. Exploring social influence via posterior effect of word-of-mouth recommendations[C]//Proceedings of the 5th ACM International Conference on Web Search and Data Mining. 2012: 573-582.
[6] A Barabási and R Albert. Emergence of scaling in random networks[J]. Science, 1999, 286 (5439): 509-512.
[7] P W Holland and S Leinhardt. Transitivity in structural models of small groups[J]. Comparative Group Studies, 1971.
[8] M Granovetter. The strength of weak ties[J]. American Journal of Sociology, 1973: 1360-1380.
[9] L C Freeman. A set of measures of centrality based on betweenness[J]. Sociometry, 1977: 35-41.
[10] L Katz. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43.
[11] P Bonacich. Power and centrality: A family of measures[J]. American Journal of Sociology, 1987: 1170-1182.
[12] J Tang, J Sun, C Wang, et al. Social influence analysis in large-scale networks[C]//Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2009: 807-816.
[13] M Gomez Rodriguez, J Leskovec, and B Schöl-kopf. Structure and dynamics of information pathways in online media[C]//Proceedings of the 6th ACM International Conference on Web Search and Data Mining. 2013: 23-32.
[14] S A Myers, C Zhu, and J Leskovec. Information diffusion and external influence in networks[C]//Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2012: 33-41.
[15] K Saito, K Ohara, Y Yamagishi, et al. Learning diffusion probability based on node attributes in social networks[C]//Foundations of Intelligent Systems. 2011: 153-162.
[16] P Cui, F Wang, S Liu, et al. Who should share what?: item-level social influence prediction for users and posts ranking[C]//Proceedings of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2011: 185-194.
[17] Y Wang, H Shen, S Liu, et al. Learning influence and susceptibility from information cascades[C]//Proceedings of the 29th AAAI Conference on Artificial Intelligence. 2015: 477-483.
[18] D M Romero, B Meeder, J Kleinberg. Differences in the mechanics of information diffusion across topics: idioms, political hashtags, and complex contagion on twitter[C]//Proceedings of the 20th international conference on World Wide Web. 2011: 695-704.
[19] D Gruhl, R Guha, D Liben-Nowell, et al. Information diffusion through blogspace[C]//Proceedings of the 13th International Conference on World Wide Web. 2004: 491-501.
[20] J Leskovec, M Mcglohon, C Faloutsos, et al. Patterns of cascading behavior in large blog graphs[C]//Proceedings of SIAM International Conference on Data Mining. 2007: 551-556.
[21] R Crane, D Sornette. Robust dynamic classes revealed by measuring the response function of a social system[J]. Proceedings of the National Academy of Sciences, 2008, 105(41): 15649-15653.
[22] D Kempe, J Kleinberg, É Tardos. Maximizing the spread of influence through a social network[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2003: 137-146.
[23] K Train. Qualitative choice analysis: Theory, econometrics, and an application to automobile demand[M]. MIT Press, 1986.
[24] C J Lin. Projected gradient methods for nonnegative matrix factorization[J]. Neural Computation, 2007, 19(10): 2756-2779.
[25] E M Voorhees. The TREC-8 Question Answering Track Report[C]//Proceeding of TREC. 1999: 77-82.
[26] A Goyal, F Bonchi, and L V Lakshmanan. Learning influence probabilities in social networks[C]//Proceedings of the 3rd ACM International Conference on Web Search and Data Mining. 2010: 241-250.
[27] K Saito, R Nakano, and M Kimura. Prediction of information diffusion probabilities for independent cascade model[C]//Knowledge-Based Intelligent Information and Engineering Systems. 2008: 67-75.
Predicting Forwarding Preference in Information Propagation
WANG Yongqing, SHEN Huawei, CHENG Xueqi
(CAS Key Laboratory of Network Data Science & Technology,Institute of Computing Technology, Chinese Academy of Sciences, Beijing 100190,China)
In information propagation, users have forwarding preference when receiving same message repeatedly. Modeling forwarding preference is fundamental to information propagation and other related applications, e.g., influence analytics, cascade dynamics and social recommendation. In this paper, we suggest forwarding preference is mainly affected by interpersonal influence, determined by both influence and susceptibility from the sender and the receiver, respectively. We propose to model such user-specific latent influence and susceptibility by the Forwarding Preference Model. We compare our proposed model with state-of-the-art forwarding preference models on the dataset from Weibo, which demonstrates that the proposed model consistently outperforms other methods at two evaluation measures.
information propagation; forwarding preference; influence; susceptibility

王永庆(1986—),博士研究生,主要研究领域为社交网络分析、数据挖掘。E⁃mail:wangyongqing@software.ict.ac.cn沈华伟(1982—),博士,副研究员,硕士生导师,主要研究领域为网络科学、社交网络分析、数据挖掘。E⁃mail:shenhuawei@ict.ac.cn程学旗(1971—),博士,研究员,博士生导师,主要研究领域为网络科学、网络与信息安全、互联网搜索与服务。E⁃mail:cxq@ict.ac.cn
1003-0077(2016)05-0057-08
2015-09-07 定稿日期: 2016-06-28
国家重点基础研究发展计划(“973”计划)(2014CB340401,2012CB316303);国家自然科学基金(61472400,61232010,61202215);北京市自然科学基金(4122077)
TP391
A

