超大跨混合钢桁梁斜拉桥静力非线性稳定分析

薛梦归，陈德伟，白植舟

（同济大学土木工程学院，上海 200092）

超大跨混合钢桁梁斜拉桥静力非线性稳定分析

薛梦归，陈德伟，白植舟

（同济大学土木工程学院，上海 200092）

为研究超大跨混合钢桁梁斜拉桥施工过程结构稳定性能，以贵州鸭池河特大桥（斜拉桥结构）为工程背景，分析了该桥施工过程中的静力非线性稳定性。采用ANSYS13.0有限元计算软件建立了全桥有限元模型，并模拟了该桥施工全过程。利用ANSYS特征值屈曲分析计算了施工过程中第一类线弹性稳定，用荷载增量迭代法计算了考虑双重非线性（几何和材料非线性）时的第二类稳定。最后得到两种计算的稳定安全系数、施工过程中稳定安全系数的变化趋势和每一施工阶段的失稳形态。分析计算结果，可以发现几何和材料非线性对结构静力稳定性影响非常明显。

超大跨斜拉桥；施工过程；线弹性稳定；非线性稳定；稳定安全系数

1 概述

近几十年来，斜拉桥以优美的造型和独特的结构性能被广泛应用。而且斜拉桥在向跨径更大、桥塔更高和拉索更长的方向发展，但与之对应的是整体刚度逐渐降低的趋势。特别是当斜拉桥主跨为钢桁梁时，施工过程中某些杆件的局部失稳将引起结构的整体失效。在以往的相关研究中[1-2]，更多的是以钢箱梁斜拉桥为主要研究对象，而对于边跨为预应力混凝土梁中跨为钢桁梁的超大跨径混合梁斜拉桥施工过程结构稳定性的研究不多。本文以鸭池河特大桥为工程背景，研究超大跨径混合钢桁梁斜拉桥施工过程中静力非线性稳定性，以确保结构的施工安全。

2 结构稳定计算理论

桥梁结构的稳定计算一般涉及到第一类稳定和第二类稳定。第一类稳定问题为分支点失稳，在线弹性范围内讨论。第二类稳定问题为极值点失稳，考虑几何非线性和材料非线性，有限元求解时为逐步加载的过程[3]。超大跨径斜拉桥属于柔性结构，具有大位移引起的几何非线性的特点，而且某些构件也可能进入塑性变形[4]。因此，精确的计算方法应考虑几何非线性和材料非线性。但第一类稳定问题理论上明确便于计算且为第二类稳定问题的加载上限，所以第一类稳定问题的求解也是必要的[3]。

2.1 第一类稳定计算理论

下面用有限元平衡方程来表达结构失稳的物理现象。结构的平衡方程为：

式中：K0为弹性刚度矩阵，Kσ为几何刚度矩阵，KL为大位移刚度矩阵，u为结构位移列阵，为结构荷载列阵。

第一类稳定在线弹性范围内的讨论，满足线性假设，处于初始构形线性平衡状态，所以KL应该为0，所以此时平衡方程为（K0+Kσ）u=R，在结构处于临界状态时，u变为u+Δu上式平衡方程仍满足，即（K0+Kσ）{u+Δu}=R，两式相减得到：

根据线性代数理论，当Δu有非零解时，必有|K0+ Kσ|=0。在小变形情况下Kσ与应力水平成正比，应力与外荷载也为线性关系，所以若某种参考荷载对应的结构几何刚度矩阵为，那么临界荷载下结构几何刚度矩阵为，临界荷载为，于是有，此式为第一类稳定问题的控制方程。稳定问题转化为求方程的最小特征值问题[9]。求得的最小特征值即为稳定安全系数，对应的特征向量即为失稳模态。

2.2 第二类稳定计算理论

结构的第二类稳定属于非线性极值问题，结构平衡方程仍为上式（1）。第二类稳定问题的求解思路是用考虑非线性的的有限元方法将荷载逐级加载，然后沿荷载—位移曲线进行追踪发现刚度矩阵奇异即的点，此时对应的荷载即为临界荷载Pcr，而与其结构荷载P的比值为结构稳定安全系数[5]。

式中：Ki-1为第i-1加载结束时的结构刚度矩阵，Δui为第i次加载时的结构位移增量，ΔRi为第i次荷载增量。

其中Ki-1可在第i次加载前求出，而ΔRi已知，则易求出第i次加载时的结构位移增量Δui。所以当第j级荷载增量作用结束时，结构承受的总荷载和总位移分别为：

式中：R0和u0分别为结构的初始荷载和初始位移。

所以通过上述的求解过程可以得到结构的荷载—位移曲线，最终得到结构第二类稳定的临界荷载Pcr和稳定安全系数。

3 工程应用及有限元模拟

3.1 工程简介

鸭池河特大桥主桥采用跨径布置为（2× 72+76+800+76+2×72）m的半飘浮双塔双索面混合钢桁梁斜拉桥，总体布置见图1，中跨为钢桁梁，边跨为预应力混凝土主梁。斜拉索索面采用半扇形布置，每个扇面由24对斜拉索组成，主跨钢混结合段设在主塔中心线处。

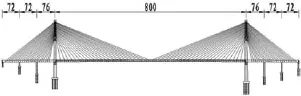
图1 大桥立面布置图

3.2 有限元模型

采用有限元软件ANSYS13.0建模计算。在有限元模型中主梁、主塔和桥墩用BEAM188梁单元模拟，拉索用link10杆单元，桥面板用梁格法简化建模。非线性分析中考虑大位移效应和P-效应；另外，材料非线性主要涉及到混凝土和钢材，参考我国混凝土结构规范，把混凝土材料的本构关系简化成分段线性化的折线模式[6]，钢材的本构关系为理想弹塑性模式。斜拉索钢材为硬钢，可假设为理想弹脆性材料，斜拉索一旦到达其极限状态，即视为拉断，将其从结构中拆除不再作为受力构件。有限元模型中考虑了施工过程的继承性和边界条件安装与拆除。ANSYS13.0建立的有限元结构分析模型如图2所示。

图2 鸭池河特大桥有限元模型

4 计算结果及分析

施工过程稳定计算分析中，考虑的主要荷载为结构自重。静力非线性稳定性分析中斜拉索索力加载到控制张拉力，结构自重进行逐步加载直到结构失稳。线弹性和非线性稳定安全系数，如下表1所示，稳定安全系数变化趋势如图3所示。

稳定安全系数 表1

图3 稳定安全系数变化趋势图

从图3可以看出施工过程中结构的线弹性稳定安全系数在5.72～37.10范围之内变化，满足我国斜拉桥规范中规定结构弹性稳定安全系数须大于4的要求。从分析结果来看，施工初期，结构稳定性呈逐渐增长趋势，在施工完成Z7节段之后，结构稳定性则呈逐渐降低趋势。经分析发现，Z0～Z7施工时结构的失稳模态为桥塔纵桥向失稳；而Z8～Z24施工时结构为桥塔横桥向和主梁扭转形成的耦合失稳，桥面铺装施工完时为桥塔纵向和主梁弯曲形成的耦合失稳。ANSYS13.0计算得到最大悬臂状态工况及施工完桥面铺装工况对应的失稳模态如图4(a)和(b)。

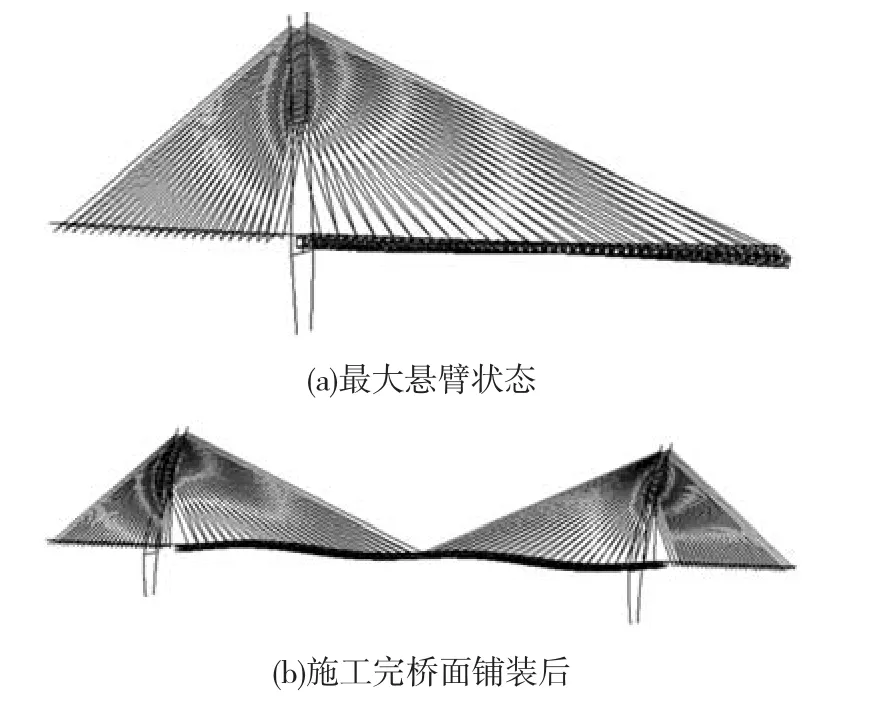
图4 典型阶段失稳模态

从图3可以看出考虑非线性时施工过程中的稳定安全系数在2.96～6.61范围之内变化，满足规范规定的“非线性稳定安全系数应大于2.0”的要求。从分析结果来看，Z0～Z4施工时结构稳定性呈较明显的下降趋势，Z5～Z23施工时结构稳定性呈缓慢下降趋势，合龙段Z24施工时结构稳定性增加。经分析发现，Z0～Z4施工时结构的失稳模态为桥塔纵桥向失稳；Z5～Z24施工时，加载至结构极限状态时结构失效均因斜拉索达到极限强度拉断所致。经过进一步分析发现，Z0～Z4施工时，在考虑非线性后加载至极限状态桥塔塔柱与下横梁交接处混凝土首先失效形成塑性铰导致整个结构失效；Z5～Z21施工时，加载至极限状态，边跨最外侧拉索先断裂，接着临近的拉索依次断裂，主跨拉索将桥塔拉向一侧失稳导致整个结构失效； Z22～Z24施工时，加载至极限状态中跨M21号拉索先断裂，接着临近的拉索依次断裂，中跨主梁竖向位移急剧增加导致整个结构失效。

ANSYS13.0计算得到施工Z0时桥塔塔顶处节点的荷载位移曲线如下图8（a），最大悬臂状态时主梁最末端节点荷载位移曲线如下图8(b)，其中K为加载倍数，UX为桥塔纵向位移，UZ为主梁竖向位移：

图8 典型阶段时节点荷载——位移曲线

从图3可以看出考虑双重非线性后，与线弹性稳定相比，稳定安全系数有很大的差别。在Z7节段时线弹性稳定安全系数是考虑双重非线性时的9.1倍。

5 结论及建议

结合ANSYS对该桥进行施工过程静力稳定性的数值分析，通过计算结果可以得到以下结论。

①该桥施工全过程弹性稳定安全系数均大于4.0，满足规范要求。

②该桥施工全过程非线性稳定安全系数均大于2.0，满足规范要求。

③考虑非线性时，稳定安全系数变化非常明显，且Z5及以后的节段施工加载至极限状态，结构失效均因斜拉索达到极限强度拉断所致。结构几何非线性对结构稳定性的影响远小于材料非线性的影响。

针对上述结论对该桥在施工过程中提出如下的建议：

①施工中应注意结构的非线性效应，结构非线性稳定安全系数比线弹性稳定安全系数要小得多，说明非线性因素对该桥的静力稳定性有很大的影响；

②重视不利工况的施工控制，在线弹性稳定安全系数计算中，到后期的施工阶段失稳均以主梁扭转为主，所以随着主跨悬臂长度的增加需采取一些有利于提高结构稳定性的必要措施，如尽可能减小悬臂端的临时施工荷载以及避免不对称的加载；

③重视斜拉索索力的控制，在考虑非线性的稳定安全系数计算中，Z5及以后的节段施工时加载至极限状态，结构失效均因斜拉索达到极限强度拉断所致，所以在每个施工阶段时需注意边跨最外侧拉索，及后期施工阶段时主跨M21拉索的索力监测和控制。

[1]赵雷，孙才志，杨兴旺.鄂东长江大桥施工过程非线性稳定性分析[J].西南交通大学学报，2012，42（5）：741-746.

[2]赵雷，李乔，张鸿，卜一之.苏通长江大桥结构非线性稳定性研究[J].土木工程学报，2013，46（1）：84-91.

[3]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2013：366-370.

[4]湖北省鄂东长江公路大桥工程建设指挥部.鄂东长江公路大桥工程[M].北京：人民交通出版社，2012：540-544.

[5]王勖成.有限单元法[M].北京：清华大学出版社，2012：652-654.

[6]GB50010-2010，混凝土结构设计规范[S].

[7]赵雷，张金平.大跨度拱桥施工阶段非线性稳定分析若干问题的探讨[J].铁道学报，1995，17（1）：76-84.

[8]杨兴旺.大跨度斜拉桥施工全过程非线性行为研究[D].成都：西南交通大学，2007.

[9]王新敏.ANSYS工程结构数值分析[M].北京：人民交通出版社，2007：451-465

[10]邓静.大跨度混凝土斜拉桥静力稳定性分析[D].成都：西南交通大学，2007.

U442

A

1007-7359（2016）06-0113-03

10.16330/j.cnki.1007-7359.2016.06.043

薛梦归（1993-），男，湖南益阳人，同济大学土木工程学院在读硕士，研究方向：评定与加固。