架空导线动态载流量的分析及改进算法
李天助, 汪 沨, 牛雪松, 易 畅
(湖南大学电气与信息工程学院, 湖南 长沙 410082)
架空导线动态载流量的分析及改进算法
李天助, 汪 沨, 牛雪松, 易 畅
(湖南大学电气与信息工程学院, 湖南 长沙 410082)
架空导线的输送容量在很大程度上受限于导线的温度,即架空导线存在一定的热稳定容量。本文基于IEEE Std 738和CIGRE架空导线载流量的计算方法,研究了导线热平衡方程中散热、发热的影响因素,分析关键因素对散、发热的影响程度。针对传统法将散、发热代入架空导线的稳态热平衡方程直接计算的动态载流量波动剧烈这一问题,提出在其基础上对一段时间的几个时刻所载电流单值加权求解架空导线动态载流量的改进算法。改进算法可极大地减小载流量的波动,导线温度的仿真分析表明导线温度在一个很小的范围内变化,增强了动态增容技术的实际应用性。
架空导线; 稳态热平衡方程; 暂态热平衡方程; 动态载流量
1 引言
目前架空线的额定载流量是为防止线路负荷增加时产生过热故障而制定的静态容量[1-3],架空输电线路的输送容量与环境温度、风速、风向、日照强度、导线的物理特性及导线所处的地理环境等因素有关[4]。静态容量是假定在极端恶劣的气象条件下(如日照强度大、风速低等)制定的,极端恶劣条件出现的概率很低,同时出现的概率则更低,据统计只有0.4%,可见输电线路存在极大的潜在输送能力[5,6]。
目前国内外主流的架空导线容量计算方法有国际电气和电子工程师协会(IEEE)标准“架空裸线的温度-电流计算”[7]、摩根(Morgan)公式、国际大电网会议(CIGRE)“架空导线的热特性”[8]及国际电工委员会(IEC)标准IEC1597-1995“绞合裸导线的架空电导线的计算方法”[9]。载流量都是在规定的导线最高允许温度下,通过导线的吸、散热平衡方程求得的[10,11],不同方法对平衡方程的各项计算略有不同,对相同导线在相同条件下计算得到的载流量有所差别[12]。通过导线的稳态热平衡方程直接求解得到导线的动态载流量波动太大,实际应用性不高[13-15]。
本文提出的方法将当前时刻前一段时间内的一组通过导线稳态热平衡方程直接求解得到的动态载流量数据的加权求和值作为当前时刻的载流量。经实际运行数据验证,该算法可以有效地减少动态载流量的波动性。通过导线暂态热平衡方程仿真分析导线温度,仿真结果表明只要选取适当的时间段长与权值,导线温度的变化可控制在一个非常小的范围内。
2 稳态及暂态热平衡方程
CIGRE计算方法的稳态及暂态热平衡方程分别为:
qc+qr+qw=qj+qM+qs+qi
(1)
(2)
式中,qc为对流散热(W);qr为热辐射散热(W);qw为蒸发散热(W);qj为焦耳热(W);qM为导线的磁滞损耗(W);qs为太阳辐射吸热(W);qi为电晕热(W);m为单位长度导线质量(kg);Cp为导线的比热容(J/(kg·℃));Tc为导线温度(℃)。
IEEEStd738-2006的导线热平衡方程中没有蒸发散热、磁力加热、电晕损耗。磁力加热是由于导体周围的环状磁通引起的涡流、磁滞、磁粘性,磁力加热只是在电流变化时才会存在,并且对于铝质导线在工频下是非常微弱的,可以忽略不计,但对于钢芯导线其效果就较为显著。虽然CIGRE的标准中包含了电晕发热与蒸发散热,但在实际计算载流量时并没有计算电晕散热与蒸发散热,因为电晕只会在导体表面电场强度很高的情况下发生,而且仅当架空导线被雨淋湿了才会有蒸发现象。
3 导线的发热
架空导线通过大电流时,导线产生焦耳热,对于交流电会存在集肤效应,对于钢芯绞线还会产生磁滞损耗,若导线表面电场强度过大还有可能存在电晕损耗。架空导线直接暴露在太阳辐射下,导线会吸收太阳辐射。
3.1 电流作用
为方便计算欧姆热、集肤效应及温度引起的电阻改变,CIGRE标准中采用式(3)的焦耳热集中表示电流作用热:
qj=kjI2Rdc[1+α(Tav-20)]
(3)
式中,kj表示直流电阻到交流电阻的转换系数;Rdc为20℃时架空线的直流电阻;α为导体电阻的温升系数;Tav为导线的平均温度。
IEEE 标准也是引入一个与温度线性相关的电阻的焦耳热来集中表示电流作用热。
3.2 太阳辐射作用
太阳辐射对单位长度导线的加热功率与太阳辐射强度、导线横截面积、导线对太阳辐射的吸收系数及太阳光线与导体轴线夹角等因素有关。如已知太阳辐射强度,各种方法、标准对导线的太阳辐射吸热功率都采用式(4)计算:
qs=QsAε
(4)
式中,Qs为太阳辐射强度(W/m2);A为单位长度导线横向投影面积(m2);ε为导线对太阳辐射的吸收系数。
实际应用中,不易准确获取太阳辐射强度,太阳辐射计需要定期维护,因此,IEEE Std 738-2006与CIGRE都给出了太阳辐射强度关于纬度、天数、空气质量、海拔高度的计算法则[7,8]。
4 导线的散热
导线的散热形式有对流散热、热辐射散热,在淋湿的情况下还存在蒸发散热。
4.1 对流散热
对流散热是导线散热的主要形式(占散热总量的80%左右),对流散热与导线对空气的温差、导线尺寸、风速、风向等因素有关,IEEE与CIGRE对导线的对流散热计算有所差别。
IEEE Std 738-2006将对流散热分为强风对流、弱风对流及自然对流来计算,最后取三者中的最大值作为架空导线的对流散热。
CIGRE在计算对流散热时还考虑了导线表面粗糙度的影响,为方便计算引入了努赛尔数、雷诺系数、格拉晓夫数、普朗特数等中间变量。强迫对流散热公式为:
qc=πkf(Tc-Ta)NuKangle
(5)
式中,Tc为导线温度(℃);Ta为环境温度(℃)。
空气热导率
kf=2.42×10-2+7.2×10-5Tfilm
(6)
努赛尔数
Nu=B1(Re)n
(7)
雷诺数
(8)
相对空气密度
ρr=exp(-1.16×10-4He)
(9)
风向因子
(10)
其中,B1、n为与雷诺数Re及表面粗糙度Rf有关的常数,具体取值如表1所示;Φ为风向与导线轴向的夹角(°);Tfilm为空气温度(℃);He为海拔高度(m)。
(11)
式中,D为d位导线最外层绞线直径(m)。

表1 常数B1、n的取值Tab.1 Value of constant B1,n
自然对流时的对流散热式为:
Nu=A2(Gr·Pr)m2
(12)
式中

(13)

(14)
A2、m2为常数,取值见表2。

表2 常数A2、m2的取值Tab.2 Value of constant A2, m2
当风速较小(小于0.5m/s)、风向难以确定时,对流散热取下面三者中的最大值。
(1) 风向角取45°,按强迫对流计算;
(2) 风向因子取0.55,按强迫对流计算;
(3) 按自然对流计算。
虽然IEEE Std 738-2006与CIGRE的风向因子表达形式差别较大,但两种方法的风向因子值非常接近。
以导线直径0.03m、导线允许温度70℃、环境温度25℃、海拔0m、风向45°的条件为例,比较IEEE与CIGRE对流散热的计算,单位长度导线对流散热与风速的关系计算结果如图1所示。

图1 对流散热与风速的关系Fig.1 Relation of convection cooling with wind speed
由图1可看出:①在风速较低(小于2m/s)及粗糙度小于0.05时IEEE与CIGRE的计算值几乎相同;②当风速较大时,由于CIGRE考虑了导线粗糙度的影响,对流散热明显比IEEE的计算值要大,且随风速的增大有增大的趋势。
4.2 热辐射散热
导线的热辐射散热各种方法、标准所采用的计算公式相同,如式(15)所示:
qr=πDδσB[(Ts+273)4-(Ta+273)4]
(15)
式中,D为导线直径;δ为导线的辐射系数,一般取值与ε相同;σB为波尔兹曼常数5.6697×10-8(W/(m2·K));Ts为导线表面温度。
绝大多数的架空导线在多数的风速条件(1~5m/s)、强日照条件(500~1000W/m2)、环境温度(0~40 ℃)下各项在总发散热中的比例见表3。

表3 各项在导线总发散热中的比例Tab.3 Proportion of various heat dissipation of wire
5 动态容量的计算
5.1 传统法动态载流量的计算
导线处气象传感器通过短距离无线通信将实时测量的风速、风向、日照强度、环境温度信息发送给安装在杆塔上的GPRS模块,GPRS模块每隔一定的时间就发送一组气象数据。终端上微机收到一组气象数据后,结合上位机配置的导线允许温度、导线直径、电阻率、表面吸热系数等不变的特性参数,根据计算标准(本论文采用CIGRE)依次计算出日照吸热、热辐射散热、对流散热,直接代入稳态平衡方程求焦耳热,进而求解出导线当前时刻的最大载流量。
表4为我国南方电网某安装了气象传感器的架空导线1h的气象数据。
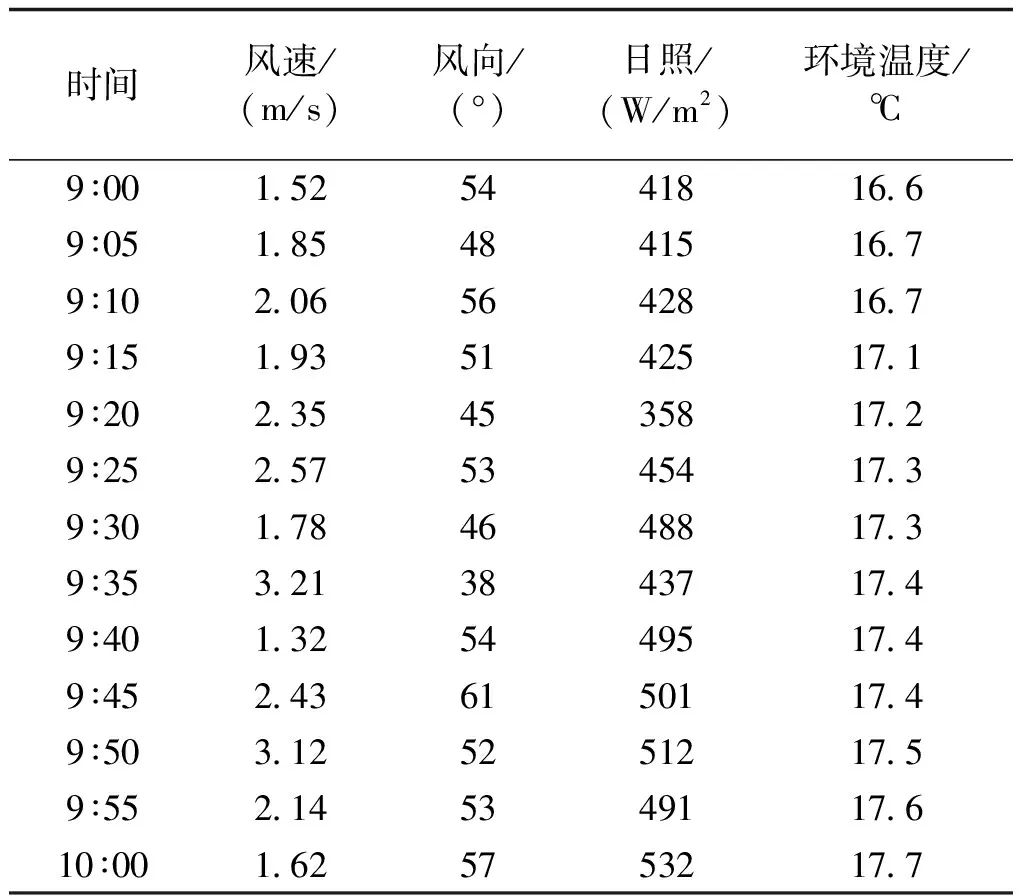
表4 气象数据Tab.4 Meteorological data
5.2 传统法的缺点
由表4可知,环境温度变化非常缓慢,日照强度的变化也比较缓慢,但影响载流量最大的风向、风速变化却很快,这就使得直接经导线稳态热平衡方程计算的载流量存在剧烈的波动。而电力调度是一项统筹兼顾、十分复杂的工作,因此,采用传统法计算导线动态载流量的实际应用性不够强。
5.3 改进算法
为了改善动态载流量的波动性,提出了如式(16)所示的载流量的计算法:
(16)

5.4 权值的确定
按月份近似均匀分布地选取了15天的历史气象数据,对选取15天中第k天的所有组气象数据采用传统法计算其载流量Ii,k-1,然后求出相隔j个时间间隔载流量的相关系数,既Ii,k-1与Ii+j,k-1的相关系数βj,k-1。图2为Ii,0与Ii+1,0的散点图,其相关系数为0.8079225。

图2 Ii,0与Ii+1,0的散点图Fig.2 Scatter graph for Ii,0 and Ii+1,0
令所有的β0,k=1
(17)
对我国南方电网安装了气象传感器12h的数据分别采用传统法、加权求和值法(m取6、11,即30min、60min)计算动态载流量,结果如图3所示。

图3 动态载流量的比较Fig.3 Comparison of dynamic current carrying capacity
由图3可以看出,在传统法的基础上加权求和明显比传统法计算的动态载流量曲线要平缓得多,60min加权比30min加权曲线更为平缓,但30min加权的效果也相当明显。
5.5 导线温度的仿真分析
由于图3所示的载流量并不是导线实际的载流量,导线的温度只能通过仿真分析。风速、风向和日照等气象条件都一直在变化,本文假定传感器所测相邻的两个数据间隔内气象条件保持不变。若架空导线通过图3所示的电流,导线的发热不等于散热,导线的温度可由暂态热平衡方程来求得。导线温度仿真计算流程图如图4所示。

图4 导线温度仿真计算流程图Fig.4 Flowchart of conductor temperature simulation
采用图3的数据,分别利用30min加权求和值与60min加权求和值计算导线的温度变化曲线,结果如图5所示。

图5 导线温度的变化曲线Fig.5 Wire temperature curve
可以看出,若通60min加权电流导线温度变化范围较大,其最大值超过导线允许温度(70℃)8℃左右,而采用30min平均值法导线温度变化范围较小,最大值高于导线允许温度一个很小的值(3℃以内),而这对线路的安全可靠运行并无影响[16]。由以上分析可知,30min加权所得载流量能很好地满足载流量平缓及导线最高温度不超限的要求。
6 结论
对流散热是架空导线散热的主要形式,因而风速对载流量的影响最大。因CIGRE相比于IEEE考虑了架空导线的粗糙度,CIGRE计算得到的架空导线载流量明显比IEEE的计算值要大。架空导线中存在极大的隐性容量,在绝大多数情况若采用动态增容技术可增容10%~30%左右。在计算动态载流量时,允许导线温度有一个极小的波动范围,对一段时间载流量采用本文提出的加权求和法计算得到的动态载流量并不会随气象条件的波动而猛烈波动,这极大地增大了其在电力调度时的参考性,增强了动态增容技术的实际应用性。
[1] 张启平,钱之银(Zhang Qiping, Qian Zhiyin).输电线路实时动态增容的可行性研究(Study on real-time dynamic capacity-increase of transmission line) [J].电网技术(Power System Technology),2005,29(19):48-51.
[2] 谭卫成(Tan Weicheng).基于最优化模型的深圳电网高压交流输电线路增容方案研究(HVAC transmission line capacity enhancing scheme based on optimization model in Shenzhen power grid)[D].广州:华南理工大学(Guangzhou: South China University of Technology),2012.
[3] 刘刚,阮班义,张鸣(Liu Gang, Ruan Banyi, Zhang Ming).架空导线动态增容的热路法暂态模型(A transient model for overhead transmission line dynamic rating based on thermal circuit method)[J].电力系统自动化(Automation of Electric Power Systems),2012,32(16):58-62.
[4] 任丽佳,盛戈暤,曾奕,等(Ren Lijia, Sheng Gehao, Zeng Yi, et al.).动态提高输电线路输送容量技术的导线温度模型(A conductor temperature model based on dynamic line rating technology)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(5):40-44.
[5] Dimitrios Vlachos, Patroklos Georgiadis. A system dynamics model for dynamic capacity planning of remanufacturing in closed-loop supply chains [J]. Computers & Operations Research, 2007, 34(2):367-394.
[6] 柯广,易灵芝,周诗霞,等(Ke Guang, Yi Lingzhi, Zhou Shixia, et al.).基于双回路交直流同线输电方式的线路增容研究(Study of capacity-increase for simultaneous AC-DC transmission based on double circuit AC transmission line)[J].电力系统保护与控制(Power System Protection and Control),2013,41(6):26-31.
[7] IEEE Std 738TM-2006. IEEE standard for calculating the current-temperature of bare overhead conductors[S].
[8] CIGRE. The thermal behavior of overhead conductors[J]. Electra, 1992, (10):107-125.
[9] IEC1597-1995. Overhead electrical conductors - Calculation methods for stranded bare conductors[S].
[10] I Albizu, E Fernandez, A J Mazon, et al. Influence of the conductor temperature error on the overhead line ampacity monitoring systems[J]. IET Generation Transmission & Distribution, 2011,5(4):440-447.
[11] I Albizu, A J Mazon, I Zamora. Methods for increasing the rating of overhead lines[A]. 2005 IEEE Russia Power Tech [C]. 2005. 1-6.
[12] L Staszewski, W Rebizant. The differences between IEEE and CIGRE heat balance concepts for line ampacity considerations[A]. Modern Electric Power Systems[C]. 2010.1-4.
[13] 王孔森,盛戈暤,王葵,等(Wang Kongsen, Sheng Gehao, Wang Kui, et al.).输电线路动态增容运行风险评估(Operation risk assessment of a transmission line dynamic line rating system)[J].电力系统自动化(Automation of Electric Power Systems),2011,35(23):11-15.
[14] 赵文彬,李彗星(Zhao Wenbin, Li Huixing).基于智能电网需求的输电线路状态监测系统建设(Construction of transmission line state detection system based on smart gird requirements)[J].华东电力(East China Electric Power),2010,38(8):1212-1216.
[15] 刘刚,雷成华,刘毅刚(Liu Gang, Lei Chenghua, Liu Yigan).根据电缆表面温度推算导体温度的热路简化模型暂态误差分析(Experimental analysis on increasing temporary capacity of single-core cable)[J].电网技术(Power System Technology),2011,37(5):212-217.
[16] 张启平,钱之银(Zhang Qiping, Qian Zhiyin).输电线路增容技术(Capacity of transmission line)[M].北京:中国电力出版社(Beijing: China Electric Power Press),2010.
Analysis and improved method for overhead conductor dynamic ampacity
LI Tian-zhu, WANG Feng, NIU Xue-song, YI Chang
(College of Electrical Information Engineering, Hunan University, Changsha 410082, China)
The ampacity of the overhead transmission line is largely limited by the temperature of conductors since there is a fixed range of overhead conductors ampacity of thermal stability. Based on IEEE Std 738 and CIGRE’s method for calculating overhead conductor ampacity, this paper discussed related factors which have impact on the cooling and heating dynamic process of heat balance equation. Key factor’s impact on ampacity was analyzed. For the issue of highly oscillatory of dynamic ampacity brought by the utilization of traditional method which directly substitute cooling and heating terms into the steady heat balance equation, this paper suggests a solution which uses weighted current value at several points in a period of time to solve conductors’ dynamic ampacity based on the traditional method. This method can largely reduce the oscillatory of dynamic ampacity and the temperature of conductors varies in a tiny interval based on simulation analysis, which enhance practical application of dynamic capacity-increase technology.
overhead conductor; steady-state heat balance equation; transient heat balance equation; dynamic ampacity
2013-06-19
李天助(1988-), 男, 湖南籍, 硕士研究生, 研究方向为架空导线动态增容技术; 汪 沨(1972-), 男, 满族, 辽宁籍, 教授, 博导, 主要研究方向为高电压绝缘技术。
TM726
A
1003-3076(2016)11-0059-06

