分布式电驱动车辆回馈制动控制策略研究

伍令飞, 王丽芳, 苟晋芳, 张俊智

(1. 中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所， 北京 100190； 2. 中国科学院大学， 北京 100049； 3. 汽车安全与节能国家重点实验室， 清华大学， 北京 100084)

分布式电驱动车辆回馈制动控制策略研究

伍令飞1,2, 王丽芳1, 苟晋芳1, 张俊智3

(1. 中国科学院电力电子与电气驱动重点实验室， 中国科学院电工研究所， 北京 100190； 2. 中国科学院大学， 北京 100049； 3. 汽车安全与节能国家重点实验室， 清华大学， 北京 100084)

回馈制动能有效提高分布式电驱动车辆的能量效率。论文分析了分布式电驱动车辆回馈制动系统的结构、电机的性能及制动法规的约束条件，提出了基于非线性规划方法的最大能量回馈制动控制策略，并结合回馈制动系统的特性分析了制动力分配的特点。通过仿真分析了典型制动过程及典型工况循环的制动能量回收效果，结果表明，与理想制动力分配策略相比，本文提出的回馈制动控制策略能获得更高的能量回收效率。

回馈制动； 分布式电驱动车辆； 制动力分配； 能量回收效率

1 引言

回馈制动是有效提高电动汽车能量效率的重要途径，首先在单轴驱动的电动汽车上得到应用，通过电机回馈力矩参与制动对车辆动能进行回收以提高能量效率。回馈制动典型的控制策略包括基于理想制动力分配的串联控制策略和并行制动力分配策略等[1,2]。

分布式电驱动汽车具有四轮驱动力、制动力独立控制的特点，可实现灵活的驱制动控制。由于各车轮均可采用电机进行回馈制动，其能量回收效果优于单轴驱动的电动汽车。目前对分布式电驱动车辆的回馈制动控制策略的研究主要集中在串联式的回馈制动控制策略。郑宏宇等人提出将理想制动力分配等策略应用于分布式电驱动车辆[3]，但理想制动力分配方案不能实现最大化回收制动能量；W Xu等人采用基于电机效率map图对制动力进行分配的方法，使得电机能最大回收能量[4]，但没有考虑回馈制动系统的性能及制动法规的约束，存在影响制动稳定性的隐患；P Andrew等人提出了纯电制动的分布式电驱动车辆制动控制方法[5]，在车辆满足制动法规要求的基础上优化能量回收效率，但纯电制动的强度受限于电机的功率，无法满足大强度制动需求，还需要考虑电机和液压制动系统联合制动的情况。

因此，本文对电机-液压复合制动系统的性能进行综合分析，在满足制动法规要求的前提下，制定回馈制动控制策略，寻求前轴制动力和后轴制动力、液压制动力和电机制动力的合理分配方案，使车辆在保证制动稳定性的基础上回收尽可能多的能量。

2 仿真模型

本文所讨论的分布式电驱动车辆为微型电动汽车，采用四个永磁直流电机通过变速器独立驱动四个车轮。由于纯电制动无法满足车辆所有工况下的制动需求，因此车辆配备了液压制动系统，车辆的整体参数如表1所示。

表1 分布式电驱动车辆性能参数Tab.1 Parameters of distributed drive electric vehicle

2.1 车辆动力学模型

车辆在水平路面直线行驶并处于正常的驱制动状态时，轮胎处于线性工作区间，此时车身的受力与运动状态可表示为：

(1)

式中，u为车速；F0为车辆的驱动力或制动力；m为车辆质量；g为重力减速度；f为滚动阻力系数；CD为风阻系数；ρ为空气密度；A为迎风面积；i0为传动比；r为车轮滚动半径；Tmi和Thi分别表示作用于各车轮的电机转矩和液压制动力矩，取驱动车轮的方向为正，i=1～4分别表示左前轮、右前轮、左后轮、右后轮。

2.2 电池模型

车辆采用锂离子动力电池组作为动力源，可以通过电机驱动车辆和电机发电回收车辆的制动能量。电池的额定电压为180V，容量为55Ah。电池的特性可采用等效电流模型进行描述，如图1所示[6]。其中Em和R0为开环电压和内阻，R1、C1和R2、C2用于描述电池的动态特性，以上特性参数均随电池SOC变化，可通过电池试验拟合得出。电池的功率P0、电压U0和电流I0可采用式(2)描述：

(2)

电池的SOC变化可采用式(3)描述：

(3)

式中，SOCinit表示电池的初始SOC；CN表示电池的等效电容。

图1 等效电流模型Fig.1 Equivalent circuit model of battery

2.3 电机模型

由于电机物理模型较为复杂，而回馈制动控制策略仅关注于给定的电机特性下，制动系统的制动力分配对制动能量回收效果的影响，故采用了效率图模型描述再生制动状态下电机经过发电及DC-DC变换将机械能转化为电池电能的效率。电机再生制动效率图参考了某车用电机的实测数据，如图2所示。根据电机的转速和转矩可得到电机的效率。回馈制动过程中电机传递到电池的能量Pmi为：

(4)

式中，ωmi为电机的转速，ωmi=i0u/r；η(Tmi,ωmi)为当前状态下电机的再生制动效率。

图 2 电机再生制动效率图Fig.2 Efficiency of motor under regenerative braking

电机的转矩相比车轮的动力学响应要快得多，故电机转矩的动态响应可简化为二阶系统[7]，即

(5)

2.4 液压制动系统模型

由于回馈制动没法完全满足车辆制动性能，需要配备常规的液压制动系统。本文所讨论的液压制动系统由制动踏板、制动主缸、高速开关阀及制动轮缸等组成。

驾驶员通过制动踏板开度控制制动主缸压力，为保证制动的安全，制动踏板需要保留一定的自由行程，主缸的压力与制动踏板的关系为：

(6)

式中，Pm为主缸的压力；α为制动踏板开度。

制动轮缸通过高速开关阀与制动主缸及低压蓄能器连接，结构如图3所示。控制器通过控制高速开关阀的动作对制动轮缸进行增压或减压控制，开关阀采用PWM控制方式。基于高速开关阀的压力流量特性[8]，轮缸压力的控制可描述为：

(7)

式中，Pm、Pw、P0分别为制动主缸、制动轮缸及低压蓄能器的压力；Cd为流通系数；Avi、Avd分别为进油阀和出油阀的流通面积；k为制动液的体积弹性惯量；φvi、φvd分别为进油阀和出油阀的压力流量系数；V0为制动轮缸的储液体积；τ1、τ2分别为进油阀和出油阀的PWM控制信号。

图3 液压制动系统结构图Fig.3 Structure of hydraulic brake system

制动轮缸压力作用于制动盘或制动鼓等制动器，产生作用于车轮的摩擦制动力矩，其表达式为：

(8)

式中，Pwi为各轮缸的压力；f1、f2为前后轴制动器的摩擦系数；A1、A2为前后轮缸的有效制动面积；r1、r2为前后轴制动器有效制动半径。定义β为前后制动器制动系数之比，β=f1A1r1/(f2A2r2)。

3 回馈制动控制策略

当车辆处于制动工况时，需要根据车辆状态选择不同的制动模式。图4描述了车辆制动模式控制过程。车辆处于制动工况时，需要根据车辆的状态信息选择制动模式。当检测到轮胎出现抱死时，需要触发防抱死控制。若未触发防抱死控制，则根据车辆的相关状态信息判断选择是否进行回馈制动。当出现以下情况时，采用常规液压制动：①电池SOC高于门限值95%时，无法回收能量；②车辆制动减速度大于门限值6m/s2时，认为车辆处于紧急制动，采用常规液压制动以保证安全；③电机转速低于600r/min时，回馈制动力矩不稳定，采用常规液压制动以保持车辆的制动稳定性。

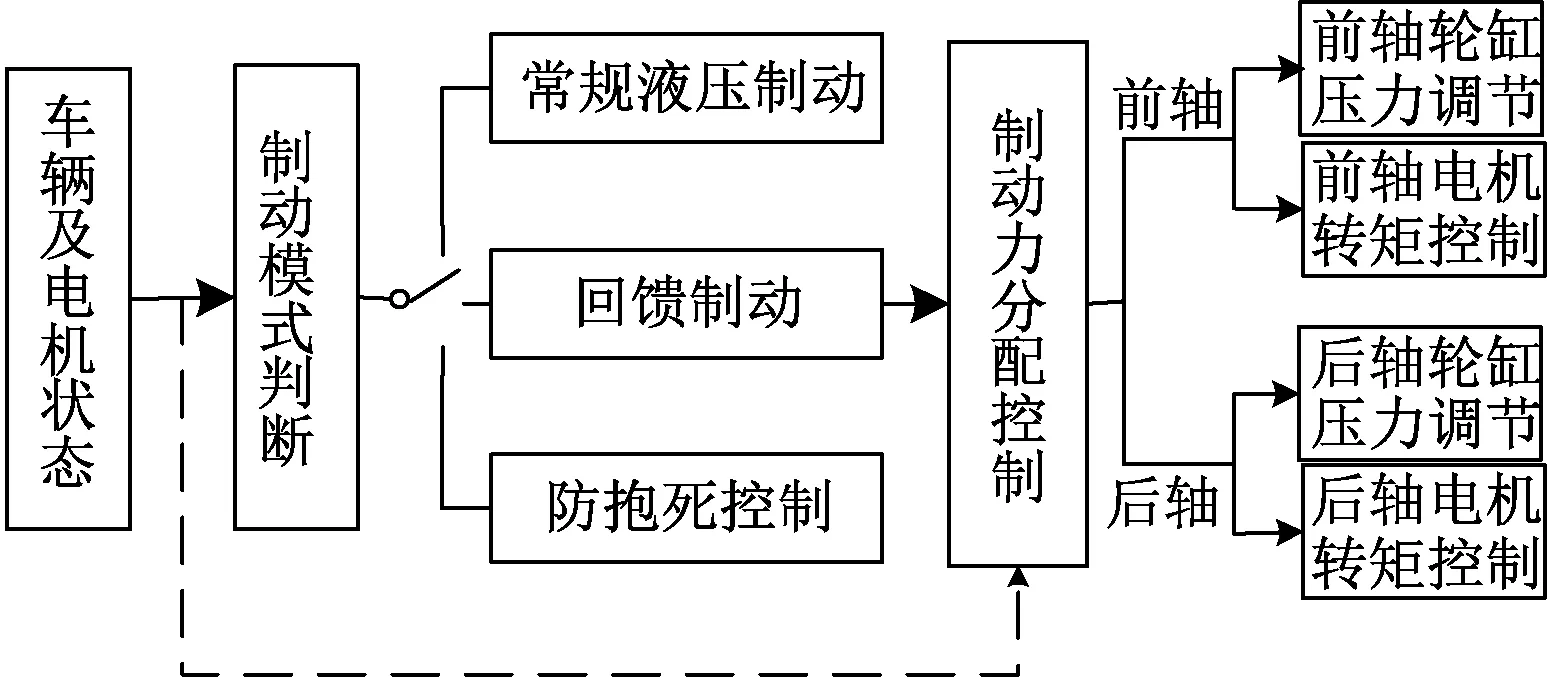
图 4 车辆制动控制结构Fig.4 Structure of vehicle braking control

车辆回馈制动过程的能量流动如图5所示。小部分的车辆动能消耗于克服风阻和滚阻做功，大部分由制动系统吸收。液压制动系统无法对制动能量进行回收，电机则通过发电将车辆动能转化成电能传递到动力电池组，能量传递过程中存在能耗损失。定义制动能量回收效率为：

(9)

式中，Ereg为制动过程回收到电池的能量；Ebrk为制动过程中可能进行回收的能量，即液压制动和电机制动所消耗的能量。

图5 回馈制动过程能量流动图Fig.5 Energy flow of regenerative braking

回馈制动控制策略的目的是通过协调作用于前后车轮的液压制动力和电机制动力，提高制动能量回收效率，回收尽可能多的能量。

为保证驾驶员的驾驶感觉，本文采用协调式的回馈制动控制策略。与常规液压制动方式相比，采用回馈制动后总的制动力矩Tbrk保持不变，即

(10)

定义制动力分配系数Ω为前轴制动力占总制动力的比例，即

(11)

为保持车辆的直线行驶，对制动力矩进行分配时需要避免横摆力矩，前后轴上左右侧的制动力矩保持相同。而为了最大回收制动能量，对液压制动与电机回馈制动进行分配时应当优先采用电机回馈制动，轴上的制动力分配满足以下条件：

(12)

式中，Tm_lim表示当前电机的最大制动力矩。

制动力分配系数一定时，可确定各电机的工作状态，则有效回收的功率为：

(13)

前后轴制动力分配受到制动系统结构及相关制动法规的约束。前后轴的最大制动力受到液压制动系统结构及电机回馈制动能力的约束，即

(14)

在制动过程中，为保证车辆的制动安全，前后轴附着利用系数需要满足制动法规的要求。前后轴附着利用系数ψf、ψr的定义为：

(15)

式中，Fbf和Fbr为作用于前后轴的制动力；Fzf和Fzr为车辆前后轴的载荷；z为车辆的制动强度；a和b为车辆质心到前后轴的距离；L为车辆的轴距；h为车辆的质心高度。

当前轴和后轴的附着利用系数相同时，车辆处于理想制动力分配状态。

根据ECE制动法规的要求，在不同的制动强度下前后轴的附着利用系数应当满足以下要求：

(16)

整理可得制动法规对回馈制动过程制动力分配的约束条件为：

在任意的制动工况下，制动力需求一定，通过合理选择制动力分配系数，可使得制动回收功率最大。故特定工况下的最大制动能量回收可描述为非线性规划问题。制动力分配系数的控制可描述为：

(18)

最优解可通过非线性规划的离线求解求得，根据约束条件计算出制动力分配系数的可行域，再计算整个可行域内不同制动力分配系数下的回收功率，取回收功率最大的点作为最优解。若存在多个点回收功率相同，则选取最接近理想制动力分配系数的点作为最优解。通过离线计算可得出不同工况下的制动分配系数表，如图6所示。车辆制动过程中无需实时计算，根据车辆状态信息，通过查表即可得到制动力分配方案，实时性较强。

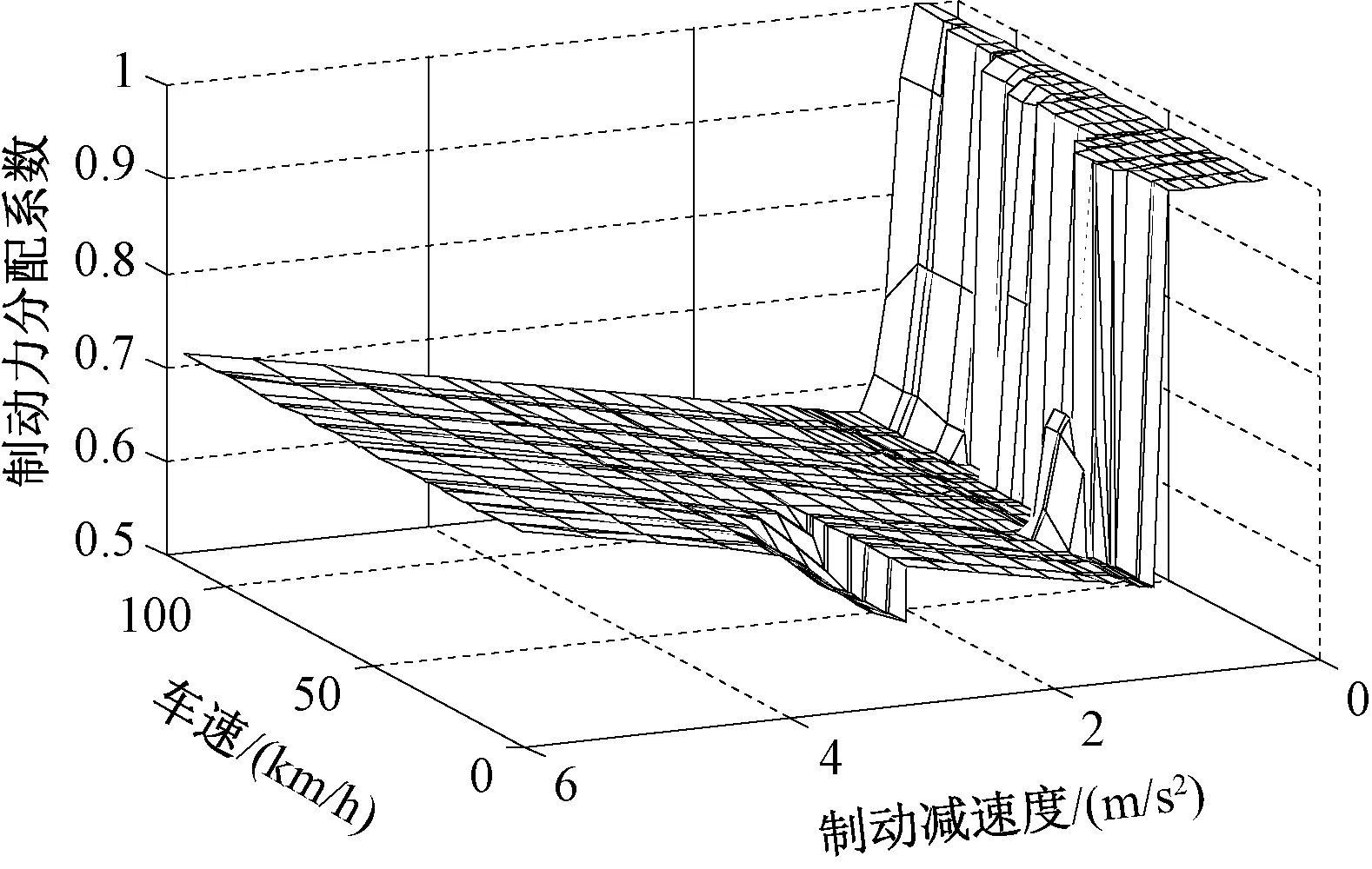
图 6 制动力分配方案Fig.6 Solution of braking force distribution

由图6可知，本文所提出的最大能量回馈制动分配策略具有以下特点：

(1)在小制动强度下，电机制动能满足车辆制动需求，此时车辆采用纯电机制动，通过对前后轴制动力矩的分配减小电机通过再生制动传递能量到动力电池过程中的能量损失，提高制动能量回收效率。由图2可知，电机在小转矩的再生制动工况下能量传递效率较低，故总的制动力矩较小时由前轴进行制动。当前轴电机的最大制动力矩无法满足总的制动力矩需求时，则采用前后轴电机进行制动，选取总体效率最优的分配方案。

(2)随着制动强度增大，纯电制动无法满足车辆制动需求，车辆需要采用液压和电机的复合制动。此时车辆通过前后制动力的分配使得总的电机制动力矩达到最大，从而回收更多的能量。在复合制动的情况下，制动力分配基本与理想制动力分配相同，但在制动减速度为3～4m/s2时，存在制动力分配系数小于理想制动力分配系数的区间，使得后轴的电机制动力在约束条件允许的范围内达到最大。

4 仿真验证

为验证所提出的回馈制动控制策略的控制效果，基于Matlab/Simulink搭建了仿真模型，根据控制策略的特点进行了小强度制动工况、中等强度制动工况和循环工况的仿真分析，并与理想制动力分配策略进行了对比。

车辆初速度为35km/h，在附着系数为0.85的路面进行小强度制动，制动踏板开度为12%，仿真结果如图7所示。可知，车辆的制动强度较小，处于纯电机制动状态。采用理想制动力分配方案时，采用前轴和后轴电机进行制动，制动力按前后轴载荷进行分配；而采用本文所提出的控制策略时，车辆由前轴电机进行制动，后轴电机不参与制动，制动过程中电池的回收功率略大于理想制动力分配策略。

图7 小强度制动过程仿真结果Fig.7 Simulation results of small braking force

小强度制动过程仿真的能量流动分析结果如图8所示。制动过程可回收的制动能量为64.4kJ，在车速低于门限值时采用液压制动，高于门限值则采用电机制动，液压制动消耗的能量仅为2.35kJ，电机承担的制动能量为62.05kJ。采用理想制动力分配时电机的能量传递损失为17.75kJ，传递到电池的有效回收能量为44.3kJ。而采用最大能量回馈制动力分配时，能量传递损失降低为15.55kJ，电池回收到的制动能量为46.5kJ。在纯电制动工况下，所提出的策略有效降低了电机到电池的能量传递损失，制动能量回收效率由68.8%提高到72.2%。

图8 小强度制动过程能量流动分析Fig.8 Energy flow analysis of small braking force

车辆初速度为45km/h, 在附着系数为0.85的路面进行中等强度制动，制动踏板开度为33%，制动减速度为3.2 m/s2，车辆处于复合制动状态，仿真结果如图9所示。采用理想制动力分配时，前轴承担的制动力矩较大，电机制动力矩达到最大，不足部分采用液压制动进行补充，而后轴承担的制动力矩较小，采用纯电机制动，且未达到电机的最大转矩。采用本文所提出的策略时，在约束条件允许的范围内适当增大后轴承担的制动力矩，达到电机的最大转矩，故电机制动总力矩和回馈功率相比理想制动力分配策略有所增加。

中等强度制动过程仿真的能量流动分析结果如图10所示。制动过程可回收的制动能量为64.4kJ，在车速低于门限值时采用液压制动，高于门限值则采用电液复合制动。采用理想制动力分配时，液压制动消耗的能量为15.5kJ，电池承担的制动能量为99.9kJ，其中传递到电池的能量为64.7kJ，能量传递过程中的损失为35.2kJ。采用本文所提出的策略时，后轴制动力有所增加，前轴液压制动力减小，故液压制动消耗的能量减小为13.7kJ，电机传递过程的能量损失为35.1kJ，传递至电池的能量为66.6kJ。在中等制动强度的复合制动工况下，所提出的控制策略有效增加了电机承担的制动分量，而能量传递效率基本保持不变，能量回收效率由56.1%提高到57.7%。

图9 中等强度制动过程仿真结果Fig.9 Simulation results of medium braking force

图10 中等强度制动过程能量流动分析Fig.10 Energy flow analysis of medium braking force

为进一步检验所提出的回馈控制策略在实际使用工况中的能量回收效果，采用NEDC 工况循环进行了仿真分析，仿真结果如图11所示。NEDC循环包括了城市工况和郊区工况两个部分，进行能量回收效果分析时，分别对城市工况和整体循环工况进行了分析。

图11 NEDC工况循环仿真Fig.11 Simulation results of NEDC driving cycles

城市工况的回馈制动能量分析结果如图12所示。城市工况中的制动工况为中低速小强度制动，在车速高于门限值时采用纯电机制动。采用理想制动力分配策略时，电机的能量传递损失为200.8kJ，有效回收能量为501.2kJ。采用本文所提出的策略时，电机的能量传递损失为170.8kJ，有效回收能量提高至531.2kJ。故在城市工况下，所提出的控制策略通过合理分配制动力有效提高了电机制动的总体效率，减小了能量传递的损失，能量回收效率由68.3%提高到72.3%。

图12 NEDC城市工况制动能量分析Fig.12 Energy flow analysis of city (NEDC driving cycle)

NEDC循环工况的回馈制动能量分析结果如图13所示。郊区工况包含了高速工况，但制动过程均为小强度制动，在车速高于门限值时仍采用纯电机制动。采用理想制动力分配策略时，电机的能量传递损失为311.6kJ，有效回收能量为1070.8kJ。采用本文所提出的策略时，电机的能量传递损失为275.2kJ，有效回收能量提高至1107.2kJ。故在NEDC循环工况下，所提出的控制策略通过合理分配制动力减小了纯电机制动过程中能量传递的损失，能量回收效率由75.5%提高到78.1%。

图13 NEDC循环工况制动能量分析Fig.13 Energy flow analysis of NEDC driving cycle

综上，所提出的回馈制动控制策略在典型城市工况及典型循环工况下的制动能量回收效果均优于理想制动力分配策略，具有良好的实用效果。

5 结论

本文分析了分布式电驱动车辆回馈制动系统的性能特点及制动法规的约束，基于非线性规划求解，提出了最大能量回馈制动力分配控制策略，并与理想制动力分配策略进行了仿真对比分析。在小强度纯电制动工况下，所提出的控制策略能够通过优化电机制动力矩分配减小能量传递损失，提高能量回收效果；在中等强度的复合制动工况下，所提出的控制策略能够通过最大化电机制动力矩，增加回馈制动分量，提高能量回收效果；在NEDC循环工况下，城市工况的能量回收效率由68.3%提高到72.3%，整体工况循环的能量回收效率由75.5%提高到78.1%，所提出的回馈制动控制策略能有效提高实际使用工况下的能量回收效果，提高整车能量效率。

[1] Yimin Gao, Mehrdad Ehsani. Electronic braking system of EV and HEV - Integration of regenerative braking, automatic braking force control and ABS [A]. Future Transportation Technology Conference & Exposition[C]. 2001. 2001-01-2478.

[2] A Sakai, Y Sasaki, A Otomo. Toyota braking system for hybrid vehicle with regenerative system [J]. Journal of the Society of Automotive Engineers of Japan, 1998, 52 (11): 33-37.

[3] 郑宏宇，许文凯，刘宗宇，等(Zheng Hongyu, Xu Wenkai, Liu Zongyu, et al.). 四轮独立驱动电动汽车再生制动控制策略(Control strategy for regenerative braking for four-wheel-drive electric vehicle)[J]. 吉林大学学报(工学版)(Journal of Jilin University (Engineering and Technology Edition))，2013,43(3)：590-594.

[4] Wenkai Xu, Hongyu Zheng, Zongyu Liu. The regenerative braking control strategy of four- wheel-drive electric vehicle based on power generation efficiency of motors [A]. SAE 2013 World Congress and Exhibition [C]. 2013. 2013-01-0412.

[5] P Andrew, N Leonardo, G Patrick, et al. Optimal braking force allocation for a four-wheel drive fully electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers - Part I: Journal of Systems & Control Engineering, 2014, 228(8):621-628.

[6] Y He, X T Liu, C B Zhang, et al. A new model for state-of-charge (SOC) estimation for high-power Li-ion batteries [J]. Applied Energy, 2013, 101:808-814.

[7] F Tahami, R Kazemi, S Farhanghi. A novel driver assist stability system for all-wheel-drive electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2003, 52(3): 683-692.

[8] Bin Wang, Xiaoyu Huang, Junmin Wang, et al. A Robust wheel slip ratio control design combining hydraulic and regenerative braking systems for in-wheel-motors-driven electric vehicles[J]. Journal of the Franklin Institute, 2015, 352(2): 577-602.

Research on regenerative braking control strategy for distribute drive electric vehicle

WU Ling-fei1, 2, WANG Li-fang1, GOU Jin-fang1, ZHANG Jun-zhi3

(1. Key Laboratory of Power Electronics and Electrical Drives, Institute of Electrical Engineering,Chinese Academy of Sciences, Beijing 100190, China; 2. University of Chinese Academy of Sciences,Beijing 100049, China; 3. State Key Laboratory of Automotive Safety and Energy,Tsinghua University, Beijing 100084, China)

Regenerative braking control can improve the energy efficiency of distribute drive electric vehicle. The structure of the regenerative braking system, the characteristics of the motor and the constraint conditions of braking regulations are analyzed. A regenerative braking control strategy aiming at acquiring the maximum regenerative energy is proposed based on nonlinear programming. The characteristics of the regenerative braking control strategy are analyzed with consideration of the characteristics of the regenerative braking system. The regenerative energy efficiencies of typical braking conditions and driving cycle are analyzed through simulation. Results show that the proposed strategy can achieve better regenerative energy efficiency than ideal braking force allocation.

regenerative braking; distribute drive electric vehicle; baking force allocation; regenerative efficiency

2015-08-28

国家自然科学基金项目 (51475253)

伍令飞 (1987-), 男, 广东籍, 博士研究生, 研究方向为分布式电驱动车辆动力学控制; 王丽芳 (1971-), 女， 山西籍, 研究员, 博士生导师， 研究方向为电动汽车车用电源与充电系统。

U469.72

A

1003-3076(2016)09-0001-07