基于改进粒子群算法的含分布式发电配网孤岛划分

陆亚南， 施泉生

(上海电力学院经济与管理学院， 上海 200090)

基于改进粒子群算法的含分布式发电配网孤岛划分

陆亚南， 施泉生

(上海电力学院经济与管理学院， 上海 200090)

分布式电源(DG)在配电网中的比重越来越大，当配电网上级发生故障时，可以将配电网与上级电网断开，利用配电网内部的分布式电源为配电网中重要负荷提供持续稳定供电。为了最大化利用DG资源，同时保障重要负荷优先供电，本文提出了基于改进二进制粒子群的配电网孤岛划分方案。本文以二进制粒子群作为主程序，并对粒子进行组合变异，为了克服粒子群的早熟问题，采用模拟退火算法对粒子群进行优化。本文采用广度优先搜索算法对孤岛进行功率连通性校验。对不满足连通性要求的孤岛进行调整，最后找出最优方案。最后，采用IEEE69节点配电系统进行算例验证，算例结果表明本文算法的优越性。

分布式电源； 配电网； 孤岛； 粒子群算法； 稳定性

1 引言

随着传统电力系统联网规模的增大，大电网的事故故障极易大面积扩散，造成一系列连锁反应，最终导致电力系统全面崩溃。为了保障重要负荷的稳定供电，传统的配电网一般都备有备用电源[1]。现在，分布式电源(Distributed Generation，DG)大量并入配电网，其对电网的影响也越来越大。DG的接入位置、接入容量对提高DG的利用效率和增强配电系统的供电稳定性具有很大的影响[2]。当大电网发生故障时，若简单地将DG从配电网中切除，那么配电网的供电可靠性将会大大降低，DG的利用效率也大打折扣。IEEE1547-2003标准也明确规定不再限制发生故障时DG的使用，而是要鼓励通过技术手段实现DG的孤岛运行[3]。孤岛运行是指在配电网中，DG可以独立地向配电网系统的部分负荷供电。在系统稳定运行时，预先制定好孤岛划分策略，当大电网发生故障时，直接将配电网与大电网断开，按孤岛划分方案对部分重要负荷恢复供电[4]。制定孤岛划分方案时，主要考虑电网结构、DG的接入位置、发电特性以及发电容量等。对每个孤岛系统采取有效控制，可以确保其安全稳定运行。

随着配电网中DG比重的增大，如何提高DG利用效率以及增强重要负荷供电可靠性已经成为研究的焦点。可以利用微网技术和分布式电源，将配电网划分成若干个可以安全稳定运行的小系统。

文献[5]结合配电网的树状结构，将配电网的各点、各边都赋权，利用深度优先搜索算法从靠近电网末端开始搜索满足约束条件且尽可能大的孤岛。文献[6]结合图论知识，利用改进的Prim算法对配电模型进行遍历，寻找最小生成树。文献[7]以每个DG为中心向外扩展，在满足约束条件的前提下尽可能地融入1、2类负荷，但此算法没有考虑DG的运行特性，不能确保每个孤岛能够稳定运行。

本文提出二进制粒子群算法(Binary Particle Swarm Optimizer，BPSO)结合模拟退火算法以及组合变异算子，对每个划分方案进行更新、调节。算法充分考虑DG的运行特性，采用广度优先搜索算法对每个划分方案作电气连通性校验，并计算其适应度值，将适应度值与历史最优值比较，更新历史最优解，最后找出全局最优划分方案。算法最终目标为使得配电网中尽量多的负荷恢复供电，保障重要负荷优先恢复供电，并能够保障划分的每个小系统能够持续稳定运行。

2 孤岛划分的原则

电力系统中某个重要发电设备故障、某条重要输电线路跳闸、系统受到大的干扰等都需要形成能够提供稳定电能的孤岛系统[6]。可以利用孤岛内的DG，在满足稳定运行的基础上，使得尽量多的负荷恢复供电，同时保障重要负荷的供电可靠性。

孤岛划分是一个组合优化问题，其要满足以下两个原则：

(1)重要负荷优先原则。优先选择重要负荷恢复供电，即孤岛划分时应首先将1、2级负荷划入孤岛内。

(2)最大负荷恢复供电原则。为了提高DG的利用率，应该在满足功率平衡的基础上，尽量多地恢复故障负荷的供电，即尽可能地将负荷划分到孤岛内。

3 含DG的配电系统孤岛划分模型

3.1 含DG的配电网树模型

配电网的结构一般是闭环设计，开环运行。DG接入配电网，相当于配电网多了一个负功率的负荷支路，网络结构并没有发生明显变化。在不影响网络结构的基础上，可以对网络结构进行如下简化[8-10]：

(1)网络中接有DG的各个节点，将DG与该节点合并，节点的功率值变为PLi+PGi(PLi为负荷功率，PGi为接入节点的DG的功率)。

(2)可以将功率值为0的节点与其上一个节点合并，但配电网的结构不发生变化。

3.2 含DG的配电网孤岛优化划分的数学模型

当检测到大电网故障时，为了防止事故带来的一系列连锁反应，需要将配电网与外部电网断开。故障发生前，配电网与大电网的关系存在两种情况，一种是配电网向大电网输送电量，另一种是大电网向配电网输送电量。若是前一种情况，则故障发生后，可以直接将配电网与大电网断开，通过调节控制机制，使得配电网形成一个稳定运行的孤岛；如果是后者，即故障发生后，将配电网与大电网断开后，配电网发电量小于负荷总量，那么故障发生后需要对配电网进行优化划分，才能保证各个小系统稳定运行，同时保障重要负荷持续稳定供电。孤岛要稳定运行必须满足：①孤岛内DG的发电总量要大于孤岛内的负荷总量；②要尽可能保证重要负荷恢复供电；③孤岛内必须存在满足SDG(Stable DG，表示具有稳定输出功率的DG)&CDG(Controllable DG，表示可以通过控制改变其输出功率的DG)的DG，同时，要充分发挥DG利用效率。

目标函数为：

(1)

式中，lLi取值0或1，lLi=0表示第i个节点是断开的，lLi=1表示第i个节点是闭合的；hLi表示i节点负荷的权重[11]，本文1级负荷取hLi=1.0，2级负荷取hLi=0.1，3级负荷取hLi=0.01；PLi为第i节点上的负荷功率值；Cn为总节点数。

约束条件包括：

(1)功率平衡约束

(2)

式中，lGK取值0或1，lGK=1表示第k个DG包含在孤岛内，lGK=0表示第k个DG不包含在孤岛内；PGK表示第k个DG所能发出的功率上限；NG表示孤岛内DG的数量；NL表示孤岛内负荷节点的数量。

(2)连通性约束

(3)

(4)

(5)

式(3)中，lLg取值0或1，表示第Lg个DG是否包含在孤岛内，若包含在孤岛内则lLg=1，否则lLg=0，即式(3)表示孤岛内必须至少含有1个DG；式(4)与式(3)类似，lLd取值0或1，若第Ld个负荷包含在孤岛内则lLd=1，否则lLd=0，即式(4)表示孤岛内必须至少含有1个负荷；nLi-Lj=1表示节点i与节点j相邻，nLi-Lj=0表示节点i与节点j不相邻；G表示DG集合；I表示节点集合。

(3)DG类型约束

(6)

式中，Gp为具有稳定功率输出、同时又可以与调度中心进行通信的DG的集合，即CDG&SDG。

4 基于模拟退火的二进制粒子群优化算法

4.1 编码方式

线路中开关只有断开与闭合两种状态，因此可以用0、1分别表示线路中开关断开与闭合的两种状态[12]。粒子种群中，每个粒子表示一种划分方案，每个粒子的维数表示网络的开关节点个数。当大电网发生故障前，整个配电网络都是功率联通的。故障发生以后，为了使配电网中尽量多的负荷恢复供电且保障重要负荷的供电可靠性，需要对种群中的每个粒子进行功率连通性校验。本文采用广度优先搜索算法对开关闭合的线路(即编码为1的线路)进行功率连通性校验。功率连通性的标准为：每个孤岛中至少要存在一个满足SDG&CDG的DG和负荷。若孤岛内不存在满足要求的DG，则将该孤岛的所有节点编码全部置0；若孤岛内不存在负荷，即只存在DG，则将其对应编码节点置0，或将其划入相邻的具有功率连通性的孤岛中。

4.2 二进制粒子群算法

在二进制粒子群优化算法中，每个粒子的每个元素的位置分量x的取值只能是0或1，因此速度v不再表示位置变化的大小，它反映的是x取1的概率[13-15]。设粒子群为d维空间，则第i个粒子的位置、速度可以分别表示为Xi=[xi1,xi2,…,xid]、Vi=[vi1,vi2,…,vid]。pbest表示每个粒子的历史最优位置，记作[pi1,pi2,…,pid]；gbest表示全局历史最优位置，记作[pg1,pg2,…,pgd]。

基本公式定义如下：

(7)

(8)

式中，c1、c2为学习因子，通常取c1=c2=2.0；r1、r2为[0,1]之间的随机数；rand为[0,1]之间的随机数；S(vid)为sigmoid函数，S(vid)=1/(1+e-vid)；w为惯性权重，一般在0.4到1.2之间取值，文献[12]指出随着迭代次数的增加，w线性减少，将会大大改善算法的收敛性。其基本公式为：

(9)

4.3 模拟退火算法

模拟退火算法可以通过控制温度来控制算法的跳出局部最优解的能力。首先确定初始温度，然后随机选择一个状态的目标函数值作为最优解，当状态变成一个新的状态时，记录新状态的目标函数值。如果新的目标函数值比旧的目标函数值优秀，则以概率1接受新的状态，否则以概率Pr接受新的状态。只要模拟退火方法的初始温度取得足够高，并且温度冷却得足够慢，它就可以以概率1收敛于问题的全局最优值，同时，由于它以某种概率接受问题的劣质点，所以具有避免陷入局部最优的能力[16]。算法的求解过程如下：

(1)首先初始化温度t，随机产生初始解x，并计算x的目标函数值f(x)。

(2)在可行域中随机产生一个新的可行解x′，并计算其目标函数值f(x′)。

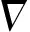
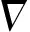
(10)

接收x=x′，其中random为[0,1]之间的随机数。

(4)tk+1=Ctk，k←k+1，其中C∈[0,1]。若迭代次数k大于最大迭代次数或收敛，则退出；否则，转步骤(2)。

4.4 基于模拟退火的二进制粒子群优化算法

本文提出改进的二进制粒子群优化算法以二进制粒子群优化算法作为主要运算流程，为了防止算法早熟陷入局部最优，本文加入模拟退火算法，同时为了增加种群的多样性，引入了交叉变异算子[17]。算法的寻优过程先随机产生初始群体，再通过式(7)和式(8)更新粒子的速度与位置；然后，对划分方案做电气连通性校验，并计算其适应度值；再对新粒子进行杂交变异以产生新的种群，对新种群的适应度值进行模拟退火运算来更新粒子的历史最优解。

在每次进化过程中，杂交运算采取轮盘赌操作选取一定数量的粒子，对被选取的粒子随机进行两两杂交，保持粒子总数不变。杂交后的粒子速度分别由以下公式得到：

(11)

(12)

式中，v为D维的速度向量；childk(v)和parentk(v)(k=1,2)分别表示新、旧粒子的速度。新粒子的速度对应的粒子位置由式(8)求得。

交叉变异以后，依据变异概率在种群中随机选取一些粒子来进行变异，以使种群跳出局部最优解。本文按高斯变异算子进行变异，用变异后的粒子速度代替原粒子的粒子速度，变异函数为：

mutation(v)=v(1+Gaussian(ν))

(13)

式中，Gaussian(ν)为以原点为中心，σ为设置参数的高斯变异，表达式为：

然后根据式(8)求得粒子速度对应的粒子位置。

本文算法首先进行全局搜索，利用式(7)和式(8)产生一组群体；再进行局部搜索，运用式(11)、式(12)和式(8)对新粒子进行交叉运算，采用式(13)和式(8)进行变异运算；然后通过模拟退火算法更新种群粒子的适应度值。每一次更新粒子种群都要采用广度优先搜索算法对新粒子进行功率连通性校验。反复迭代，直到达到最大迭代次数为止，其算法流程如下：

(1)初始化各参数：粒子数N，粒子维数D，最大迭代次数K，退火的初始温度t，温度的冷却系数C，变异概率Pm，学习因子c1和c2。

(2)随机生成N个初始粒子。

(3)对新生成的粒子进行电气连通性校验，采用3.1节的方法对不满足要求的孤岛进行调节。

(4)计算各个粒子的适应度值，若粒子中某个孤岛不满足功率平衡约束，则需要进一步判断是否满足：

(14)

式中，CL为可以保证孤岛稳定运行的孤岛的允许减载量。当满足式(14)时，则可由式(1)得出该孤岛的适应度值，检验下一个孤岛；若不满足，则将该粒子的适应度值置为负的无穷大，检验下一个粒子； 将目前的粒子位置作为个体的历史最优解pbest，适应度值为pbest_fit，并将该种群中最好的位置作为全局最优解gbest，全局最优适应度值为gbest_fit。

(5)采用式(7)和式(8)更新粒子的速度和位置。

(6)对新产生的粒子进行功率连通性校验，并计算其适应度值fitness；比较fitness、pbest_fit，如果fitness>pbest_fit，则将fitness赋给pbest_fit，同时更新pbest。

(7)将式(6)中经过功率连通性校验的新粒子群以轮盘赌操作选取一定数量的粒子形成子种群，并将子种群中的粒子按下面操作产生一个新种群：

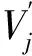
(15)

(16)

(8)对于新的粒子种群，由变异概率Pm挑选出一定数量的粒子进行如下变异产生新的粒子：

(17)

(9)若迭代次数k>K，则输出最优解；否则转到步骤(5)。

5 算例分析

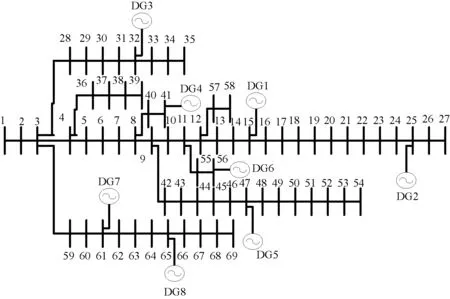
图1 包含DG的69节点配电系统Fig.1 69-bus distribution system with DGs

本文采用IEEE69节点配电系统做算例验证，该系统的参数见文献[10]。本文在IEEE69节点配电系统的不同母线处分别接入不同类型的分布式电源，DG的接入位置如图1所示，各分布式电源的参数见表1。本文设定每个孤岛的允许减载量为孤岛总负荷的2%。为了区分负荷的重要程度，本文将负荷分为三类，分类情况见表2。

表1 DG参数

表2 负荷节点类型

当大电网发生故障时，将配电网与主网断开，采用本文算法对配电网进行孤岛划分，使得尽量多的负荷恢复供电的同时，保障重要负荷的持续稳定运行。基于模拟退火的二进制粒子群中，算法参数的设置如下：粒子维数D=69；粒子种群N=100；惯性权重系数起始值wstart=0.4，最终值wend=1.2，粒子的速度取值范围为v=[-4,4]，粒子的加速系数c1=c2=2；模拟退火算法中设定初始温度t=106，降温系数lam=0.95；算法最大迭代次数K=200。算法求得的划分结果如图2所示。

图2 包含DG的配电网孤岛划分方案Fig.2 Optimal island partition scheme of distribution system integrated with DGs

从图2中可以看出，共搜索到3个孤岛。孤岛1包含节点1～20、28、40～52、55～69，即断开边20-21、28-29、52-53；孤岛中包含DG1、DG7，满足CDG&SDG，所以可以稳定运行，孤岛总负荷为2427kW，功率裕量为-27kW，允许减载量为48.54kW。孤岛2包含节点22～26，即断开边21-22、26-27；孤岛中DG2满足CDG&SDG，孤岛可以稳定运行，孤岛总负荷为47.3kW，功率裕量为2.7kW，允许减载量为0.946kW。孤岛3包含节点30～35，即断开边29-30；孤岛中DG3满足CDG&SDG，孤岛可以稳定运行，孤岛总负荷为39.5kW，功率裕量为0.5kW，允许减载量为0.79kW。

图3为运用本文算法在寻优过程中最优粒子适应度值的变化曲线。可以看出，最优适应度值为596.44；本算法能够在开始后较少迭代次数内找到局部最优解，在25次迭代左右就可以找到全局最优解。

图3 最优粒子的运动轨迹Fig.3 Best moves recorded during search process using proposed algorithm

为了进行比较，本文采用文献[5]的孤岛划分方法对69配电系统进行划分，划分的结构如图4所示。可以看出配电系统被划分为4个孤岛，其中DG5没有被划分进去， DG的利用效率没有本文算法好。本文算法的结果与文献[5]的划分结果分析见表3。

图4 文献[5]配电网孤岛优化划分方案Fig.4 Optimal island partition scheme of distribution system by method of Ref.[5]

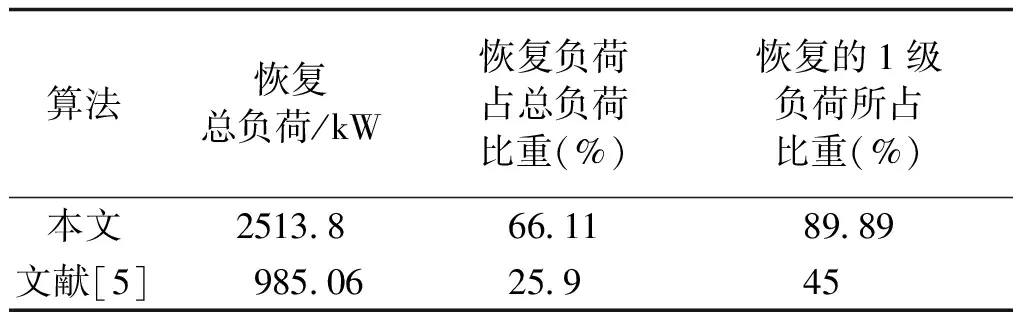
算法恢复总负荷/kW恢复负荷占总负荷比重(%)恢复的1级负荷所占比重(%)本文2513866118989文献[5]9850625945

6 结论

当大电网发生故障时，配电网需要尽快与大电网断开连接，然后根据配电网中DG的运行特性，以及负荷的供电可靠性要求对配电网进行孤岛优化划分，从而使得尽量大范围的负荷能够持续稳定恢复供电，并保证重要负荷的优先供电。本文采用的孤岛划分算法主要有三部分：首先利用二进制粒子群算法对配电系统进行全局搜索；然后利用广度优先搜索算法对种群中的每个粒子即每个孤岛划分方案进行功率连通性校验；最后引进模拟退火机制，跳出局部最优解，避免陷入早熟，并且采用杂交变异算子，使得种群更具有多样性。利用本文算法求得的孤岛划分方案能够保障每个孤岛稳定运行，而且尽可能地保障重要负荷的供电，同时负荷恢复率也比较高。随着智能电网的发展，当大电网发生故障时，本文提出的配电网孤岛划分策略具有一定的参考价值。

[1] 谢夏慧，汪沨，陈奇朋 (Xie Xiahui, Wang Feng, Chen Qipeng)．含分布式电源的配电网关键负荷保障方法 (A method to ensure power supply reliability for key load in distribution network containing distributed generation) [J]．电网技术(Power System Technology)，2013，37(5)：1447-1453．

[2] 刘宗歧，鲍巧敏，孙春山, 等 (Liu Zongqi, Bao Qiaomin, Sun Chunshan, et al.)．基于改进Kruskal算法的含分布式发电的配网孤岛划分算法 (Islanding algorithm of distribution system with distributed generations based on improved Kruskal alogorithm) [J]．电工技术学报(Transactions of China Electrotechnical Society), 2013，28(9)：164-171．

[3] 李承熹(Li Chengxi)．配电网中分布式电源并网优化运行与孤岛划分问题研究(Research on grid-connected optimal operation and island partition for distributed generation in distrbution network)[D]．杭州：浙江大学(Hangzhou: Zhejiang University). 2013.

[4] Caldon R，Stocco A，Turri R．Feasibility of adaptive intentional islanding operation of electric utility systems with distributed generation [J]．Electric Power Systems Research，2008，78(12)：2017-2023.

[5] 丁磊，潘贞存，丛伟 (Ding Lei, Pan Zhencun, Cong Wei)．基于有根树的分布式发电孤岛搜索(Searching for intentional islanding strategies of distributed generation based on rooted tree) [J]．中国电机工程学报 (Proceedings of the CSEE)，2008，28(25)：62-67．

[6] 董晓峰，陆于平 (Dong Xiaofeng, Lu Yuping)．基于改进Prim算法的分布式发电孤岛划分方法 (Islanding algorithm for distributed generators based on improved Prim algorithm) [J]．电网技术(Power System Technology)，2010，34(9)：195-201．

[7] 易新，陆于平 (Yi Xin, Lu Yuping)．分布式发电条件下的配电网孤岛划分算法(Islanding algorithm of distribution network with distributed generators) [J]．电网技术(Power System Technology)，2006，30(7)：49-54．

[8] 刘健，毕鹏翔(Liu Jian, Bi Pengxiang)．复杂配电网简化分析与优化(Simplified analysis and optimization of complex distribution network)[M]．北京：中国电力出版社(Beijing: China Electric Power Press)，2002．

[9] Mesut Bara，Felix Wu．Network reconfiguration in distribution systems for loss reduction and load balancing [J]．IEEE Transactions on Power Delivery，1989，4(2)：1401-1407．

[10] Baran M E, Wu F F． Optimal capacitor placement on radial distribution systems[J]．IEEE Transactions on Power Delivery，1989，4(1)：725-734．

[11] 倪程捷，房鑫炎，胡子衔 (Ni Chengjie, Fang Xinyan, Hu Zixian)．基于递归子问题树法的含DG配电网最优孤岛搜索(Optimal island search of distribution network with DGs based on recursive sub-problem tree algorithm) [J]．中国电力(Electric Power)，2014，47(2)：42-47．

[12] 杨建军，战红 (Yang Jianjun, Zhan Hong)． 基于图论的改进遗传算法在配网重构中的应用(Application of the improved genetic algorithm based on graph theory in distribution network reconfiguration) [J]．电力系统保护与控制 (Power System Protection and Control), 2010，38(21)：122-125．

[13] Kenney J，Eberhart R C．A discrete binary version of the particle swarm algorithm [A]. 1997 IEEE International Conference on System, Man, and Cybernetics [C]．Orlando，USA，1997. 5：4104-4108．

[14] 徐义春，肖人彬 (Xu Yichun, Xiao Renbin)．一种改进的二进制粒子群算法(An improved binary particle swarm optimizer) [J]．模式识别与人工智能(Pattern Recognition and Artificial Intelligence), 2007，20(6)：788-793．

[15] Y Shi，R C Eberhart．A modified particle swarm optimizer [A]．IEEE International Conference of Evolutionary Computation[C]．Anchorage，AK, USA，1998. 69-73.

[16] 高鹰，谢胜利 (Gao Ying, Xie Shengli)．基于模拟退火的粒子群优化算法(Particle swarm optimization algorithms based on simulated annealing) [J]．计算机工程与应用 (Computer Engineering and Applications)，2004， 40(1):47-50.

[17] 欧阳武, 程浩忠，张秀彬, 等 (Ouyang Wu, Cheng Haozhong, Zhang Xiubin, et al.)．基于随机生成树策略的配网重构遗传算法(Genetic algorithm based on random spanning trees in distribution network reconfiguration) [J]．高电压技术(High Voltage Engineering)，2008，34(8)：1726-1730．

Islanding algorithm of distribution system with distributed generations based on improved particle swarm algorithm

LU Ya-nan, SHI Quan-sheng

(College of Economics and Management, Shanghai University of Electric Power, Shanghai 200090, China)

The proportion of DG in the distribution network is growing. When the fault in power network occurs, the power supply for key load in the distribution network can be sustained by DG after the distribution network and the power network is separated. To maximize the use of DG and ensure the power supply for key load, a new strategy for island partitioning based on the improved binary particle swarm algorithm is proposed in this paper. This paper takes the binary particle swarm algorithm as the main program, and takes the particle combined and mutated. To overcome the premature problem of particle swarm algorithm, simulated annealing algorithm is used to optimize the particle swarm algorithm. In this paper, the connectivity of single island power is verified by the breadth-first search algorithm. Adjusting the island which does not meet the requirement of connectivity, finally the optimal scheme is found. The effectiveness of the proposed method is verified by simulation results of IEEE 69-bus system.

distributed generation; distribution network; island; particle swarm algorithm; stability

2015-08-10

上海市教委科研创新重点项目(12ZS161)、上海高校人文社会科学重点研究基地——“一带一路”能源电力管理与发展战略研究中心资助项目(WKJD15004)

陆亚南(1991-)， 男， 江苏籍， 硕士研究生， 研究方向为电力系统、 电力经济与管理； 施泉生(1961-)， 男， 上海籍， 教授， 硕士， 研究方向为电力经济与管理。

TM734

A

1003-3076(2016)07-0017-07