探讨高三数学教学中教材的二次开发



探讨高三数学教学中教材的二次开发

◇江苏潘晓霞

教材的二次开发是指教师在备课的过程中,根据教学目标的要求对教材进行适当的加工和调整,也可以适度增、删教学内容,选用合适的教辅资料来配合自己的教学,满足学生的学习需求．数学教材的二次开发是新课程改革的关键,可以使教师从根本上转变过去那种讲解教材的思想观念．高三数学教学中教材的二次开发尤为重要．

1改变不合适的教学情境

数学教学需要一定的教学情境,教学情境的设计能够激发学生的求知欲望,体会数学与生活之间的联系．但有时教材所提供的情境对学生而言是陌生的,需要教师根据实际情况把教材中不合适的教学情境换成学生所熟知的事例,这样能够引起学生的学习兴趣,进而促进对新知识的理解．

案例1苏教版选修2中平均变化率的教学情境的引入.

教师可以用讲故事的方式开场:美国的科学家曾经做过这样一个实验,把一只青蛙直接扔进沸腾的油锅中,青蛙反应敏捷,能够迅速跳出油锅,安全逃生．过了1小时,他们在一个同样大小的铁锅中放了很多凉水,把刚才那只青蛙放进锅里,它安然自得地在锅中游来游去,然后对水慢慢地加热,当这只青蛙终于忍受不了水的温度想要跳出去时,它已经全身瘫痪,没有一点力气了．这是我们大家都很熟悉的哲理故事,其反映的数学知识同样值得我们深思：从数学的角度看,为什么同样一只青蛙在2次实验中会有不同的结果呢？然后据此引入要学的平均变化率内容．

2对跳跃性太大的知识进行衔接

由于篇幅限制,数学教材浓缩了重要知识点,一部分例题没有详细的解题步骤,这使学生在理解例题时会产生思维障碍．因此教师要协调好学生与教材之间的障碍,对于一些跳跃性太大的知识点和例题进行思维上的连接和拓展,通过对教材的二次开发来传达教师的思维过程,为学生的理解进行搭桥,不仅要使学生知其然,还要知其所以然．

案例2关于三角函数正切线的教学.

如何把第一象限α的正切用有向线段来表示.

当角α的终边处于y轴的右端时,在这个角的终边上取一个点T(1,y′),那么tanα=y′/1=y′=AT(A是圆和x轴正半轴的交点)．

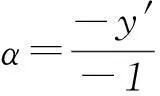
图1　　　　　　　　　　图2

如图1、2所示,有向线段AT就是角α的正切线．

但在实际教学中,学生常会产生这样的疑问:

1) 当角α的终边处于y轴的右端时,为什么要取点T(1,y′)?

2) 当角α的终边处于y轴的左端时,为什么要在这个角的终边的反向延长线上取点,为什么不直接取点T(-1,y′)?

数学教材在处理这个问题时,直接把结论阐述给了学生,并没有解释为什么要这样取点,这样取点的合理性在哪里.这之间有一些跳跃性的成分,学生很难一下子理解,这些地方就需要教师对教材进行二次创作．在实际教学中,教师不能直接对着教材讲解,需要对同学们不理解的地方作出解释,对于第1)个问题要从tanα=y/x定义出发,找出横坐标为1的点,那么纵坐标就是α的正切,这样写是为了使步骤更简洁．对于第2)个问题,教师要顺着学生的思路进行解释,如果直接取点T′(-1,y),设点A(-1,0),那么有向线段AT′就是α的正切线,这样虽然也能解释通,但是这样取点的话就与AT的情形不一致了,为了表述上的一致性,才在这个角的终边的反向延长线上取点．这样的解释学生容易理解．可见，尊重学生的思维,着重解释一些跳跃性的知识，也是对教材的二次开发．

教材是教育专家们智慧的结晶,具有权威性和指导性,那么教师在教学时应如何灵活地使用教材？教师要根据考试大纲的需要对教材内容进行适当的删减和调整,在认真研读教材的基础上对教材进行二次开发．只有这样才能收到良好的教学效果．

(作者单位：江苏省丹阳市第六中学)