基于强占优先M/M/1模型的应急通信系统呼叫性能分析方法
[余翔 吴浩 徐欣]
基于强占优先M/M/1模型的应急通信系统呼叫性能分析方法
[余翔 吴浩 徐欣]
摘要
在应急通信系统中,服务器对到达呼叫的平均响应时间是衡量其性能的一项重要指标。文章在详细分析SIP服务器工作原理的前提下,提出一种基于强占优先M/M/1模型的服务器呼叫性能分析方法,通过与无优先级的M/M/1排队模型的呼叫平均响应时间比较,发现具有强占优先权的M/M/1模型更能够满足实际应急通信系统对呼叫快速接入的需求。
关键词:应急通信 SIP服务器 平均响应时间 M/M/1 强占优先
余翔
男,重庆邮电大学。博士,教授。主要研究方向为宽带无线通信。
吴浩
男,重庆邮电大学。硕士研究生,主要研究方向为应急移动通信。
徐欣
女,重庆邮电大学。主要研究方向为计算机技术。
1 引言
呼叫管理服务器是应急通信系统的核心模块之一。当网络出现阻塞或者同一时段呼叫过多时,由于服务器自身并发处理呼叫的性能限制,导致呼叫等待时间过长。针对此问题,当前已有学者提出一些理论分析方法,如文献[1-2]提出了基于M/M/1和M/M/c的排队模型理论分析方法,对其呼叫中心SIP服务器性能进行分析和论证;文献[4]结合铁路列车调度需求提出M/G/1模型性能分析方案;文献[3]基于马尔可夫模型,主要利用SIP代理服务器的状态转移概率预测服务器呼叫性能的分析。但是以上文献对于呼叫模型的建立与分析主要基于传统的先到先服务排队规则,而在突发应急现场,尤其在紧急事件发生的状况下,该规则已不能满足现实应急通信系统对呼叫快速响应和接入的要求。
基于此,本文提出基于强占优先M/M/1模型的服务器呼叫性能分析方法,在详细分析SIP服务器工作原理的前提下,重点对无优先级的M/M/1呼叫排队模型和具有优先级别的M/M/1呼叫排队模型的呼叫处理性能进行研究分析,分别得出两种模型的性能分析结果,通过对比分析发现具有强占优先权的M/M/1模型更加符合现实应急通信系统的需求,从而为实际应急通信系统呼叫管理提供参考。
2 SIP服务器工作原理
SIP服务器的工作流程如图1。用户代理(User Agent,UA)即应急移动终端实体,可通过交换会话请求和会话响应发起或中止会话。UA分为发起会话请求的用户代理客户端(User Agent Client,UAC)和接收并返回请求响应的用户代理服务器端(User Agent Server,UAS)。SIP服务器是UAC和UAS之间的中间实体,负责接收UAC发起的会话请求并解析SIP消息,获得UAS的相关信息并将会话邀请信息转发给UAS。
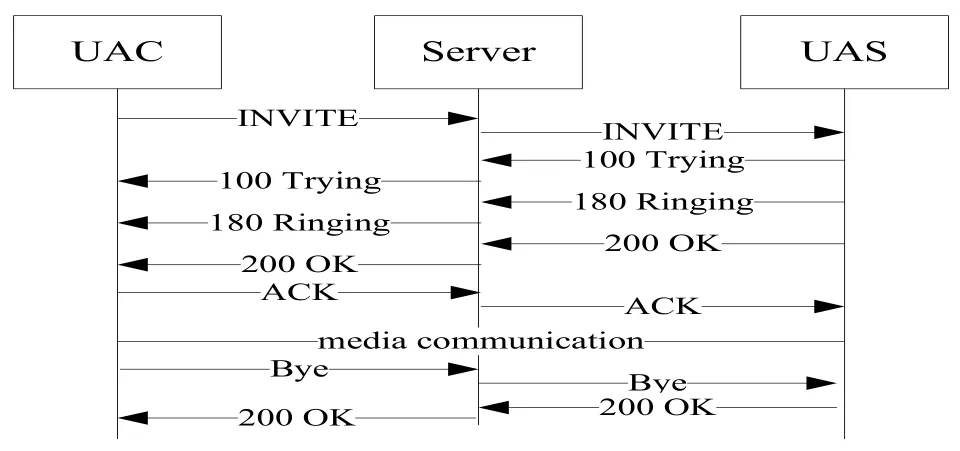
图1 SIP代理服务器工作流程
当服务器收到UAC发起的SIP会话请求后,首先对收到的SIP消息进行解析,在得到UAS的地址信息后将该会话邀请转发给UAS。如果UAS接受UAC的会话邀请,则向SIP服务器返回200OK数据包,SIP服务器此时向UAC转发200OK数据包,表示会话请求成功。UAC接着向服务器返回ACK确认数据包,服务器转发ACK确认数据包给UAS,会话建立。会话结束后,双方通过服务器转发Bye数据包结束会话。
3 呼叫处理过程分析
3.1无优先权M/M/1模型分析
在应急通信系统中,终端发起的SIP呼叫信息到达服务器的时间间隔是相互独立、互不影响的,在不区分优先级的情况下,可将系统模拟为如图2的M/M/1排队系统,该系统具备如下特点:1)呼叫按参数为λ的泊松分布到达;2)呼叫到达时间间隔和服务器对呼叫的服务时间均服从负指数分布,平均服务率为µ。
M/M/1排队系统是一个生灭过程,其状态流图如图3。
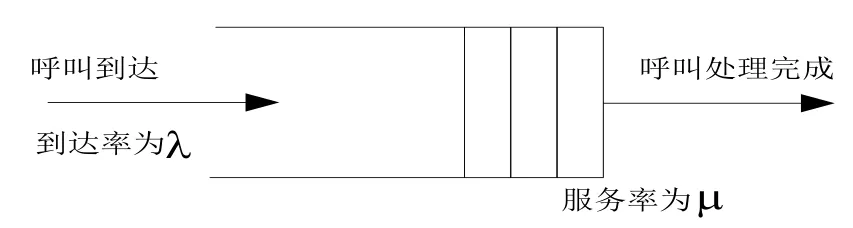
图2 基于M/M/1的呼叫排队模型
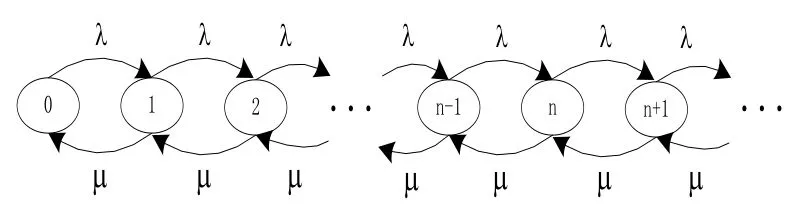
图3 M/M/1排队模型状态流图
其中,状态n表示系统内有n个呼叫,服务器正忙,有n1−个呼叫排队等待。
根据图3可列出系统状态转移概率pn(t)满足的微分方程如下,其中n≥1。
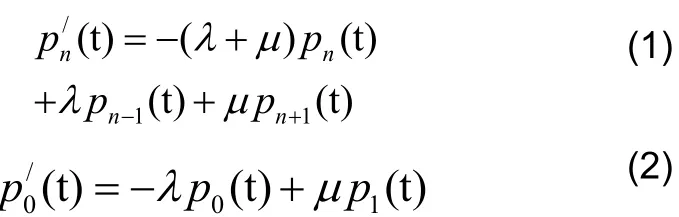
对于M/M/1模型,令服务强度:ρ= λ/µ
则当ρ<1时,服务器处理过程能达到平稳状态,即系统存在唯一平稳分布,记为,此时可将上述公式改为:
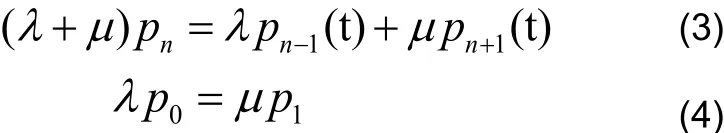
其中p0为系统服务器空闲的概率,由上可计算出M/M/1模型下系统的平均队长:
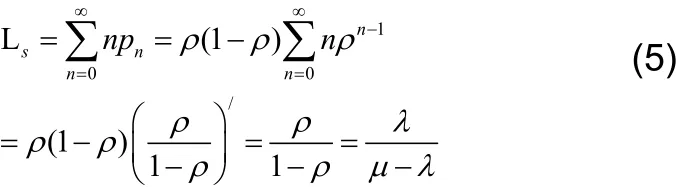
应用Little定理,可得每个SIP呼叫信息在系统中的平均逗留时间:

此时可求出系统内的平均呼叫等待队长:
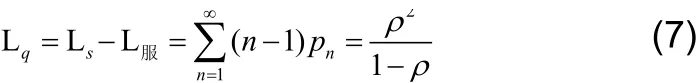
其中,L服为正在被服务器处理的呼叫数目均值。因被服务的呼叫数或为0(服务器空闲)或为1(服务器忙),它们对应概率为p0= 1− ρ及ρ,因此得到:
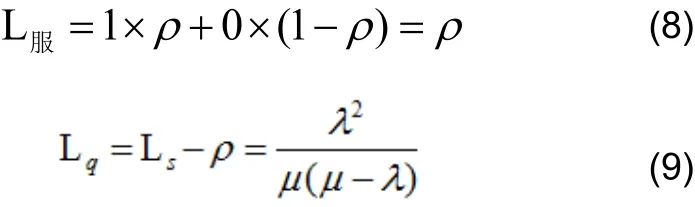
再次应用Little定理,求出呼叫平均等待时间,即系统对呼叫的平均响应时间:
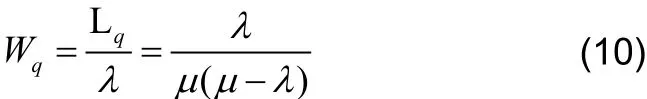
由上述推导公式可以看出,系统平均呼叫等待队长和系统对呼叫的平均响应时间均依赖于呼叫到达率λ和服务器对呼叫的平均服务率。采用无优先级的M/M/1模型对系统服务器性能进行分析,需要知道服务器对SIP呼叫消息的平均服务时间µ−1和终端呼叫发起的平均时间间隔λ。结合国家科技重大专项课题“基于TD-LTE/TDSCDMA的应急通信系统研发”项目对呼叫小组每组应急终端数目满足16或16整数倍,且组内成员数不能太多的具体需求,本文设每秒到达服务器的呼叫数为16,32,48,64,80和96,设定服务器对SIP呼叫消息的平均服务时间µ−1为10ms。由此可得到无优先级M/M/1模型的呼叫服务器性能分析结果如表1。

表1 无优先级M/M/1模型性能分析结果
从表1可看出,基于 M/M/1模型的SIP呼叫处理服务器的呼叫平均响应时间与SIP呼叫消息的到达率呈线性关系,当呼叫数增加时,呼叫的平均等待队长和平均响应时间均相应增加。当终端发起的呼叫数目不足80个,即呼叫强度不超过80%时,呼叫的平均响应时间不超过40ms,服务器性能良好。但当终端发起的SIP消息数目进一步增加时,呼叫的平均响应时间急剧增加,达到200ms数量级,显然已经不能满足应急通信对呼叫快速响应和接入的需求。
3.2具有强占优先权的M/M/1模型分析
在突发应急现场,尤其在紧急事件发生的状况下,先到先服务规则已不能满足现实应急通信系统对呼叫管理的实时性要求。从表1中也能看出,在呼叫达到率很高时,无优先级M/M/1服务器模型的呼叫平均响应时间大幅增加,服务器性能急剧下降。基于此,本节将对应急通信呼叫进行优先级划分,并对具有强占优先级的M/M/1服务器模型性能进行分析。
对具有强占优先权的M/M/1排队系统假设如下:
(1)救援人员分高级救援人员和一般救援人员两个等级。根据呼叫性质的不同,将呼叫分为紧急呼叫和一般呼叫。规定同一性质的呼叫高级救援人员享有较高优先级。特别地,规定一般救援人员的紧急呼叫优先级高于高级救援人员发起的一般呼叫。因此,本节将服务器接收到的呼叫信息从高到低分为四个优先级:高级救援人员发起的紧急呼叫,一般救援人员发起的紧急呼叫,高级救援人员发起的一般呼叫和一般救援人员发起的一般呼叫。
(2)令iλ为第i级呼叫的平均到达率,i =1,2,3,4,且均服从泊松分布。服务器为每一级呼叫的服务时间S均服从参数为µ的负指数分布,即平均服务时间
对于具有强占优先的M/M/1排队系统,由于系统仅有一个呼叫处理服务器,当具有较高优先权的呼叫到达时候,如果正被服务的是具有较低级别优先权的呼叫,则该呼叫将被中断服务,重新回到队列中排队等待。因此,若具有最高级别的呼叫到达系统,除具有同样最高级别的呼叫正被服务需要等待外,其他情况均可立即接受服务。假设具有最高级的呼叫到来时(即高级救援人员发起的紧急呼叫),系统可认为不存在其他级别的呼叫,此时系统可视为呼叫到达率服从参数为1λ的泊松分布,呼叫的服务时间服从参数为µ的负指数分布的M/M/1排队系统。记分别为第i级呼叫在系统中的平均排队等待时间和平均逗留时间,由3.1节推导容易得出第1级呼叫在系统中的平均排队等待时间Wq1和平均逗留时间Ws1分别
对于第2级呼叫(即一般救援人员发起的紧急呼叫)到达时,由于存在强占优先权,可认为系统中只有第1,2级优先级的呼叫,记为第1,2级呼叫在系统中每一呼叫的平均逗留时间,易知:
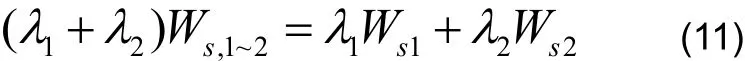
由此得:
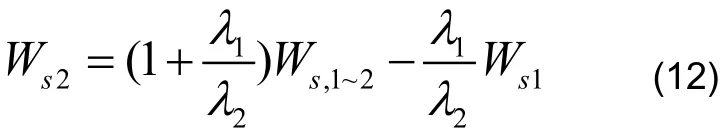
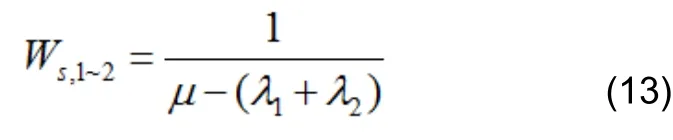
进而求出:
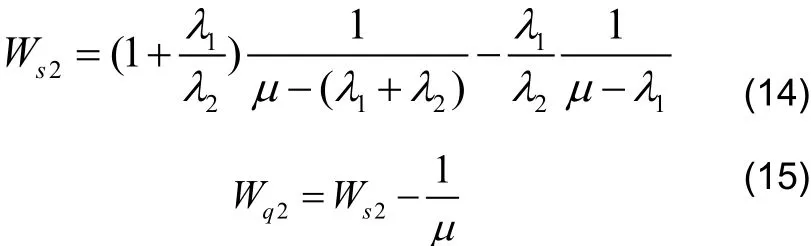
同理可求出:
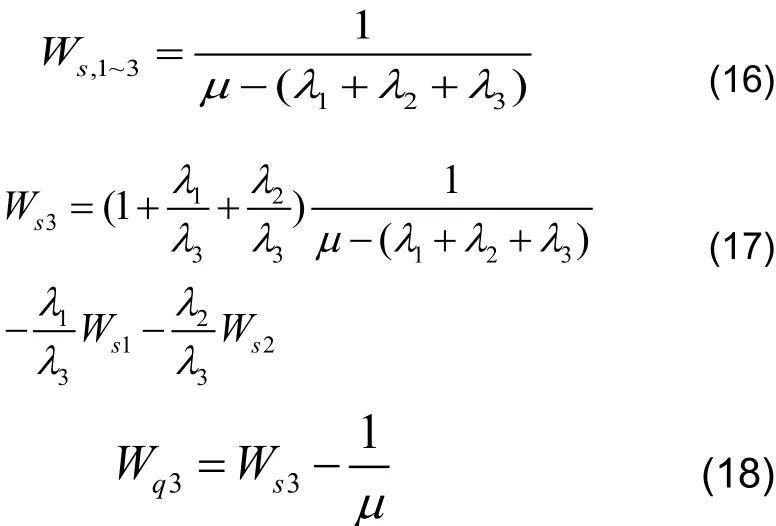
归纳得到第n级(1< n≤ N)呼叫的平均逗留时间和平均排队等待时间分别为:

同样,设每秒到达服务器的呼叫数为16或16的整数倍。以16人的救援小组为例,规定每组含2名高级救援人员,其余为一般救援人员。规定紧急呼叫占个人发起呼叫总数的20%,即当每秒到达的呼叫数为16时,计算得到:。设定服务器对SIP消息的平均服务时间为10ms。由此可得到具有强占优先的M/M/1模型的系统SIP服务器性能如下表2。
由表2可以得到,具有强占优先的M/M/1模型SIP呼叫处理服务器的呼叫平均响应时间与SIP呼叫消息的到达率呈线性关系,且具有高优先级别的呼叫的平均响应时间低于具有低优先级的呼叫的平均响应时间。当终端发起的呼叫数目不足80个,即呼叫强度不超过80%时,仅一般救援人员的一般呼叫的平均响应时间接近50ms。当呼叫发起数进一步增加时,除第四级呼叫的平均响应时间较长外,其余等级呼叫均在10ms以内,这显然更加符合应急通信对快速建立呼叫的要求。
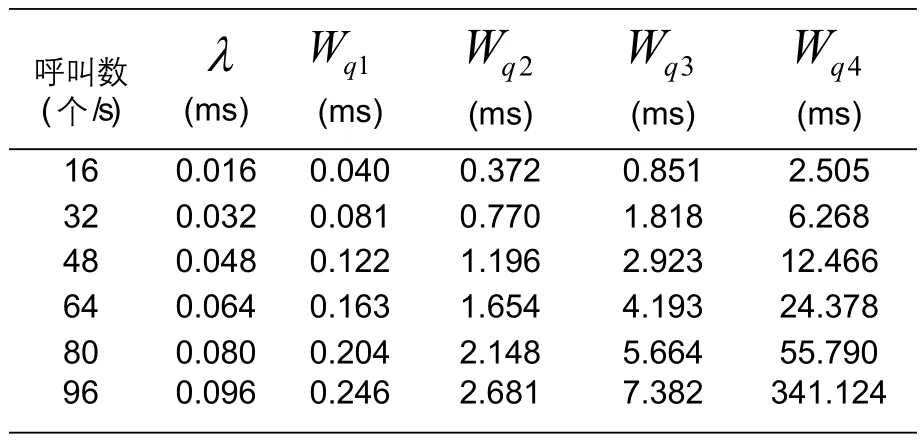
表2 具有强占优先的M/M/1模型性能分析结果
3.3两种模型性能比较
为更直观对两种模型进行性能对比,将表1和表2的呼叫平均响应时间呈现在图4中。
从图4可以看出,在对呼叫进行优先级划分后,除第四级呼叫外,具有高优先级的呼叫平均响应时间明显低于相同呼叫数的低优先级呼叫和无优先级呼叫的平均响应时间。在相同呼叫数时,第四级呼叫的平均响应时间高于无优先级呼叫的平均响应时间,这是以牺牲低优先级呼叫的服务效率为代价来提高高优先级呼叫服务效率的。在呼叫强度不超过80%时,两种排队模型的呼叫平均响应时间均满足应急通信对呼叫快速接入的要求且具有强占优先级的M/M/1模型服务器性能更优。考虑到呼叫强度接近为1的情况并不常见,本节建立的服务器呼叫处理过程排队模型可作为应急通信系统呼叫管理技术的有效参考。
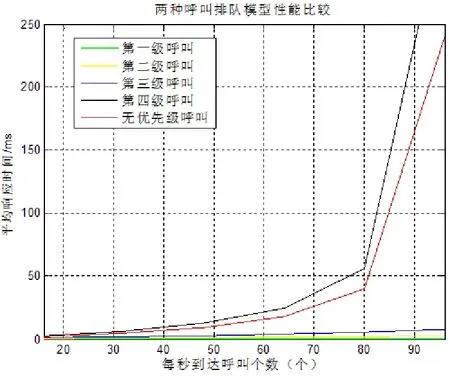
图4 两种M/M/1模型性能比较
4 结束语
本文提出了基于强占优先M/M/1模型的服务器呼叫性能分析方法,并分别对无优先级的M/M/1模型和具有强占优先权的M/M/1模型进行性能分析,对比了两种模型得到的呼叫平均响应时间。在相同的呼叫到达率的前提下,通过比较分析发现:具有强占优先权的M/M/1模型的呼叫性能更加适合实际应用的需求。随着应急通信系统的拓展和推广,下一步工作需要对多服务器的体系结构进行研究和分析。
参考文献
1Subramanian S V,Dutta R.Measurements and analysis of M/M/1 and M/M/c queuing models of the SIP proxy server[C]//International Conference on Computer Communications & Networks.IEEE Computer Society,2009:1-7
2Subramanian S V,Dutta R.Performance and scalability of M/M/c based queuing model of the SIP proxy server-a practical approach[C]//Telecommunication Networks and Applications Conference(ATNAC),2009 Australasian.IEEE,2009:1-6
3Hong Y,Huang C,Yan J.Analysis of SIP retransmission probability using a Markov-Modulated poisson process model[C]//Network Operations and Management Symposium(NOMS),2010 IEEE.2010:179-186
4周贵,刘峰.基于排队论的列调SIP代理服务器性能分析[J].计算机工程,2014,40(8):233-236
收稿日期:(2015-12-23)
DOI:10.3969/j.issn.1006-6403.2016.03.010

