频率源的相位噪声对雷达系统性能的影响

杨　俊，许　强

(中国船舶重工集团公司第723研究所，扬州 225001)



频率源的相位噪声对雷达系统性能的影响

杨俊，许强

(中国船舶重工集团公司第723研究所，扬州 225001)

摘要：频率源是雷达系统的重要组成部分，从相位噪声概念、成因讨论了本振相位噪声对雷达系统的影响因素，并得出在满足系统要求前提下合理的相位噪声指标参数。

关键词：频率源； 相位噪声；改善因子；动态范围

0引言

频率源是雷达系统的重要组成部分，现代雷达为了获得好的相参处理增益及对杂波的抑制能力，大都要求频率源输出的信号频率具有好的相干性和稳定性。而频率稳定度是频率源设计的关键，因此研究频率稳定度十分必要。相位噪声是频率源的一项非常重要的性能指标,它对电子设备和电子系统的性能影响很大。从频域看，它分布在载波信号两旁，按幂律谱分布。

用这种信号不论作为发射激励信号,还是给接收机提供本振信号以及各种频率基准时,这些相位噪声在解调过程中都会和信号一样出现在解调终端,引起基带信噪比下降。在理论界，作为频率稳定度时域表征的阿仑方差和由巴纳斯提出的表征频域的幂律法被国际广泛推崇，许多理论研究结果引用了这些概念。单边带相位噪声功率谱密度十分清晰地反映了造成频率不稳定的各种噪声、干扰分量的频率位置与电平大小。下面从频率稳定度、相位噪声概念出发，讨论频率源的相位噪声对雷达系统性能的影响因素。

1频率稳定度分析[1]

频率稳定度是指在固定时间间隔内，频率准确度的变化，代表了一个频率保持恒定的能力。频率稳定度分长期稳定度、短期稳定度和瞬时稳定度。对雷达接收系统而言，瞬时频率稳定度对于雷达技术性能的影响更直接，因为雷达的多普勒频率处理往往是在雷达的一个周期之间进行的，本文所研究的相位噪声就是这种瞬时频率稳定度。

不考虑初始相位，一个理想的频率源输出的本振信号可以表示为：

(1)

式中：V0为信号幅度；ω0为信号角频率；φ0为信号固定相位，均为常数。

这样信号在频域为一根纯谱线,在时域看其波形周期为一常数。 实际信号总会存在幅度起伏A(t)和相位起伏φ(t),因而瞬时输出信号可写为：

(2)

式中:Ec,ω为标称幅度和标称角频率;A(t) 为瞬时幅度起伏;φ(t) 为瞬时相位起伏。

对于高稳定频率源，|A(t)|≪V0，|φ0|≪1，一般调幅噪声A(t)总可以忽略,式(2)可简化为:e(t)=V0cos[ω0t+φ(t)]。则瞬时相位Ψ(t)为:

(3)

因而瞬时频率f(t)为:

(4)

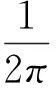
(5)

由于存在闪变噪声，使得频率源都不是真正的平稳随机状态，因此标准方差是发散的，失去了理论意义。实际是用计算器在有限的时间间隔内测量有限次数，这样测量值和标准方差有一定的误差。为了在N次采样测量中能求得真实值，都采用阿仑方差σα(t)表示：

(6)

式中:t为采样时间;M为采样次数。

2相位噪声定义[1-2]

现代雷达频率源通常都是由基准源经倍频、分频、混频等方法产生所需频率信号(称直接合成)或通过锁相环来产生要求的信号(称为间接式合成)。不管是哪一种合成方法都会产生附加噪声,加之基准源本身固有的噪声和频率变化过程中理论噪声的变化, 这些噪声会对信号频率和振幅进行调制，故实际的信号频谱总有一定的宽度。图1所示为信号相位噪声示意图。

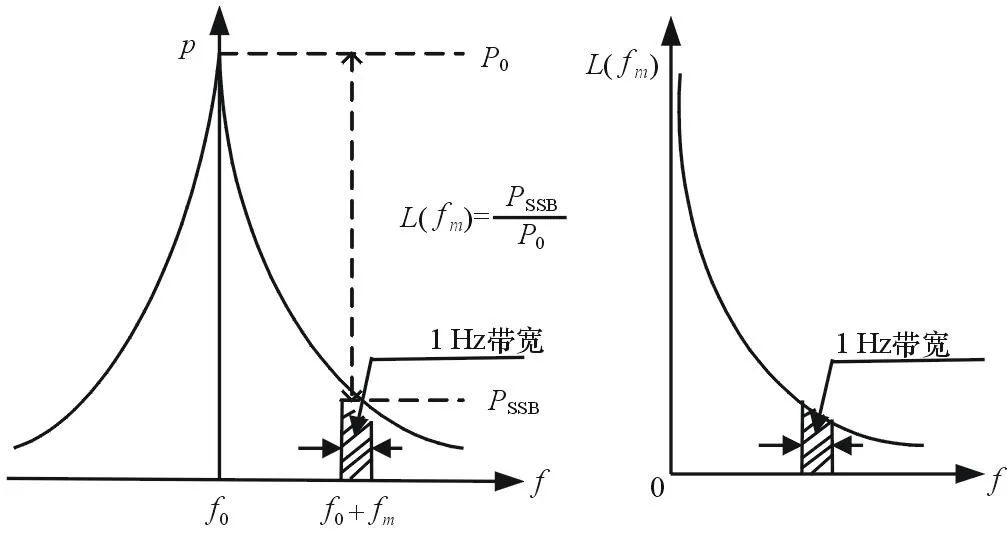
图1　相位噪声定义

相位噪声是指在系统内各种噪声作用下引起的输出信号相位的随机起伏。表征相位噪声的方法有以下几种：单边带相位噪声、频谱起伏谱密度、相位起伏谱密度、相对频率起伏谱密度及两点阿仑方差。其中单边带相位噪声是最常用的表征相位不稳定的方法，它可以直接用频谱仪测试，前提是频谱仪的本振相位噪声比被测件相位噪声好。美国国家标准定义SSB相位噪声为：偏离载波频率fm在1Hz带宽内一个相位调制边带的功率PSSB与载波功率PO之比，单位是dBc/Hz，其表达式为：

(7)

式中：ΔΦrms为相位变化的均方根值。

如果用SΔΦ(fm)表示相位噪声功率谱密度，则有：

(8)

其对数表示形式为：

SΔΦ(fm)|dB=10lg[L(fm)]+3

(9)

则相位噪声功率谱密度和频率起伏谱密度之间的关系为：

(10)

3相位噪声对雷达系统性能的影响

3.1频率源的相位噪声改善因子计算方法[2-3]

雷达改善因子的定义是：动目标显示系统输出的信号杂波功率比(Si/Ci)和输入信号杂波功率比(S0/C0)之比值，即：

(11)

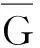
之所以要取平均,是因为系统对不同的多普勒频率响应不同,而目标的多普勒频率在很大范围内分布之故。

实际上，雷达信号处理滤波器输出的杂波剩余是由各种因素引起的，它可以写成：

C0= C0扫描+ C0杂波起伏+ C0系统不稳+ C0量化噪声+…

(12)

因此，系统总的改善因子I也是由各种因素共同决定的，即：

(13)

对改善因子形成影响的主要因素是天线扫描、杂波内部运动、雷达系统各主要部件工作不稳定和模/数变换器量化噪声等几方面。因此，要使雷达对杂波具有好的改善因子，必须合理分配各种因素的改善因子，降低各种因素对改善因子的影响。

3.2相位噪声对MTI改善因子的影响[3-4]

雷达系统本身不稳定的因素主要有：发射机、本振、相参振荡器频率不稳和定相不稳引起的相位不稳、脉冲幅度不稳。

相参视频信号用公式表示为：

u=KdUz=KdUk+KdUrcosφ

(14)

上式表明：u由直流分量KdUk和信号成分KdUrcosφ组成。

Δu=u1-u2=

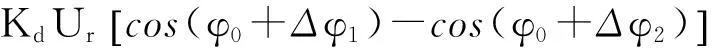
(15)

sinφ0与相位抖动无关，仅与目标距离有关，为方便讨论，设sinφ0=1，通常Δφ1与Δφ2为相互独立的随机变量，所以Δu也是随机的。剩余杂波为：

(16)

(17)

(18)

若发射不稳，相邻2次发射脉冲的频率差为Δf，由于Δf0抖动,在脉冲宽度τ内的相位平均变化则为：

(19)

同样，本振和相参频率不稳定的频率抖动为ΔfL和Δfk，则引起的相位变化分别为：

(20)

(21)

式中：tR为固定杂波返回雷达所需要的时间。

3.3计算实例

频率稳定度为10-7，选取f0=1 000MHz，fL=1 030MHz，fk=30MHz，τ=2μs，杂波源距雷达150km,分别计算出I值如下：

ΔfT=10-7×1 000×106=100Hz

ΔfL=2×10-7×1 030×106=206Hz

ΔfK=2×10-7×30×106=6Hz

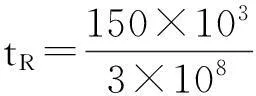
3.8dB

根据上面的计算可知：I相位不稳=3.8dB，相当于改善因子为2.4倍。显然信杂比改善太小，无法实际应用。其主要原因是IL太小，即本振源稳定度对改善因子的限制起主要作用。因而首先要提高其频率稳定性。常将本振放置在恒温槽内，并选用超低噪恒温晶体振荡器，这样才能提高总的改善因子。若使IL=34.5dB,则要求本振频率稳定度为2.9×10-9，可得I相位不稳=31.5dB。

3.4相位噪声对动态范围的影响

在雷达系统的应用中，所有的超外差接收机都采用一次或二次混频将输入的射频信号变换到中频。为了适应复杂电磁频谱的环境，对接收机提出了各种高要求技术指标，如高灵敏度、大动态范围及好的选择性等。

尤其是在雷达一体化电子侦察设备中，要求接收机能同时处理进入接收机的强、弱信号。当接收频率附近有强干扰信号时，强、弱信号进入混频器会造成接收机系统灵敏度降低甚至堵塞。这是因为本振相位噪声的存在，功率较强的信号在下变频之后没有得到抑制，同时本振的相位噪声也会在混频时传递给大信号的中频信号输出，压制了小信号混频之后中频输出信号的信噪比。

如图2所示，当本振信号的相位噪声差时，就有可能导致小信号在中频输出时被大信号的噪声边带所淹没；如果本振信号的相位噪声较好，则在中频输出端仍然可以提取出混频后的弱信号。

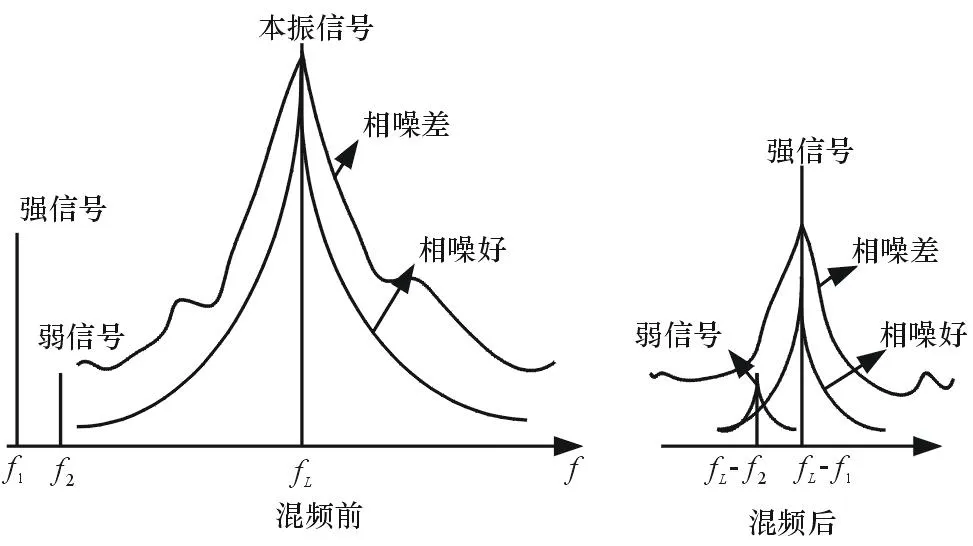
图2　相位噪声对动态范围的影响

从接收机动态范围的角度考虑，在系统要求的最小分辨率处，本振的相位噪声应优于系统的接收

机动态范围，并留有一定余量。

例如，对于X波段雷达接收系统要求的最小分辨率为10 kHz，动态范围为60 dB，则本振的相位噪声至少要达到65 dBc@10 kHz。考虑到小信号参数测量、解调时所需要的信噪比等因素，一般要求本振的相位噪声达到表1所示。

表1　X波段本振典型相位噪声

4结束语

相位噪声和频率源的稳定度已成为现代雷达的一项重要指标。通过以上分析可知，本振相位噪声对接收机性能具有重要影响，而本振对信号的恶化，则只能通过改善本振相位噪声来减小其影响。在以后的工程设计中，针对不同的系统要求，对频率源提出了合理的相位噪声指标要求。

参考文献：

[1]弋稳.雷达接收机技术[M].北京：电子工业出版社,2005.

[2]JOHN G C.本振相位噪声及其对接收机性能的影响[J].和新阳,雷颖蓓译.空间电子技术，2003(1):4- 13.

[3]SKOLNIK M I.雷达手册[M].王军，林强，米慈中，等译.北京：电子工业出版社，2003.

[4]樊海博，李敏.PD 雷达 MTI 改善因子影响因素分析[J].火控雷达技术，2005,25(2):83-88.

Influence of Phase Noise of Frequency Source on Radar System Performance

YANG Jun,XU Qiang

(The 723 Institute of CSIC,Yangzhou 225001,China)

Abstract:Frequency source is the important component of radar system.This paper discusses the influence factors of local oscillation phase noise on the radar system from the concept and cause of phase noise,and educes logical phase noise index parameters on the premise of meeting the system requirements.

Keywords:frequency source；phase noise；improvement factor；dynamic range

DOI:10.16426/j.cnki.jcdzdk.2016.01.012

中图分类号：TN957.51

文献标识码：A

文章编号：CN32-1413(2016)01-0058-04

收稿日期:2015-10-09