模糊PID控制在单相光伏逆变电源中的应用

陈圆圆

(商丘师范学院 河南 商丘 476000)

模糊PID控制在单相光伏逆变电源中的应用

陈圆圆

(商丘师范学院 河南 商丘 476000)

文章对PID控制和模糊控制的优缺点进行了分析，并提出了将两者结合组成模糊自整定PI双闭环控制，并对控制器进行了设计，最后通过仿真，证明了该方法的有效性。

单相光伏逆变电源；模糊自整定PI双闭环控制；数学模型；仿真

1 引言

PID控制一种比较成熟的控制算法，在逆变电源中有着广泛的应用。该控制算法具有较快的动态响应特性和较强的鲁棒性[1]。将PID控制引入单相光伏逆变电源，不失为一个好方法。然后光伏逆变电源随着光照、温度的变化而在不断变化，因此是一个时变系统，且在高频阶段，所建的数学模型误差较大，参数难以实时整定，很显然，如果采用传统的PID控制误差较大。模糊控制不需要精确的数学模型，多应用于时变的多变量、强耦合、非线性的复杂系统，由于控制的简便性使其得到了广泛的应用[2]。如果将模糊控制与PID控制相结合，用模糊控制解决在高频阶段逆变系统数学模型不精确和参数不能实时整定的问题，便能够进一步提高系统的逆变效率。

2 逆变电源系统数学模型

逆变系统采用全桥逆变结构，假设功率开关为理想器件，且开关频率远大于LC的频率，则系统可以等效为一个二阶系统。如图1所示。

图1 逆变系统等效图

Vi为单相全桥逆变器输出电压；为Lf等效电阻；Lf为滤波电感；iLf为滤波电感电流；为Cf等效电阻，Cf为滤波电容；Vcf为电容电压；为负荷电流。假设系统所带负荷为阻性负荷，且阻值为R，可得到复频域的数学表达式P（ s）。

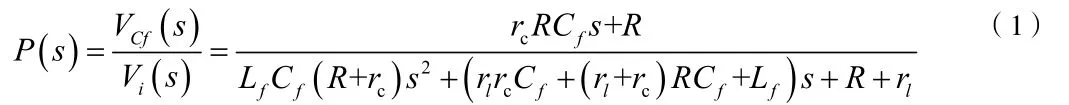
令采样频率与开关频率相等，根据面积等效原则，以逆变器输出电压在每个周期的PWM波平均值作为采样值，并将逆变桥看作零阶保持器，便可将1式离散化，得到其离散数学表达式P（z）。

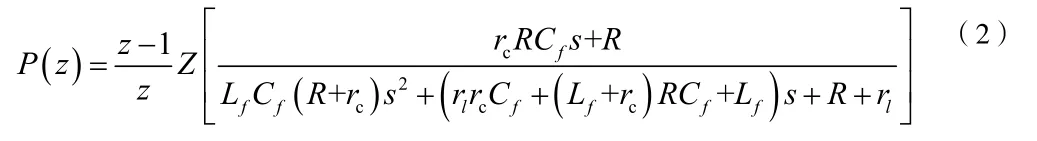
3 PID双闭环控制

PID控制在单相光伏逆变电源中有着广泛的应用，其结构简单，调节能力强。这种控制方法需要有精确的数学模型，且参数不能自动调整。早期的光伏逆变电源系统中，往往采用的是单环的控制系统，即只将电压引用了控制系统。这种采用单电压环控制的系统，当负载发生变化时，特别是接非线性系统时，性能往往满足不了要求。

为了提高系统性能，将电感电流引入控制系统，和前面所说的电压环构成双闭环控制。双闭环控制系统利用外部电压环的电压误差控制内环的电流，通过电流的调节，令输出电压稳定在给定值上，从而提高系统的动态响应能力。

4 模糊控制

在实际应用系统中，存在大量的时变的非线性系统，为了解决这些复杂的，难以建出精确数学模型的系统的控制问题，出现了模糊控制。模糊控制基于经验，采用数字化的方法，解决了复杂系统控制精度难的问题，是当今智能领域发展最为迅速的控制算法之一。模糊控制模拟了人类的思维，但与其他智能算法相比，却比较简单，因此在时变的多变量、强耦合、非线性的复杂系统中得到了广泛的应用。

如果将模糊控制与PID双闭环控制相结合，就可以解决前面所说的，在高频阶段，单相光伏逆变系统数学模型不精确，参数不能在线整定的问题。

5 模糊自整定PI双闭环控制

模糊自整定PI双闭环控制，是一种将模糊控制与PI双闭环控制相结合的复合控制策略。它利用模糊控制进行自动在线的整定PI参数，从而提高系统的控制性能。

由于单相光伏逆变电源系统的输出受温度、光照的影响，且其负荷类型多变，因此要想得到良好的控制效果，必须对PI参数进行在线调整。通常采用的是在线辨识整定的方法，然而此种方法不适用于非线性、时变性的单相光伏逆变电源系统。将模糊控制引用，从而完美的解决了这个问题。模糊自整定PI双闭环控制器的结构如图2所示。

图2 模糊自整定PI双闭环控制器结构图

r为给定的电压值，y为系统输出电压值，e和ec分别为偏差和偏差变化率，将偏差和偏差变化率同时输入到模糊控制器中，模糊控制器通过模糊化、近似推理和清晰化后，得到ΔKp、ΔKi两个修正量，并将他们送到PI控制器中，从而达到在线整定的目的。

7.1 接阻性负载系统仿真图 (R=5Ω)：

图3（a） PI双闭环接阻性负载

图3（b） 模糊自整定PI双闭环接阻性负载

7.2 接感性负载系统仿真图

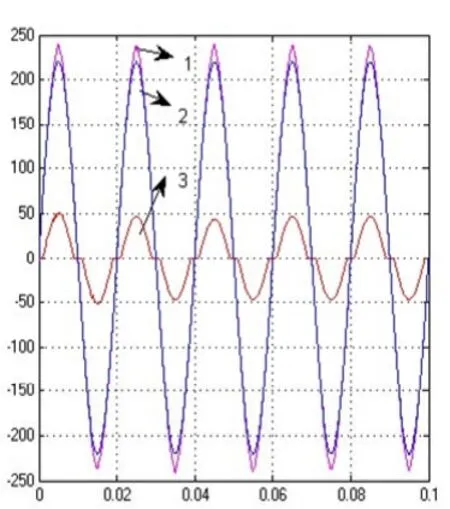
图4（a） PI双闭环接感性负载

图4（b） 模糊自整定PI双闭环接感性负载

从仿真图中可以看出，无论接阻性负载还是感性负载，模糊自整定PI双闭环控制都比PI控制器的精度高。

[1]高军，黎辉，杨旭，王兆安.基于 PID控制和重复控制的正弦波逆变电源研究[J].电工电能新技术，2002(1):1-4

[2]诸静.模糊控制理论与系统原理[M].北京:机械出版社,2005,8.

[3]吴晓莉,林哲辉.MATLAB辅助模糊系统设计[M].西安:西安电子科技大学出版社,2002:65-86.

K928

A

1007-6344（2016）10-0089-02