谱混合模型方法优化及其在海洋水团分析与水交换研究中的应用

宋　军，刘玉龙，李　静，2，郭俊如，牟　林，姚志刚，李希彬

（1.国家海洋信息中心，天津　300171；2.上海海洋大学　海洋科学学院，上海　201306；3.国家海洋局海洋减灾中心，北京　100194；　4.中国海洋大学　教育部物理海洋学重点实验室，山东　青岛　266100；5.国家海洋局天津海洋环境监测中心站，天津　300457；6.国家海洋局空间遥感与应用研究重点实验室，北京　100081）



谱混合模型方法优化及其在海洋水团分析与水交换研究中的应用

宋军1，4，刘玉龙1，李静1，2，郭俊如3，6，牟林1，姚志刚4，李希彬5

（1.国家海洋信息中心，天津300171；2.上海海洋大学海洋科学学院，上海201306；3.国家海洋局海洋减灾中心，北京100194；4.中国海洋大学教育部物理海洋学重点实验室，山东青岛266100；5.国家海洋局天津海洋环境监测中心站，天津300457；6.国家海洋局空间遥感与应用研究重点实验室，北京100081）

摘要：优化了谱混合模型（Spectral Mixture Model，SMM）分析方法，提出了谱混合模型方法中两个关键参数的一般优化方案。优化后的方法能够对大量的数据样本进行快速聚类分析，并通过求解概率密度函数确定不同聚类之间的混合区域。以该方法在海洋水团以及水交换中的应用为例，详细阐明了谱混合模型方法的工作原理及过程。在谱聚类方法基础上建立的谱混合模型分析法，避免了传统模糊聚类分析方法的不足，即使在物理量的散点数据分布呈现广泛连续性时，仍然能够抓住数据时空分布的主要变化方向，其在水团的辨别、水团边界以及水交换混合区的分布及其变化规律的研究中具有广泛的应用。关键词：谱聚类；谱混合模型；海洋水团分析；水交换；模糊数学；温度-盐度图

水团是源地与形成机制相近、具有大体相同的物理、化学和生物特征及变化趋势，并与周围水体有明显差异的水体（张绪东等，2004）。不同的水团，其温度、盐度、密度等要素也不同，声学、光学性质也有一定的差异，这些对于海军潜艇的活动、水雷布设、水下通讯及监视，都有巨大的影响。在不同水团接壤、交汇的边界水域，大多是有名的渔场。因此，对水团以及水团之间的交换混合区域给出准确的鉴别，并对其变化给出迅速的判断和预测，能够对军事、渔业和水产事业与决策提供重要的信息保障。举例来说，中国的近海，大部分地处中纬度温带季风区，四季交替明显，季节变化显著；深度不足200m的浅海，区域宽阔，岛屿棋布，岸线复杂；东部海域有强大的黑潮及其分支，西部有众多的江河径流入海（浦泳修，1981）。因而中国沿海水域水团分布复杂多变，寻找一种快速有效的水团鉴别方法具有重要的科学意义与实际意义。

Sverdrup等（1942）首次使用温度-盐度图（T-S图）进行水团分析，Miller等（1950）则首次应用T-S图研究了水团的划分问题。近年来，基于T-S图的隶属函数方法（Lietal，2004）与聚类分析方法（Su etal，1989）被广泛用于研究水团的划界与混合问题。但是隶属函数方法只对特定的T-S曲线形状有效，并且当使用同一方法应用到不同海域的时候，经常需要大量且复杂的调整工作才能使其适合研究的需要。经典的聚类分析方法有着更一般的应用方法，但当T-S分布呈现广泛的连续性时，该方法很难抓住T-S曲线的主要变化方向。此外，以上两种方法在处理大量数据点集的情况时，效率都非常低下。近年来，随着观测数据与数值模型结果数据的日益庞大，且可用于水团分析的要素从温度、盐度转为多种要素，作为NP-hard问题的水团分析过程使经典的水团分析方法已不能满足实际研究的需要。

鉴于以上现状，宋军（2010）将图论中的最新研究成果——谱聚类方法（Spectral Clustering，SC）引入到海洋科学的研究当中，并基于此构建了可解决上述传统水团分析方法问题的谱混合模型方法。本文将对该方法的构建过程与应用方案进行详细的描述，并对模型中的两个关键参数给出了具体的优化方案。

1算法综述

为了更清楚地解释这一方法，我们首先定义集合P = {P1，…，Pn}为所有目标研究区域的数据点，其中n为所有数据点的数量。集合M = {m1，…，mk}则被定义为所有聚类的集合，以满足我们将上述n个数据点（P）划分为k个聚类（M）的描述需要（Song，2011）。应该说明的是，为使本研究具有实际的物理意义，聚类的数目k应该小于数据点的数目n，并且每个点有且只属于一个聚类。谱混合模型的计算过程主要包括三大步：第一步，使用谱聚类方法将所有目标数据点划分为任意需要数目的聚类。所有的聚类以及其重心位置将在这一步得到确定；第二步，基于我们构造的概率密度函数，将得到每一个数据点Pi∈P映射到所有参与相互混合作用的聚类mi⊂M的隶属概率；第三步也是最后一步，任意两个属于上一步考虑范围的聚类之间的交换区将得到定义，并且以此为基础，任意多个聚类的混合区域也将得到定义。不同于经典的混合模型，由于谱混合模型基于谱聚类方法，其基于数据点的连续程度考虑了数据点的主要分布方向，无论这一方向是直线的还是任意曲线的。此外，在计算概率密度函数时，谱混合模型还考虑了每一个聚类的势力范围，而并非仅使用各聚类重心的位置作为计算混合区域分布和位置的标准。在分析水团混合的研究中，各聚类的势力范围是指其拥有的数据点的数目以及这些数据点的平均分布密度。在本研究当中，由于整体数据点的分布密度差异不大，取各聚类拥有的数据点的数目作为其势力范围的指标。

1.1谱聚类

谱聚类（Spectral Clustering，SC）是一个21世纪刚刚发展起来的最新的聚类方法，但其明显的优越性使其本身成为最热门的研究学科之一（Von，2007）。谱聚类基于图像分析理论，在计算机科学，特别是人工视觉系统（Jitendra et al，2001）和机器学习（Shietal，2000）等人工智能方面的研究中，甚至在与计算机结合紧密的最前沿的其他学科，比如生物化学（Menschaert et al，2009）的研究中，都有着广泛的应用。由于谱聚类方法不仅考虑了所有目标数据点之间的差异性，而且考虑了整体数据的分布结构及其连通性，使其更容易抓住主要矛盾，该方法表现出较高的计算效率，这一点在数据量（包括数据点的数目和参数空间亦即区分不同数据点所使用的性质参数的数目）较大的时候更加明显（Andrew etal，2002）。更重要的是，谱聚类可以更容易地得到全局最优解，从而避免了经典聚类分析方法使结果在凸型数据区域的计算中陷入局部最优的问题（Luo etal，2003）。简单来说，谱聚类方法将所有的目标数据点Pi∈P考虑为一个多维无向连通图G的顶点（如图1所示）。在本研究中，顶点来自模型结果中对应的每个计算网格的水质点数据。G是一个无方向但各边具有不同权重的图（加权图），我们使用一个半正定的，对称权重的矩阵A（Aij=Aji≥0）来表示任意两点Pi和Pj之间的相似性，这个相似性也即是图G中各边的权重。这里我们使用Aij来表示两个数据点Pi和Pj在其参数空间下的距离。举例来说，边A23表示顶点P2与P3之间的相似度。在图G （P，A）中，求解聚类分析的问题可以等价为求图G的最小‘割权’问题。

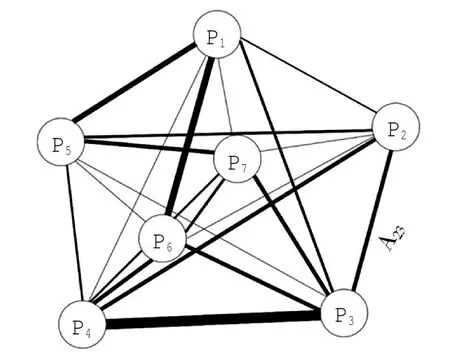
图1　用于表示各点之间相似度的无向连通加权图G（P，A）。其中A中各边的权重（图中由各边的粗度表示）表示两个顶点之间的相似度大小

为了避免任意孤立点从图中被分离出去，如大多数的相关研究一样，这里也采用一个升级的割权定义来代替上面的割权定义，称这一升级的割权为标准化割权（Ncut），其被定义为如下形式：

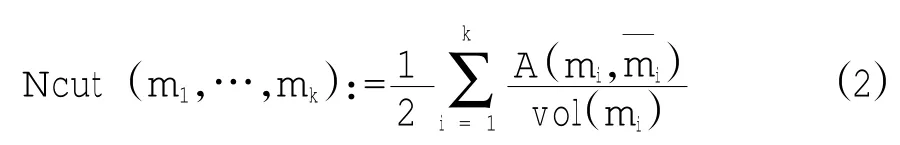
其中，vol（mi）=∑i∈miAij。为求得上述标准化割权的最小值，谱聚类算法是目前为止被证明的最直接和有效的方法（Von，2007）。对于属于集合Rl（字符R通常被用作表示实数集，其上标则表示此实数集的维数）的目标数据点集合P，将P划分为k个聚类，其完整的谱聚类算法被简单的描述如下：

1）构造亲和度矩阵A∈Rn×n，在本研究中，我们使用高斯相似函数来定义A：

其中，σ为尺度参数，当计算pi与pj两点间的相似度Aij时，它决定了随两点间距离的增加而造成的衰减率。虽然这里有很多方法可以自动的优化参数σ（Von Luxburg，2007），但在本研究中，由于所有的数据都已进行了标准化处理，所以该参数被简单地设为1。

2）定义一个对角矩阵D，其中Dii等于矩阵A中第i行所有数值的总和：

3）定义一个拉普拉斯矩阵L，这是一个半正定的矩阵：

4）求解矩阵L，得到最小的k个特征值（λ1，…，λk）和这k个特征值对应的特征向量（，…，）；

5）构造目标矩阵O=（（x）1，…，（x）k）∈Rn×k，其每一列分别等于上一步求得的各个特征向量；

6）对矩阵O的每一行分别做标准化，使其拥有统一的单位标准，并由此构造出矩阵Q∈Rn×k如下：

7）将矩阵Q的每一行看作每个对应的数据点，这就意味着矩阵Q是一个有N个数据点，并且每个数据点有k个参数属性的矩阵。最后使用K-means或其他经典的聚类分析方法对这一新构造的数据点集进行聚类分析，进而得到聚类集合M以及其相应的每个聚类和聚类的重心。

在本研究中，使用经典的K-means聚类分析方法来完成最后的一步运算。简单来说，K-means聚类分析的核心算法可以描述为以下5步。如果希望提高其在计算机中的计算速度，可以参考Lai等（2009）发展的快速K-means聚类计算方法。

1）随机地给出任意k个聚类的重心坐标；

2）分别计算每个数据点到这些聚类重心的距离。本研究采用欧式相空间距离公式来计算这一距离；

3）将每个点归入距离其最近的聚类重心所代表的聚类中，这意味着第一次将所有的点分为了k个聚类；

4）通过计算每个聚类中所有数据点坐标的平均值，重新计算每个聚类的重心坐标；

5）重复做以上第2步到第4步的运算，直到所有的聚类集合都不再发生变化。至此，就得到了最终的分类方案和每个聚类的重心。

为了更直观地展现传统的K-means聚类分析法与谱聚类分析法在实际研究中的不同，本文分别用两种方法对黑潮与东中国海地区的水团进行了聚类分析（如2所示）。图2清楚地显示出直接采用K-means聚类分析方法（图2a）和谱聚类方法（图2b）的一个结果对比图。很显然后者更能表现出黑潮水与东中国海陆架水的水团分布情况，从而能够定义一个两者之间的水交换带。该结果主要是由于在东中国海，垂直于黑潮流向的温度盐度变化趋势要远大于沿着黑潮流向方向的变化趋势造成的。更多类似于K-means方法与谱聚类方法在处理不同数据集的结果对比，可以参照Cai等（2005）的工作，其研究结果表现了谱聚类方法相对于传统聚类方法的绝对优势。

图2　两种聚类方法对经过标准化的100 m层的温度-盐度（T-S）数据进行聚类分析的结果图

2.2概率密度函数

为了定义一个模糊混合区域，我们首先需要知道每个数据点多大程度的隶属于每个需要考虑参与交换的聚类。基于上面谱聚类分析得到的每一个聚类的重心坐标，将构造一个概率密度函数以计算每个数据点投影到相应的所有聚类的概率。具体算法构造如下：

1）对任意数据点Pi∈P，定义disi，kk（kk∈[1 k]）为数据点Pi到聚类mkk重心Ckk的距离（或者说Pi与mkk重心Ckk的差别）。由于所有参与计算的数据都已经进行了标准化转换，所以这里采用欧式距离来计算disi，kk：

2）使用disi，kk的倒数构造一个变量wi，kk，以指出数据点Pi隶属于聚类mkk的隶属度权重。

如果∀disi，kk（kk∈[1 k]）≠0，则：

这里，numkk是聚类mkk所包含的数据点数。

如果∃disi，j（j∈[1 k]）=0，则：

3）构造混合分布矩阵H。使数据点Pi相对于聚类mkk的隶属度权重作为计算隶属度的权重wi∈P，kk∈M，则Hi，kk最终被定义为：

2.3对任意数量指定聚类混合区的定义

设T= {t1，…，tv}（ti-mj=Ø，1< v≤k）为我们所关注的聚类的集合，其是全部聚类集合m的部分或全部。为了定义这些聚类的混合区，首先设集合Rm，n与集合Sm，n是T中任意两个聚类tm与tn（其中m≠n）在相空间上一个交集范围的最大限度：

这里，Zm，n包括了聚类tm和tn所有位于混合区的的数据点的集合，如图3所示。

图3　谱混合模型在v=2，α=0.5，β=0.8，num1 = num2情况下，变量和集合之间相互关系差异的分布结构图

为了方便地将这一概念在任意多个聚类参与的情况下进行描述，现定义∩（ai）：=a1∩a2…∩a1。设Z为位于聚类集合T中所有聚类混合区域的数据点集，则最终Z可以表示为：

这里值得指出的是，谱混合模型在水团分析和锋面分析中具有潜在的以及非常深远的应用前景。在此基础上，定义出两个水团的信息过渡区，并且求解所有信息过渡区的交集。此外，该方法还可用来定义任意多个水团之间的信息过渡区。图4即是一个将集合数目扩大到3个而求解其信息过渡区的实例，实例中，v=3，α=0.5，β=1.0。图中黑色粗线包裹的区域限定了三个聚类a，b和c混合区的最大界限。其中每个聚类所包含的数据点的数量已在各图中各聚类名称后面的括号中给出。

综上，谱混合模型是在谱聚类方法的基础上，通过构建概率密度函数得到每个数据点隶属于某个聚类的隶属度权重，然后引入参数α和β，创造任意两个聚类最大限度的交集集合R和S，从而最终确定混合区（在水交换研究中即水交换区）数据点的集合为。其中参数α和β决定了混合区的空间位置和范围，其中α表示数据点隶属于不同聚类权重的差值，越大说明该数据点越偏离某一聚类；β则用于排除两水团的外边缘区域带来的误差。

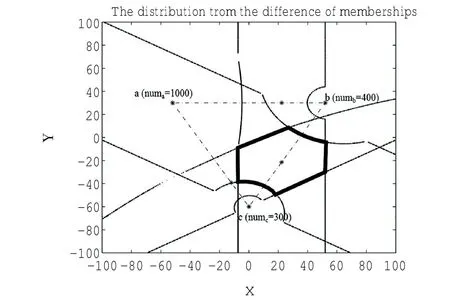
图4　谱混合模型在v=3，α=0.5，β=1.0情况下，变量和集合之间相互关系差异的分布结构图

2.4参数α和β的优化

谱混合模型中的参数α和β，能够保证将不同聚类之间的混合区域限制在各聚类中心连线的中点附近，对混合区的确定起到了关键性的作用，所以找到一种可以优化两参数的方法是十分有必要的。本文对此提出了一套能够优化这两个关键参数的一般方案，具体阐述如下：

若要研究的是混合区的时空变化情况，则在满足混合区域被控制在各聚类之间的前提下，其变化越显著，越有利于研究的进行。为了方便叙述，这里以某一事件的发生，能够引起混合区的变化为例，对优化参数的方法步骤进行阐明。首先定义4个指数IRB、IRA、RA以及TR，其中IRB为事件发生时相对于事件发生前混合区的变化率；IRA为事件发生时相对于事件发生后混合区的变化率；RA为平均气候状态下混合区占总区域的比例；TR则是以上3个指数的总和。

图5显示了在不同参数的配置下，在一个案例中，4个指数的变化分布情况。

首先判断该事件的发生对混合区的影响是加强还是减弱。若有加强作用，则IRB、IRA、RA以及TR 4个指数必须均为正数；反之，指数IRB和IRA为负值；然后，考虑到参数α表示数据点隶属于不同聚类权重的差值，其值越小，所确定的混合区越趋向各聚类中心连线的中点；最后，考虑到混合区的显著性体现，即在满足混合区被控制在各聚类之间的前提下，其占据总区域的比例越大，且在事件前后的变化越明显，越有利于研究的进行。

基于以上3个原则，结合图5中a、b、c、d4张图，最终可以确定该案例中的最佳参数配置为α=0.15，β=0.25。

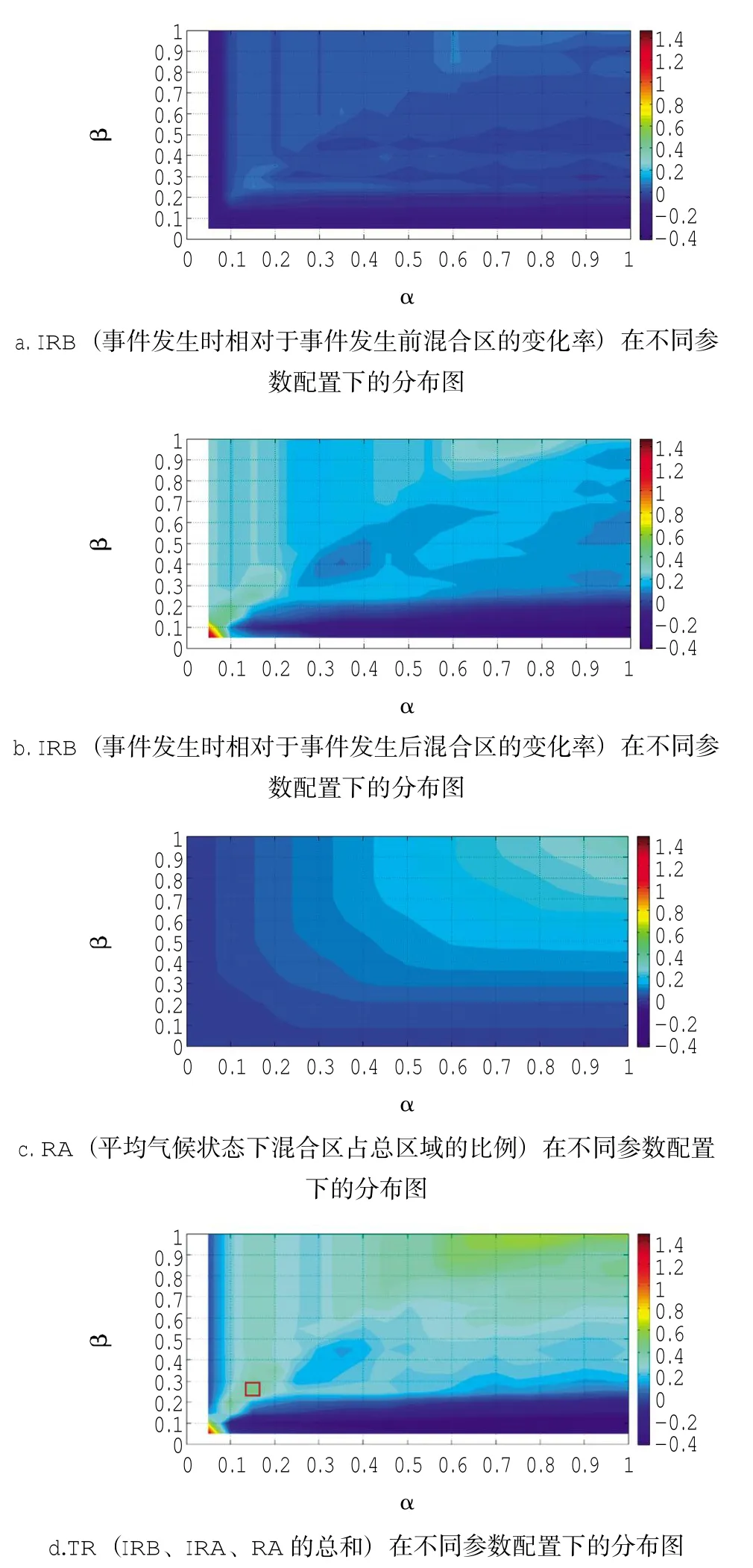
图5　指数IRB、IRA、RA以及TR在不同参数配置下的分布图

此外，若只研究各聚类之间混合区的空间分布情况，而不考虑其随时间的变化，则上述方法中的4个指数只有RA有效，而RA反映的是参数α和β的取值越大，混合区占总区域的面积越大，这显然不能以此确定两个参数的取值，因为该混合区还需要满足位于各聚类之间这一前提条件。故针对这类案例，该参数优化方法并不适用，而是要根据案例的实际情况来对这两个参数进行优化。

3讨论

完善后的谱混合模型能够快速有效地分析水团以及确定水团之间的交换区，但模型中有几点还有必要做进一步得改进。本研究中简单的使用聚类mkk所包含的数据点的数量numkk来表示mkk的势力范围，这个定义是基于所有聚类中数据点的分布密度都是一致的这一前提假设。因此，在对各聚类的数据点分布密度差异较大的情况研究中，建议使用unmkk/ddkk来代替公式（8）中的numkk，这里ddkk表示聚类mkk数据点的平均分布密度。此外，与大多数聚类分析研究一样，聚类个数k在本研究中是给定的。实际上，在更一般的应用当中，最优化的k值可以通过分析求解矩阵L（方程5）得到的特征值序列而得到。一个基本的想法是将这些特征值从小到大排列起来，然后自动确定数目k，使前k个特征值的和相对于所有特征值的和的比例小于某一标准。

参考文献

Andrew Y N，Michael I J，Yair W，2002.On spectral clustering：Analysis and an algorithm.Advances in Neural Information Processing Systems，14（1-2）：849-856.

JitendraM，SB，TL，etal，2001.Contourand textureanalysis for image segmentation.Int JComput，43（1）：7-27.

Lai J，Huang T J，Liaw Y C，2009.A fast k-means clustering algorithm using cluster center displacement.Pattern Recogn，42（11）：2551-2556.

Li F，Jun X，Yao L，2004.New methods of fitting the membership function of oceanic water masses.Journal of Ocean University of China（English Edition），3（1）：1-9.

Luo B，W ilson R C，Hancock E R，2003.Spectral clustering of graphs.Computer Analysis of Images and Patterns，Proceedings，2756：540-548.

Menschaert G，Vandekerckhove T T M，Landuyt B，et al.，2009.Spectral clustering in peptidomics studies helps to unravel modification profile of biologically active peptides and enhances peptide identification rate.Proteomics，9（18）：4381-4388.

Miller A R，1950.A study of mixing processes over the edge of the continentalshelf.J.Mar.Res.，9（2）：145-160.

Shi J，Malik J，2000.The 20th anniversary of the IEEE transactions on pattern analysis and machine intelligence.Ieee T Pattern Anal，22 （1）：1-3.

Song J，Xue H J，Bao X W，W U Dexing etal.，2011.A spectralmixture model analysis of the Kuroshiovariability andthe water exchange between the Kuroshioand the East China Sea.China Journal of Oceanology andLimnology，29（2）：446-459.

Su Y，Yu Z，Li F，1989.The application of the cluster analysis on the shallow water mass analysis.Periodical of Ocean University of China，15（3）：24-28.

Sverdrup H U，Johnson M W，Fleming R H，1942.The oceans，their physics，chemistry and general biology.New York：Pretince-Hall，1-1087.

Von L U，2007.A tutorial on spectral clustering.Stat.Comput，17（4）：395-416.

浦泳修，1981.关于东海北部表层的水系和环流.海洋通报，（5）：10-16

宋军.水交换模型的理论方法及应用研究：（博士学位论文）.青岛：中国海洋大学，2010.

张绪东，张国友，佟凯，等，2004.黑潮源区海域水团分析.海洋通报，23（1）：15-21.

（本文编辑：岳心阳）

Optim ization of the spectralm ixturem odelm ethod and its app lication in theanalysisofwaterm assand water exchange

SONG Jun1，4,LIU Yu-Long1,LIJing1，2,GUO Jun-Ru3,6,MU Lin1,YAO Zhi-Gang4,LIXi-Bin5
（1.NationalMarineDataand Information Service,Tianjin 300171,China;2.CollegeofMarine Science,ShanghaiOcean University,Shanghai201306,China;3.NationalMarineHazard Mitigation Service,SOA,Beijing100194,China;4.MinistryofEducation Key LaboratoryofPhysicalOceanography,Ocean UniversityofChina,Qingdao266100,China;5.Tianjin Marine EnvironmentalMonitoring CentralStation,SOA,TianjinMarine EnvironmentalMonitoringand ForecastingCenter,Tianjin 300451,China;6.Key LaboratoryofSpace Ocean Remote Sensingand Application,Beijing100081,China）

Abstract：The method of spectralmixture model is optimized by determining its two parameters in a better way.The optimized method can make rapidclustering analysis of a large number of data samples.By solving the probability density function，itcan determine themixing areabetween differentclusters.W ith the application of themethod in the ocean water mass and water exchange as an example，this paper illuminates the working principle and process of spectralmixture modelin detail.The analysismethod ofspectralmixturemodelwhich isbased on the spectral clusteringmethod，avoids the inadequacy of thetraditional fuzzy clustering analysis.Even if thescattered data distribution ofphysicalquantity presents a wide range of continuity，it is still able to seize the main changedirectionof the time and space distribution of the data.Hence，ithasawide rangeofapplications in termsof the discrimination ofwatermass，the distribution and change rulesof watermassboundary and themixed areaofwaterexchange.

Keywords：SpectralClustering;SpectralMixtureModel;watermassanalysis;waterexchange;FuzzyMathematics;T-S diagram

通讯作者：郭俊如，博士，电子邮箱：874623647@qq.com。

作者简介：宋军（1983-），男，博士，主要从事近海动力学、业务化海洋学方面的研究。

基金项目：国家自然科学基金（41206013；41376014；41430963；41206004）；教育部物理海洋重点实验室开放基金；2011年度高等学校博士学科点专项科研基金（20110132130001）；海洋公益性行业科研专项（201205018；201005019）；国家科技支撑计划（2014BAB12B02）；天津市科技支撑计划（14ZCZDSF00012）；国家海洋局青年科学基金重点项目（2012202；2013203；2012223）；国家建设高水平大学公派研究生项目（留金出[2008]3019;[2012]3013）；国家海洋向空间遥感与应用研究重点实验室开放基金重点课题（201601003）。

收稿日期：2015-06-10；

修订日期：2015-07-03

Doi：10.11840/j.issn.1001-6392.2016.01.010

中图分类号：P733

文献标识码：A

文章编号：1001-6932（2016）01-0074-07