未反应JBO-9021炸药冲击雨贡纽曲线的研究*
张 涛,赵继波,伍 星,谷 岩,刘高旻
(1.中国工程物理研究院流体物理研究所,四川绵阳 621999;2.中国工程物理研究院总体工程研究所,四川绵阳 621999)
1 引 言
在冲击波作用下未反应炸药的雨贡纽曲线和状态方程是表征炸药性能的关键参数,也是反导战斗部和炸药安全性研究的重要课题之一,对研究炸药的冲击起爆过程、确定化学反应率函数及反应产物状态方程、理解爆轰反应区结构等具有重要意义[1-2]。三氨基三硝基苯(TATB)是常用的钝感高能炸药,TATB和TATB基炸药的爆轰性能(特别是冲击动力学性能)受到国内外研究者的关注[3-4]。南佛罗里达大学的Budzevich等人[5]采用第一性原理计算获得了压力为0~25 GPa时不同晶向TATB晶体的状态方程。Dick等人[6]对冲击作用下TATB基炸药PBX9502的冲击雨贡纽曲线和动态失效模式进行了实验研究,采用轻气炮和化爆加载相结合的方式,同时测量波后粒子速度和冲击波速度,获得了0.5~25.0 GPa压力条件下PBX9502的冲击雨贡纽曲线。Shaw等人[7]采用蒙特卡罗方法对HMX基和TATB基炸药进行仿真模拟,通过修正的内部反应机制,从原子层面获得了未反应PBX9501和PBX9502炸药及爆轰反应产物的状态方程。Gump等人[8]采用金刚石压砧研究了压力为0~6 GPa时未反应LLM-105炸药(与TATB炸药类似)的状态方程。另外,Bourasseau等[9]、Davis[10]、Millett等[11]和Bernecker[12]也对包括TATB在内的多种未反应炸药的雨贡纽曲线和状态方程开展了研究。
目前,在钝感炸药冲击雨贡纽曲线和状态方程研究方面,主要的实验方法是通过多发实验,在不同冲击压力下,测量波后粒子速度或炸药的体积变化,进而根据实验数据拟合得到炸药的冲击雨贡纽曲线和状态方程。然而,该方法的实验成本较高,而且实验数据的精度不高。本研究以新型高能钝感炸药JBO-9021(TATB作为主装药)为研究对象,通过新的实验方法——激光干涉测速技术,对同一发实验中JBO-9021炸药在不同冲击波位置处未反应炸药的冲击雨贡纽曲线进行实验研究,得出在冲击压力为11~21 GPa时JBO-9021炸药的冲击雨贡纽曲线,并将未反应JBO-9021炸药的雨贡纽关系与冲击波阵面的Rankine-Hugoniot关系进行联立,得到未反应炸药在所研究压力范围内的状态方程。
2 实验装置及测试系统
如图1所示,实验装置由起爆装置和测试系统组成。其中测试系统主要包括同步机、高压脉冲发生器、光纤探针、光纤放大器、激光器、激光干涉仪、示波器、计算机控制系统等部分。测试窗口LiF晶体靠近受试炸药的一面镀有铝膜,可以作为粒子速度的载体。为保证测试精度,膜层不宜过厚,实验中铝膜厚度为1.0 μm。另外,为避免输入激光在LiF窗口上表面(靠近光纤探针侧)的反射光影响测试信号光,LiF窗口的上、下表面存在5°的倾角。实验中所用激光干涉测速仪由中国工程物理研究院流体物理研究所研制,其工作原理是基于光学多普勒效应,测速范围为0~8 km/s,测速的不确定度小于2%。

图1 实验装置示意图Fig.1 Schematic diagram of experimental setup
起爆装置外形及内部结构如图2所示。实验中采用∅100 mm平面波透镜作为平面波发生装置,其主装药为RHT-901,主要组成成分为RDX和TNT,质量比为60∶40;采用∅100 mm×10 mm的JO-9159作为传爆药,以HMX为基,HMX与粘结剂的质量比为95∶5;采用∅100 mm×30 mm的JBO-9021作为主装药,以TATB为基,并含有少量HMX;楔形受试炸药也采用JBO-9021,其高度为35 mm,宽度为50 mm,底边长度为60 mm,斜面长度为70 mm,楔形角为30°;钨合金采用∅100 mm×6.08 mm的钨镍铁合金。由于受试炸药为楔形,因此通过一发次实验即可测量得到不同冲击波运动距离后的粒子速度。楔形炸药的侧向尺寸足够大,可以避免边侧稀疏对测量的影响。

图2 起爆装置示意图Fig.2 Photos of detonation system
实验过程中,通过起爆装置向同步机输出起爆信号。同步机输出两路同步信号:一路触发高压脉冲发生器,起爆26号雷管;另一路触发示波器。26号雷管起爆平面波透镜产生平面冲击波,平面冲击波起爆传爆药继而起爆JBO-9021主装药,主装药与钨合金衰减层紧密接触,冲击波经过钨合金衰减层衰减后,进入并起爆JBO-9021楔形受试炸药,驱动紧贴在其表面的铝膜运动;光纤探针将测试激光透过LiF窗口输出至铝膜表面,反射带着楔形炸药块/窗口界面粒子速度信息的多普勒光学信号返回探头,通过光纤放大器进入激光干涉仪,经由光电传感器将承载速度信息的光信号转换成电信号,最后由示波器记录。通过激光干涉测速处理得到楔形炸药块/窗口界面粒子速度剖面。
获得雨贡纽曲线的基本思路是:采用激光干涉测速技术获得受试炸药波后粒子速度剖面,通过不同位置的探针间距和粒子速度起跳时间差获得两探针之间的平均冲击波速度,然后利用曲线拟合得到未反应JBO-9021炸药的雨贡纽曲线。
3 实验结果及分析

图3 受试炸药/LiF窗口界面波后粒子速度曲线Fig.3 Interface velocity-time curves of JBO-9021 explosive/LiF window after shock
实验过程中,冲击波到达钨合金衰减层与受试炸药界面后,进入受试炸药中的冲击波会产生反射波,如果未反应炸药的波阻抗高于钨合金,反射波为冲击波,反之则是稀疏波。在楔形JBO-9021炸药和LiF窗口界面不同位置处安装了光纤探针。光纤探针按照触发的先后顺序依次编号,分别用于测量冲击波进入炸药4、5、6、7、8、9、10、11 mm处时的波后粒子速度,结果如图3所示。
由图2中的实验装置可以看出,采用激光干涉测速技术获取的实际上是楔形JBO-9021炸药/LiF窗口界面粒子速度在垂直于斜面方向的分速度。另外,由于LiF窗口与JBO-9021炸药的阻抗并不完全匹配,测量所得粒子速度并不是受试炸药中稳定爆轰时的波后粒子速度,并且窗口材料在冲击压缩过程中会因折射率发生变化而引起一定的测试误差,因此,需要对探针直接测量得到的波后粒子速度进行修正。
首先,对探针所测得的JBO-9021炸药/LiF窗口界面粒子速度进行角度修正
(1)
式中:v*(t)为样品/窗口界面的“表观”粒子速度,vc(t)为实验测得的在垂直于斜面方向的分速度。
Jensen等人[13]提出在加窗光子多普勒测速中,因冲击压缩作用,窗口折射率的变化会引起附加的多普勒频移,导致测得的界面速度变大。该效应引起的修正为
(2)
式中:a(λ)是窗口修正系数;v*(t)为“表观”粒子速度,即未经过折射率变化修正的速度;v(t)为样品/窗口界面的实际粒子速度;vs(t)是窗口材料自由面的粒子速度。
根据文献[14]对(2)式进行简化,可得样品/窗口界面的实际粒子速度为
JBO-9021炸药是一种新型高能钝感炸药,当前对该炸药的研究还不全面,无法获取其爆轰产物的状态方程。但是,由于PBXC10和JBO-9021炸药均以TATB为基,成分相似,因此可以采用PBXC10的JWL状态方程[15]与冲击波阵面的Rankine-Hugoniot关系进行联立
式中:p为冲击波(爆轰波)波阵面压力,ρ0为炸药的初始密度,ρ为冲击波后JBO-9021炸药的密度,Ds为冲击波速度,up为冲击波后的粒子速度。
计算得到JBO-9021炸药的雨贡纽关系为
(7)
单晶LiF窗口的雨贡纽曲线为[16]
(8)

图4 修正后受试炸药的波后粒子速度Fig.4 Velocity-time curves of JBO-9021 explosive after correction
根据界面连续定理,在接触界面上,冲击波后的压力和粒子速度不能出现间断。同时,将冲击波阵面的动量守恒定理((5)式)代入,对受试炸药/LiF窗口界面粒子速度曲线进行二次修正,得出冲击波进入受试炸药不同位置处修正后的波后粒子速度up,如图4所示,具体数值见表1。


表1 探针测量所得JBO-9021炸药不同位置处的波后粒子速度Table 1 Particle velocities after shock at different positions of JBO-9021 explosive
由于本方法使用的冲击波速度为相邻两探针之间的平均值,因此,为得到与之对应的粒子速度,需要对粒子速度进行曲线拟合,通过积分求平均的方法获取up在相应距离间的平均值。
采用指数函数对不同位置处探针测得的冲击波后粒子速度进行拟合,所得拟合曲线如图5所示,即粒子速度与冲击波进入炸药距离的关系为
(9)
式中:x为冲击波进入受试炸药的距离,up为该处的波后粒子速度。
通过积分的方法可以得到粒子速度在4~5 mm、5~6 mm、6~7 mm、7~8 mm内的平均值,即
(10)

根据图4中冲击波波后粒子速度剖面可以获得相邻探针粒子速度的起跳时间差,由此计算得到相邻探针之间冲击波速度的平均值
(11)
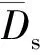

(12)
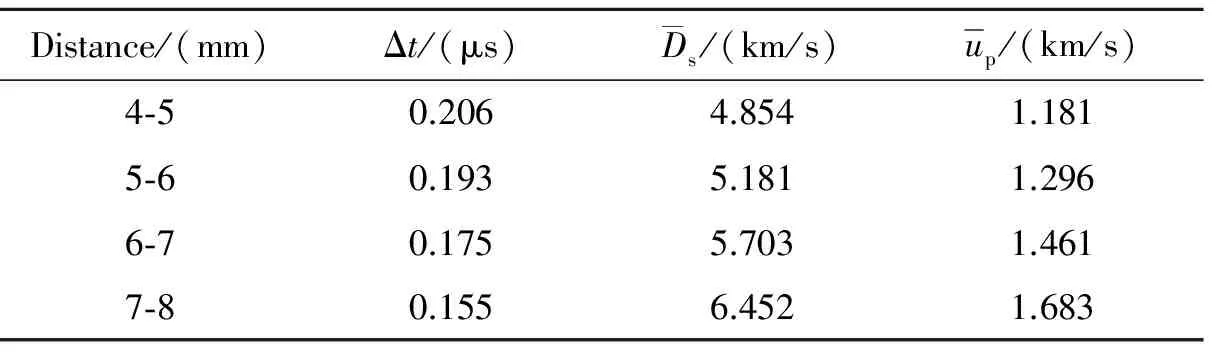
表2 相邻探针之间冲击波速度和粒子速度的平均值Table 2 Average velocities of shock wave and particle between adjacent probes

图5 受试炸药波后粒子速度随距离的变化Fig.5 Velocity-position curve of JBO-9021 explosive

图6 未反应JBO-9021炸药的冲击雨贡纽关系Fig.6 Hugoniot curve of unreacted JBO-9021 explosive

(13)
(13)式中的状态方程形式简洁,适用的压力范围为11~21 GPa。
4 结 论
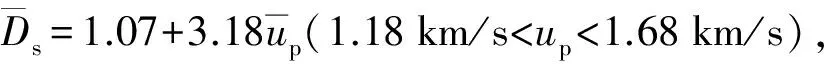
[1] BOUYER V,DOUCET M,DECARIS L.Experimental measurements of the detonation wave profile in a TATB based explosive [J].EPJ Web of Conferences,2010,10:00030.
[2] BOUYER V,HEBERT P,DOUCET M,et al.Experimental measurements of the chemical reaction zone of TATB and HMX based explosives [C]//APS Shock Compression of Condensed Matter.Maryland:American Physical Society,2011.
[3] 黄奎邦,陈永丽,于 鑫,等.JB-9014炸药的化学反应率参数及应用研究 [J].爆炸与冲击,2013,33(增刊):140-144.
HUANG K B,CHEN Y L,YU X,et al.Parameters and application research of reaction rate for JB-9014 explosive [J].Explosion and Shock Waves,2013,33(Suppl):140-144.
[4] GUSTAVSEN R L,THOMPSON D G,OLINGER B W,et al.Shock initiation experiments on ratchet grown PBX 9502 [C]//14th Symposium on Detonation.Los Alamos:Los Alamos National Laboratory,2010:698-703.
[5] BUDZEVICH M,CONROY M,LANDERVILLE A,et al.Hydrostatic equation of state and anisotropic constitutive relationships in 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) [C]//Proceedings of the American Physical Society Topical Group on Shock Compression of Condensed Matter.New York:American Institute of Physics,2009,1195(1):545-548.
[6] DICK J J,FOREST C A,RAMSEY J B,et al.The Hugoniot and shock sensitivity of a plastic-bonded TATB explosive PBX 9502 [J].J Appl Phys,1988,63(10):4881-4888.
[7] SHAW M S.Direct simulation of detonation products equation of state by a composite monte carlo method [C]//12th Symposium on Detonation.Los Alamos:Los Alamos National Laboratory,2002:913-922.
[8] GUMP J C,STOLTZ C A,MASON B P.Unreacted equations of state of LLM-105 and thermal stability of TATB [C]//13th Symposium on Detonation.Los Alamos:Los Alamos National Laboratory,2008:553-559
[9] BOURASSEAU E,MAILLET J B,DESBIENS N,et al.Microscopic calculations of Hugoniot curves of neat triaminotrinitrobenzene (TATB) and of its detonation products [J].J Phys Chem A,2011,115(39):10729-10737.
[10] DAVIS W C.Complete equation of state for unreacted solid explosive [J].Combust Flame,2000,120(3):399-403.
[11] MILLETT J,BOURNE N,ROSENBERG Z.Observations of the Hugoniot curves for glasses as measured by embedded stress gauges [J].J Appl Phys,1998,84(2):739-741.
[12] BERNECKER R R.Observations on the Hugoniot for HMX [C]//Proceedings of the American Physical Society Topical Group on Shock Compression of Condensed Matter.New York:American Institute of Physics,1996,370(1):141-144.
[13] JENSEN B J,HOLTKAMP D B,RIGG P A,et al.Accuracy limits and window corrections for photon Doppler velocimetry [J].J Appl Phys,2007,101(1):013523.
[14] LALONE B M,FAT’YANOV O V,ASAY J R,et al.Velocity correction and refractive index changes for [100] lithium fluoride optical windows under shock compression,recompression,and unloading [J].J Appl Phys,2008,103(9):093505.
[15] MADER C L.Numerical modeling of detonation [M].Berkely:University of California Press,1979.
[16] CARTER W J.Hugoniot equation of state of some alkali halides [J].High Temp High Press,1973,5:313-318.

