冰区航行船舶碎冰阻力预报数值模拟方法

郭春雨，李夏炎，王帅，赵大刚

(哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001)



冰区航行船舶碎冰阻力预报数值模拟方法

郭春雨，李夏炎，王帅，赵大刚

(哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001)

摘要：随着越来越多的国家认识到北极地区巨大的潜在价值，冰区船舶的性能研究和设计工作也愈发的为人们重视。为了研究冰区船舶在碎冰区域内的航行阻力，运用Ls-dyna软件的罚函数算法和流固耦合算法对冰区船舶在碎冰中航行过程进行了数值模拟，分别计算了60%、80%和90%碎冰密集度下4个速度点的船-冰作用力。在船模拖曳水池非冻结模型冰试验的基础上，对数值模拟结果进行分析评估。认为数值模拟结果在较低速度条件下在定性上与试验结果比较符合，数值模拟方法在冰区船阻力性能研究工作中有着重要的参考价值。

关键词：冰区船；船舶阻力；模型试验；有限元方法；罚函数法；流固耦合

近年来，随着全球气候变暖、资源能源紧缺，蕴藏着巨大潜在价值的北极地区的科考开发工作备受相关国家重视。由此，破冰船、极地科考船、冰区运输船等冰区航行船舶的基础性能研究工作也成为当前的研究热点。目前冰与结构物相互作用的研究领域内的成果主要集中在冰力学性能[1-2]和冰-固定锥形结构[3]相互作用的研究领域，船-冰作用的研究进展有限。而在船-冰作用的研究中，以破冰船和平整冰碰撞作用[4]的情况为主，对冰区航行船舶在碎冰区域内的阻力性能预报研究进行的较少，使用的研究方法通常为理论分析方法或孤立的数值模拟方法，由于条件限制，船模试验往往很少进行。目前，碎冰区域内的冰区航行船舶阻力性能研究尚处于起步阶段，研究成果有限，大量问题需要解决。因此，开展冰区航行船舶在碎冰区域内的阻力性能研究工作具有重要的价值和意义。

在数值模拟方面，国内进行的有限元软件模拟碎冰中船舶阻力的相关研究很少，国际上的研究也处于起步阶段。Jung-Yong Wang等[5]使用LS-DYNA软件对加拿大Terry Fox号标准破冰船模型在60%碎冰密集度条件下两种碎冰厚度(20 mm、40 mm)下的两个速度点(0.4 m/s、0.6 m/s)的碎冰阻力进行了模拟，并与试验结果进行了对比，模拟结果误差值在100%～600%，结论认为数值模拟在高速度点的模拟结果并没有真实反映实际船-冰作用情况，在低速度点的结果尚可以接受。Sang-Gab Lee[6]等使用LS-DYNA模拟了2艘不同船艏的冰区货船模型在预切割冰的数值冰槽中的碎冰阻力，模拟的船舶航速为0.483 m/s。两艘船的数值模拟的结果均高于试验值，其中船型1的结果误差为9%，船型2的误差为18%。Moon-Chan Kim等[7]使用LS-DYNA软件对一艘冰区货船模型进行了统一碎冰尺寸下的3种碎冰密集度(60%、80%和90%)，3个速度点(0.1、0.3和0.6 m/s)的碎冰阻力进行了模拟。并将数值模拟结果同时与冻结模型冰试验和非冻结模型冰试验进行对比，结果误差值在10%～150%。Moon-Chan Kim 全面深入的分析对比了LS-DYNA软件的模拟结果与试验结果的差异，具有重要参考价值。文章结论认为数值模拟结果在定性和定量上均与试验结果保持了一致性，数值模拟方法能够在冰区船船型优化研究中发挥作用。

本文在国外学者研究工作的基础上，使用数值模拟方法研究冰区船碎冰阻力，通过ANSYS软件进行模型建立、设定边界条件等前处理工作，使用LS-DYNA软件进行求解计算，使用LS-PREPOST软件进行后处理分析，完成对碎冰区域内冰区船舶航行过程的数值模拟，计算船-冰作用力。同时对比拖曳水池实验室进行的非冻结模型冰船模试验结果，旨在对使用LS-DYNA软件进行数值模拟计算的方法进行初探，评估数值模拟方法的价值和可靠性。

1碎冰阻力数值模拟预报方法

冰区航行船舶阻力预报方法主要有：理论方法、数值模拟方法和试验方法，其中试验方法是研究冰区船船舶性能的最直接和全面的方法。然而，无论是实船试验还是船模试验，都受到试验条件和测试技术的约束，并不能够广泛、便捷地应用在研究当中。同时，对理论方法而言，无论是理论模型分析还是经验公式方法，都建立在大量假定条件和近似情况的基础上，适用范围有限。而与试验方法和理论方法相比，数值模拟方法可以对冰区船舶在碎冰区域航行这一过程进行快捷、准确地全过程模拟，得到不同时刻的物理图像和瞬时数据，有着很高的研究价值[8]。

本文使用 ANSYS/LS-DYNA 非线性显示动力学分析软件，模拟KCS船在60%、80%、90%冰密度的碎冰区域内的航行过程，分析船-冰相互作用力的变化，同时与哈尔滨工程大学拖曳水池非冻结模型冰试验结果进行对比。

1.1数值模拟的理论准备

冰区航行船舶在碎冰区域航行的过程，主要包括两个相互作用关系，即：船-冰碰撞作用和流(水、空气)-固(船、冰)耦合作用。在模拟时，应当对这两种相互作用关系的计算方法分别进行考虑。

1.1.1船-冰碰撞的接触算法

LS-DYNA 程序中，并没有其他隐式有限元分析程序中常用的接触单元，无法通过接触单元模拟接触。而是需要定义可能的接触表面和接触类型，并设定与接触有关的参数，这样程序就能较精确地模拟运动物体的相互作用，保证接触面之间不发生穿透并能够考虑摩擦力的作用。LS-DYNA 的全自动接触分析功能使用非常方便，有 50 多种可供使用的接触分析方法，可以求解不同类型的柔性体与柔性体、柔性体与刚性体、刚性体与刚性体之间的接触问题，并可考虑接触表面的静动力摩擦系数、固连失效问题以及流体与固体的交界面等。

本例中将使用罚函数法对船与冰的碰撞问题进行计算。罚函数法的原理是：每一时间步首先检查各个从节点是否对主面发生穿透现象，如果没有发生穿透现象，跳过该从节点；如果发生穿透现象，则在这个从节点与发生穿透的主表面之间引入一个较大的界面接触力，界面接触力的大小和穿透深度、接触面刚度成正比，称为做罚函数值。罚函数法的物理意义类似于在其中放置一系列法向弹簧，以限制穿透作用[9]。

罚函数算法的计算原理简单，守恒准确，容易进行编程，不容易引起沙漏效应，没有噪声，不需要设定碰撞和释放条件，在LS-DYNA获得广泛应用，为该软件的缺省算法。

1.1.2流固耦合算法

本例中采用ALE算法处理冰区船在碎冰区域航行的流固耦合问题的计算。ALE (arbitrary Lagrangian-Eulerian)算法在结构边界运动的处理上，能够有效地跟踪物质结构边界的运动；在内部网格的划分上，独立于物质实体的存在，使得网格不致出现严重的畸变。ALE方法可以处理整个物体在空间的大位移且本身有大变形的问题。

计算中，ALE 算法先执行一个或几个 Lagrange 时步计算，此时单元网格随材料流动而产生变形，然后执行 ALE 时步计算：

1)保持变形后的物体边界条件，对内部单元进行重分网格，网格的拓扑关系保持不变，称为 smooth step；

2)将变形网格中的单元变量(密度、能量、应力张量等)和节点速度矢量输运到重分后的新网格中，称为 advection step。

这样就完成了ALE算法的一步计算[10]。

1.2数值模拟的计算流程

不管是试验设计、还是进行数值模拟，都需要满足一定的相似条件，才能够有着实际的科研和工程意义。由于本次试验和模拟都是设定在碎冰条件下，基本上不存在破冰情况，重力、惯性力和摩擦力占主导作用，与一般船模水池试验中的相关力相同，因此需要满足的相似准数为傅汝德数、雷诺数、柯西数。在此相似准则的基础上设计了冰区航行船舶在非冻结模型冰中的船模试验。为了与试验结果进行对比，数值模拟的条件设定与试验条件相同。

1.2.1 前处理

使用ANSYS进行前处理，包括定义单元类型和材料属性、数值建模、划分网格、定义PART和接触等。其中数值建模的主体包括四个部分：船、空气、水、冰。为了与试验保持一致，同时降低计算成本，本次模拟把船模材料设置为刚体，同时忽略了冰的破碎作用，仅考虑船-冰之间的挤压、碰撞、推移作用。主要建模的单元和材料属性如表1所示。

表1　数值模拟的主要建模参数

1)船

船体模型为KCS船模型，为了方便与试验进行对照，建立模型尺寸与试验选用船模保持一致，如图1所示，具体参数如表2如所示。

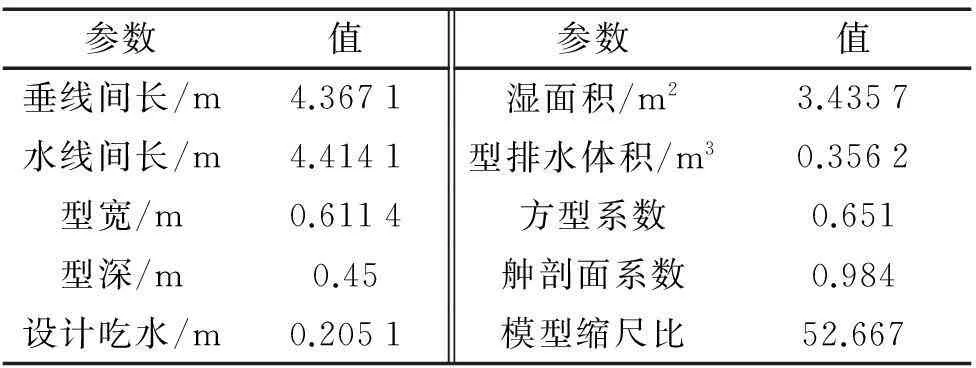
表2　船模的主要参数

图1　船模和网格示意图Fig.1　Sketch of ship model and grid

2)流体域

流体域包括空气域和水域两个区域，其中空气域的模型尺寸为10 m×3 m×0.3 m，水域的模型尺寸为10 m×3 m×0.6 m。空气的状态方程为*Eos_Linear_ Polynomial，水的状态方程为*Eos_Gruneisen。网格划分使用边长为0.1 m的体网格，对主要与冰作用的上层水域进行网格加密。流体域模型及网格如图2所示。

图2　流体域模型和网格示意图Fig.2　Sketch of fluid domain and grid

3)碎冰

根据北极碎冰尺寸统计数据，碎冰形状通常为多边形，尺寸的数量服从对数正态分布函数。因此，模拟采用了6种不同尺寸的模型(厚度均为2 cm)，在流体域中混合分布，碎冰的密度根据需要分别为60%、80%和90%。以60%碎冰密度为例，使用的碎冰尺寸及数量如表3所示。

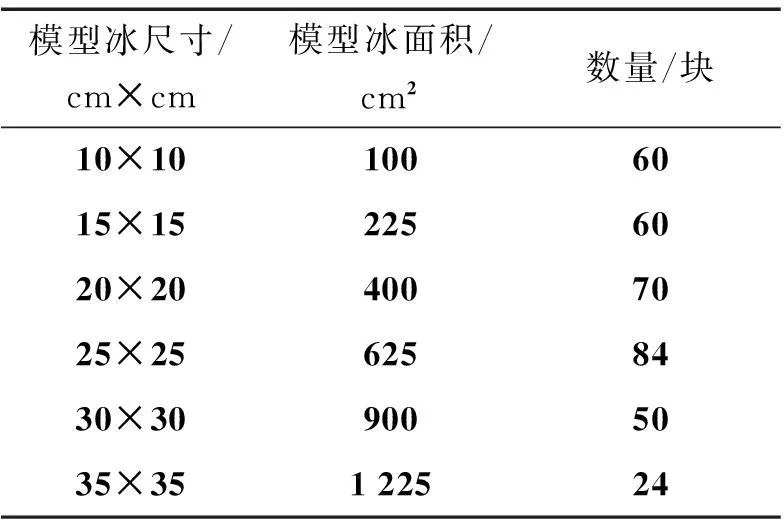
表3　碎冰尺寸

60%碎冰密集度下碎冰模型如图3所示。全部的计算模型如图4所示(空气域未显示)。

图3　碎冰模型示意图Fig.3　Sketch of crushed ice

图4　整体模型示意图Fig.4　Sketch of overall model

建立模型、划分网格完成后，需要对模型进行载荷、约束、碰撞和边界条件的设定。由于模拟航速主要集中在低速度点，同时试验中围栏和碎冰都减少了兴波作用和池壁效应对碎冰阻力的影响，因此模拟中仍然将水的边界设置为无反射边界。船与冰、冰与冰之间使用自动面面接触，给船添加x方向的速度载荷，约束船在y、z方向上的位移，给冰添加重力加速度载荷，约束冰的边界使其不脱离流体域。这样就补充完成了模型的各项条件设定。

1.2.2LS-DYNA计算

在使用ANSYS进行前处理建模之后，紧接着进行求解设置，包括设定计算时间、输出间隔、保存数据类型等等。设定完成后输出K文件，导入LS-DYNA软件对模型进行计算。LS-DYNA有一部分的功能并不能直接通过ANSYS设置直接生成在K文件中，尤其是关于流固耦合部分的参数设定，因此需要在输出K文件后进行手动添加和修改。

本例中数值模拟需要修改的K文件内容主要包括：

1)将流体域的材料单元算法由*SECTION _SOLID更改为*SECTION_SOLID_ALE，并添加流体域的材料定义命令：*MAT_NULL、*EOS_ GRUNEISEN和*EOS_LINEAR_POLYNOMIAL；

2)添流固耦合的相关定义命令，包括：*CONTROL_ALE，*ALE_MULTI-MATERIAL_GROUP，*SET_PART_LIST，*CONSTRAINED_LAGRANGE_IN_SOLID。

完成修改并检查无误后即可以进行计算。

2结果分析

由于冰区航行船舶在碎冰区域内的航速较低，为了更好的和实际情况结合，本次模拟选取了3种不同密集度碎冰下的4个较低的速度点，分别为：0.2、0.4、0.6、0.8 m/s。为了更全面的评估数值模拟的结果，将船模水池试验室进行的冰区航行船舶非冻结冰模型试验与数值模拟计算的结果进行对比。

2.1船模试验

冰区航行船舶非冻结冰模型试验在哈尔滨工程大学拖曳水池中进行，船模拖曳水池的尺寸为：长×宽×深分别为108 m×7 m×3.5 m，非冻结模型冰材料为石蜡，密度平均值为0.900 1 g/cm3，由于本次试验中不涉及碎冰的破碎作用，因此无需考虑弹性模量等参数。相似准数为傅汝德数、雷诺数、柯西数等。本次为了减少池壁效应，在水池中围成一个长28 m、宽3 m的碎冰区，如图5所示。

图5　围栏的实际效果图Fig.5　The actual rendering of fence

同时在碎冰区的尽头另设长8 m宽3 m的缓冲区。先在静水条件下进阻力试验，之后在碎冰条件下对应速度点进行船模阻力试验，碎冰区的碎冰密集度有4种，依次是60%、70%、80%和90%密集度，6个速度点分别为：0.2、0.4、0.6、0.8、1.0、1.2 m/s。

试验测量得到的敞水和不同密集度工况下平均总阻力随速度变化曲线见图6所示。

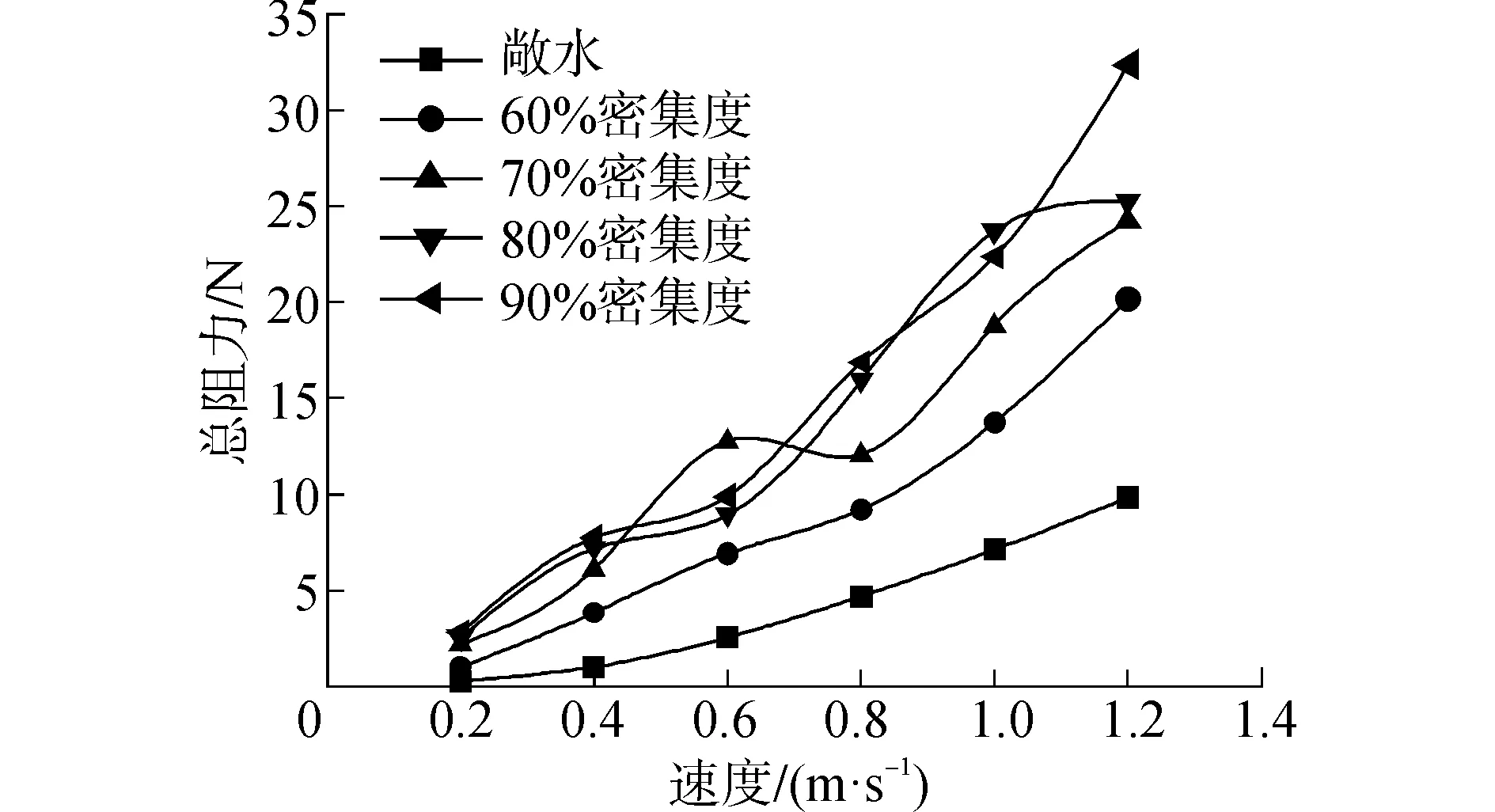
图6　不同工况下总阻力随速度变化曲线Fig.6　The total resistance versus velocity for different conditions

2.2 结果分析和对比

由于本次模拟只是对数值模拟方法的初步尝试和研究，考虑到实际航行情况、使用需求和计算成本，对60%、80%、90%密度下的0.2、0.4、0.6、0.8 m/s等4个速度点进行模拟，并与试验结果对照，主要包括现象对比和数值对比2个方面。

通过LS-PREPOST后处理软件，能够明显地观察到碎冰翻转、碎冰堆积、碎冰滑移等典型物理现象。如图7～9所示。试验表明数值模拟能够充分的反映冰区航行船舶在碎冰区域内的航行现象，与试验取得了良好的一致性。

冰区航行船舶在碎冰区域内的航行阻力成分中，与冰相互作用的阻力成分比重远远大于与水相互作用的阻力成分。相对于敞水阻力的试验和数值模拟技术，冰区船舶的各项研究还在起步探索阶段，尚未成熟。因此本次模拟主要关注最重要的船-冰相互作用力部分，也即冰区航行船舶在碎冰区域内航行时的碎冰阻力，而不在冰区船与水的相互作用部分做进一步研究。

通过LS-PREPOST进行后处理，能够输出船与碎冰碰撞的碰撞力，提取其在x方向上的分量，即为冰区航行船舶在碎冰区域内航行时的碎冰阻力。而在模型试验中，首先进行了敞水试验，测量得到了船模的静水阻力，随后进行了碎冰中的航行试验，测得了碎冰中的航行总阻力。使用碎冰中的航行总阻力值减去静水阻力值，即得到了船与碎冰相互作用的碎冰阻力。

试验结果方面，由于碎冰分布的随机性，冰-船相互作用的偶然性和复杂性，导致冰区船的碎冰阻力结果并不能像敞水试验那样稳定在一个较小的范围内波动。冰块的堆积、翻转、滑移的不确定性对瞬时的力的载荷影响极大，会使碎冰力在短时间内发生较大的波动，难以找到数值上的规律性。而在数值模拟结果方面，由于碎冰的分布不可能与试验完全相同，碎冰阻力的瞬时非定常曲线与试验结果显然不具有数值上的对照性，但是仍然能够反映出冰区船碎冰瞬时阻力变化的随机和震荡，在研究冰区船冰力载荷和船体强度方面有一定意义。以90%碎冰密度、速度为0.4 m/s的情况为例，试验与数值模拟的非定常瞬时碎冰阻力曲线如图10所示。

图7　试验与数值模拟中的碎冰翻转现象Fig.7　Crushed ice inversion in test and numerical simulation

图8　试验与数值模拟中的碎冰堆积现象Fig.8　Crushed ice inversion in test and in numerical simulation

图9　试验与数值模拟中的碎冰滑移现象Fig.9　Crushed ice accumulation in test and numerical simulation

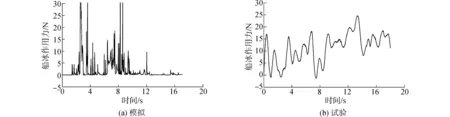
图10　 试验与数值模拟的船冰作用力-时间的非定常曲线图Fig.10　The unsteady force-time curve of test and numerical simulation

同样由于碎冰分布的随机性和试验时船-冰相互作用的不确定性，同一密集度、同一速度点下的两次试验测量得到的阻力平均值会存在比较大的差距，差距甚至有数倍之多。在冰块尺寸更大更密集的区域内，冰块更容易产生堆积，船艏并不能够迅速地将冰块冲散到船两侧，而是顶着堆积的冰块向前行驶，导致阻力平均值增大。而在一次船模试验过程中，冰块堆积效果总是或多或少的出现，不受人为控制。冰块滑移和冰块翻转也同时影响着冰区船阻力测量值的大小。因此，同一密集度和速度点的几次测量值会出现较大的差别，这也是冰区船阻力试验与普通船阻力试验的重要区别。

在冰区，船在碎冰阻力的规律上与普通船的阻力规律也有着很大区别。如试验结果显示：在70%碎冰密集度下，0.6 m/s航速的碎冰阻力大于0.8 m/s时的碎冰阻力；80%碎冰密集度时，1.0 m/s的碎冰阻力大于1.2 m/s的碎冰阻力；在1.0 m/s的航速时，80%碎冰密集度的碎冰阻力大于90%密集度的碎冰阻力。总而言之，碎冰阻力并不像设想的那样，随着速度的增加或碎冰密集度的增加，呈现一个简单的有规律递增的关系。同样在数值模拟的结果中，也出现了类似不规律的变化。由于对冰区船碎冰阻力研究才刚刚起步，在理论上对于以上现象并不能够有一个合理全面的解释。

在此基础上，仅仅是比较数值模拟结果与试验结果数值上的误差，意义并不会很大。目前国际上的数值模拟结果，在某些密集度和速度点条件下误差能够达到30%以内，在某些点的误差多达50%以上，普遍误差在30%～50%之间，即为可以接受的误差。因此在数值模拟结果与试验结果方面对照时，应当主要以线性规律的对比为主，对试验数据和数值模拟数据分别进行线性拟合，对比其随着速度增加，阻力的线性变化趋势。

因为较低的速度更为符合冰区船舶实际的航行条件，从而更加具有研究价值。根据在试验中得到的3种密集度条件下冰区船在0.2、0.4、0.6、0.8 m/s等4个速度点的碎冰阻力试验数据，和数值模拟进行的0.2、0.4、0.6、0.8 m/s等4个速度点的碎冰阻力模拟数据，分别对两种结果得到的数据进行线性拟合。线性拟合结果对比如图11所示。

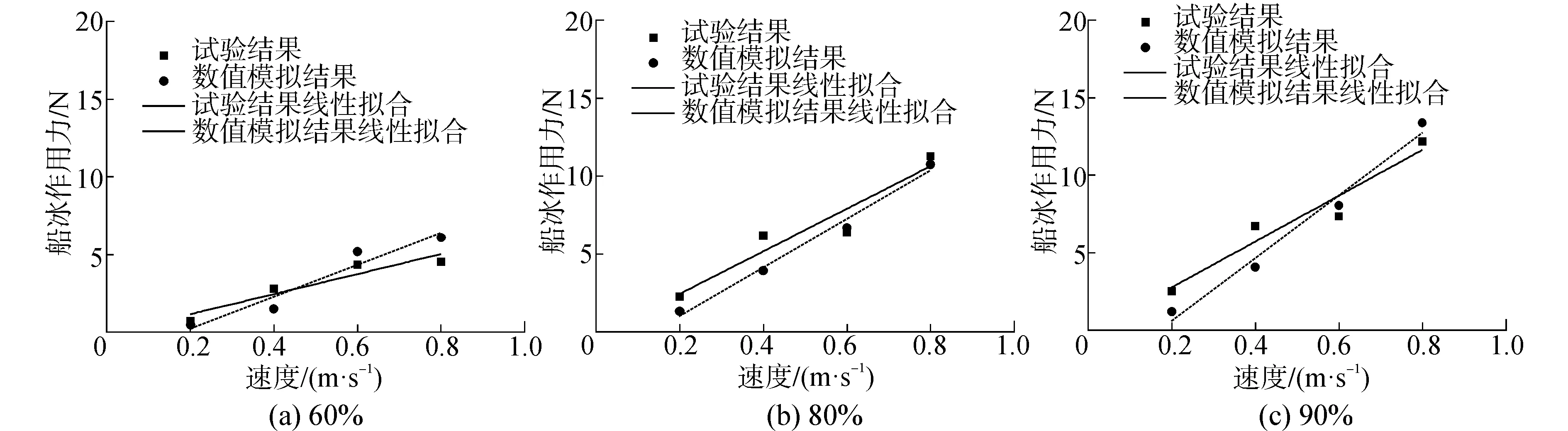
图11　60%、80%、90%密集度下的数值模拟与试验的线性拟合对比图Fig.11　Linear fitting of numerical simulation and test at 60% ，80%，90% concentration ice

三种密集度下的数值模拟结果与试验结果的线性拟合图显示：数值模拟结果在高密集度碎冰条件下要好于低密集度碎冰条件，在高航速条件下的误差好于低航速的误差。在定性上，两种结果的线性趋势有着良好的一致性；在定量上，数值模拟与试验结果的普遍误差在50%以内，根据目前国际上研究的水平，属于可以接受的范围之内。由于目前在冰区船研究领域的数值模拟方法并不能达到普通船的精度，不能够提供准确的数值上的预报，但仍然能良好的反映冰区船碎冰阻力的变化趋势，从而作为冰区船试验的补充。未来的数值模拟方法研究，应当以提高精度，增加计算变量因素为主要研究方向。

3结论

1)使用ANSYS/LS-DYNA软件能够对冰区航行船舶在碎冰区域的航行过程进行模拟，能够很好的反映碎冰翻转、碎冰滑移、碎冰堆积等典型现象。

2)在本次模拟的3种碎冰密集度(60%、80%、90%)，4个较低速度点(0.2、0.4、0.6、0.8 m/s)条件下，碎冰阻力的数值模拟结果在定性上与试验值有着良好的一致性，能够反映试验结果中碎冰阻力随着速度变化的趋势，具有重要的参考价值。这一结论与Moon-Chan Kim等[7]的研究结论基本吻合，数值模拟结果误差与目前国际研究水平一致，其他碎冰密集度和更高速度点的情况仍需要进一步的研究。

3)不管是冻结模型冰试验还是非冻结模型冰试验，通过试验方法研究冰区船舶阻力预报依然受到众多约束，不能广泛的应用在冰区船的研究中。相比之下，数值模拟方法有着很大的优势，能够作为试验方法的补充。

4)本次研究仅仅是对数值模拟方法在冰区船碎冰阻力预报领域的一次应用尝试，仍然有很多不足。未来的工作将着力于进一步提高计算精度，并计算更多影响因素(如碎冰密集度、船速、碎冰尺寸、船型等)下的多种条件的碎冰阻力。

参考文献：

[1]李志军, 王永学. 渤海海冰工程设计特征参数[J]. 海洋工程, 2000, 18(1): 61-64, 69.

LI Zhijun, WANG Yongxue. Design criteria of Bohai Sea ice-control engineering[J]. The ocean engineering, 2000, 18(1): 61-64, 69.

[2]黄焱, 田育丰. 钢管桩防腐护甲的冰磨蚀试验[J]. 天津大学学报：自然科学与工程技术版, 2013, 46(4): 373-379.

HUANG Yan, TIAN Yufeng. Ice abrasion experiments on steel-pipe pile corrosion protection system[J]. Journal of Tianjin university: science and technology, 2013, 46(4): 373-379.

[3]史庆增, 黄焱, 宋安, 等. 锥体冰力的实验研究[J]. 海洋工程, 2004, 22(1): 88-92.

SHI Qingzeng, HUANG Yan, SONG An, et al. Experimental study of ice force on conical structures[J]. The ocean engineering, 2004, 22(1): 88-92.

[4]王钰涵, 李辉, 任慧龙, 等. 连续破冰模式下破冰船的冰力研究[J]. 海洋工程, 2013, 31(4): 68-73.

WNAG Yuhan, LI Hui, REN Huilong, et al. Study of ice force about icebreaker based on continuous breaking pattern[J]. The ocean engineering, 2013, 31(4): 68-73.

[5]WANG J, DERRADJI-AOUAT A. Ship performance in broken ice floes-Preliminary numerical simulations. TR-2010-24[R]. [S.l.]: National research council, 2010.

[6]LEE S G, ZHAO Tuo, KIM G S, et al. Ice resistance test simulation of arctic cargo vessel using FSI analysis technique[C]//Proceedings of the Twenty-third International Offshore and Polar Engineering Conference. Anchorage, Alaska, USA, 2013.

[7]KIM M C, LEE S K, LEE W J, et al. Numerical and experimental investigation of the resistance performance of an ice breaking cargo vessel in pack ice conditions[J]. International journal of naval architecture and ocean engineering, 2013, 5(1): 116-131.

[8]郭春雨, 李夏炎, 谢畅, 等. 冰区航行船舶阻力预报方法[J]. 哈尔滨工程大学学报, 2015, 36(7): 899-905.

GUO Chunyu, LI Xiayan, XIE Chang, et al. Prediction method for icebreaker resistance[J]. Journal of Harbin engineering university, 2015, 36(7): 899-905.

[9]李裕春, 时党勇, 赵远. ANSYS11.0/LS-DYNA基础理论与工程实践[M]. 北京: 中国水利水电出版社, 2008: 63-67.

[10]赵海鸥. LS-DYNA动力分析指南[M]. 北京: 兵器工业出版社, 2003: 149-151.

A numerical simulation method for resistance prediction of ship in pack ice

GUO Chunyu, LI Xiayan, WANG Shuai, ZHAO Dagang

( College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China)

Abstract：As more and more countries have recognized the huge potential value of the arctic, performance research and design work of ship in pack ice are drawing more and more attention of people. In order to study the ship resistance in the crushed ice area, this paper uses the penalty function algorithm and fluid structure interaction algorithm of ls-dyna software to carry out numerical simulation for the sailing process in crushed ice, and calculates the force between ship and ice at four speed points under 60%, 80% and 90% of crushed icedensities. On the basis of non-refrigerated ice model test in ship model towing tank, the results of numerical simulation is analyzed. The results of numerical simulation are in good accordance with the test results on qualitative level at low speeds. Numerical simulation method has important reference value for the research work of ship resistance in ice region.

Keywords：ship in pack ice; ship resistance; model test; finite element method; penalty method; fluid structure interaction

中图分类号：U661.31+1

文献标志码：A

文章编号：1006-7043(2016)02-0145-07

doi:10.11990/jheu.201507064

作者简介：郭春雨(1981-), 男,教授,博士后.通信作者：郭春雨，E-mail: guochunyu_heu@outlook.com.

基金项目：国家自然科学基金资助项目(41176074，51209048)；教育部博士点基金资助项目(20102304120026).

收稿日期：2015-07-21.网络出版日期：2015-12-15.

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20151215.1030.006.html