上硬下软地层盾构隧道开挖面极限支护力分析*1

赵明华，毛　韬，牛浩懿，刘　猛

(湖南大学 岩土工程研究所，湖南 长沙　410082)



上硬下软地层盾构隧道开挖面极限支护力分析*1

赵明华1†，毛韬，牛浩懿，刘猛

(湖南大学 岩土工程研究所，湖南 长沙410082)

摘要：极限支护力是保证盾构隧道开挖面稳定性的关键参数.但目前鲜有学者研究上硬下软地层中盾构隧道开挖面极限支护力的现状．本文基于极限平衡法和筒仓理论，假设破坏面为折线，建立了适用于该地层的盾构隧道开挖面极限支护力计算模型，并得到其计算公式；进而对该地层模型进行数值模拟．结果表明，与不考虑地层分层的传统方法相比较，本文方法与数值计算结果更为吻合，证明了当开挖面横跨上硬下软地层时考虑分层的必要性．在此基础上，对埋深、上下土层厚度及土体强度指标等参数对极限支护力的影响进行了分析．结果表明：当上下地层土质不同时,考虑分层与否所得的极限支护力差异较大.因此，上硬下软地层不能等同于均质土层，在工程实践中需予以考虑.

关键词：盾构隧道；上硬下软地层；极限支护力；筒仓理论；极限平衡；数值模拟

随着我国城市轨道交通的发展，盾构技术得到了广泛应用[1]，同时也成为岩土工程界研究的热点；而极限支护力作为保证盾构开挖面稳定的关键参数，关于其理论计算方法的研究得到了学术界的持续关注[2-13].

目前，对极限支护力的计算方法主要有极限平衡法[2-11]和极限分析法[12-13].

其中极限平衡法，由于其概念明确，计算便捷，易推广，受到工程技术人员的青睐.目前，应用最为广泛的是基于筒仓理论[2]的楔形体模型，假设合理，较之后者计算简易，更为工程技术人员所认可.筒仓理论[2]认为隧道开挖时前方土体由下方滑动体及上方土柱体共同组成.Horn[3]基于筒仓理论[2]提出了三维楔形体计算模型的概念.Jaucsccz[4]在Horn[3]的基础上，假设地层均匀，分析了上覆土的松动效应对极限支护力的影响.秦建设[5]结合前人[2-4]成果得到适用于均质土层的极限支护力表达式.日本Fujita[6]基于楔形体模型提出二维对数螺旋线模型，避免了三维楔形体模型复杂的计算.乔金丽[7]给出考虑渗流影响的支护力表达式.雷明锋[8]引入线路坡度，得到了不同坡度下极限支护力的大小.陈仁朋[9]将三维楔形体模型应用于开挖面发生破坏时地表可能发生隆起的情况，拓展了筒仓理论的应用范围.上述研究均针对均质土层，而实际工程中时常穿越上下层土质各异的复杂地层，刘栋[10]根据数值模拟结果得到了上软下硬地层中的开挖面主要在上层土体发生破坏的结论，并提出了适用于复合地层的计算模型，但未给出具体计算表达式.陈强[11]根据其数值结论，建立了适用于该地层条件的局部楔形体模型，假定开挖面仅在上层土质较差土体发生破坏，即滑动破裂面仅跨越上层土质相对较差土体；既而得到相应计算公式，并分析了上层土体对支护力的影响.而对于盾构隧道跨越上硬下软地层开挖面极限支护力鲜有针对性研究，传统楔形体模型对此采用滑动面为直线的单滑体，仅以上下层土体强度指标进行加权等效计算，该法是否合理值得商榷.

本文在前人基础上，考虑地层的成层不均性，提出适用于上硬下软地层条件下的模型并得到极限支护力公式，将其与数值结果相对比，验证该方法的合理性；并与传统方法进行比较.最后进行参数分析，得到有益结论，以期进一步完善盾构隧道开挖面极限支护力计算理论.

1建立理论模型

1.1基本假设

不同于文献[11]所假设的当隧道经过上软下硬地层时，开挖面仅在上层软土发生局部破坏，滑动面仅跨越上层，其滑动形态为直线，现将传统的适用于均质土层的楔形体模型进行改进，基于极限平衡法，建立本文的计算模型，结合前人研究成果，为适应开挖面土层上硬下软的情况，本文假设开挖面发生整体破坏，滑动面跨越隧道穿越的上下两个地层；并对传统的筒仓模型进行改进，取开挖面土体的滑动面为折线，滑体分为上下两个楔形体[10]，滑动面与水平面所成夹角的大小与土体的内摩擦角有关，符合q=45o+φ/2[5].

根据筒仓理论[2]并结合上述分析，计算模型如图1所示，abhg为隧道开挖面，klmn为地表，abhgijef为隧道开挖面失稳时的下滑土体，bfjh,aeig和abfjie为滑动面，klmn-ghji为下滑土体abhgijef所带动的上部下沉土体，θ1与θ2分别为下、上土层的破坏角，D1和D2分别下、上土层的厚度.

图1　上硬下软地层楔形体模型

结合传统筒仓理论[2]基本假定，改进后模型的基本假定如下:

1) 各层土体是各向同性的，滑裂面上的土体符合摩尔-库仑准则；

2) 矩形abhg的面积等于盾构开挖面的面积；

3) 楔形体顶面及倾斜滑动面应力均匀分布；

4) 不考虑楔形块内部的应力分布.

1.2 楔形体自重G

如图2,图3所示，G1与G2分别为下层和上层土体重力，由楔形体的几何关系可得:

(1)

(2)

式中B为隧道开挖面宽度;γ为土体重度.

1.3楔形体上的上覆土压力PV0

上覆土压力应力σv0采用太沙基松动土压力理论[14]所得研究成果:

(3)

(4)

(5)

则可得作用于楔形体上的上覆土压力PV0:

(6)

其中D为盾构隧道直径;γ为土体重度;c为土体粘聚力;φ为土体内摩擦角,对于棱柱体中的成层土,采用其加权平均值；P0为超载；Ks为土体侧压力系数,符合Ks=1-sinφ[15].

图2　上层楔形体受力示意图

图3　下层楔形体受力示意图

1.4竖直滑动面上的剪力T

对于竖直滑动面bfjh(aeig)的计算，可按照图4所示进行计算，假定楔形体bfd(aec)和fjhd(eigc)滑动面上的竖向应力分别随深度呈线性增加，又楔形体顶面ghji上的竖向应力为σV0，则滑动面bfd(aec)和dfjh(ceij)各点处的竖向应力σV(z)为:

σV1(z1)=σV0+γ2D2+γ1z1,

0≤z1≤D1

(7)

σV2(z2)=σV0+γ2z2,

0≤z2≤D2

(8)

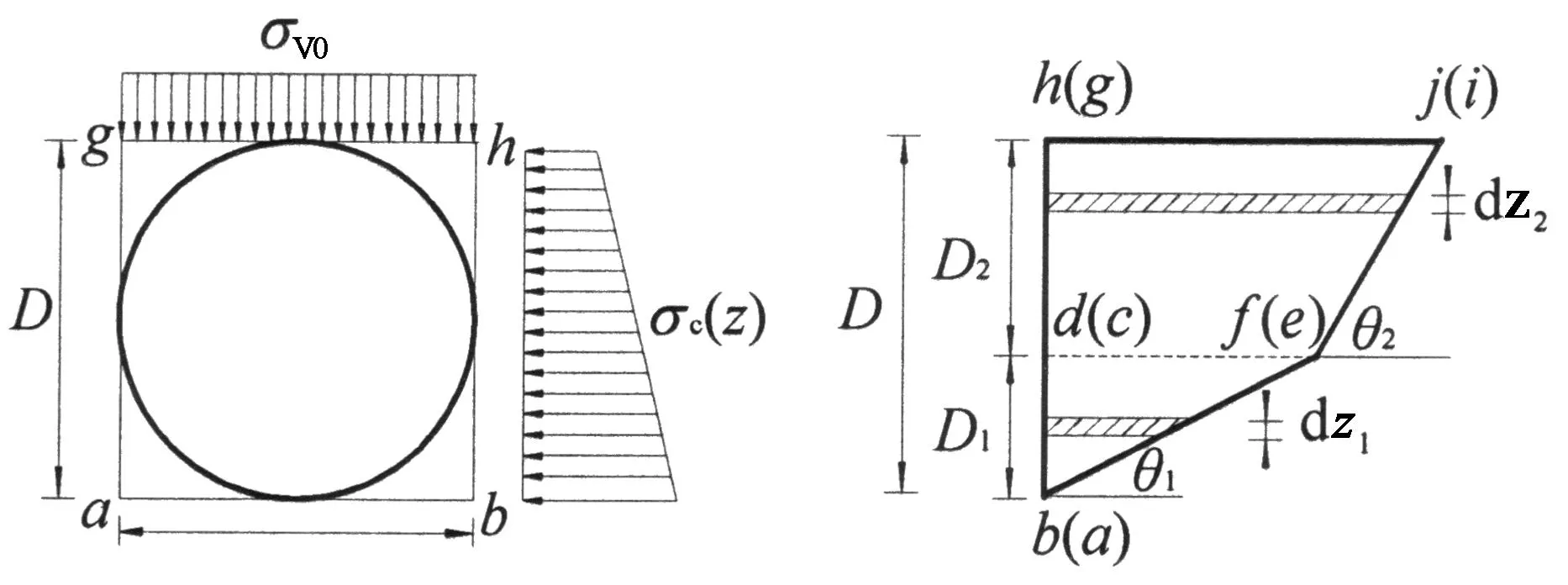
图4　剪力T计算示意图

由传统筒仓理论[2]可得afjh(aeig)滑动面上任意点处的侧压力σc(z)为:

σc=KσV

(9)

分别取bfd(aec)和dfjh(ceij)滑动面上-微元面积，则作用于该微元面积上的剪力dT为:

(10)

即：

(11)

(D2-z2)cosθ2]dz2

(12)

对其进行积分,则可求得作用于bfd(aec)和dfjh(ceij)滑动面上的剪力T:

(13)

(14)

式中K为土体侧压力系数，符合K=1-sinj[15].

1.5倾斜滑动面上的剪力F

(15)

(16)

式中N为倾斜滑动面上的法向力.

1.6开挖面上的支护力P

考虑楔形体的平衡，对两楔形块体分别建立水平和竖直方向的平衡方程.

下地层:

P1+2T1cosθ1+F1cosθ1=N1sinθ1

(17)

Q1+G1-P1-2T1sinθ1=

F1sinθ1+N1cosθ1

(18)

上地层:

P2+2T2cosθ2+F2cosθ2=N2cosθ2

(19)

PV0+G2=P2+Q2+2T2sinθ2+

F2sinθ2+N2cosθ2

(20)

Q1=Q2

(21)

考虑到支护力均匀分布[8]，则有:

(22)

联立(1),(2),(6),(13) ～ (22)各式求解，可得复杂地层中盾构开挖面支护力P的表达式:

(23)

其中:

(24)

(25)

(26)

(27)

2数值模拟

2.1基本假设

本文基于ADINA数值计算软件进行盾构开挖面稳定性数值模拟，结合前人研究成果[16-20]，为提高运算效率，在进行有限元分析计算时，作如下假定:

1) 同一地层土体为各向同性材料，符合摩尔-库仑强度准则；

2) 不考虑地下水的作用.

2.2计算模型

以文献[16]所述盾构施工时常穿越上硬下软地层为工程背景.据此建立计算模型，如图5所示，土层从上往下依次为杂填土、淤泥质土、中密状残积层和洪积层软土层4个土层，隧道跨越不同土层.材料计算参数如表1所示.

图5　地层分布及隧道埋深

2.3数值计算结果

根据上述情况，本文所建模型共由24 185个节点组成，分为22 100个单元，其中土体单元为22 000个，采用三维八节点模拟.为观察开挖面稳定状态的演化过程，在开挖面施加与原始地应力大小相同的支护力，逐渐减小支护压力，同时记录开挖面前方土体的水平位移变化.

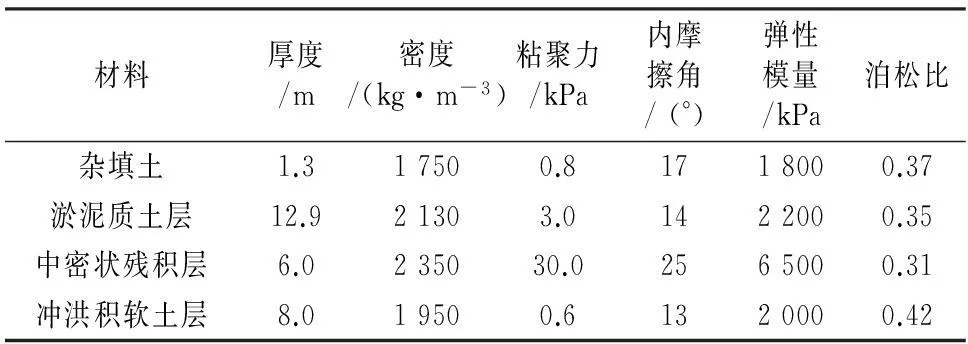
表1　材料计算参数

为直观表示开挖面稳定状态与支护应力及埋深的关系，引入应力支护比λ[18]，λ=σs/σ0，其中σ0为原始土层中水平应力，可用σ0=K0γz计算，则开挖面中心点支护力为σs=λK0γz.图2表示的便是支护应力比λ与开挖面水平位移的关系.

图6则分别为支护应力比λ为0.80和0.15时开挖面水平位移图.结合图6,图7可知，开挖面支护力的大小影响隧道周围土体的变形，当支护力小于原始静止土压力时，开挖面前方土体将向盾构压力仓内移动，随着支护应力的减少，开挖面中心点的位移逐渐增大，当支护应力比为0.15时，测点水平位移急剧增大，开挖面支护力为37.37 kPa，根据前人研究成果[20]，将该支护力定义为极限支护力.

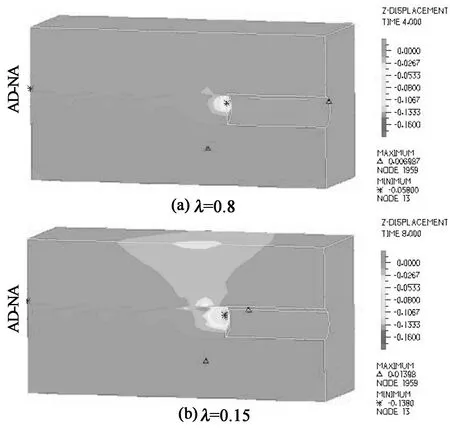
图6　开挖面土体水平位移图

3模型验证

为证明对开挖面分层的必要性，同时验证由本文模型的正确性与合理性,现将各方法所得到的极限支护力进行比较，其中,当D1=D,D2=0,且土体强度指标采用上下层加权平均值时,则退化为不考虑分层的方法；比较结果如表2所示.

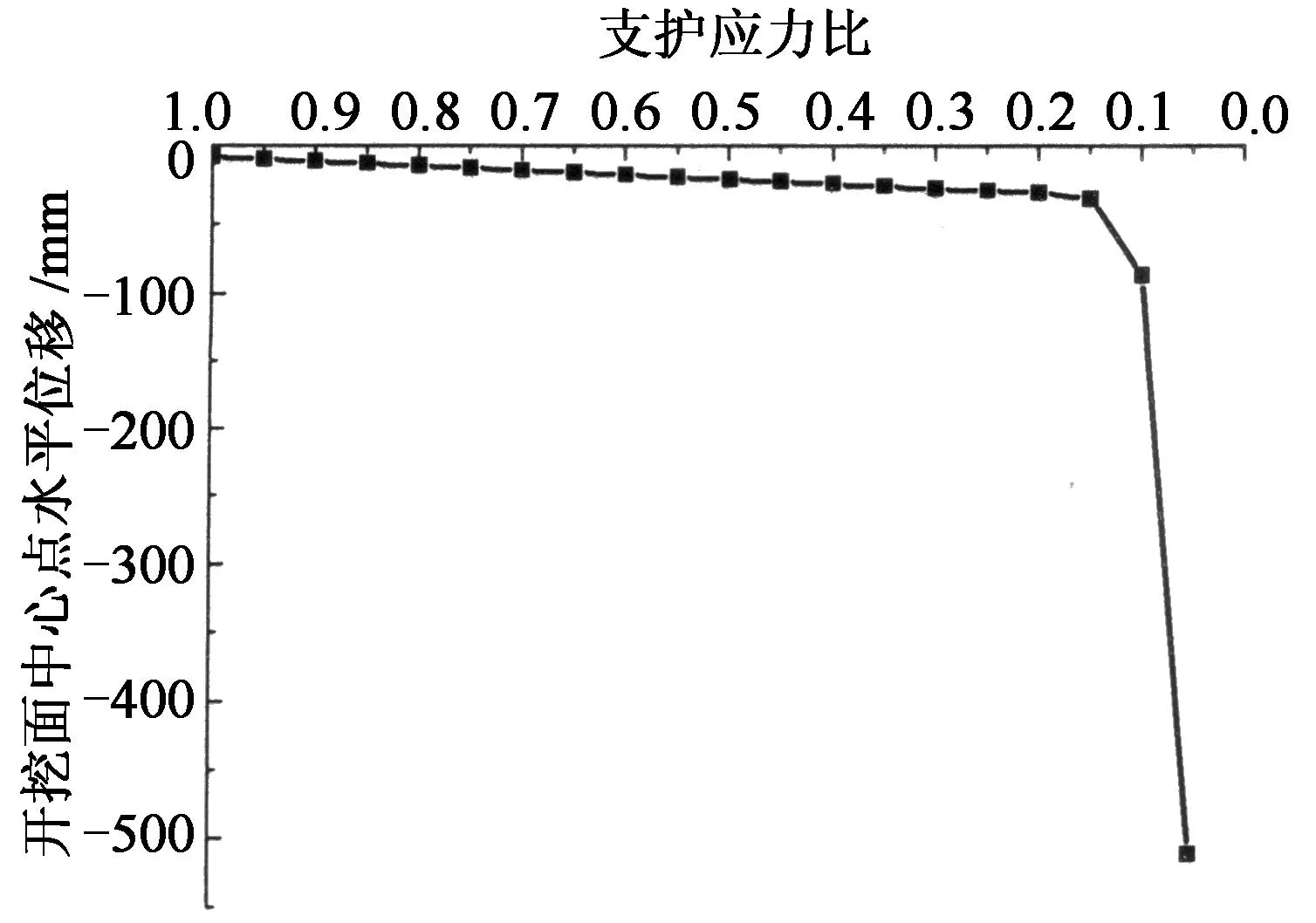
图7　支护应力比与开挖面中心点水平位移关系

数值模拟文献[11]考虑分层不考虑分层p/kPa37.3712.4141.2851.75

通过表2可知，数值模拟与本文方法所得结果较传统方法更为吻合，表明该方法的正确性与本文假设滑体分为上下两个楔形体的合理性，同时说明了当开挖面遭遇上硬下软的复合地层时，考虑破坏面的分层是有必要的.

由文献[11]参考方法可知，所得结果与数值模拟以及本文推荐方法差异较大，且通过观察数值模拟云图结果，可知开挖面横跨上下两个土层，而不仅仅在上土层发生破坏，由此说明了应用该法在分析此种工况时的不恰当性.

4参数分析

为进一步分析埋深、开挖面土层厚度以及土体强度指标对极限支护力的影响,以上述工程参数为基础，作如下参数分析．

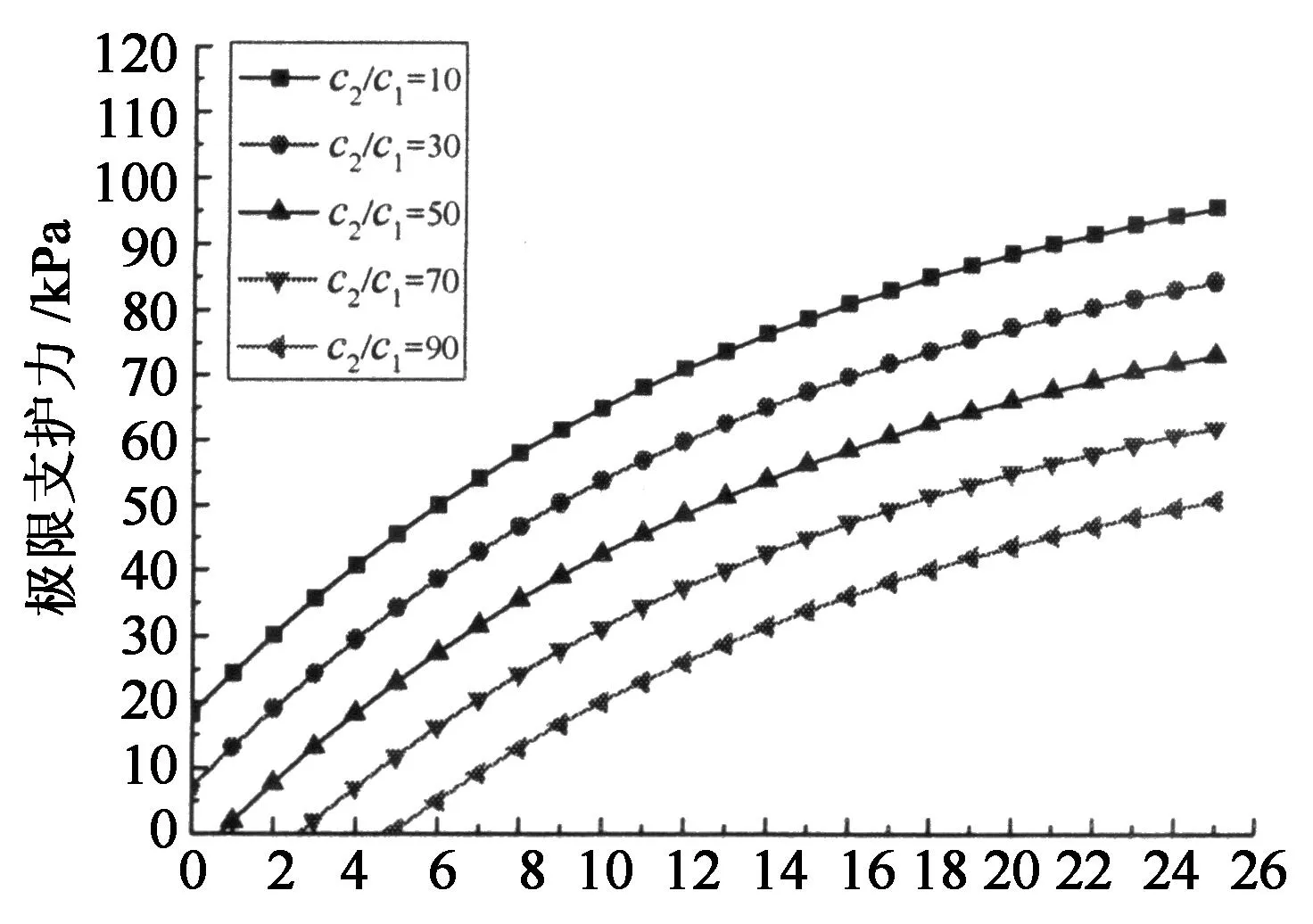
4.1黏聚力c

由图8可知，黏聚力一定时,极限支护力随埋深增加而增大，但增长速率逐渐减缓；当埋深增长到一定程度时,极限支护力将不再增长.

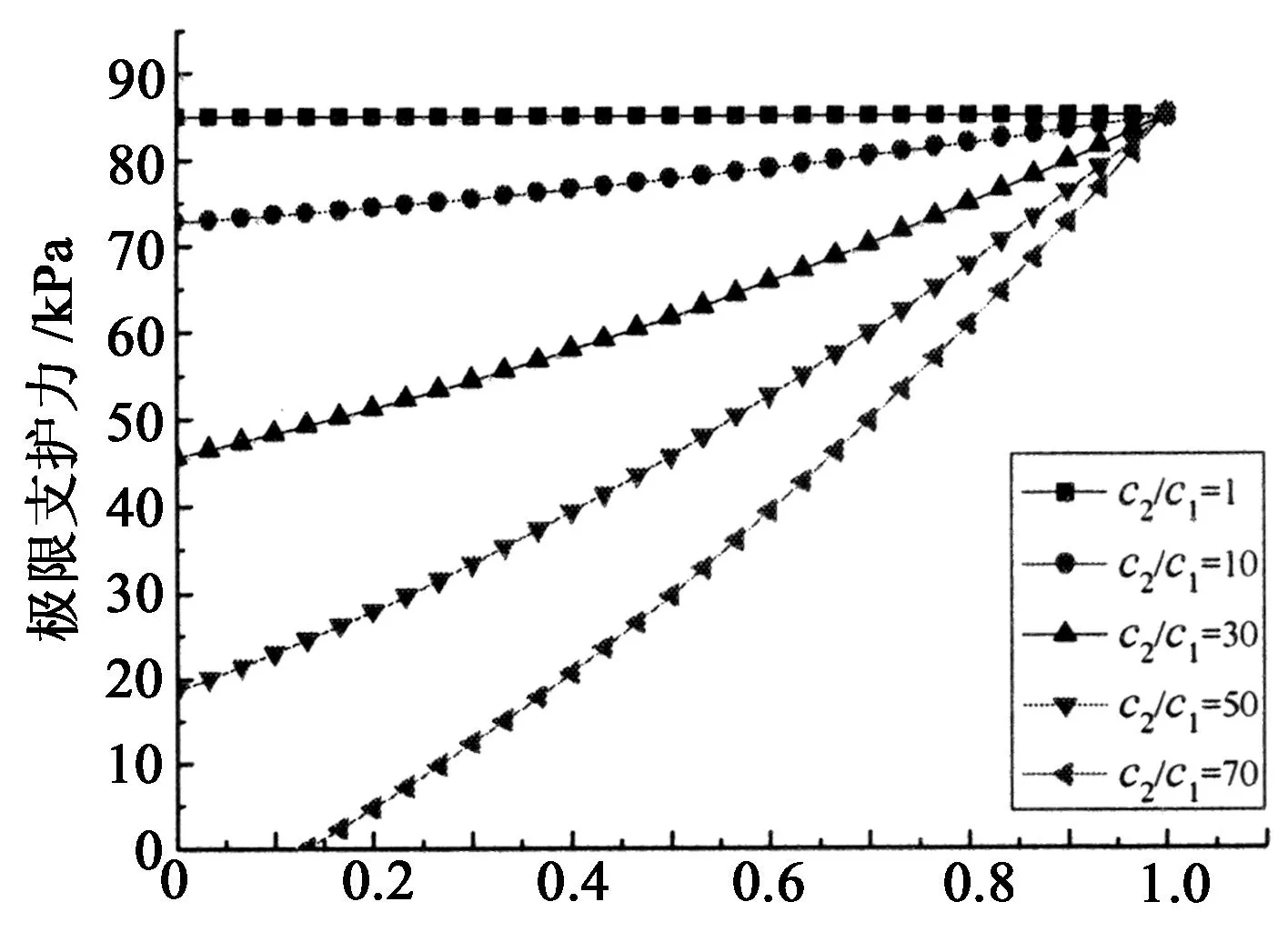
由图9可知,当上下土层内摩擦角相等时，若黏聚力比值不大,两种方法所得结果接近；随着比值增大,曲线出现分离；此时不考虑分层算法较本文考虑分层的方法结果偏大.

由图10可知,在厚度比一定时,支护力随黏聚力呈近似线性增长；随着黏聚力比增大而出现非线性增长.

埋深/m

埋深/m

D1/D

由图11可知，随着上下层黏聚力差异变大，两曲线出现分离，在上下层厚度相等时差值最大；当土层为为均质土层时，两种方法所得结果一致；且不考虑分层的方法所得曲线呈线性变化.

4.2内摩擦角φ

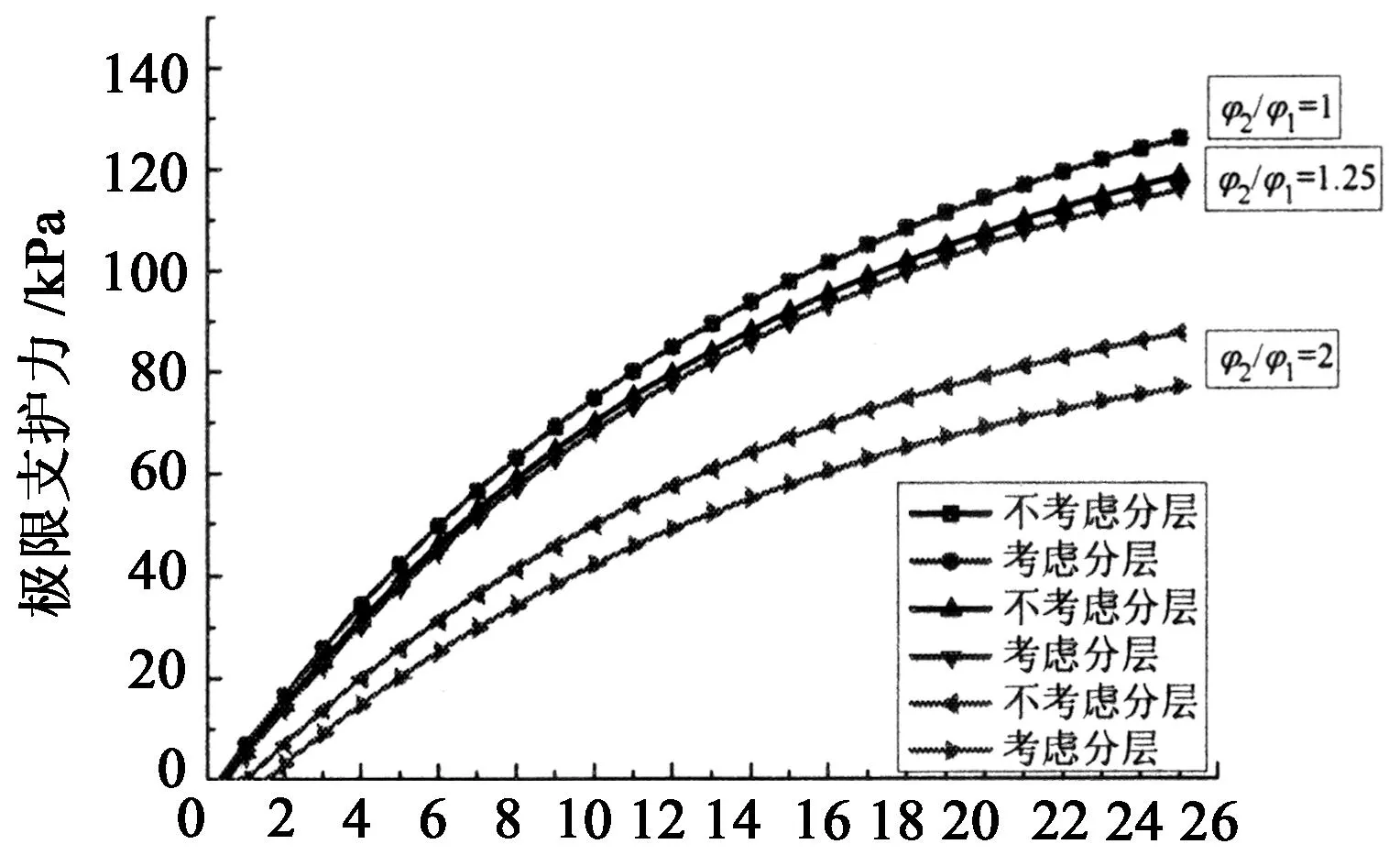
由图12可知，内摩擦角一定时，极限支护力随埋深增加而增大，但增长速率减缓.

D1/D

埋深/m

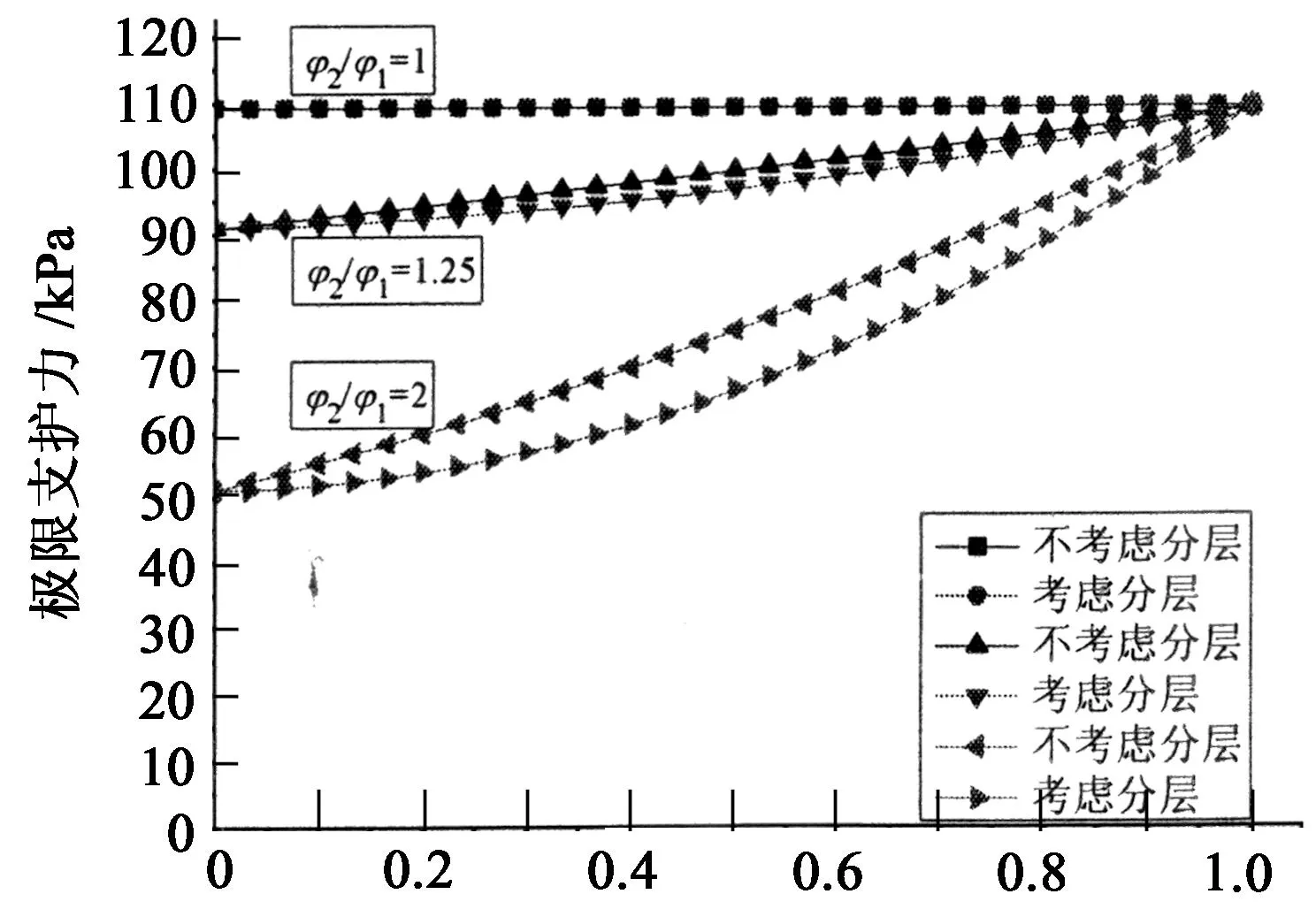
由图13可知，当上下土层内摩角相差不大时，二者所得结果接近；随着内摩擦角比增大，支护力减小，两种情况所得结果差值增大.

埋深/m

由图14可知，厚度比一定时,支护力随内摩擦角以递增速率增长；当上层硬土较下层软土厚时，支护力对内摩擦角很敏感，需予以考虑.

由图15可知，内摩擦角比较小时，两种方法所得结果接近；当其比值增加时，二者的差值随之增大，并在上下层厚度相等时二者之差取最大值.

D1/D

D1/D

4.3对比分析

将图13,图15与图9,图11分别进行对比，可知支护力对内摩擦角的敏感程度较黏聚力要大，笔者认为，这是由复合地层中楔形体滑动面的破坏机理所决定的.黏聚力对考虑分层与否所造成的差异，体现在不考虑分层算法以土体加权平均值来简单考虑地层的成层性,而内摩擦角则还将影响到滑动面行程.不考虑分层算法所得结果偏大，主要原因是其采用的直线滑裂面模型在滑动行程上短于考虑分层算法所采用的折线滑裂面模型，从而低估了开挖面的强度.

5结语

1) 本文基于筒仓理论和极限平衡法,提出适用于上硬下软地层的计算模型并得到极限支护力表达式.本文方法计算结果与数值结果相对吻合，说明以适用于上软下硬地层的局部楔形体模型与适用于均质土层的直线滑动面楔形体模型来分析上硬下软地层中的开挖面极限支护力并不合适，同时也表明了本文假定的整体破坏模型和滑体分为上下两个楔形体的合理性.

2) 极限支护力随埋深增大而增大，但增大到一定程度时将不再增长.而地层情况较均匀，土体强度参数差异不大时，考虑分层与否所得结果较为吻合；但在上下地层土体强度指标相差较大时，其结果差异较大.

3) 本文方法所假设模型尚未考虑地下渗流和线路坡度对支护力的影响,因此，对盾构开挖面极限支护力的研究有待进一步探讨.

参考文献

[1]关宝树.地下工程[M].北京:高等教育出版社,2006:185-187.

GUAN Bao-shu. The underground engineering[M]. Beijing: Higher Education Press, 2006:185-187. (In Chinese)

[2]JANSSEN H A. Versuche fiber getreidedruck in silozellen[J]. Zcitschrift des Vereins Dcutscher Ingenieure, 1895,39(35): 1045-1049.

[3]HORN M. Horizontal earth pressure on perpendicular tunnel face[C]//Proceedings of the Hungarian National Conference of the FoundationEngineer Industry, Hungarian: Budapest, 1961:7-16.

[4]JANCSECZ S, STEINER W. Face support for a largemix-shield in heterogeneous ground conditions[C]//Proceedings of Tunnelling’ 94. London, Chapman and Hall, 1994:531-549.

[5]秦建设.盾构施工开挖面变形与破坏机理研究[D].南京:河海大学土木工程学院，2005:85-86.

QIN Jian-she. Study on deformation and failure mechanism and the face shield excavation[D]. Nanjing: Civil Engineering College, Hohai University,2005:85-86. (In Chinese)

[6]FUJITA K Kusakabe. Underground construction in soft ground[M]. Rotterdam:Balkema A A, 1995:337-343.

[7]乔金丽,张义同,高健.考虑渗流的多层土盾构隧道开挖面稳定性分析[J].岩土力学, 2010,31(5) :1497-1502.

QIAO Jin-li, ZHANG Yi-tong, GAO Jian. Tability analysis of shield tunnel face in multilayer soil with seepage[J]. Rock and Soil Mechanics, 2010,31(5):1497-1502. (In Chinese)

[8]雷明锋,彭立敏,施成华,等.迎坡条件下盾构隧道开挖面极限支护力计算与分析[J].岩土工程学报,2010,32(3) :488-492.

LEI Ming-feng, PENG Li-min, SHI Cheng-hua,etal. Calculation and analysis of limit support force of shield tunnel excavation face under facing-slope conditions[J]. Eotechnical Engineering, 2010,32(3):488-492. (In Chinese)

[9]陈仁朋,齐立志,汤旅军,等.砂土地层盾构隧道开挖面被动破坏极限支护力研究[J].岩石力学与工程学报,2013,32(1):2877-2882.

CHEN Ren-peng, QI Li-zhi, TANG Lv-jun,etal. Sand formation of shield tunnel excavation face passive failure limit supporting force [J]. Journal of Rock Mechanics and Engineering, 2013,32(1): 2877-2882. (In Chinese)

[10]刘栋.复合地层中土压盾构隧道开挖面稳定性研究[D].武汉:华中科技大学土木工程与力学学院,2009:29-51.

LIU Dong. Study on stability of tunnel excavation face for EBP shield machine in composite ground[D]. Wuhan: Civil Engineering and Mechanics College, Huazhong University of Science and Technology,2009:29-51. (In Chinese)

[11]陈强.上软下硬地层中盾构隧道开挖面支护压力研究[D].武汉:华中科技大学土木工程与力学学院,2010:16-18.

CHEN Qiang. Study on support pressure at excavation face of shield tunneling in composite ground with soft and underlying hard strata[D]. Wuhan: Civil Engineering and Mechanics College, Huazhong University of Science and Technology,2010:16-18.(In Chinese)

[12]杨峰,阳军生,张学民,等.黏土不排水条件下浅埋隧道稳定性上限有限元分析[J].岩石力学与工程学报,2010,29(2):3952-3959.

YANG Feng, YANG Jun-sheng, ZHANG Xue-min,etal. Finite element analysis of upper bound solution of shallow-buried tunnel stability in undrained clay[J]. Journal of Rock Mechanics and Engineering, 2010,29(2):3952-3959. (In Chinese)

[13]吕玺琳,王浩然.软土盾构隧道开挖面支护压力极限上限解[J].土木建筑与环境工程,2011,33(2) :65-69.

LV Xi-lin, WANG Hao-ran. Upper bound solution of the limit support pressure during shield tunneling in soft clay[J]. Civil and Environmental Engineering, 2011,33(2):65-69. (In Chinese)

[14]TERZAGHI K. Theoretical soil mechanics[M]. New York: John Wiley and Sons,1943: 66-76.

[15]SCHMIDT B.Discussion on ‘Earth pressure at rest related to stress history’[J]. Canadian Geotechnical Journal, 1996,3(4):239-242.

[16]权永华.上硬下软地层盾构施工[J].城市建设理论研究, 2011,1(36) :121-123.

QUAN Yong-hua. Hard on the soft stratum of shield construction[J]. Urban Construction Theory Research, 2011,1(36):121-123. (In Chinese)

[17]张如林,楼梦麟,袁勇.土-海底沉管隧道体系三维地震响应分析[J]. 湖南大学学报:自然科学版,2014,41(4):25-32.

ZHANG Ru-lin, LOU Meng-lin, YUAN Yong. Three-dimensional seismic respones analysis of soil-undersea immersed esponse analysis tunnel system[J].Journal of Hunan University:Natural Sciences, 2014, 41(4):25-32. (In Chinese)

[18]乔金丽,张义同,高健,等.强度折减法在盾构隧道开挖面稳定分析中的应用[J].天津大学学报,2010,43(1):14-20.

QIAO Jin-lin,ZAHNG Yi-tong,GAO Jian,etal. Application of strength reduction method to stability analysis of shield tunnel excavation[J]. Journal of Tianjin University, 2010,43(1):14-20. (In Chinese)

[19]苏永华, 毛克明, 梁斌,等. 基于峰后特征的深部隧道围岩分层断裂数值分析[J]. 湖南大学学报:自然科学版, 2014, 41(9):79-85.

SU Yong-hua, MAO Ke-ming, LIANG Bin,etal. Numerical analysis of the layered fracture within surrounding rock in deep tunnel based on post-brittleness[J]. Journal of Hunan University: Natural Sciences, 2014,41(9):79-85. (In Chinese)

[20]秦建设,尤爱菊.盾构隧道开挖面稳定数值模拟研究[J].矿山压力与顶板管理,2005,22(1) :27-30.

QIN Jian-she, YOU Ai-ju. Numerical simulation of stability of tunnel excavation face for shield machine[J]. Mine Pressure and Roof Management, 2005,22(1):27-30. (In Chinese)

Analysis of Limit Supporting Force of Tunnel Excavation Face for Shield Machine in Upper-hard Lower-Soft Ground

ZHAO Ming-hua1†, MAO Tao, NIU Hao-yi, LIU Meng

(Geotechnical Engineering Institute, Hunan Univ, Changsha，Hunan410082, China)

Abstract:Limit support pressure is a key parameter to keep the stability of the excavation face in shield tunnel excavation, but there has been little research on the limit supporting force of tunnel excavation face for shield machine in upper-hard lower-soft ground． Based on the limit equilibrium method, silo theory and hypothesis of sliding surface being a broken line, the limit supporting force calculation model and formula of excavation face for shield tunnel in upper-hard lower-soft ground were established. To check the rationality of the model and the necessity of considering layers, comparative numerical analyses were conducted. The agreement between the two methods is very good. The effect of buried depth, thickness of upper and lower soil layer, cohesion and internal friction angle on limit support force was analyzed. It shows that the results are different when considering layered or not when the layer is uneven. Therefore, it cannot be equated with homogeneous soil, which should be considered in engineering practice.

Key words:shield tunnel; upper-hard lower-soft ground; limit support force; silo theory; the limit equilibrium; numerical simulation

中图分类号：TU456.3

文献标识码：A

作者简介：赵明华(1956-)，男，湖南邵阳人，湖南大学教授，博士生导师 †通讯联系人，E-mail: mhzhaoohd@21cn.com

*收稿日期：2015-04-03基金项目：国家自然科学基金资助项目(51278187)，National Natural Science Foundation of China(51278187); 长沙市科技项目(K1203011-11)

文章编号：1674-2974(2016)01-0103-07