基于车桥耦合的钢管混凝土拱桥车桥冲击系数研究

韩艳，李浩，薛繁荣

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)



基于车桥耦合的钢管混凝土拱桥车桥冲击系数研究

韩艳，李浩，薛繁荣

(长沙理工大学 土木与建筑学院，湖南 长沙 410004)

摘要:以某钢管混凝土拱桥为研究对象，利用ANSYS软件建立了该桥的三维有限元模型，然后基于两轴车辆模型作用下的车-桥耦合振动模型，自编车桥耦合振动程序从路面粗糙度、行车速度、行车数量和行车间距4个方面对钢管混凝土拱桥的动力响应和冲击系数进行分析，计算结果表明：路面粗糙度、车辆行驶速度、车辆数量以及车辆间距对桥梁冲击系数均有一定程度的影响，所得出的结论可为钢管混凝土拱桥设计及后期养护提供参考。

关键词：钢管混凝土拱桥； 车桥耦合振动； 有限元模型；冲击系数

近年来，钢管混凝土拱桥因具有承载能力高、跨越能力强、抗震性能好等优点得到了飞速发展，被越来越多的实际工程所运用，然而，在实际应用过程中，这类桥梁的行车舒适性问题却十分突出，成为广大研究者关注的对象。钢管混凝土拱桥由于结构自重较轻、刚度较小，尤其是中、下承式拱桥悬吊桥道系常采用漂浮体系，整体性较差，桥面振动问题较为突出，对桥梁的使用性能有较大的影响。而目前，钢管混凝土拱桥一般采用中、下承式结构，吊杆较长，活载在总荷载中所占比重较大，因此动力作用显著，加上这类桥梁复杂的造型使其在车辆作用下振动机理变得十分复杂，为保证车辆在桥上行驶的舒适性，对该类桥梁在车辆作用下的冲击效应进行研究显得尤为重要。对车桥耦合作用时的动力研究，许多研究者已经对梁式桥、缆索承重体系桥和传统拱桥进行了较多的探索[1-5]，而对于钢管混凝土拱桥的研究还相对较少。吴庆雄等[6]采用有限元模型对钢管混凝土拱肋和桥道系的加速度、速度动力响应和冲击系数进行了对比分析，提出了不同路面平整度下中、下承式钢管混凝土拱桥车桥动力响应的近似公式。Huang[7]研究了上承式钢管混凝土拱桥的动力特性和冲击系数，分析了桥面、立柱和拱肋的边界条件对冲击系数的影响，并将计算得到的冲击系数与相应的规范结果进行对比，得到了一些有意义的结论。孙潮等[8]通过收集多座钢管混凝土拱桥的实测冲击系数，并对其进行回归分析得出了钢管混凝土拱桥冲击系数的简化计算公式。严志刚等[9]提出了一种车-桥振动简化计算方法，计算分析了不同等级桥面下的汽车冲击荷载系数。李岩等[10]对异形钢管混凝土拱桥的冲击系数做了一定研究。陈灏等[11]利用有限元软件建立了桥梁模型，建立了1/4车辆模型作用下的拱桥车桥耦合振动模型，分析了不同因素对系杆拱桥的冲击系数的影响。综上所述，国内外学者对冲击系数进行了广泛的研究并取得了一定成果，但是几乎大部分都是采用近似的计算方法，车辆模型也相对较简单而且我国规范对于桥梁冲击系数的计算只考虑了结构的基频[12]，实际上冲击系数还与路面粗糙度等一系列因素有关，所以对于冲击系数的计算还有待进一步研究和完善。本文以某钢管混凝土拱桥为研究对象，利用通用有限元软件ANSYS建立该桥的三维有限元模型，然后基于两轴车辆模型作用下的车-桥梁耦合振动模型，应用自编车桥耦合振动分析程序，研究移动车辆作用下不同路面粗糙度、不同车辆行驶速度、不同数量车辆以及不同车辆间的行驶间距对钢管混凝土拱桥的冲击系数的影响。

1工程概况

以某钢管混凝土拱桥为研究背景，其跨径组合为10×20 m(引桥)+530 m(主跨)+4×20 m(引桥)，引桥为预应力钢筋混凝土带翼小箱梁，主跨为钢管混凝土中承式拱桥，主孔净跨径为500 m(跨度为518 m)，净矢跨比为1/4.5，拱轴系数为1.75，拱脚截面高16.0 m，拱顶截面高8.0 m，拱上吊杆和立柱间距均为14.3 m，桥面梁为“工”型格子梁，桥面板为钢-混凝土组合桥面板。桥跨布置如图1所示，该桥结构复杂，跨径为钢管混凝土拱桥世界之最，被誉为“世界第一跨”，故对其冲击系数研究具有代表意义。

图1　桥跨总体布置图Fig.1 Layout of the bridge span

2车桥耦合振动分析方法

2.1车辆模型

现实中车辆类型有很多种，分别对应的车辆模型有2轴、3轴、4轴甚至更多，车辆模型虽然轴数不同但其研究方法类似。本文采用2轴4轮车辆模型对冲击系数进行分析，该车辆模型由1个刚性车体、4个车轮和一系列的弹簧和阻尼组成，其中车轮模拟为质量块，如图2所示。车辆的悬挂系统和车轮的弹性均由弹簧模拟，悬挂系统耗能能力由黏滞阻尼模拟，并作以下假设：车轮与桥面始终不分离，悬挂系统以及车轮的质量均集中在车轮质量块上，弹簧和阻尼装置的质量均为0。车辆的刚性车体考虑了竖向Zvr，侧向Yvr，侧倾φvr以及俯仰θvr4个自由度，每个车轮考虑了竖向位移ZsL(R)i和横向位移YsL(R)i2个自由度。因此，对于2轴4轮车辆模型，共有12个自由度。

通过虚功原理或者拉格朗日法可以建立车辆运动方程，本文采用拉格朗日法建立的车辆运动方程可表示为：

(1)

其中，T，V和R分别为车辆运动系统的总动能、总弹性势能和总耗散能力；qvk为车系统的自由度坐标；Qvk是对应于坐标qvk的广义力函数，可通过虚功原理计算得到，其表达式为：

(2)

(a)侧面图；(b)断面图图2　车辆模型Fig.2 Vehicle model

由车辆运动系统的总动能T，总弹性势能V，总耗散能力R以及广义力函数Qvk可以得到车辆系统的各个自由度的运动方程，并把运动方程写成矩阵形式可表示为：

(3)

其中，Mv，Cv和Kv分别为车辆的质量矩阵、阻尼矩阵和刚度矩阵；Fv为作用在车辆的外荷载向量，由车桥间相互作用产生；qv={ZvrθvrφvrYvrZSL1ZSR1ZSL2ZSR2YSL1YSR1YSL2YSR2}T为车辆的位移向量。

2.2桥梁模型

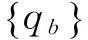
{qb}=[{Φ1}{Φ2}…{Φn}]

{ξ1ξ2…ξn}T=Φ{ξ1ξ2…ξn}T

(4)

式中，n为所取的振型阶数；{Φi}和ξi分别为第i阶的模态振型和模态坐标；Φ为桥梁结构的模态矩阵。本研究通过ANSYS建立桥梁有限元模型，获得桥梁结构的模态矩阵和模态频率，如果计算模态时振型是关于最大值归一化的，最后桥梁结构的运动方程表示为:

(5)

将式(5)关于模态质量归一化得

(6)

式中：ωi为桥梁结构的第i阶模态频率；ζi为桥梁结构的第i阶模态阻尼比。

2.3车桥耦合方程

车桥间的相互作用主要通过车桥自身运动对相互双方发生作用，假设车轮与桥面始终接触，车辆和桥梁在车轮与桥面接触处具有相同的位移协调条件，并考虑桥面的路面粗糙度的影响。如果将车辆所受桥梁作用的广义力函数和桥梁所受车辆作用力代入各自系统的运动方程，可得车桥系统的耦合运动方程为：

(7)

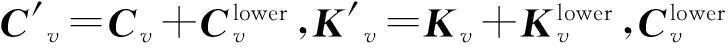
本文采用四阶龙格-库塔法对车桥耦合振动方程进行求解，依据车桥耦合振动理论，采用MATLAB编制了车-桥耦合振动分析程序。

2.4路面粗糙度模型

路面粗糙度是影响车辆和桥梁动力响应的一个重要因素，其均值为0，属于各态历经的平稳Guass随机过程。在工程实际中，通常用功率谱密度来描述路面的统计特性，Dodds等[14]提出的公路路面粗糙度的功率谱密度函数为：

(8)

式中：S(n)为路面粗糙度的功率谱密度函数(m3/cycle)；S(n0)为粗糙度系数，其值由路况确定，文中将路面的粗糙度划分为“很好”，“好”，“一般”，“差”和“很差”5个等级，与之对应的粗糙度系数分别为5×10-6，20×10-6，80×10-6，256×10-6，1 280×10-6m3/cycle；n为分散频率(cycle/m)；n0为截断频率，等于1/2π。

路面粗糙度可以用傅立叶逆变换生成为

(9)

式中，nk为0～2π均匀分布的随机相位。

3钢管混凝土拱桥耦合振动响应及冲击系数分析

根据上述计算模型与计算原理对该钢管混凝土拱桥进行空间车桥耦合振动分析，得到车桥耦合振动响应，研究路面粗糙度、车辆行驶速度、车辆数量、车辆行驶间距等因素对车桥动力响应以及冲击系数的影响。

3.1结构动力特性分析

运用ANSYS对该大桥进行模态分析，前10阶振型和频率如表1所示。

3.2基于车桥耦合的冲击系数影响分析

车辆荷载的冲击系数是车辆过桥时对桥梁结构产生的动力效应的增大系数。汽车荷载的冲击系数可表示为 ：

(10)

式中：Rdm(xi)和Rsm(xi)分别为车辆过桥时截面xi处桥梁结构的最大动力、静力响应。

表1　钢管混凝土拱桥前10阶动力特性

单辆车辆行驶在该桥上在跨中竖向的静、动位移曲线如图3所示。从图中可以看出，跨中竖向最大静位移为1.80 mm，动位移始终围绕着静位移上下波动。车辆位于跨中时对跨中静、动位移影响最大，车辆远离跨中时对跨中的静、动位移影响较小。

图3　跨中竖向静、动位移曲线Fig.3 Static and dynamic vertical displacement curves at the middle of the span

为了研究各种因素对冲击系数影响，假设车辆均匀行驶在不同路面时对桥梁振动的响应，分析各种因素对冲击系数的影响。桥梁结构的各阶阻尼比均取0.05。

3.2.1路面粗糙度的影响

为研究路面粗糙度对桥梁和车辆动力响应的影响，取5种粗糙度(非常好、好、一般、差和非常差)情况进行研究，车辆行驶速度为20 m/s，考虑一辆车辆，车辆距桥中心线的距离为10 m，为了考虑车辆的初始位移的影响，车辆初始位置位于桥梁左侧200 m处。图4为桥梁跨中竖向位移时程曲线。

由图4可知，相同车速下，路面状况越差，动挠度围绕静挠度上下波动的幅度越大，最大动挠度随路况的恶化而增大。

图4　桥梁跨中竖向位移时程Fig.4 Time history of the vertical displacement at the middle of the span

表2为单辆车辆以20 m/s速度通过不同粗糙度情况路面时跨中位置的最大动位移及冲击系数。

从表2可以看出，在相同车速下，冲击系数随着粗糙度的增加而增大，路面越不平顺，冲击系数越大。因此在桥梁服役期间要加强桥梁的养护，及时对桥面铺装层进行维护，这对于保证桥梁结构的安全性和行车舒适性意义重大。

3.2.2车辆行驶速度的影响

为研究行车速度对桥梁的动力响应，车辆行驶速度分别取40,60,80和120 km/h，车辆数量为1辆，车辆距桥中心线的距离为10 m，路面粗糙度取为一般路面情况，为了考虑车辆初始位移的影响，车辆初始位置位于桥梁左侧200 m处。图5为车辆以不同速度上桥后桥梁跨中竖向位移随着时间变化的曲线。图6为车辆以不同速度上桥后桥梁跨中竖向位移随着桥梁纵向位移变化的曲线。表3为单辆车辆以不同速度行驶在桥上时跨中位置的最大动位移及冲击系数。

图5　桥梁跨中竖向位移时程Fig.5 History of the vertical displacement at the middle of the span

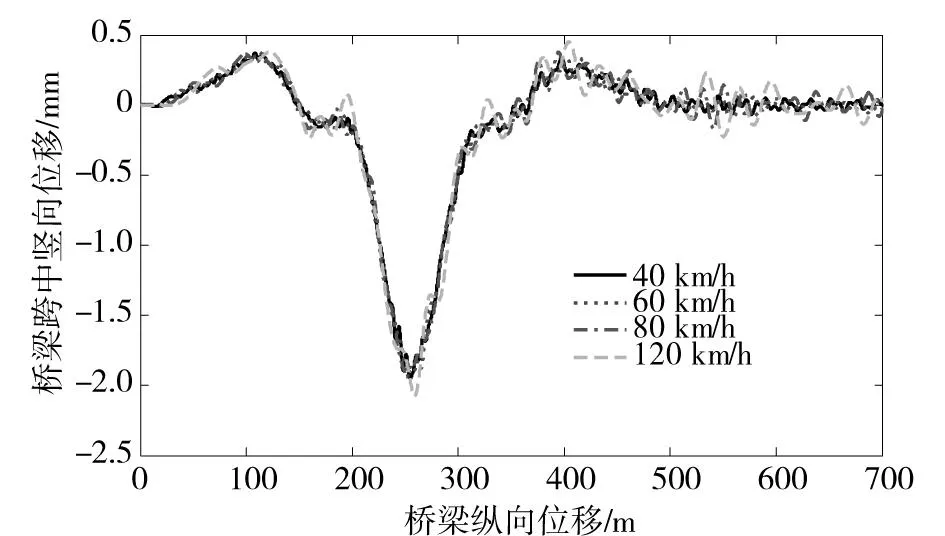
图6　桥梁跨中竖向位移随着桥梁纵向位移变化情况Fig.5 Vertical displacement at the middle of span vs the longitudinal displacement of the bridge

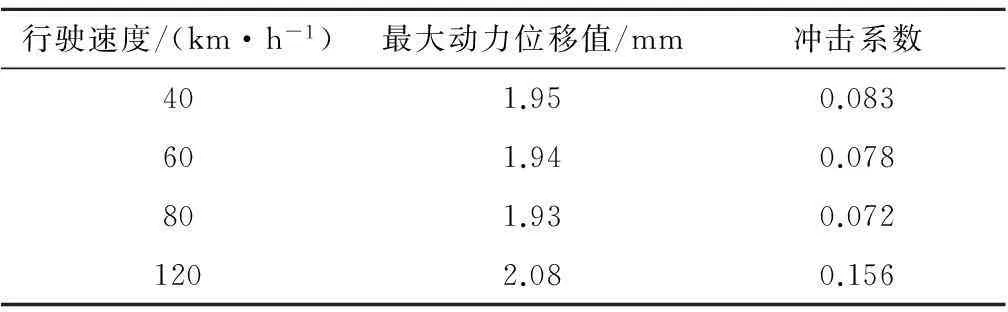
行驶速度/(km·h-1)最大动力位移值/mm冲击系数401.950.083601.940.078801.930.0721202.080.156

从图5和图6以及表3可以看出，桥梁的位移响应没有随着车速的增大而增大，当车辆经过桥梁跨中时，桥梁跨中位移达到最大值。车速由40 km/h增大到80 km/h时，跨中竖向位移最大值基本没有变化，当车速增大到120 km/h时，跨中竖向位移最大值增幅较大，通过研究表明，冲击系数并没有随着车速的增大而增大，而是随着车速的增大呈先减小后增大的规律。 因此，为了保证桥梁结构服役期间的安全性和行车舒适性应适当限制车辆过桥时的行驶速度。

3.2.3车辆数量的影响

为了研究桥上行驶的车辆数量对桥梁冲击系数的影响，分别取1辆、5辆、10辆和15辆二轴汽车对其进行计算分析，车辆行驶速度20 m/s，车辆前后间距为10 m，车辆距桥中心线的距离为10 m，路面粗糙度取为一般路面情况，为了考虑车辆的初始位移的影响，1辆车、5辆车、10辆车和15辆车的第1辆车的初始位置分别位于桥梁左侧200，300，400和500 m处。图7为桥梁跨中竖向位移随着时间变化的时程曲线，表4为不同数量的车辆行驶在桥上时跨中位置的最大动位移及冲击系数。

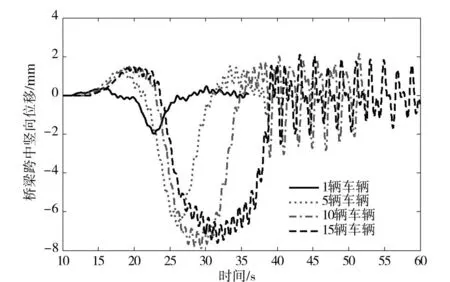
图7　桥梁跨中竖向位移时程Fig.7 Time history of the vertical displacement at the middle of the span

由图7可知，桥上车辆数量对桥梁跨中竖向位移响应有显著影响，当车辆数量由1辆增大到10辆时，主梁跨中竖向位移的最大值也随着车辆数量的增大而显著增大，但当车辆增大到15辆时，主梁跨中竖向位移的最大值反而较10辆时主梁跨中竖向位移的最大值要小。这可能是由于虽然15辆车辆同时作用在跨中但是位于跨中竖向影响线的不同符号的位置处，故导致主梁跨中竖向位移的最大值反而小于10辆车辆时的竖向位移最大值。

从表4可以看出，1辆车作用在桥上时冲击系数最大，车辆增加到5辆时冲击系数急剧减小，当车辆数增加到10辆时又有一定的增加，增加大15辆时又较10辆时有所减小，但仍比5辆车时的冲击系数大。因此，偏安全考虑计算冲击系数时应取1辆车辆进行计算分析。

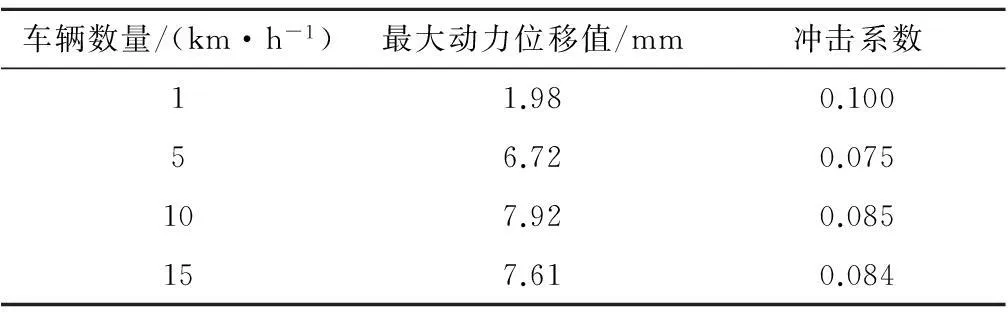
表4　跨中位置的最大动位移及冲击系数

3.2.4车辆间距的影响

为研究桥上行驶的车辆间距对桥梁和车辆动力响应的影响，取车辆数为5，行驶速度为20 m/s，车辆前后距离分别取5，10，20和30 m，车辆距桥中心线的距离为10 m，路面粗糙度取为一般路面情况，为了考虑车辆的初始位移的影响，对应于5，10，20和30 m前后距离的第1辆车的初始位置分别为位于桥梁左侧275，300，350和400 m处。图8为桥梁跨中竖向位移随着时间变化的时程曲线，表5为不同间距的5辆车行驶在桥上时跨中位置的最大动位移及冲击系数。

图8　桥梁跨中竖向位移时程Fig.8 Time history of vertical displacement at the middle of the span

从图8可以看出，车辆间距对桥梁位移响应时程曲线的幅值和形状基本都没有明显的影响。然而，从表5可以看出，车辆间距对冲击系数有一定影响，当车辆间距从5 m增大到30 m时冲击系数总体上呈微小上升趋势，当桥上有多辆车辆时，车辆间间距越大，冲击系数越大。故在桥梁实际运营期间应适当限制车辆的行驶间距以保证桥梁能够安全服役。

表5　跨中位置的最大动位移及冲击系数

4结论

1)路面状况越差，桥梁的动挠度围绕静挠度上下波动的幅度越大，最大动挠度随路况的恶化而增大，相应的冲击系数也变大。建议在桥梁服役期间要加强桥梁的养护，及时对桥面铺装层进行维护，这对于保证桥梁结构的安全性和行车舒适性意义重大。

2)桥梁的位移响应随着车速的增大变化不大，冲击系数随着车速的增大有先减小后增大的趋势。

3)桥上车辆数量对桥梁跨中竖向位移响应有显著影响，但变化规律不明显；桥上单独车辆时的冲击系数比多个车辆时的要大。

4)车辆间距对桥梁位移响应时程曲线的幅值和形状没有明显影响；车辆间距对冲击系数有一定影响，当桥上有多辆车辆时，车辆间距越大，冲击系数越大。建议在桥梁实际运营期间应适当限制车辆的行驶间距以保证桥梁能够安全服役。

参考文献：

[1] 许士杰. 钢管混凝土肋拱桥自振特性及汽车荷载作用下动力响应的研究 [D]. 北京：北方交通大学, 1999.

XU Shijie.On the basis of analyzing the mechanical characteristics of concrete filled steel tubular(CFST) arch bridges and the state-of-art of bridge vibration study [D]. Beijing: Beijing Jiaotong University, 1999.

[2] 李运生, 史莉莉, 王铮峰. 钢-混凝土简支组合箱梁桥在车辆荷载作用下的动力响应及冲击系数研究 [J]. 石家庄铁道大学学报(自然科学版), 2012, 25(1):7-13.

LI Yunsheng, SHI Lili, WANG Zhengfeng. Research on dynamic response and impact factor of simple steel-concrete composite box beam bridges under vehicle loads [J]. Journal of Shijiazhuang Tiedao University (Natural Science), 2012, 25(1):7-13.

[3] 袁明, 余钱华, 颜东煌. 基于车-桥系统耦合振动理论的大跨PC连续刚构桥冲击系数研究 [J]. 中国公路学报, 2008, 21(1):72-120.

YUAN Ming, YU Qianhua, YAN Donghuang.Research on impact coefficient for PC continuous rigid frame bridges with long-span under theory of vehicle-bridge system coupling vibration[J]. China Journal of Highway and Transport, 2008, 21(1):72-120.

[4] 许华东. 车辆作用下桥梁冲击系数分析 [J]. 重庆交通大学学报(自然科学版), 2013, 32(1):5-8.

XU Huadong. Analysis of bridge impact coeddicient with vehicles [J]. Journal of Chongqing Jiaotong University (Natural Science), 2013, 32(1):5-8.

[5] 桂水荣, 陈水生, 任永明. 先简支后连续梁桥车辆冲击系数影响因素研究 [J]. 公路交通科技,2011, 28(5):54-60.

GUI Shuirong, CHEN Shuisheng, REN Yongming. Research on influencing factors of impact coefficient of continuous beam bridge transformed from simply-supported structure subjected to moving vehicle loads [J]. Joumal of Highway and Transponation Research and Development, 2011, 28(5):54-60.

[6] 吴庆雄, 黄宛昆, 陈宝春. 中—下承式钢管混凝土拱桥车振调查与动力分析 [J]. 工程力学, 2013, 30(1):147-155.

WU Qingxiong, HUANG Wankun, CHEN Baochun.Vehicle-induced vibration research and dynamic analysis for concrete-filled steel tubular arch bridges [J]. Engineering Mechanics, 2013, 30(1):147-155.

[7] Dongzhou Huang. Vehicle-induced vibration of steel deck arch bridges and analytical methodology [J]. Journal of Bridge Engineering, 2012, 17(2):241-248.

[8] 孙潮, 吴庆雄, 陈宝春. 钢管混凝土拱桥车振性能分析 [J]. 公路交通科技, 2007, 24(12): 54-59.

SUN Chao, WU Qingxiong, CHEN Baochun. Analysis on dynamic behavior of concrete filled steel tubular arch bridge under vehicle moving loads [J]. Journal of Highway and Transportation Research and Development, 2007, 24(12): 54-59.

[9] 严志刚, 盛洪飞, 陈彦江. 桥面平整度对大跨度钢管混凝土拱桥车辆振动的影响 [J]. 中国公路学报, 2004, 17(4):41-44.

YAN Zhigang, SHENG Hongfei, CHEN Yanjiang.Effects of bridge deck roughness on vibration of long-span concrete filled steel tube arch bridges due to vehicles [J]. China Journal of Highway and Transport, 2004, 17(4):41-44.

[10] 李岩, 陈彦江, 黄新艺. 大跨异形钢管混凝土拱桥车载冲击效应分析 [J]. 哈尔滨工业大学学报, 2010, 42(1):109-114.

LI Yan, CHEN Yanjiang, HUANG Xinyi.Impact effect study on long-span irregular concrete filled steel tube arch bridge under moving vehicles [J]. Journal of Harbin Institute of Technology, 2010, 42(1):109-114.

[11] 陈灏, 陈水生. 下承式钢管混凝土系杆拱桥的冲击系数研究 [J]. 工程建设与设计， 2012(2)：117-121.

CHEN Hao, CHEN Shuisheng. Study on impact coefficient of under-supported CFST art bridge [J]. Engineering Gonstruction and Design, 2012(2): 117-121.

[12] JTGD60—2004,公路桥梁设计通用规范 [S].

JTGD60—2004, General code for desigh of highway bridges and culverts[S].

[13] Yan Han, C S Cai, Jianren Zhang, et al. Effects of aerodynamic parameters on the dynamic response of road vehicles and bridges under cross winds [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 134:78-95.

[14] Dodds C J, Robson J D. The description of road surface roughness [J]. Journal of Sound and Vibration, 1973, 31(2):175-183.

(编辑阳丽霞)

Research on the impact coefficientof the concrete filled steel tube arch bridge basedon the vehicle-bridge coupled vibration

HAN Yan, LI Hao, XUE Fanrong

(School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004, China)

Abstract:The three-dimensional finite element model of CFST arch bridge based on the software ANSYS was built and the dynamic characteristics of the structure were analyzed. Based on the vehicle-bridge coupled vibration model under the action of the two axle vehicle model, the self-made program for the vehicle-bridge coupled vibration analysiswas applied to calculate and analyze the effect of moving vehicles on the dynamic response of the CFST arch bridge considering the different the pavement roughness, different driving speed, different vehicle numbers and different driving distance of vehicle. Then, the impact coefficient of CFST arch bridge was calculated based on the vehicle-bridge coupled vibration. The research results show that the pavement roughness, driving speed of vehicle, the number of vehicles and the driving distance of vehicles have some effect on the impact coefficient of the CFST arch bridge. The conclusion obtained can provide a reference for the impact coefficient evaluation of CFST arch bridges at the design stage and the determining load effect for the bridge maintenance at the service stage.

Key words：CFST arch bridge; vehicle-bridge coupled vibration; finite element model; impact coefficient

中图分类号：U441+.3

文献标志码：A

文章编号：1672-7029(2016)03-0493-07

通讯作者：韩艳(1979—)，女，江苏连云港人，副教授，博士，从事桥梁抗风研究;E-mail:ce_hanyan@163.com

基金项目：国家自然科学基金资助项目(51278069)

收稿日期：2015-07-13