一种基于磁网络法的调制式磁齿轮计算模型

黎 曙，杨 高，祝后权

（武汉船用电力推进装置研究所，武汉 430064）



一种基于磁网络法的调制式磁齿轮计算模型

黎 曙，杨 高，祝后权

（武汉船用电力推进装置研究所，武汉 430064）

摘 要：文章提出调制式磁齿轮基于磁网络法的线性磁网络计算模型，对磁场进行求解分析，并应用于具体算例。通过对比分别由磁网络法与有限元法得到的磁密波形，表明该磁网络模型可有效应用于调制式磁齿轮磁场分析，在满足精度的同时可减少计算量，适合于工程设计与优化初选。

关键词：磁场调制式磁齿轮 磁场分析 磁网络法

0 引言

磁场调制式磁齿轮是一种新型的磁力传动机构。发展至今，以其高永磁利用率、高转矩密度[1]而广受关注，在水能发动机[2]、电力船舰推进器[3]、电力机车[4]、风能发电机[5]及磁力耦合传动等领域具有广阔的应用前景。

调制式磁齿轮内部的合成气隙磁场是决定磁齿轮性能的关键，众多学者对此展开研究。文献[6-7]提出调制式磁齿轮的解析计算方法，对内外气隙磁场进行计算；文献[8-9]利用有限元对调制式磁齿轮的齿槽定位转矩、参数优化、传输转矩等进行研究。但是解析计算精度上有较大误差，而有限元计算过程复杂，耗时久。为改善上述缺陷，文章采用磁网络法[10]研究调制式磁齿轮磁场。

本文构建调制式磁齿轮的线性磁网络模型，通过求解磁网络节点磁位方程获得内外气隙磁密分布曲线。并运用于具体算例，所得计算结果同有限元计算结果相比较，证实线性磁网络计算模型的有效性。

1 磁网络理论基础

磁网络法的依据是等效磁通管原理，即将所分析的场域中磁通分布较为均匀而几何形状又较为规则的部分作为一个独立的单元，计算其磁阻。各单元之间通过节点相连接，得到磁网络模型。

在建立磁网络模型前，把整个分析场域划分为有源区域和无源区域[11]。在有源区域，每个单元是由磁阻支路和等效磁势源串联而成，其中，等效磁势源用来等效永磁体的作用；在无源区域，每个单元就是一条磁阻支路。由此可知，磁网络模型中有两种不同性质的单元，即等效磁势源和等效磁阻。

1.1等效磁势源

在调制式磁齿轮当中，永磁体作为能量的供应者，大都采用钕铁硼永磁材料。钕铁硼永磁材料的退磁曲线基本上是一条直线，永磁体的工作点始终处于退磁曲线上，而且所用到的瓦形永磁体磁化均匀，故而可以认为永磁体内部磁密相等。恒定磁势源计算公式[12]为

其中， Hc为永磁体矫顽力；hm为永磁体充磁方向长度。

1.2等效磁阻

考虑材料存在磁饱和效应，等效磁阻有线性磁阻与非线性磁阻两种：

1）线性磁阻，包括永磁体磁阻、气隙磁阻和调磁块磁阻，它们不受磁饱和效应的影响，仅由调制式磁齿轮的结构尺寸决定。

线性磁阻单元具有固定几何形状而且磁导率不变。根据线性磁阻的定义，这类磁阻为：

其中，Ri表示单元磁阻；li表示单元的长度；Si表示单元的截面积；μ表示单元的绝对磁导率。

2）非线性磁阻，包括转子轭部磁阻，它们除了与调制式磁齿轮的结构尺寸有关外，还受磁饱和程度的影响。

在针对调制式磁齿轮的气隙磁场进行求解计算时，可将永磁体磁势视为求解区域的外部激励源，而区域内部单纯由线性磁阻构成。

2 磁网络模型的建立与求解

2.1磁网络方程的建立

在调制式磁齿轮的磁网络分析中，为了简化计算，做以下假设和处理：

1）忽略位移电流，即电磁场是似稳场；

2）磁场沿轴向不变，磁齿轮内部磁场退化二维平行平面场；

3）忽略铁磁材料的磁滞、涡流效应；

4）忽略电导率σ和磁导率μ的温度效应；

考虑到调制式磁齿轮旋转体的特性，可将其分为外永磁体环、外气隙环、调磁环、内气隙环和内永磁体环五个圆环区域，如图1所示。然后根据精度需要，将每个圆环区域划分成单层圆环或多层圆环。每层圆环由众多扇形环单元首尾连接所得。

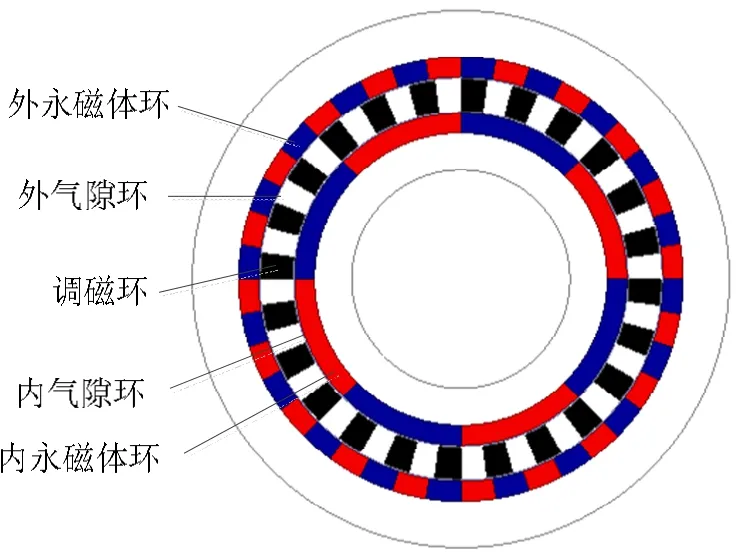
图1 调制式磁齿轮结构示意图

在每一个扇形环单元之中，大多数情况下，磁通的路线并不是一维的，往往在径向和周向上都有分布。为正确描述单元等效磁阻，对单元建立二维磁阻十字模型，如图2所示。图中R1、R4表示单元圆周方向的磁阻，R2、R3为表示单元径向磁阻，φi为各端线磁通，Fi为各端子磁势（i=1,2,3,4）。

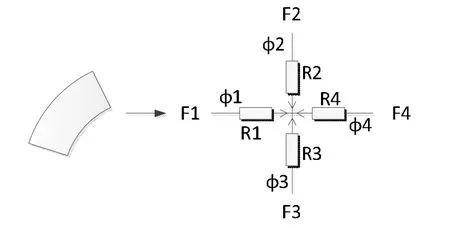
图2 扇形环单元磁网络模型

对于扇形环单元而言，我们关心的仅是其端变量，而并不需要了解其内部的场量，参考电网络的分析处理[13]，把这样具有4个引出端的扇形环单元视为一个4端网络，利用网络函数来表示端线磁势、磁通间的关系。

其中Y0为单元磁导矩阵。

通过端子压缩与端子消除，实现单元的环内连接（如图3所示）和环间连接（如图4所示），建立调制式磁齿轮整体的多端网络，由此获得调制式磁齿轮磁网络的三种节点磁位方程

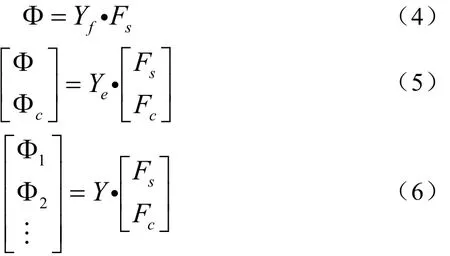
其中，方程（4）为连接点处既进行端子压缩又进行端子消除后所得节点磁位方程；方程（5）为连接点处只进行端子压缩后所得节点磁位方程；方程（6）为连接点处既未进行端子压缩又未进行端子消除后所得节点磁位方程。Yf、Ye、Y分别为对应的磁导矩阵。

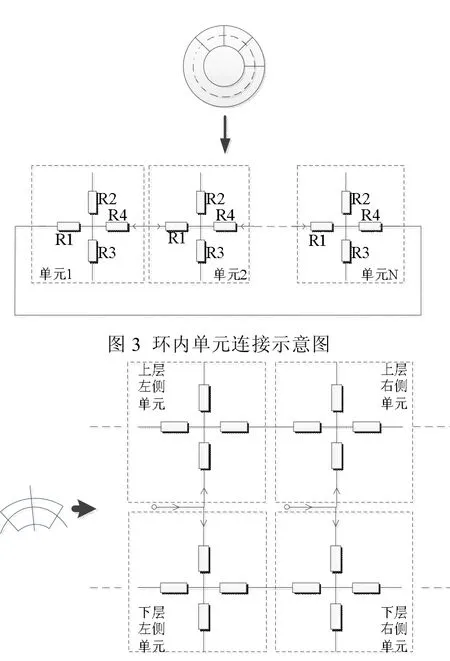
图4 环间单元连接示意图

2.2磁网络方程的求解

磁网络方程的求解分两步实现。先进行环间求解，将整体节点磁位方程拆分为各个单环节点磁位方程，再进行环内求解。利用已算得的各支路磁通及节点磁位逐步求解未知的支路磁通及节点磁位，直至算得所有支路磁通及节点磁位。求解流程图如图5所示。

通过求解磁网络方程，得到各气隙单元径向磁通，对应的径向磁密为

式中，Lθ为单元的周向宽度；W为单元的轴向长度；φri为各气隙单元径向磁通。根据求得的不同位置处的径向磁密值，可画出相应的径向磁密分布曲线。

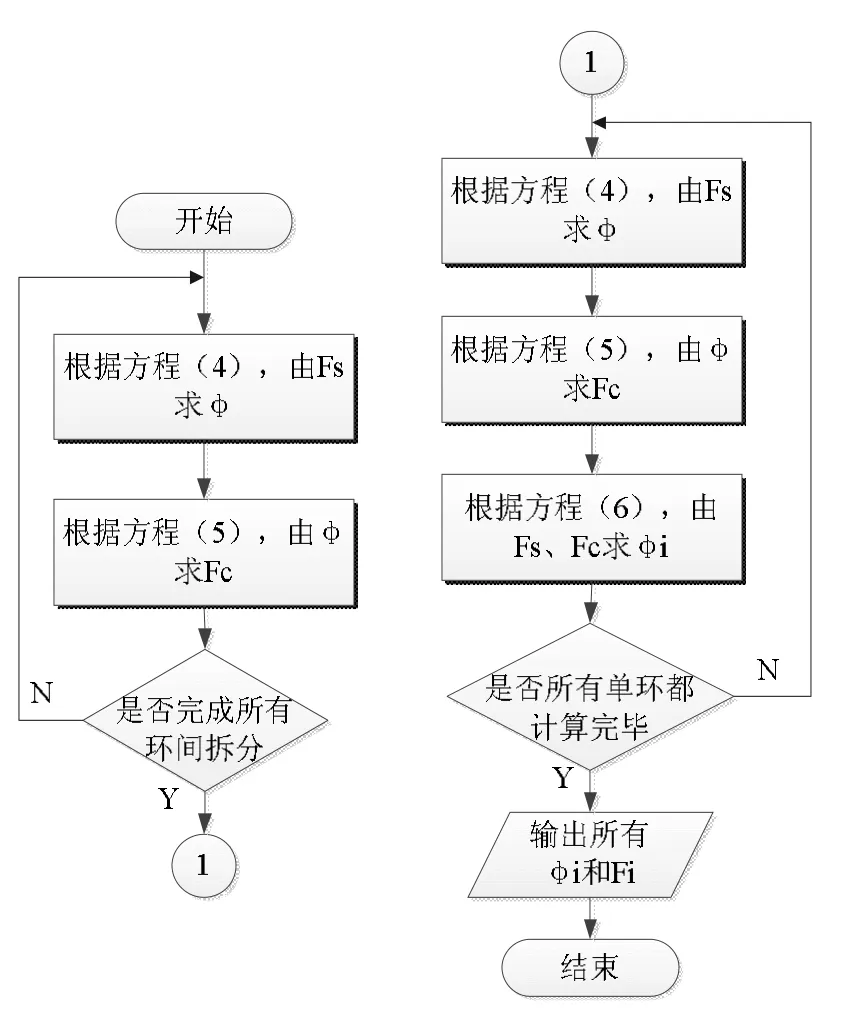
图5 磁网络节点磁位方程求解流程图

3 调制式磁齿轮磁场分析实例

运用所建立的调制式磁齿轮线性磁网络模型计算其内外气隙径向磁密。模型中各个圆环区域仅划分一层，每个单层环有240个单元，总计1200个单元，1440个运算节点，建立节点磁位方程进行求解。在有限元运算中，采用全模型进行求解，网格的划分采用默认的划分参数，总计2744个单元，求解参数也为系统默认。所用调制式磁齿轮的结构参数如表1所示。

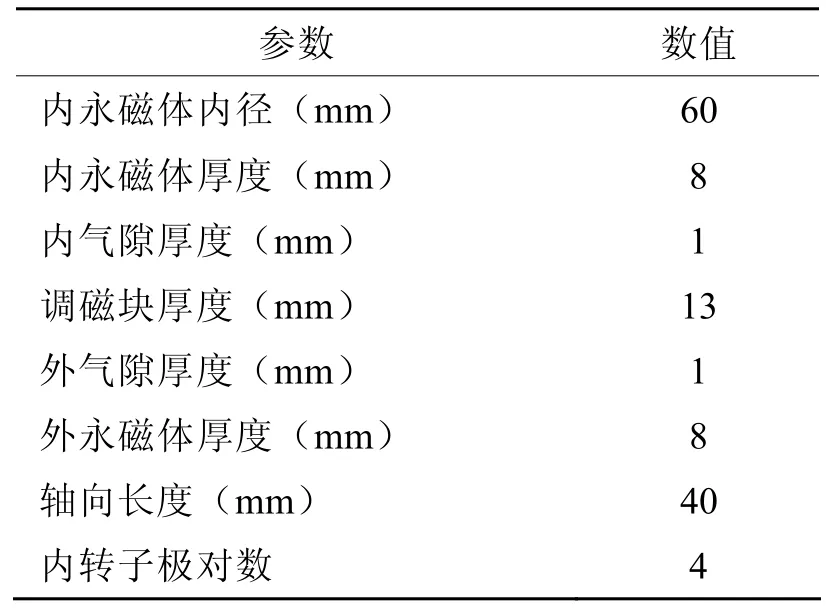
表1 调制式磁齿轮的结构参数表

外转子极对数 　20调磁块个数 　24调磁块绝对磁导率（H/m） 　50.52*10-4永磁体型号（径向充磁） 　NdFeB42M

3.1径向磁密曲线结果

内永磁转子经调磁环作用在外气隙处径向磁密分布曲线如图6所示，其傅立叶分解如图7所示，起关键作用的基波幅值与p1,-1次谐波[14]幅值如表2所示。

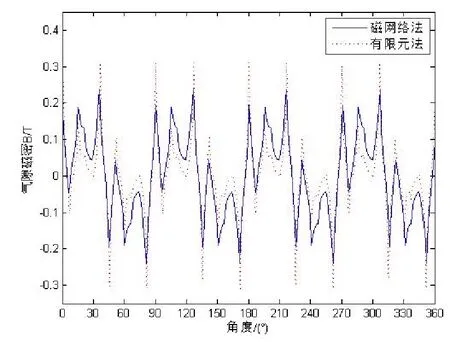
图6 内永磁体在外气隙处径向磁密分布曲线

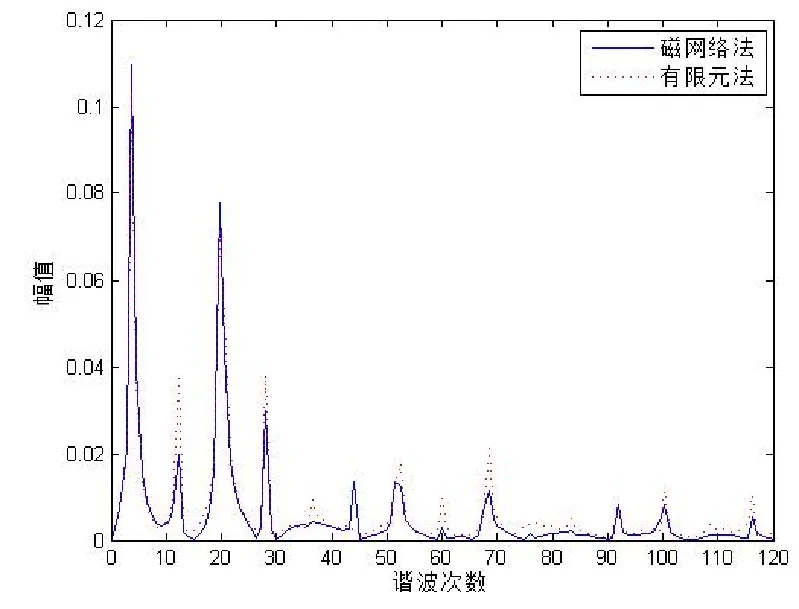
图7 内永磁体在外气隙处径向磁密波形的傅立叶分解

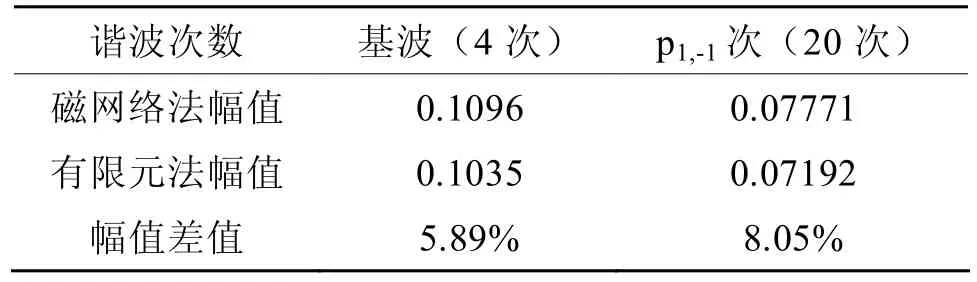
表2 内永磁体在外气隙处径向磁密谐波幅值表

外永磁转子经调磁环作用在内气隙处径向磁密分布曲线如图8所示，其傅立叶分解如图9所示，基波幅值与p1,-1次谐波幅值如表3所示。

3.2结果分析

由图6、图8可以看出，通过磁网络法计算所得气隙磁密分布曲线与有限元计算结果非常接近。而且通过图7、图9所示磁密分布波形的傅立叶分解的对比可以看出，两者方法算得的气隙磁密波形的各谐波成分近乎一致，仅极少数次谐波幅值有较大差异。而且，除基波与p1,-1次谐波外，其它各次谐波磁场的谐波幅值相对较小。又根据表2、表3可知，两种方法各自算得的气隙磁场中永磁体的基波与p1,-1次谐波幅值误差并不大，能够满足计算精度要求。

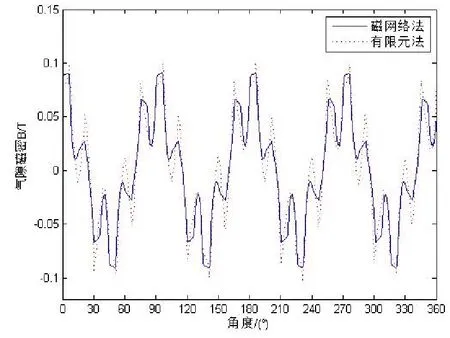
图8 外永磁体在内气隙处径向磁密分布曲线

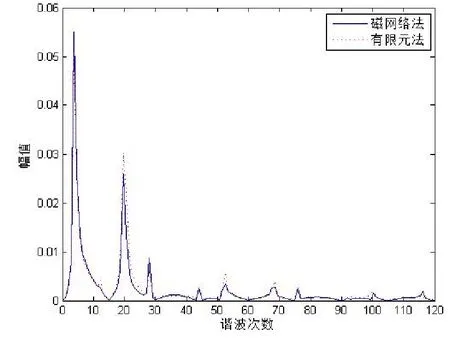
图9 外永磁体在内气隙处径向磁密波形的傅立叶分解

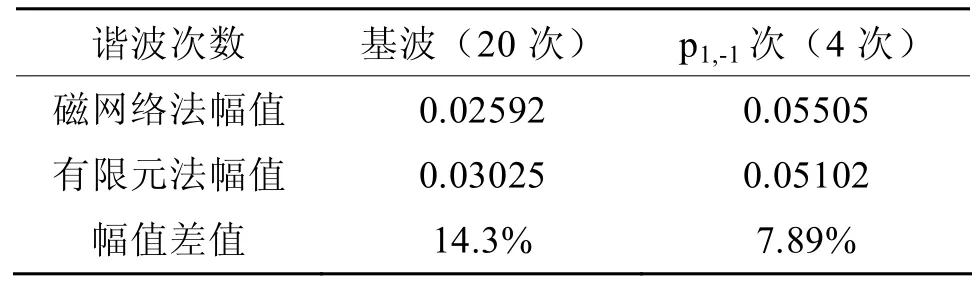
表3 外永磁体在内气隙处径向磁密谐波幅值表

4 结论

该线性磁网络计算模型可有效应用于调制式磁齿轮磁场分析。与有限元分析相比，在可获得足够的计算精度的同时，可大大减少了磁位方程组的节点数，减少计算量，可应用于工程设计与优化初选。

参考文献：

[1]K.Atallah,D.Howe.A novel high-performance magnetic gear[J].IEEE Transactions on Magnetics.2001,37(4):2844-2846.

[2]Laxman Shah,A.Cruden,Barry W.Williams.Amagnetic gear box for application with A contra-rotating tidal turbine[C].Proc.IEEE 7th Int.Conf.on Power Electronics and Drive Systems.PEDS’07,Nov.2007,pp.989-993.

[3]Nicolas W.Frank,Hamid A.Toliyat.Gearing ratios of a magnetic gear for marine applications[C].Proc.IEEE Conf.on Electric Ship Technologies Symposium.ESTS2009,Apr 2009,pp.477-481.

[4]K.T.Chau,Dong Zhang,J.Z.Jiang,et al.Design of a magnetic-geared outer-rotor permanent-magnet brushless motor for electric vehicles.IEEE Transactions on Magnetics.2007,43 (6):2504-2506.

[5]Linni Jian,K.T.Chau,J.Z.Jiang.A magnetic-geared outer-rotor permanent magnet brushless machine for wind power generation.IEEE On Industry Applications.2000,45(3):954-962.

[6]L.Jian,K.T.Chau.Analytical calculation of magnetic field distribution in coaxial magnetic gears[J].Progress in Electromagnetics Research.PIER,Vol.92,2009,pp.1-16.

[7]Thierry Lubin,Smail Mezani,Abderrezak Rezzoug.Analytical Computation of the Magnetic Field Distribution in a Magnetic Gear[J].IEEE Trans.Magn.2010,46(7):2611-2621.

[8]Zhu.Z.Q,Howe.D.Influence of design parameters on cogging torque in permanent magnet machines[J].IEEE Transactions on Energy Conversion.2000,15(4):407-412.

[9]Jian.L,Chau.K.T,Gong Y,et al.Comparison of coaxial magnetic gears with different topologies[J].IEEE Transactions on Magnetics.2009,45(10):4526-4529.

[10]Ostovic V.Dynamics of saturated electric machines.New York:Springer-Verlag,1989.

[11]樊叔维.电磁场数值计算方法——等效磁网络方法中参数的求解[J].光学精密工程.1999,7(3):23-27.

[12]王秀和.永磁电机（第二版）[M].北京:中国电力出版社,2010.

[13]吴宁.电网络分析与综合[M].北京:科学出版社,2003.

[14]刘新华.新型磁场调制式磁性齿轮的设计研究 [博士论文].上海:上海大学,2008年6月.

Research on the Magnetic Field of Field Modulated Permanent Magnetic Gear Based on Magnetic Network Method

Li Shu,Yang Gao,Zhu Houquan
(Wuhan Institute of Marine Electric Propulsion,CSIC,Wuhan 430064,China)

Abstract：This paper presents a linear mathematic model of FMPMG by using MNM and analyses the magnetic field.Through the comparisons of the magnetic flux density waveforms which calculated by MNM and FEM respectively,the results verify the efficiency of the computational model,which meets the accuracy needs and demands much less calculation,and is suitable for engineering design and the optimization of primaries.

Keywords：Field Modulated Permanent Magnetic Gear (FMPMG); analysis of magnetic field; Magnetic Network Method (MNM)

作者简介：黎曙(1991-)，男，硕士研究生。研究方向：永磁电机及其控制技术研究。

基金项目：湖北省科技支撑计划 2014BAA021

收稿日期：2015-11-23

中图分类号：TM351

文献标识码：A

文章编号：1003-4862（2016）02-0013-05