应用FAHP确定网络课程评价指标权重

李莉莉

摘 要： 针对网络课程评价的复杂性，在建立网络课程评价指标体系的基础上，引入模糊层次分析法确定网络课程评价指标权重，并给出了具体步骤。该方法根据三角模糊数比较大小的原理，采用定性和定量评价相结合的方式确定网络课程评价指标权重，既克服了专家评判时人为影响大的因素，使结果更加客观、科学，又易于编程和实现，具有很强的可操作性。

关键词： 网络课程； 三角模糊数； 模糊层次分析法； 评价指标

中图分类号：G434 文献标志码：A 文章编号：1006-8228（2016）04-55-03

Determining the evaluation index weight of Web-based course with FAHP

Li Lili

（Fuxin Higher Vocational College， Fuxin， Liaoning 123000， China）

Abstract： Due to the complexity of Web-based course evaluation， on the basis of establishing evaluation index system of Web-based course， FAHP （Fuzzy Analytical Hierarchy Process） method is proposed to determine the weight of evaluation index， and the specific steps are given. According to triangular fuzzy numbers comparative theory， the qualitative and quantitative evaluation methods are combined to determine the evaluation index weight of Web-based course， the method not only overcomes the anthropogenic influence factors of expert judgment， so as to make the result more objective and scientific， but also is easy to program and realize， with strong operability.

Key words： Web-based course； triangular fuzzy number； fuzzy analytic hierarchy process （FAHP）； evaluation index

0 引言

随着信息技术的不断发展，网络课程突破了传统教学方式，越来越显示出其优越性和快捷性。如今，各种网络课程的质量良莠不齐，如何科学地评价网络课程、更好的规范网络课程发展，科学、客观地确定网络课程评价指标体系成为重点。在传统的网络课程评价中，通常是由专家根据以往的经验给出主观性的判断，其具有一定的模糊性。为了克服传统评价的缺陷，本文根据中国教育信息化技术标准CELTS-22《网络课程评价规范》确定的指标体系[1]，在网络课程评价中引入模糊层次分析法（Fuzzy AHP，简称FAHP），并利用三角模糊数比较大小求出元素排序的方法，来确定网络课程评价指标权重，使评价结果更加客观、科学。

1 三角模糊数原理

定义1 三角模糊数可以通过其隶属度函数定义如下[2]：

⑴

式中，l≤m≤u，l和u分别代表判断的模糊程度。

设三角模糊数分别为，，，则其计算法则为[3]：

⑵

⑶

⑷

⑸

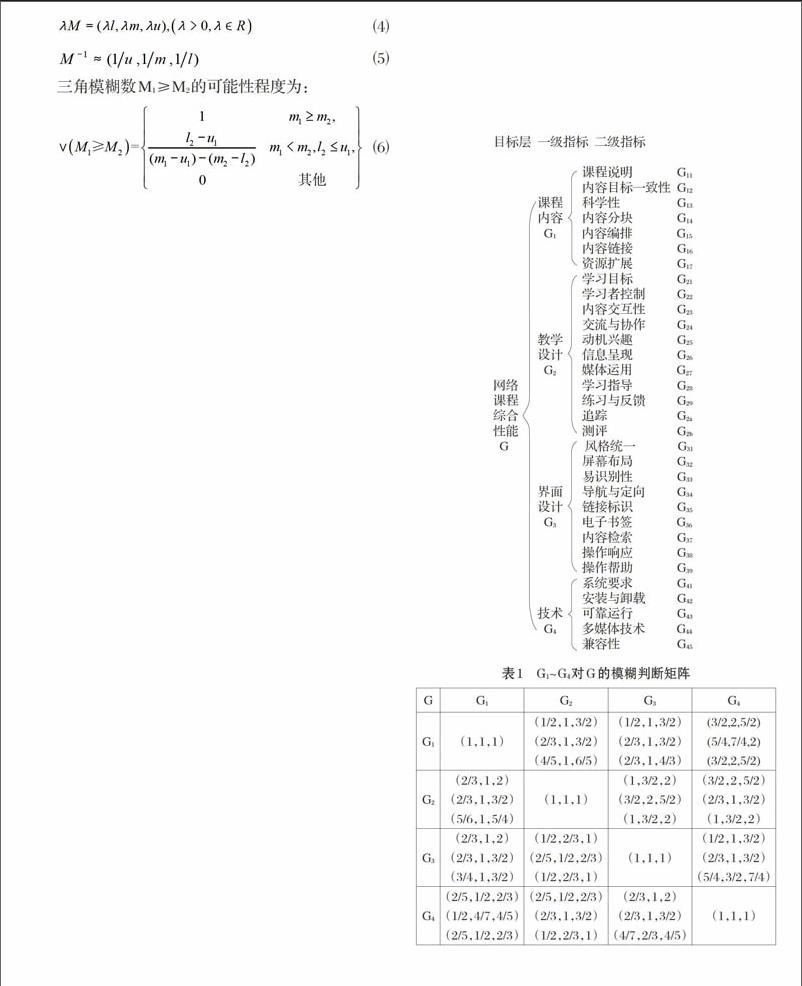
三角模糊数M1≥M2的可能性程度为：

⑹

2 应用模糊层析分析法确定网络课程评价指标权重过程

⑴ 根据问题的总目标，确定评价人员或小组，建立网络课程评价问题的系统递阶层次结构模型。

⑵ 由专家利用三角模糊数对网络课程评价指标进行两两比较，并构造模糊判断矩阵。对同一级别下的所有指标进行两两比较时，使用三角模糊数表示为：A=（aij）n×m，aij=[lij，mij，uij]，且aij==[1/uij，1/mij，i/lij]。当有T位专家进行评价时，aij为aij=1/T（++…+），其中为第t个专家进行评价时得出的三角模糊数[4]。

⑶ 对网络课程评价指标模糊判断矩阵中各个指标的综合重要程度值进行计算。

⑷ 对网络课程模糊判断矩阵进行层次单排序，计算出第i个元素Ai重要于其他各个元素的可能性程度，即d'（Ai）=（Si≥Sj）≥（i=1，2，…，n），由此计算出W'=（d'（A1），d'（A2），…，d'（An）T，最后将其作归一化处理，计算出权重向量W=（d（A1），d（A2），…，d（An））T。

⑸ 对网络课程评价指标进行层次总排序。总排序向量为评价指标相对于总目标的权重向量和评价对象相对于评价指标的权重矩阵的乘积。其中总排序向量下的各分量即为各评价对象在总目标下的权重[4]。

3 模糊层析分析法在确定网络课程评价指标权重中的具体应用

第一步，本文遵循中国教育信息化技术标准CELTS-22《网络课程评价规范》中所确定的指标体系，据此进行网络课程的综合评价[1]，确定递阶层次指标体系如图1所示。

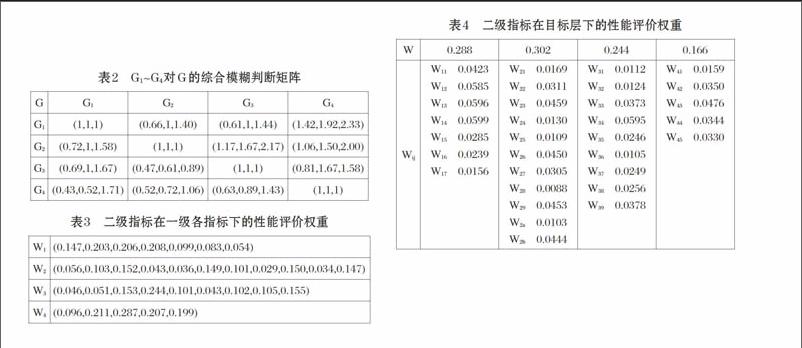
第二步，确定一级指标相对于目标层的权重。根据总目标的要求，由参加网络课程评价的专家（本文假设有三位专家）通过对各准则之间两两比较其重要性，可以构造出一级指标相对于目标层的三角模糊数判断矩阵。一级指标G1～G4相对于目标层G的模糊判断矩阵和综合模糊判断矩阵如表1和表2所示。由此再计算出一级指标相对于目标层的归一化权重向量为W=（0.288，0.302，0.244，0.166）。

第三步，确定二级指标相对于一级各指标的权重。其原理同上，因篇幅有限，在此不列出求取二级指标权重的三角模糊数判断矩阵、综合判断矩阵及其求解二级指标权重向量过程。二级指标相对于一级各指标的权重向量如表3所示。

第四步，确定二级指标相对于目标层的权重。根据上面计算出的一级指标相对于目标层的权重向量和二级指标相对于一级指标的各权重向量，可以计算出二级指标相对于目标层的各个权重，见表4。

4 结束语

进行网络课程评价最重要的是准确、科学地确定指标权重。本文引入模糊层次分析法以避免权重确定中人为打分的随意性，同时又能够用数学方法反映出人们思维模式的模糊性。该方法简单实用，易于编程实现，为网络课程指标权重的确定提供了一种新的方法和思路。

参考文献（References）：

[1] 中国教育信息化技术标准CELTS-22“网络课程评价规范”

[EB/OL].http：//www.celtsc.edu.cn，2006-4-3.

[2] 姜艳萍，樊治平.一种三角模糊数互补判断矩阵的排序方法[J].

系统工程与电子技术，2002.24（7）：34-36

[3] 费军.模糊层次分析法在审计固有风险评估中的应用[J].数

学的实践与认识，2005.35（12）：44-50

[4] 戢一鸣，张金隆.应用FAHP确定供应链绩效评价指标权重[J].

华中师范大学学报（自然科学版），2005.39（2）：190-194

[5] 刘秀琴.网络课程绩效综合评判[J].电化教育研究，2005.4：

74-76

[6] 陈东升，谭瑞梅，杨杰.网络课程的模糊综合评价[J].电化教育

研究，2005.12：42-45

[7] 李松，王彦梅.基于AHP的教师教学质量的模糊评判[J].中国

职业技术教育，2005.30：28-30

[8] 王建，黄凤岗，景韶光.AHP中判断矩阵一致性调整方法研究[J].

系统工程理论与实践，2005.8：85-91