基于Voronoi图和地面无人平台最优观测的目标跟踪研究
宋志强+周献中+李华雄


摘 要: 针对带防守区域约束的多地面无人平台(UGV)协同跟踪单目标问题,提出了基于多UGV最佳观测位置的目标跟踪算法。首先在无约束情况下,研究基于梯度法的UGV观测位置调整,然后添加约束条件,利用Voronoi图的相关特性,研究在UGV各自防守区域及速度等约束条件下的UGV观测位置优化问题,通过最小化数据融合后的协方差矩阵行列式,从而调整UGV的观测位置,来获得更好的跟踪质量。仿真结果表明了算法的有效性和合理性。
关键词: Voronoi图; 地面无人平台; 协同控制; 主动目标跟踪
中图分类号:TP11 文献标志码:A 文章编号:1006-8228(2016)04-17-04
Research on target tracking based on voronoi diagram and optimal
observation of unmanned ground vehicles
Song Zhiqiang1, Zhou Xianzhong2, Li Huaxiong2
(1. Institute of Electrical and Information Technology, Suzhou Institute of Trade & Commerce, Suzhou, Jiangsu 215009, China;
2. School of Management and Engineering, Nanjing University)
Abstract: For the problem of multiple unmanned ground vehicles (UGVs) with defense area constraints collaboratively tracking a single target, a target tracking algorithm is proposed based on the optimal observation position of UGVs. Firstly, in the unconstrained case the observation position adjustment of UGVs based on the gradient method is researched. Then the observation position optimization problem of UGVs with the constraints of UGV's defensive area and velocity is addressed using the characteristics of Voronoi diagram. The UGVs can adjust the observation position by minimizing the determinant of the fused covariance matrix and get better tracking quality. The simulation results showed the validity and rationality of the algorithm.
Key words: Voronoi diagram; unmanned ground vehicle; collaborative control; active target tracking
0 引言
地面无人平台(Unmanned Ground Vehicle,UGV)又名无人车,其在军事和民用领域都具有广泛的应用[1-3]。单个UGV在探测能力和信息获取方面有一定局限性,多UGV之间协同可以完成单平台不能完成的任务。本文主要研究多地面无人平台的部署问题,以最大化移动目标的位置估计准确性。多无人平台跟踪目标问题在监视、巡逻、环境监测等方面具有应用价值。对于静态传感器的目标跟踪已有较广泛的研究[4-6],相对于静态传感器,移动传感器在传感质量、区域覆盖、环境适应性等方面均具有优势,多移动传感器的协作传感可利用传感器的移动能力以提高目标跟踪性能[7-11]。文献[7-8]研究了跟踪目标时仅有距离测量的多移动传感器最优运动策略问题。文献[9-10]使用距离和方位测量,提出一种移动传感器近似跟踪策略以最小化目标的位置不确定性。文献[11]提出基于多无人机的主动目标跟踪与联合定位方法,采用卡尔曼滤波器估计目标位置。现有文献较少考虑各平台的运动约束,均没有考虑各平台的防守区域约束。本文考虑各平台的运动约束和平台防守区域约束,研究多UGV主动目标跟踪问题。
1 主动目标跟踪简介
1.1 基于Voronoi图的多UGV部署
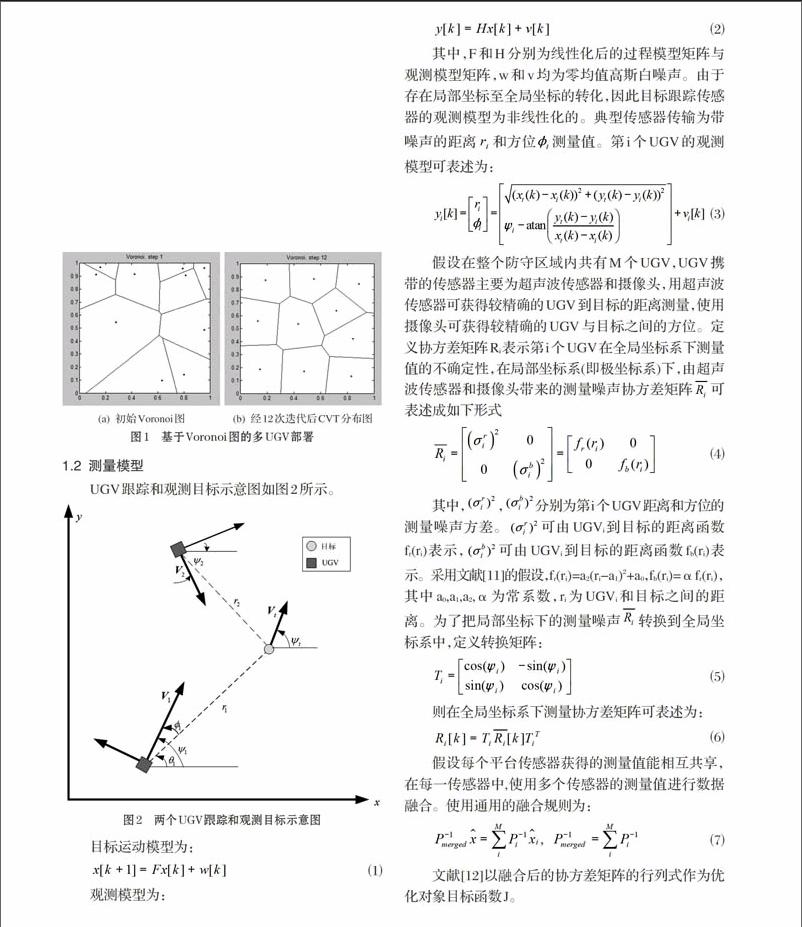
根据Voronoi图原理,各UGV可根据自身及周围其他UGV的位置信息来构造各自Voronoi多边形区域,再计算该区域质心位置,最后各UGV以各自区域质心为目的地,运动至该目的地,最终各UGV可形成更为稳定的质心Voronoi分布(CVT)。基于Voronoi图的多UGV部署如图1所示。从图1(a)和图1(b)的比较可以看出,CVT划分要比Voronoi划分更加均匀,可使各跟踪平台负担较为均衡。
1.2 测量模型
UGV跟踪和观测目标示意图如图2所示。
目标运动模型为:
⑴
观测模型为:
⑵
其中,F和H分别为线性化后的过程模型矩阵与观测模型矩阵,w和v均为零均值高斯白噪声。由于存在局部坐标至全局坐标的转化,因此目标跟踪传感器的观测模型为非线性化的。典型传感器传输为带噪声的距离和方位测量值。第i个UGV的观测模型可表述为:
⑶
假设在整个防守区域内共有M个UGV,UGV携带的传感器主要为超声波传感器和摄像头,用超声波传感器可获得较精确的UGV到目标的距离测量,使用摄像头可获得较精确的UGV与目标之间的方位。定义协方差矩阵Ri表示第i个UGV在全局坐标系下测量值的不确定性,在局部坐标系(即极坐标系)下,由超声波传感器和摄像头带来的测量噪声协方差矩阵可表述成如下形式
⑷
其中,,分别为第i个UGV距离和方位的测量噪声方差。可由UGVi到目标的距离函数fr(ri)表示,可由UGVi到目标的距离函数fb(ri)表示。采用文献[11]的假设,fr(ri)=a2(ri-a1)2+a0,fb(ri)=αfr(ri),其中a0,a1,a2,α为常系数,ri为UGVi和目标之间的距离。为了把局部坐标下的测量噪声转换到全局坐标系中,定义转换矩阵:
⑸
则在全局坐标系下测量协方差矩阵可表述为:
⑹
假设每个平台传感器获得的测量值能相互共享,在每一传感器中,使用多个传感器的测量值进行数据融合。使用通用的融合规则为:
⑺
文献[12]以融合后的协方差矩阵的行列式作为优化对象目标函数J。
⑻
2 协同控制律设计
我们采用梯度下降法最小化目标函数J。目标函数在极坐标下的梯度可表示为:
⑼
结合矩阵论相关知识:
⑽
⑾
⑿
可得:
⒀
其中,zi为ri或ψi。
证明:
对行列式求微分得
因此有:
所以有:
而在极坐标下,对Ri求偏导数可得:
于是可求得及。
UGV运动模型采用二阶积分模型[11]:
⒁
设计基于梯度的控制律为
⒂
其中,B?0,为阻尼矩阵。C?0,为增益矩阵。
3 协同目标跟踪算法描述
基于Voronoi图和UGV最优观测的目标跟踪算法如表1所示。
4 仿真研究
同时考虑UGV速度、角速度、防守区域约束,三个UGV协同跟踪一个目标时的跟踪效果如图3所示,仿真参数如表2所示。
表1 协调目标跟踪算法
[基于Voronoi图和UGV最优观测的目标跟踪算法\&Step 1:指挥中心根据各跟踪平台位置生成用于协同跟踪的Voronoi图;
Step 2:指挥中心根据当前战场态势,决定是否要生成质心Voronoi图;
Step 2.1:若当前态势不紧急,则指挥中心命令各跟踪平台运动至自身所在Voronoi区域的质心。
Step 2.2:若当前态势紧急,则各跟踪平台直接处于待命状态。
Step 3:在每个时间步k
//局部观测
Step 3.1:进行局部测量;
更新局部估计及误差协方差矩阵Pi;
//传感器融合
Step 3.2:向其他平台发送局部信息;
接收来自其他平台的局部信息(其他平台也可能返回空信息,即其他平台还没有探测到目标);融合所有局部估计(也有可能只有当前跟踪平台的估计)得到全局估计和全局误差协方差矩阵P;
//优化平台/传感器位置
Step 3.3:使用目标函数的梯度产生平台下一步的最优位置;
//更新位置
Step 3.4:跟踪平台移动至期望的位置(需考虑UGV的运动约束)。对于仅有当前主跟踪平台探测到目标而其他邻近平台尚未探测到目标的情况,当前主跟踪平台仍运动到下一步的最优位置,且当前跟踪平台命令邻居平台向目标移动。
Step 4:当目标接近Voronoi多边形边界时,当前主跟踪平台若收到来自邻近平台的测量估计,则进入准备阶段,当目标越过Voronoi边进入下一个Voronoi区域时,该区域的跟踪平台切换为当前主跟踪平台,前一时刻的主跟踪平台切换为从跟踪平台。
Step 5:各跟踪平台的运动不超过其自身防卫区域。对当前没有探测到入侵目标的平台,在其所有邻域平台失去跟踪目标后,返回Voronoi区域的质心位置,即原位置。\&]
图3 有防守区域约束时的UGV协同目标跟踪示意图
表2 仿真参数
[参数\&参数值\&说明\&T\&0.1 s\&采样周期\&vmax\&5.0 m/s\&UGV最大速度\&ωmax\&0.30 rad/s\&UGV最大角速度\&a2\&0.0008\&传感器相关常系数\&a1\&15.625\&传感器相关常系数\&a0\&0.1528\&传感器相关常系数\&a\&5\&传感器相关常系数\&]
由图3可知,刚开始时,三个UGV协同跟踪目标,当UGV 2即将到达Voronoi多边形边界时,停止前行,保证UGV 2不离开自身防守区域,而其他UGV则继续对目标进行跟踪。基于Voronoi图的多UGV协同目标跟踪算法使得各UGV在不离开各自防守区域的前提下,实现对目标的最优观测。
5 结束语
本文基于目标运动模型和传感器观测模型,提出基于UGV最佳观测位置的协同目标跟踪方法。首先对于无约束情况,研究基于梯度法的UGV观测位置调整,然后添加约束条件,利用Voronoi图的相关特性,研究在UGV各自防守区域及速度等约束条件的UGV观测位置优化问题,通过最小化数据融合后的协方差矩阵行列式调整UGV的观测位置,来获得更好的跟踪质量。仿真结果表明了该控制算法的有效性。
后期研究拟针对UGV实物,将设计的控制算法在UGV实物平台上测试、运行,以检验算法的实用性并进一步优化算法。
参考文献(References):
[1] Nigam N, Bieniawski S, Kroo I, et al. Control of Multiple
UAVs for Persistent Surveillance: Algorithm and Flight Test Results[J].IEEE Transactions on Control Systems Technology,2012.20(5):1236-1251
[2] Forsmo E. J., Grotli E. I., Fossen T. I., et.al. Optimal
search mission with Unmanned Aerial Vehicles using Mixed Integer Linear Programming[C]//2013 International Conference on Unmanned Aircraft Systems (ICUAS). IEEE,2013:253-259
[3] Acebedo J J, Arrue B C, Maza I, et al. Cooperative Large
Area Surveillance with a Team of Aerial Mobile Robots for Long Endurance Missions[J]. Journal of Intelligent & Robotic Systems Theory & Applications,2013.70(14):329-346
[4] Bar-Shalom Y, Kirubarajan T, Li X R. Estimation with
Applications to Tracking and Navigation[M].New York: Wiley,2001.
[5] Dariusz U, Optimal Measurement Methods for Distributed
Parameter System Identification[M]. Boca Raton, FL: CRC,2004.
[6] Taylor C, Rahimi A, Bachrach J, et al. Simultaneous
localization, calibration, and tracking in an ad hoc sensor network[C]// In IPSN '06: Proceedings of the fifth international conference on Information processing in sensor networks,2006:27-33
[7] Zhou K, Roumeliotis S I. Optimal motion strategies for
range-only constrained multisensor target tracking[J]. IEEE Transactions on Robotics,2008.24(5):1168-1185
[8] Stump E, Kumar V, Grocholsky B, et al. Control for
localization of targets using range-only sensors[J]. Int. J. Robot. Res,2009.28(6):743-757
[9] Stroupe A W, Balch T. Value-based action selection for
observation with robot teams using probabilistic techniques[J].Robotics & Autonomous Systems,2005.50(2-3):85-97
[10] Zhou K, Roumeliotis S I. Multi-robot active target
tracking with combinations of relative observations[J]. Robotics IEEE Transactions on,2010.27(4):678-695
[11] Morbidi F, Mariottini G L. Active target tracking and
cooperative localization for teams of aerial vehicles[J]. IEEE Transactions on Control Systems Technology,2013.21(5):1694-1707
[12] Chung T H, Burdick J W, Murray R M. A decentralized
motion coordination strategy for dynamic target tracking[C]//2006 IEEE International Conference on Robotics and Automation(ICRA 2006). IEEE,2006:2416-2422

