基于模糊理论的城市道路短时交通流量预测研究
黄慧琼
(广西科技大学 汽车与交通学院, 广西 柳州 545006)
基于模糊理论的城市道路短时交通流量预测研究
黄慧琼
(广西科技大学 汽车与交通学院, 广西 柳州545006)
[摘要]交通信息分析与处理是实现智能交通系统的有力环节,而交通流量预测是其重要研究内容。在现有研究基础上,以及考虑到交通量时变、复杂特性,提出了基于模糊线性回归的道路交通流量的预测模型,为实现交通诱导与管理控制等方案实施提供理论依据,也为驾驶员和管理者提供决策支持。通过实地采集的交通流量数据进行实证研究,并与多元线性回归预测结果进行对比分析。结果表明了基于模糊线性回归的预测结果总体效果要好,在实际交通流量预测中发挥着重要作用。
[关键词]交通流量; 模糊理论; 模糊线性回归; 流量预测
1概述
交通信息分析与处理在交通管理与控制中占据重要地位,交通流量预测又是交通信息分析与处理重要研究内容之一。其中,对城市道路交通流量预测是实现智能交通管理不可或缺的部分,其预测的结果能为交通诱导与管理控制的方案制定提供支持[1]。同时,也方便出行者选择最佳出行路线以避开交通拥挤路段,提高道路的通行能力和服务水平[2]。因此,对交通流量短时预测方法的研究至关重要,在先进的智能交通系统(ITS)中发挥着重要作用,也是近些年国内外学者研究的重点问题之一[3]。
本文在现有交通流量预测模型的基础上,研究了将模糊理论引入到交通信息处理技术中去,努力为交通流量预测找到新的方法。考虑到道路交通流量预测结果与交通诱导与控制方案的实施息息相关,其预测结果的好坏很大程度上制约着决策的客观时效性,又因为交通流具有复杂、时变特性,而模糊线性回归算法具有分析复杂系统的特点,且有算法简单、求解快速等特定。因此,本文运用模糊线性回归算法对交通流量的预测进行建模,应用柳州市城中区文昌路路段实际采集的交通流量数据对模型预测结果进行实证研究。将预测结果与真实值进行对比分析。结果表明其预测交通量真实可靠,能为交通管理者或出行者提供决策支持,而且有效地避免因使用历史交通数据而制定出不合理的出行方案[4]。另外,采用STPS软件对交通流量数据进行线性回归,并与文中建立的模糊线性回归结果进行对比,从对比结果可得出后者预测模型实用性很强。
2基于模糊线性回归的交通流量预测
早期的交通流量预测模型主要有自回归滑动平均模型(ARMA)[5]、自回归模型(AR)[6]、滑动平均模型(MA)[7]和历史平均模型(HA)[8]等等。这些模型虽然存在建模方便、计算简单以及易于更新数据等特点,但对于交通流过程中出行的随机性与非线性则表现出模型的较差的泛化能力和鲁棒性。通常会随着预测时间间隔的缩短,这些模型的预测精度会受到很大程度的影响[9]。
随着交通量预测研究的快速发展,学者们相继提出了一些新的预测模型,其预测精度相比之前的有了很大的提高。主要有多元线性回归模型、ARIMA模型、自适应权重联合模型、Kalman滤波模型、BP神经网络、最小二乘法拟合等模型与算法,但这些算法或多或少都存在一定的缺陷[10]。本文重点研究了基于模糊线性回归预测模型对交通流量进行预测,并给出实例验证。模糊线性回归预测求解主要按以下基本步骤进行:
① 首先对预测对象相关因素进行分析,并提取主要有关特征进行分析,找到预测因素(因变量)和影响预测结果的因素(自变量)。
② 运用交通调查与分析方法实地调查交通流量数据,或选取历史交通流量数据,选择合适数学方法建模,应用一定的方法建立模糊回归预测模型。
③ 利用回归预测模型进行预测,并得到预测结果。
④ 分析、评价回归预测结果的精确度和可靠性。
模糊线性回归模型:
设有观测值

x11x12…x1ny1x21x22…x2ny2……………xm1xm2…xmnyn,
其中xi1,xi2,…,xin为输入,yi为输出,i=1,2,…m,首先对输出数据进行模糊化,使对应yi模糊输出为Yi为模糊数Yi(yi,ei),(i=1,2,…,m),其中ei根据实际问题而定[11]。

当C>0时,
(1)
当C=0时,
(2)

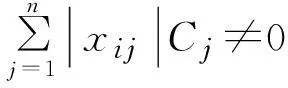
(3)
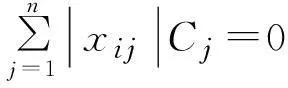
(4)
该模型的确定在于参数a1,a2…aj及C1,C2…Cj的确定,首先确定拟和度与模糊度。

(5)
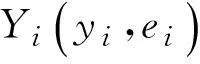
(6)

根据糊线性回归求解的中心思想,将模糊回归模型问题求解转为在满足一定约束条件下,以使得预测变量模糊度最小为目标的线性规划问题[12]。根据上述分析可知,模糊线性规划问题转化为求解下列线性规划问题[13]:
(7)
其中:H是事先给定的。由上述关于hi的公式,上述线性规划问题为:
(8)
3实证研究
3.1数据来源
为了验证上述模型和方法,预测实例所采用的数据来源于柳州市城中区文昌路(文昌路与东环路交叉口)2014年11月5日、12日、19日及26日的实测交通流量数据。以每5 min为交通调查间隔,共30组数据。取文昌路11月5日—26日的08:00—10:30时刻流量,主要包括小汽车和客车的流量,流量曲线见图1。考虑篇幅,具体数据未列出。
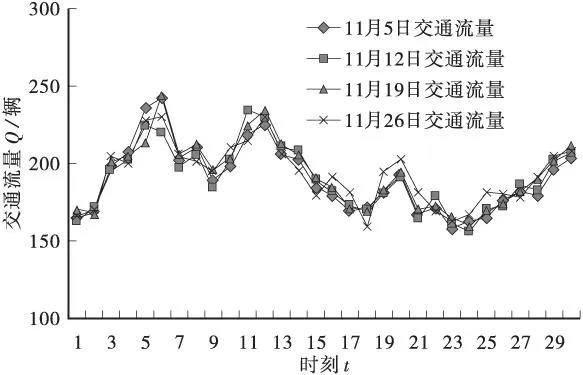
图1 文昌路段交叉口交通流量曲线Figure 1 Traffic flow curve of the wenchang road intersection
3.2模型线性回归预测模型建立与求解
根据图1所示的交通流量曲线,以文昌路路段前3周(5日、12日、19日)t时刻的流量q1,q2,q3为自变量,建立与文昌路26日t时刻流量(因变量)的模糊线性回归方程。
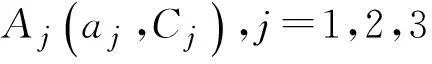
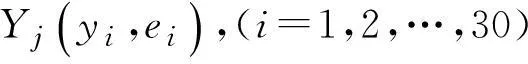
根据常用的模糊线性回归权重选择原则:
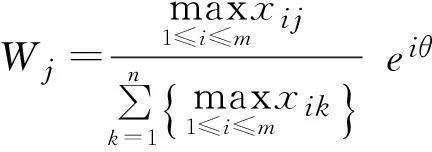
计算得到W1=0.337 5,W2=0.320 7,W3=0.341 7。
则S=0.337 5C1+0.320 7C2+0.341 7C3。
则求解参数问题可以转化为求解下列线性规划问题:
(9)
根据式(9),则完整的模糊回归预测模型转化成线性规划方程为:
(10)
将表1的数据代入式(10),借助Matlab数学软件,计算得到:
(a1,C1)=(-0.176,0),
(a2,C2)=(0.238,0.138),
(a3,C3)=(0.945,0)。
3.3基于STPS多元线性回归流量预测结果
同样采用上述图1的实测交通流量数据,以11月26日t时文昌路交通流量为因变量,其它3个数据为自变量,构造多元线性回归方程,应用STPS软件进行回归分析,得到一下基本信息。
模型拟合度分析:
从表1中数据可以看出:模型拟合度R=93.5%,说明可以用线性回归模型来预测结果。

表1 模型汇总Table1 Themodelsummary模型RR方调整R方标准估计的误差10.935a0.8740.8597.43307 a.预测变量:(常量),VAR00004,VAR00002,VAR00003;b.因变量:VAR00001。
显著性分析:
从表2中数据可以看出:Sig=0.000<0.005,说明该模型非常显著,可信。表3为模型系数。

表2 显著性分析Table2 Significantanalysis模型平方和df均方FSig.1回归9948.28533316.09560.0190.000a残差1436.5152655.251总计11384.80029

表3 模型系数Table3 Coefficientofthemodel模型非标准化系数标准系数B标准误差试用版tSig.1(常量)29.70512.5992.3580.026VAR000050.3580.2610.4011.3700.182VAR000060.0500.2360.0540.2130.833VAR000070.4440.2730.4901.6260.116
因此,回归分析结果如下:
Y=29.705+0.358x1+0.050x2+0.444x3
(11)
4结果对比与分析
基于线性模回归各拟合的中心值与观测值yi的相对偏差δ:
(12)
基于多元线性回归的预测值Yi与观测值yi的相对偏差γ:
(13)
为了更好地说明两种预测结果以及预测的精度,引用以下几个评价标指标[14]:
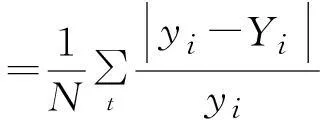
④ 相对误差平方和均值平方根:
便于分析,模糊线性回归与线性回归两种预测模型的评价指标见表4。
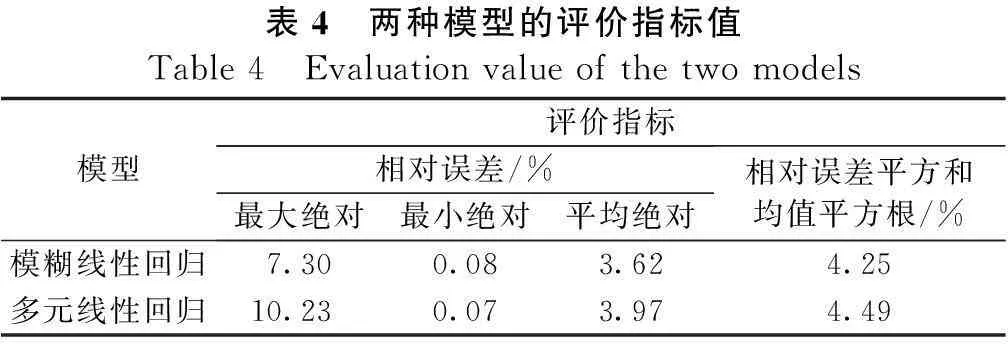
表4 两种模型的评价指标值Table4 Evaluationvalueofthetwomodels模型评价指标相对误差/%最大绝对最小绝对平均绝对相对误差平方和均值平方根/%模糊线性回归7.300.083.624.25多元线性回归10.230.073.974.49
图2、图3分别为模糊线性回归预测流量、多元线性回归预测流量与实际观测值比较。
图4为2种回归模型的交通流量的预测值与实测值的相对误差值的比较图。
从图2~图4以及表4可以得出:模糊线性回归预测流量与真实值的相对误差要偏小,最大预测相对误差绝对值为7.30%,平均绝对相对误差为3.62%,因此可以看出基于模糊线性回归的预测模型的预测精度较高,整体预测效果比较稳定,且效果要优于简单的多元线性回归方法,适合与实际工程应用。
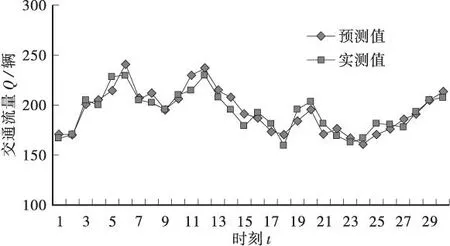
图2 模糊线性回归预测结果与实际观测值比较Figure 2 Traffic flow comparison chart between actual and predicted of fuzzy linear regression

图3 多元线性回归预测流量与实际观测值比较Figure 3 Traffic flow comparison chart between actual and predicted of multiple linear regressions

图4 2种回归模型交通预测值与实测值相对误差值比较Figure 4 Relative error value comparison chart between fuzzy linear regression prediction and multiple linear regression prediction
另外,从图4中可以看出:文中模糊线性回归预测模型的预测误差波动较小,而多元线性回归预测模型虽然拟合都较高,但拟合误差变化较大,可知,文中所建立预测模型的泛化能力[15]也优于后者。
5结论
本文针对交通流量短时变化的随机性强,抗扰能力弱等自身特点,提出了基于模糊线性回归的流量预测模型,选取柳州市城中区文昌路的实测数据进行实证分析。结果表明,文中建立的交通流量的预测模型预测结果与真实值误差较小,其拟合平均相对偏差为3.62%,总体效果良好,体现出了模型较强的泛化能力,可以适用于交通流量预测场合。最后,还将文中模糊线性回归模型的预测结果与STPS多元线性回归模型的预测结果进行了比较,可以看出,前者的预测效果要优于后者,模型精度也高于后者,因此有力验证了模糊线性回归方法在交通量预测方面的实用性,且原理上也切实可行。
[参考文献]
[1]刘丽娜.城市道路交通流量短时预测的研究[D].北京:北京邮电大学,2009.
[2]傅贵,韩国强,逯峰,等.基于支持向量机回归的短时交通流预测模型[J].华南理工大学学报(自然科学版),2013(9):105-107.
[3]刘丽娜.城市道路交通流量短时预测的研究[D].北京:北京邮电大学,2009.
[4]张康.基于模糊理论的若干城市交通问题研究[D].长沙:长沙理工大学,2008.
[6]韩超,宋苏,王成红.基于ARIMA模型的短时交通量自适应预测[J].系统仿真学报,2004,16(7):1530-1532.
[6]吴怀宇.时间序列分析与综合[M].武汉:武汉大学出版社,2004.
[7]Ben-Akiva M,Cascetta E.Recent Progress in Short-Range Traffic Prediction.Compendium of Technical Papers[J].Institute of Transportation Engineers(ITE),1993,262-265.
[8]高慧,赵建玉,贾磊.短时交通流预测方法综述[J].济南大学学报,2008,22(1):88-94.
[9]戴红.基于模糊理论的交通信息处理技术研究[D].长春:吉林大学,2007.
[10]张帆.城市交通网络流量预测方法比较[J].科技进步与对策,2004(11):57-59.
[11]汪培庄,李洪兴.模糊系统理论与模糊计算机[M].科学出版社,1996.3,第1版:166-187.
[12]耿光飞,郭喜庆.模糊线性回归法在负荷预测中的应用[J].电网技术,2002,26(4):19-21.
[13]耿光飞,郭喜庆.模糊线性回归法在负荷预测中的应用[J].电网技术,2002,26(4):19-21.
[14]胡晓健,王炜,陆建.基于自适应粒子群优化算法的交通量短时预测模[J].武汉理工大学学报:交通科学与工程版,2009,1(33):9-12.
[15]杨兆升,王媛,管青.基于支持向量机方法的短时交通流量预测方法[J].吉林大学学报:工学版,2006,36(6):881-884.
Research on the Urban Road Short-term Traffic Flow Forecast Based on Fuzzy Theory
HUANG Huiqiong
(College of Automobiles and Transportation, Guangxi University of Science and Technology, Liuzhou, Guangxi 545006, China)
[Abstract]Traffic information analysis and processing is a key point to realize the intelligent traffic management information system.Thus,the role cannot ignore in the traffic management and control.In view of the time-varying and complexity of the traffic flow,traffic volume prediction algorithm based on fuzzy linear regression model is presented based on the basis of existing research.It is very important and necessary to estimate traffic volume precisely in real-time for Urban Traffic Control System and Urban Traffic Flow Guidance System as well as for travelers and managers to make auxiliary decision from the basic traffic information.Finally,the algorithm is tested with real traffic data and compared with those given by STPS regression analysis model.The result shows that the algorithm exhibits high performance on the aspects of prediction accuracy and play a big role in real traffic volume estimation.
[Key words]traffic volume; fuzzy theory; fuzzy linear regression; volume prediction
[中图分类号]U 491.1+13
[文献标识码]A
[文章编号]1674-0610(2016)01-0172-04
[作者简介]黄慧琼(1980-),女,广西南宁人,硕士,讲师,主要从事交通运输规划与管理、交通流系统建模与仿真。
[基金项目]广西科技大学科学基金项目(1419210)
[收稿日期]2014-01-04

