基于投影变形大小的投影带和投影面选择

杨　志， 覃　辉， 文鸿雁， 袁明月

(1.广西空间信息与测绘重点实验室， 广西 桂林　541004；　2.桂林理工大学 测绘地理信息学院， 广西 桂林　541004；　3.桂林理工大学 广西矿冶与环境科学实验中心， 广西 桂林　541006)



基于投影变形大小的投影带和投影面选择

杨志1，2，3， 覃辉1，2，3， 文鸿雁1，2，3， 袁明月1，2，3

(1.广西空间信息与测绘重点实验室， 广西 桂林541004；2.桂林理工大学 测绘地理信息学院， 广西 桂林541004；3.桂林理工大学 广西矿冶与环境科学实验中心， 广西 桂林541006)

[摘要]我国国家坐标系统普遍采用高斯-克吕格正射投影( 简称“高斯投影”)，即先由地面投影到参考椭球面，再由参考椭球面投影到高斯平面。经过以上投影变换，定会引起一定的投影变形，变形的大小随投影点与大地水准面的距离不同而变化。针对该问题，工程测量中通常采用的处理方法是：a.采用任意分带形式，将中央子午线移至能控制投影变形的范围。b.根据实际需要，重新设定投影面高程。c.选定一个抵偿面。是先找到最佳中央子午线，然后计算抵偿面高程，得出最佳的投影带和投影面，通过实例计算对比，能得到最佳的投影带和投影面，在一定范围内，横坐标跨度最大，同时也能够准确的确定大地测量所需要的平面控制网的坐标系。

[关键词]高斯-克吕格正射投影； 投影变形； 中央子午线； 投影面高程； 抵偿面

1概述

对于工程测量，尤其是在城市测量，不仅有测量大比例尺地形图的任务，同时还要满足各类建筑工程和市政建筑施工放样等工作的要求。要建立经济合理的，并且要能够满足各种目的的工程平面控制网坐标系，在测绘行业是一个重要的研究方向[1]。

随着测绘技术的发展，特别是GTP定位技术，其作用不可小觑。在我国道路建设中，尤其是在实际测量铁路系统中，GTP技术的应用最为广泛。随着最近几年来高速铁路的迅猛发展，对其勘测、设计变得越来越重要，为降低或者解除高差和高斯投影导致的边长变形对工程建设施工的影响，常常需要建立适宜的独立坐标系来满足工程的要求，所以就需要向铁路独立坐标系转换[2]。但因为道路测量有其自身的特点，通常会出现测区远离中央子午线或者测区平均高程偏大，从而造成长度变形增大，很难达到工程实践精度的严格要求。为此，需要建立科学合理的与本地区相契合的独立坐标系。通常而言，铁路独立坐标系建立的办法要分两步走，首先通过使用国家坐标系已知点束缚GTP网；随后在国家坐标系椭球基本参数的基础上，运用变动中央子午线和抵偿投影面的方法来建立铁路独立坐标系[3]。

2投影变形的基本概念与精度要求

2.1投影变形概念

投影变形是指将地面观测的实际长度归算到参考椭球面后，再将椭球面上的实际长度归算到高斯投影面上的变形值。投影面和投影带的选择对于平面控制网测量中，主要是解决长度变形的问题[4]。

2.2投影变形的原因

投影变形主要由以下原因所引起[5]：

① 实际测量的边长归算到参考椭球面上的变形，其值为ΔS1，据相关公式计算，在不同高程面上对应的变形值见表1。从表1可知：ΔS1是负值，表明将地面实际测量的边长归算到参考椭球面上，总是减小的；归算边高出参考椭球面的平均高程Hm与ΔS1的绝对值成正比，ΔS1随Hm的增大而增大。

② 将参考椭球面上的边长归算到高斯投影面上的变形，其值为ΔS2，根据相关公式，可以计算每公里长度的投影变形值和相对投影变形值，见表1。

从表1可见：ΔS2的值总是正数，由此可知将椭球面上的长度投影到高斯投影面上[6]，投影变形值总是增大的；ΔS2值随着归算边两端横坐标的平均值ym的平方增大而增大，由此可知，离中央子午线距离越远，其变形值越大。

表1 不同高程面上距离的相对变形与每公里投影变形及相对投影变形值Table1 Therelativedeforamtionofdistanceindifferentheightsurface&theprojectiondistortionvaluesandrelativeprojectiondistortionvaluesperkilometer不同高程面上的相对变形每公里长度投影变形及相对投影变形值Hm/mΔS1/mmΔS1/Sy/mΔS2/mmΔS2/S010-1.61/637000101.21/81000020-3.11/318500204.91/12000030-4.71/2120003011.11/9000040-6.31/1590004019.71/15000050-7.81/1274005030.71/3200060-9.41/1060006044.31/2200070-11.01/910007060.31/1650080-12.61/790008078.71/1270090-14.11/700009099.61/10000100-15.71/63700100133.01/8000160-25.11/39000———1000-1571/6370— — —

2.3投影变形的精度要求

在各类工程建设中，施工放样工作能否顺利进行，就必须要求控制点坐标反算的边长与实地测量的边长应该相等，也就是说由上述两项归算投影改正而引起的长度变形或改正数，应该小于施工放样的精度要求[7]。即每公里变形值应小于25 mm。

3长度投影变形影响因素

3.1实际测量真实长度归化至国家统一的参考椭球面

测量的实际长度归化到国家统一的参考椭球面就会产生高差投影变形[8，9]。可按式(1)计算：

(1)

式中：D为实测水平距离；RA为长度所在方向参考椭球面法截弧的曲率半径；Hm为观测边的平均大地高。

3.2椭球面上的长度投影到高斯平面

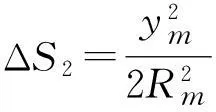
(2)

式中：S为参考椭球面的长度；Rm为测线两端平均纬度处参考椭球面的平均曲率半径；ym为测线在高斯平面上离中央子午线垂距的平均值。

3.3长度综合变形[10]

通过两次变形后，地面真实长度与高斯投影面的长度之差为长度综合变形，按式(3)计算：

(3)

在实际计算中，为了方便起见，又不影响必要的精度，取Rm=RA=6 371 km，采用不同投影面的同一距离近似相等，即S≈D，可以写成相对变形的形式为：

(4)

由公式(4)可知：采用国家统一坐标系统所产生的长度综合变形与测区内的平均高程和测区所处投影带内的位置有关，根据(4)式可以计算出已知测区内的长度相对变形的大小[11-13]。

可以把长度综合变形的容许值代入(4)式得：

H=0.783y2(10-4)±0.159

(5)

式中：以H为纵坐标轴，y为横坐标轴，式(5)绘制成图如图1所示。

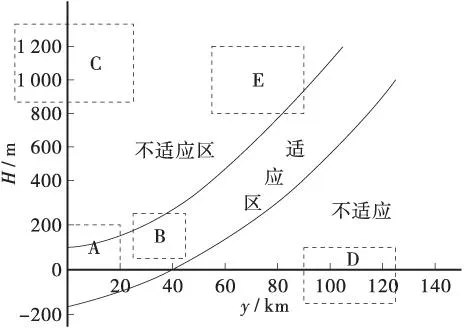
图1　投影面高程与横坐标投影变形Figure 1　The height varying in the projection surface and 　the projection varying in abscissa

图1中：适应区是指A区、B区适合采用国家统一坐标系，没有必要建立独立坐标系，其他不适应区域则需要建立独立坐标系才能满足实际需要。其中C区域为高海拔地区，长度综合变形中占主导作用的是高程归算变形；在D区域为离中央子午线较远，则投影变形占主导作用的是高斯投影所产生的变形；在E区域内则是前面两者综合影响长度变形[14]。

4实例分析

本文以一范围在东经114°22′～ 114°41′，北纬 37°52′～38°11′的区域为例进行分析比较，该地区东西距114°子午线分别为yW= 32.2 km和yE= 60.0 km。两边的平均高程为HW=80 m和HE=61 m，该地区平均高程为Hu=70 m，高程异常为Hg=40 m。由公式(6)计算横坐标区间ym，ym=(0～58.6)km。

(6)

① 当投影面高程H=0 m ，中央经线L=114°时，规划区的东西边投影变形值分别为：

西边的变形值为：

(7)

东边的边线值为：

(8)

从式(8)可知：东边投影变形值已经大于25 mm/km，所以需要选择合适的方法来解决投影变形值过大的影响。

② 当变更中央子午线L=114°30′，H=0 m时，选择投影带和投影面：

首先，计算市中心距统一3°带中央子午线114°的横坐标近似值y0：

y0=N·l·cosB=1.857·l′·cosB=43.9 km

(9)

式中：平均纬度B=38°；市中心距中央子午线114°的经差l′=30′；卯酉圈曲率半径N=6 383 km。

由式(9)可知：该区域中心位于统一3°带中央子午线(114°)以东 43.9 km，对新建的独立坐标系，则规划区东边位于中央子午线以东16.1 km(经差11′，yE=16.1 km)，规划区西边位于中央子午线(114 °30′)以西11.7 km(经差-8′，yW=11.7 km)，由此可计算出投影变形值分别为：

西边变形值：

(10)

东边变形值：

(11)

可见，中央子午线两边投影变形值都小于25 mm/km，选择过该区域中心点的子午线作为中央子午线，然后投影到H=0 m的高程面上能基本解决投影变形过大的影响。

③ 当改变投影面高程，投影到该区平均高程H=70 m的高程面上，仍选用114°为中央子午线建立独立坐标系，由式(8)可知：东边的高斯投影变形值较大，高程归化改正不能彻底的抵消其变形，假如中央子午线不改变，就只能人为的改变归化高程来抵偿部分高斯投影变形值，使其长度变形仍然小于 1/40 000。

西边的投影变形为：

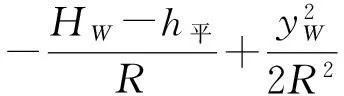
(12)

东边的投影变形为：

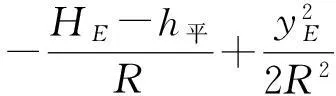
(13)

由式(13)可知：这种情况，东边的投影变形值大于25 mm/km，不能满足要求。

④ 选用114°30′为中央子午线，投影到市区平均高程H=70 m的高程面上建立标系。

西边的投影变形为：

(14)

东边的投影变形为：

(15)

可见，东西两边投影变形值都小于25 mm/km，将城区投影到H=70 m高程面上，选择过该区中心点的子午线作为中央子午线，也能够解决投影变形值过大的影响。

⑤ 计算抵偿面的高程，投影到抵偿面高程上，中央经线L=114°时。

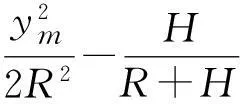
(17)

假设该区中心点y0= 43.9 km处的投影变形的变形值为0，可求出高程修正值ΔH得：ΔH=41 m，可知抵偿面的高程为：

Hd=Hu-(H+ΔH)=-81 m

(18)

这时规划区西边的归化高度为：

(19)

东面的归化高度为：

(20)

计算投影变形得：

西面的投影变形为：

(21)

东面的投影变形为：

(22)

计算抵偿带宽度，将式(19)、式(20)代入式(6)得：yW=4.59 kmyE=61.98 km

东西的横坐标跨度为：

Δy=yE-yW=57.39 km

(23)

根据式(18)、式(21)、式(22)，在不改变中央子午线(L=114°)的情况下，可以选择Hd=-81 m的抵偿高程面作为投影面，也能解决投影变形值过大的问题，但变形值还是相对较大，由式(23)也可得知，东西跨度也比较小。

⑥ 在选择Hd=-81 m低偿高程面作为投影面建立独立坐标系，同时选择过该区中心点y0= 43.9 km的子午线(经度为114°30′)作为中央子午线，此时可以计算出投影变形值为：

西边的投影变形为：

(24)

东边的投影变形为：

(25)

计算抵偿带宽度：令式(24)、式(25)的右边等于25 mm/km，计算东西边距中央子午线的最大横坐标得：

yWmax=45.124 kmyEmax=45.126 km

东西的横坐标跨度为：

Δy=yEmax+yWmax=90.25 km

(26)

从表2中可以清晰的看到：第一种方法与第三种方法变形值都超过了25 mm/km的精度要求，第二种方法东边、西边变形值都比较大，第四种方法也不是最优解，第五种改变抵偿面高程方法在实际应用中比较多，但所建立的坐标系东西变形相对较大，横坐标跨度也很小，不利于以后的城区扩建工作。而利用第六种方法，先分别计算东西归化高度，然后得到抵偿面高程，还采用最佳中央子午线建立坐标系，不但能得到投影变形值最小，并且其横坐标跨度也能够达到最大值，能充分满足城市今后规划布局的需要。

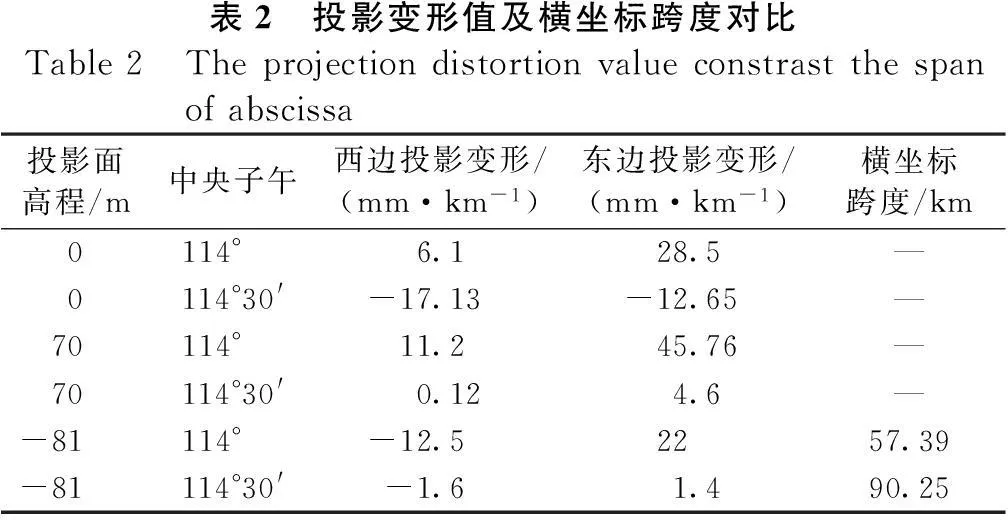
表2 投影变形值及横坐标跨度对比Table2 Theprojectiondistortionvalueconstrastthespanofabscissa投影面高程/m中央子午西边投影变形/(mm·km-1)东边投影变形/(mm·km-1)横坐标跨度/km0114° 6.128.5—0114°30'-17.13-12.65—70114° 11.245.76—70114°30'0.124.6—-81114° -12.52257.39-81114°30'-1.61.490.25

5结论

针对投影变形，通常两种手段来实现投影带和投影面的选择，首先是在已知的数据基础上，在excel表格里面进行初步计算，看投影在统一坐标系里面是否符合标准，如果不符合标准，就用两种方法解决这个问题，第一是改变投影面高程来控制变形，第二是改变投影带的中央子午线来控制投影变形。

所有测量工作的第一要务是建立准确的坐标系，这项要务是以后测量工作顺利进行的关键。上文中的六种处理的情况有几种能满足要求，但建立科学合理的城市坐标系还要依据现有的成果和城市发展规划的要求，既要考虑当前的又要着眼未来，所以为了变形最小，还有投影的有效东西跨度的最大化，在选用常用的抵偿面的基础上，采用第六种情况是最佳的选择。所以，本文的重点是讨论投影变形大小的投影带和投影面的最佳选择，是基于现实情况下的一种最佳考虑选择。

[参考文献]

[1]刘连旺，覃辉.6种曲线元上的道路中桩坐标解算[J].中南公路工程，2006.31(4)：72-76.

[2]潘国强.高速公路改扩建工程中路基加宽方式及其特点综述[J].中南公路工程，2007，32(5)：34-38.

[3]葛婷，王晓飞，符锌砂.改扩建高速公路工程交通组织方法探讨[J].中南公路工程，2010，35(6)：118-123.

[4]杨国清，王军德.假3度带坐标系及关于大城市坐标系的建议[J].测绘科学，2011，36(5)：22-24.

[5]吴云孙.浅谈广州市平面控制测量坐标系统的选取[J].测绘通报，2005(8)：42-43.

[6]覃辉.测量程序与新型全站仪的应用[M].北京：机械工业出版社，2006.

[7]范一中，王继刚，赵丽华.抵偿投影面的最佳选取问题[J].测绘通报，2000(2)：20-21.

[8]牛卓立，赖昌意.建立区域坐标系问题的讨论[J].测绘工程，1998，7(4)：13-16.

[9]许娅娅，张碧琴.公路施工测量百问[M].北京：人民交通出版社，2006.

[10]田青文.测量学(下)[M].西安：西安地质学院出版社，1994，90-115.

[11]武瑞宏.工程独立坐标系的建立方法研究[J].工程勘察，2009(3)：68-71.

[12]王继刚，王坚.具有抵偿面得任意待高斯投影直角坐标系的选取方法[J].测绘通报，2002(11)：31-32.

[13]李世安，刘经南，施闯.应用GTP建立区域独立坐标系中椭球变换的研究[J].武汉大学学报信息科学版，2005，30(10)：889-891.

[14]张华海，王宝山，赵长胜，等.应用大地测量学[M].徐州：中国矿业大学出版社，2007.

The Selection of Projection Zone and Plane is Based on the Size of Projection Distortion

YANG Zhi1，2，3， QIN Hui1，2，3， WEN Hongyan1，2，3， YUAN Mingyue1，2，3

(1.Guangxi Key Laboratory of Spatial Information and Geomatics， Guilin， Guangxi， 541004， China；2.College of Geomatics and Geoinformation， Guilin University of Technology， Guilin， Guangxi， 541004， China；3.Guangxi Scientific Experiment Center of Mining， Metallurgy and Environment， Guilin University of Technology， Guilin， Guangxi 541006， China)

[Abstract]China’s national coordinate system commonly used Gauss-Kruger orthographic projections( abbreviation “Gauss Projections” ).That is to say the projections go first to the ground，and then to the reference elliTPoid.Next，the projections will finally projected onto the Gaussian flat.After the transform of above projections，it will cause some sort of deforms.The scale of the deforms will be varied with the different distance between the projection point and the geoid.Usually.Aimed at the problem，The approaches be used in engineering survey are：a.Use the form of zonation randomly to put the central meridian to the range that the projection distortion can be able to control；b.According to the actual needs，reset the elevation of projection plane；c.Select the compensation plane.In this paper，we should find the best central meridian at first，and then calculate the elevation of compensating surface，we will get the optimal projection zone and projection plane.By analysis of calculated result obtained the optimal projection zone and projection plane and the span of abscissa is the peak of maximum within a certain range，it also be able to accurately determine the coordinate system of the plane geodetic control network at the same time.

[Key words]gauss-kruger orthographic projections； projection distortion； the central meridian； the elevation of projection plane； compensation plane

[中图分类号]U 412.24+1

[文献标识码]A

[文章编号]1674-0610(2016)01-0059-05

[作者简介]杨志(1989-)，男，湖南桃江人，研究生，变形监测与数据处理。[通讯作者] 文鸿雁(1963-)，男，湖南祁阳人，教授，博士，研究方向为精密工程测量与专题信息系统。

[基金项目]国家自然科学基金项目(41461089)；广西“八桂学者”岗位专项经费资助项目广西空间信息与测绘重点实验室资助课题(桂科能130511402，1207115-06)；广西自然科学基金基金项目(2014GXNSFAA118288)；广西矿冶与环境科学实验中心资助课题(KH2012ZD004)；广西研究生教育创新计划项目(YCSZ2014151，YCSZ2012083)

[收稿日期]2014-10-23