基于投影几何法的虎克万向节轴承的运动特性分析

陈　科　殷　磊　郭　伟　张建中，2

1.合肥工业大学，合肥，230009　　2.安徽建筑大学，合肥，230011



基于投影几何法的虎克万向节轴承的运动特性分析

陈科1殷磊1郭伟1张建中1，2

1.合肥工业大学，合肥，2300092.安徽建筑大学，合肥，230011

摘要：通过对虎克万向节运动特性的分析，利用空间坐标变换法及空间投影几何法，建立虎克万向节轴承的瞬时转角方程，并建立轴承瞬时转速分析的数值方法，分析轴承的瞬时转速及瞬时转角与轴间夹角之间的关系；采用运动仿真法验证了分析结果的正确性。分析结果表明：主动叉头的轴承瞬时转速与从动轴承的瞬时转速并不相等，主动轴承的瞬时转速的波动大于从动轴承的瞬时转速的波动。研究结果为分析虎克万向节轴承的摩擦、磨损及润滑状态提供依据。

关键词：虎克万向节；投影几何法；轴承；运动特性分析

0引言

万向节是机械传动中常用的部件，主要用来连接轴与轴(或连接轴与其他回转零件)[1]。虎克万向节具有结构紧凑，维护方便等特点，是一种应用最广泛的挠性万向节。虎克万向节由两个叉头及一个十字轴组成，十字轴和叉头存在相对旋转运动[2]。为了减少十字轴轴颈和叉头之间的摩擦，通常采用轴承将两者连接，十字轴轴颈和叉头之间的相对转速即为轴承的转速。文献[2-3]指出虎克万向节在工作时，其轴承并非做完整的旋转运动，而是做往复摆动，旋转方向在轴承未旋转一圈时就已改变。文献[4]指出摆动轴承的疲劳寿命与轴承的摆幅角有关。文献[5]指出轴承中的各部件的运动状态由轴承的转速决定。文献[6]进一步指出轴承内各元件的运动状态又与其润滑状态密切相关。此外，轴承中滚子的速度引起的动态载荷将显著影响球轴承的接触角、径向游隙及滚动体载荷分析；轴承中的摩擦力矩及摩擦发热也受到轴承转速的影响[4]。由上述分析可知，虎克万向节轴承的运动状态对其疲劳寿命、动载荷、摩擦磨损及传动效率有重要影响。因此有必要计算虎克万向节轴承的运动特性，为虎克万向节中轴承的设计、制造提供依据。

虎克万向节中的轴承用于连接十字轴与叉头，因此其运动特性由十字轴和叉头的运动特性决定。文献[7-8]指出十字轴的运动为绕定点的转动，并引入欧拉旋转矩阵、接触广义坐标与欧拉角之间的换算关系，将传统的欧拉运动方程、欧拉动力学方程配以矩阵形式，解出十字轴的三维瞬轴方程、绕瞬轴角速度、角加速度及惯性力矩。文献[9-10]采用坐标变换法分析了叉头的运动特性，并指出从动叉头与主动叉头之间可能存在运动干涉。文献[11]将十字轴的瞬时角速度矢量简化为二维平面矢量，推导出了虎克万向节轴承的运动方程，但是由于十字轴的转速并非二维矢量，而是三维矢量，因此文献[11]的分析结果与轴承的真实运动状态存在相当大的差距。

1建模与求解

1.1瞬时转角分析

在虎克万向节中，轴承的内圈随十字轴轴颈回转，外圈随叉头的轴承孔回转。当滚动体是圆柱滚子或滚针时，为了提高虎克万向节的叉头及十字轴的强度，轴承没有内圈及保持架，这时十字轴的轴颈起到内圈的作用。因此轴承的转速即为十字轴相对于叉头孔轴线的瞬时转速。通常可以采用方向余弦矩阵法、投影几何法或四元数法等求解该瞬时速度，本文采用投影几何法对其进行分析。

图1　万向十字轴布置示意图

分析时万向节的初始位置如图1所示，叉头1所在平面平行于纸面，为主动叉头；叉头2所在平面垂直于纸面，为从动叉头；叉头1的轴线与叉头2的轴线夹角为β。轴承A、轴承A′安装于叉头1，A、A′为轴承A、轴承A′的几何中心；轴承B、轴承B′安装于叉头2，B、B′为轴承B、轴承B′的几何中心；O为十字轴轴颈的轴线AA′、BB′的交点，即十字轴的中心。为分析轴承的运动规律，建立图2所示的坐标系。其中，坐标系的原点位于点O，X轴与叉头1的轴线平行，Y轴与轴线AA′平行，Z轴与轴线BB′平行，方向如图2a所示。十字轴的长度为r，则在初始位置时，A点的坐标为(0,-r,0)，B点的坐标为(0,0,r)。如图2b所示，轴承A、轴承A′的转角等于十字轴绕轴AA′的转角，该转角可由B点绕轴线AA′的转角表示；投影平面P为垂直于轴线AA′的平面，OP、BP分别为点O、点B在投影平面P的投影，因此B点绕轴线AA′的转角等于BP在投影平面P上绕OP的转角。由文献[2]可知，轴承A(A′)的摆角为β，如图3所示。由文献[12]可知，B(B′)点的连线在纸面上的投影为直线a，如图3所示。由图4可知，在初始位置时，轴承A(A′)的转角为0，即在平面P上，BP绕OP的转角为0。

(a)万向节运动示意图

(b)十字轴运动投影图图2　轴承运动分析示意图

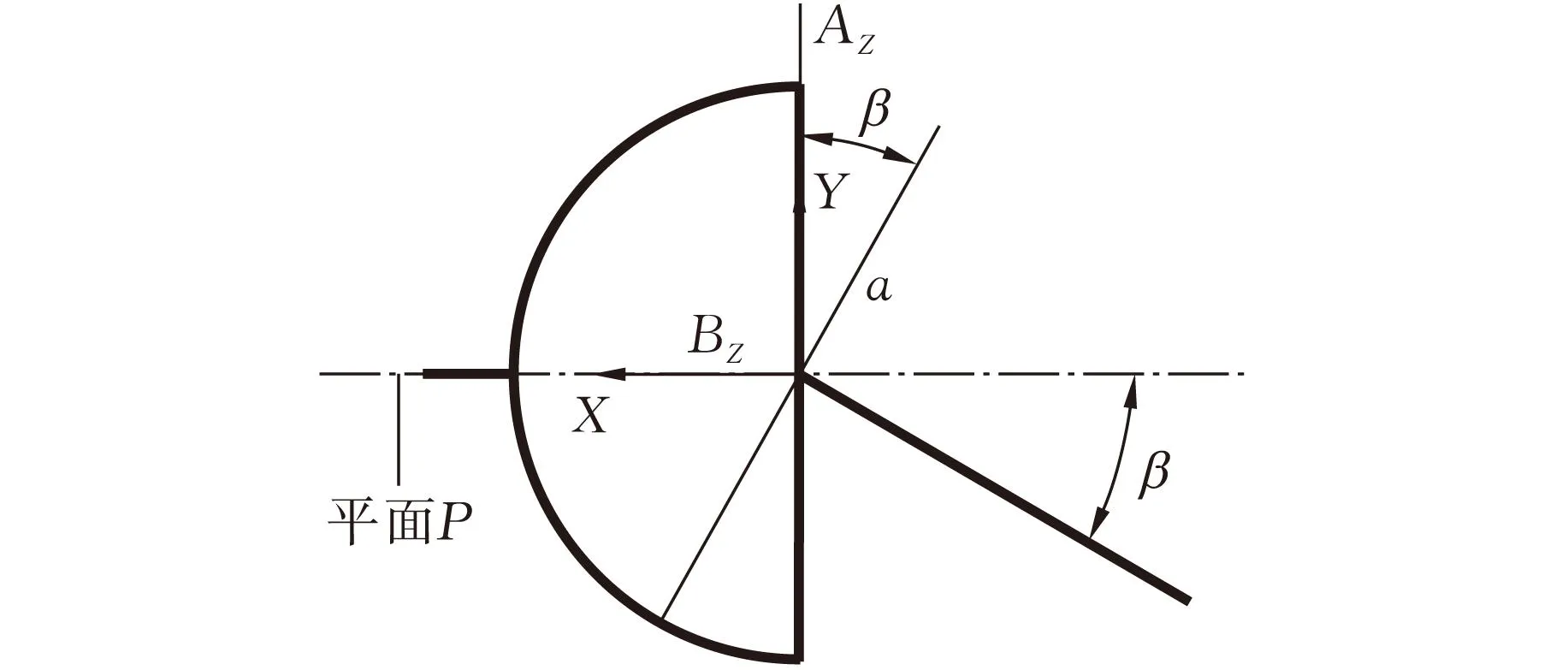
图3　初始位置时万向节在纸面的投影

图4　初始位置时万向节在平面P的投影

设叉头1的转角为φ1，A点的坐标为(0,-cosφ1,-sinφ1)，B点的坐标为(x,y,z)。由文献[13]可知，B点的运动轨迹在以O点为球心的球面上，因此

x2+y2+z2=r2

(1)

由十字轴的结构可知，OA⊥OB,因此

cosφ1y+sinφ1z=0

(2)

由万向节的结构可知，十字轴的轴颈OB垂直于叉头2的轴线Ⅱ,因此

xsinβ+ycosβ=0

(3)

由式(1)~式(3)可知，B点的坐标y为

(4)

式(4)中，0°<φ1≤180°时，取正号；180°<φ1≤360°时，取负号。叉头1的转角为φ1时，万向节在纸面的投影如图5所示；在平面P的投影如图6所示，θ为B点绕AA′轴的转角，即轴承A的转角。由于平面P垂直于AA′轴，因此平面P绕叉头1的轴线Ⅰ的转角为φ1，此时纸面与平面P的夹角为90°-φ1。B点在平面P的投影BP与其在纸面的投影BZ之间的关系可由图7求出，其中

(5)

(6)

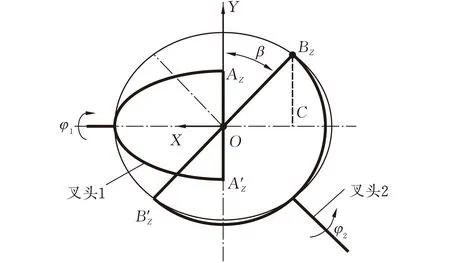
图5　叉头1转角为φ1时万向节在纸面的投影

图6　叉头1转角为φ1时万向节在平面P的投影

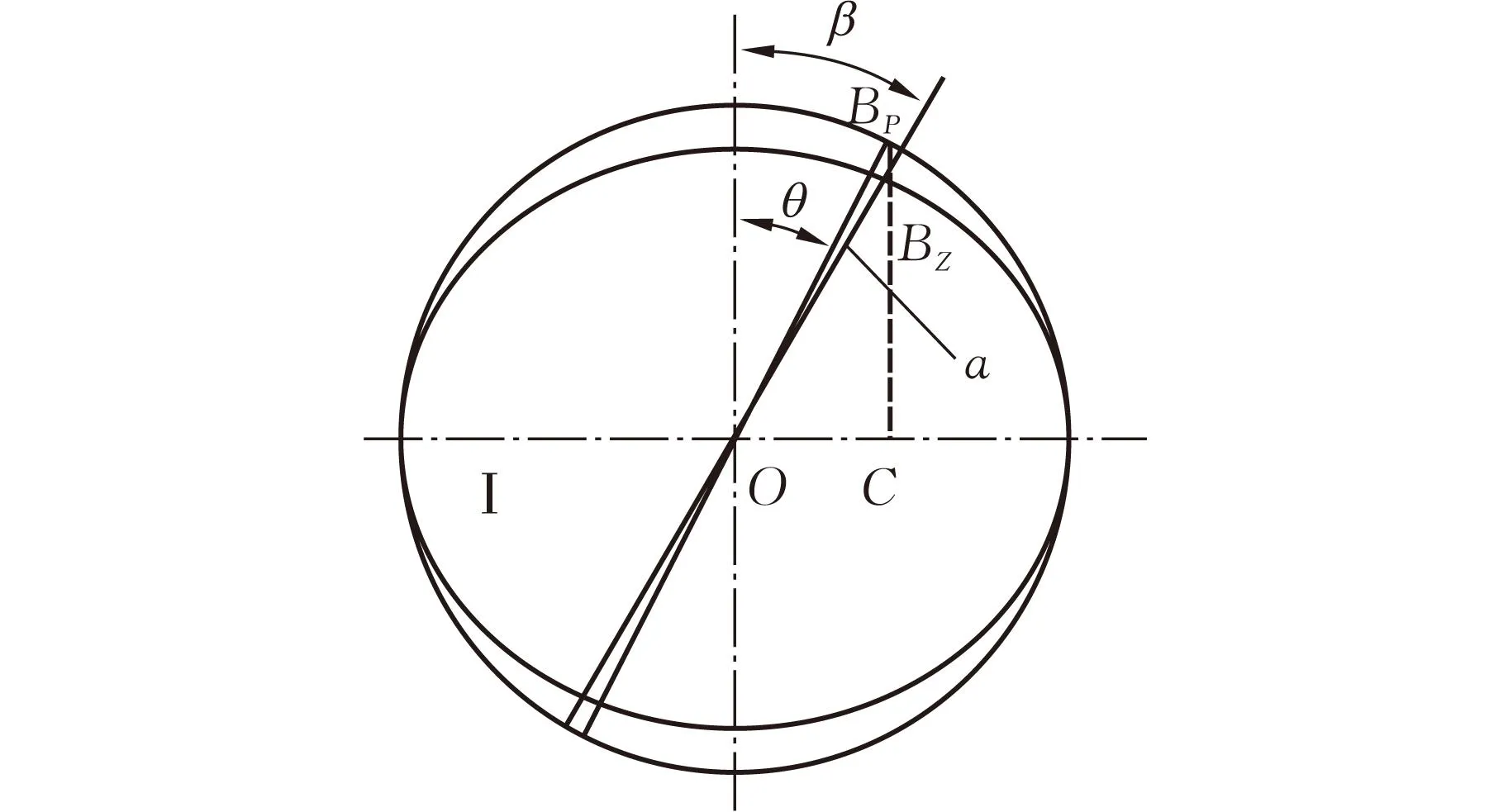
图7　BP与BZ投影关系示意图

由B点的坐标y即可求出lBZC:

(7)

即

(8)

由图2可知，lOBP的长度为r。因此，由式(5)、式(6)及式(8)可知

(9)

即

(10)

式(10)即为轴承A(A′)的转角公式。其中，0°<φ1≤180°时，取正号；180°<φ1≤360°时，取负号。

由图8可知，当叉头1的转角为90°时，轴AA′垂直于纸面，此时平面P与纸面平行。由于轴间夹角(轴Ⅰ与轴Ⅱ的夹角)为β，并且APOP垂直于轴Ⅰ、BPOP垂直于轴Ⅱ，因此BP绕OP的转角为β，即轴承A(A′)的转角为β，该结果与文献[3]中的结论一致，从而证明了上文中采用的投影几何方法的正确性。当叉头1的转角为90°时，将φ1=90°代入式(10)可得θ=β,因此可以证明式(10)的正确性。

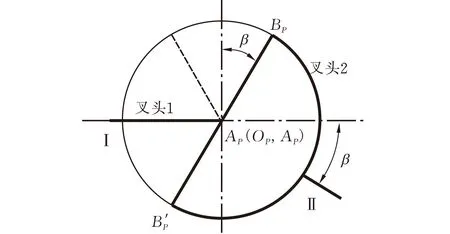
图8　叉头1转角为90°时万向节在纸面(平面P)的投影

若将叉头2的转角φ2代替式(10)中叉头1的转角φ1，即可获得轴承B(B′)的瞬时转角θ′的计算公式：

(11)

由文献[2]可知，叉头1的转角φ1与叉头2的转角φ2之间的关系为

tanφ2=tanφ1cosβ

(12)

将式(12)代入式(11)可得

(13)

式(13)即为轴承B(B′)的瞬时转角θ′的表达式。由上述分析可知，虽然轴承A(A′)与轴承B(B′)的摆动半角的都为β，但是两者的瞬时转角并不相等。

1.2瞬时转速分析

对式(11)、式(13)进行求导，可获得轴承A(A′)、轴承B(B′)的瞬时转速公式。式(11)、式(13)导函数的解析解虽然能求出，但是形式复杂，因此本文采用数值微分的方法求解式(11)、式(13)的导数。数值微分方法根据式(11)、式(13)在一些离散点的函数值，计算其在某点的导数(即角速度)。本文采用较高精度(精度为O(h2))的三点数值微分法，其公式为

(14)

其中x0，x1,…，xn为微分节点，ξ∈[x0，x1，…，xn]。

2运动学实例分析和验证

2.1瞬时转角分析

根据上节所述方法和公式，在MATLAB中编写相应程序，可以得出不同轴间夹角对轴承瞬时转角的影响；计算时保持叉头1的转速为30 r/min。如图9所示，万向节中轴承的运动周期等于万向节的转动周期，轴承的摆动半角等于轴间夹角β，轴承的摆动半角随轴间夹角β增大而增大，当轴间夹角β为0时，轴承的摆动半角为0，即轴承在万向节的传动过程中保持静止。此外，轴承A(主动叉头的轴承)的瞬时转角与轴承B(从动叉头的轴承)的瞬时转角并不相同，且轴间夹角β越大，两者的瞬时转角差越大。

图9　轴承瞬时转角分析

2.2瞬时转速分析

根据1.2节所述的方法，在MATLAB中编写相应程序，可以得出不同的轴间夹角对轴承的转速的影响，计算时保持叉头1的转速为30 r/min。如图10所示，轴承A(A′)与轴承B(B′)的速度变化周期等于万向节的运动周期。轴承运转的速度波动受轴间夹角β的影响：轴间夹角β越大，轴承转速波动的振幅越大；当轴间夹角β为0时，轴承的转速恒为0。轴承A(A′)的瞬时转速不等于轴承B(B′)的瞬时转速，轴承A(A′)的转速波动的振幅大于轴承B(B′)的转速波动的振幅。

图10　轴承瞬时转速分析

3结果验证

为了验证上文中的分析结果的正确性，本节建立十字轴式万向节的三维模型，并采用多体动力学软件Solidworks Motion对其进行运动分析。运动仿真模型如图11所示，其中机座为固定不动的部件，旋转马达设置在叉头1的圆柱面上，转速为30 r/min。在十字轴式万向节的运动仿真模型中，所有相互连接的刚体之间皆施加铰链配合，即连接的一对刚性物体之间只存在一个绕其公共圆柱接触面轴线的相对转动自由度，其他自由度皆被约束。仿真分析结果与上节计算结果的对比如图12所示：仿真分析所获得的轴承A的瞬时转角、瞬时转速与上节计算所得瞬时转角、瞬时转速精确吻合,从而证明上节所获轴承的瞬时转角及转速公式是准确可靠的。

图11　运动仿真模型

(a)轴承A的瞬时转角θ计算值与仿真值的对比

(b)轴承A的瞬时转速ω计算值与仿真值的对比图12　运动仿真结果与理论计算结果的互证

4结论

(1)虎克万向节轴承的运动为摆动运动，而非整圈的转动，运动的周期与万向节的转动周期相同，摆动的半角与虎克万向节的轴间夹角相同。

(2)主动叉头的瞬时转角与从动叉头的瞬时转角并不相同,主动叉头的瞬时转角大于从动叉头的瞬时转角；且轴间夹角越大，两者的瞬时转角差越大。

(3)轴承的瞬时转速的波动随着轴间夹角的增大而增大，转速的波动周期与万向节的转动周期相同，主动叉头的瞬时转速与从动叉头的瞬时转速不相等，主动叉头的瞬时转速大于从动叉头的瞬时转速,且轴间夹角越大，两者的瞬时转速差越大。

上述结论为分析虎克万向节叉头轴承中的各部件的运动状态提供了依据，进而为分析轴承的摩擦磨损、润滑状态及疲劳寿命等提供了依据。

参考文献：

[1]濮良贵，纪名刚．机械设计[M]．7版．北京：高等教育出版社，2001．

[2]Schmelz F，Seherr-Thoss H C，Aucktor E．Universal Joints and Driveshafts：Analysis， Design，Application[M]．2ed．Berlin: Springer-Verlag，2006.

[3]羊拯民．传动轴和万向节[M]．北京：人民交通出版社，1995．

[4]Harris T A,Kotzalas M N.滚动轴承分析(第1卷)[M]．罗继伟，马伟，杨咸启，等译．5版．北京：机械工业出版社，2009．

[5]Harris T A,Kotzalas M N.滚动轴承分析(第5卷)[M]．罗继伟，马伟，杨咸启，等译．5版．北京：机械工业出版社，2009．

[6]温诗铸，黄平．摩擦学原理[M]．3版．北京：清华大学出版社，2008．

[7]朱金榴．万向联轴器十字轴的运动学和动力学方程[J]．上海工程技术大学学报，1996(3)：26-30．

Zhu Jinliu．Kinematics and Kinetics Equations of Universal Pins at Universal Couplings[J]．Journal of Shanghai University of Engineering Science, 1996(3): 26-30.

[8]朱金榴，马卫华，胡秉辰．双万向联轴器动力学分析[J]．吉林工业大学学报，1996, 26(82)：77-81．

Zhu Jinliu, Ma Weihua, Hu Bingchen. Dynamic Analysis of Double Universal Couplings[J]. Journal of Jilin University of Technology, 1996, 26(82):77-81.

[9]Hummel S R，Chassapis C． Configuration Design and Optimization of Universal Joints[J]．Mechanism and Machine Theory，1998，33(5)：479-490．

[10]Hummel S R，Chassapis C．Configuration Design and Optimization of Universal Joints with Manufacturing Tolerances [J]．Mechanism and Machine Theory，2000,35(3)：463-476．

[11]谭国宏，孙孝元．十字轴的运动、受力分析及其修形量的计算[J]．重型机械，1993(2):32-35．

Tan Guohong, Sun Xiaoyuan. Force, Kinematic Analysis of Universal Pins and Calculation of Its Shape Modification[J]. Heavy Machinery, 1993(2): 32-35.

[12]陈科，殷磊，高峰，等．双联虎克万向节凸缘叉相位角对传动特性影响的分析[J]．中国机械工程，2013，24(17)：2323-2327．

Chen Ke, Yin Lei, Gao Feng, et al. Influence of Phase Angle between Flange Yokes on Transmission Characteristics of a Double Hooke’s Universal Joint[J]. China Mechanical Engineering, 2013, 24(17): 2323-2327.

[13]Guo Y, Sun Z and Sun Z．The Kinematics Analysis on Single Cross Universal Joint[C]// Vehicle Power and Propulsion Conference. Harbin：IEEE，2008：1-3．

(编辑王旻玥)

Motion Characteristic Analysis of Bearings in Hooke’s Joint Based on Perspective Geometry

Chen Ke1Yin Lei1Guo Wei1Zhang Jianzhong1,2

1.Hefei University of Technology,Hefei,2300092.Anhui Jianzhu University,Hefei,230011

Abstract：The formulas of bearing rotation angle in Hooke’s joint were established based on the coordinate transformation method and space perspective geometry according to the analysis of kinetics’ behaviors of the Hooke’s joint. A numerical method for calculating bearing rotation speed in Hooke’s joint was set up. By adaption of above mentioned formulas and numerical method, the relations among instantaneous rotation angle, rotational speed and true joint angle were analyzed, and the results were validated by kinematics simulation. The results indicate that the bearing rotation speed in driving fork is higher than that in driven fork and the bearing rotation speed wave in driving fork is higher than that in driven fork. The conclusions obtained give basis for analysis of friction, abrasion and lubrication state of bearings in Hooke’s joint.

Key words：Hooke’s joint;space perspective geometry;bearing;motion characteristic analysis

作者简介：陈科，男，1965年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为机电产品的现代设计理论与方法，人工神经网络和进化算法等在机械产品中的应用，机电产品的CAD/CAE/CAM。殷磊，男，1985年生。合肥工业大学机械与汽车工程学院博士研究生。郭伟，男，1991年生。合肥工业大学机械与汽车工程学院硕士研究生。张建中，男，1972年生。安徽建筑大学电子与信息工程学院副教授，合肥工业大学机械与汽车工程学院博士研究生。

中图分类号：TH133.4

DOI：10.3969/j.issn.1004-132X.2016.06.005

基金项目：安徽省高等学校省级自然科学研究项目(KJ2013B064)

收稿日期：2015-03-30