基于双目标双矩阵对策的水面舰艇火力分配研究*
施君杰 宋业新
(海军工程大学理学院 武汉 430033)
基于双目标双矩阵对策的水面舰艇火力分配研究*
施君杰宋业新
(海军工程大学理学院武汉430033)
摘要在海上水面舰艇多冲突复杂环境下,为了提高作战效能,针对作战双方的毁伤效能和打击时间两个目标进行研究,根据给定的毁伤效能和打击时间双目标的定义得到双方对抗下的目标支付函数,通过建立水面舰艇火力分配的双目标双矩阵对策模型,运用熵权法对对策模型中的双目标进行分析处理,将双目标双矩阵对策模型转化为单目标双矩阵对策,寻求纳什均衡解进而得出双目标条件下的最优火力分配策略,最后论文进行了仿真计算,所得结果说明了该模型具有一定的实用性和推广价值。
关键词水面舰艇; 火力分配; 双目标双矩阵对策; 纳什均衡
Warship Formation Firepower-assignment Based on Double Objective Dual Matrix Game
SHI JunjieSONG Yexin
(College of Science, Naval University of Engineering, Wuhan430033)
AbstractIn the warship formation multi-conflict complex situation on the sea, in order to improve the operational effectiveness, the damage effectiveness and strike time of two targets are researched. According to the definition of the given damage efficiency and strike time, the target payment function is obtained. Through building the double objective matrix game model of surface vessel firepower-assignment, using the Entropy weight method, the aggregation model can be solved by transforming it into a single objective double matrix game. The Nash equilibrium solution is seeken to get the best firepower-assignment strategy of double objective. At last the simulation result shows that the sequential game has practicability and popularization value.
Key Wordssurface vessel, firepower-assignment, double objective dual matrix game, Nash equilibrium
Class NumberO225
1引言
现代化海战中环境复杂多变,水面舰艇作为海上主要作战武器,随着信息化、智能化海战的突飞猛进,影响整体作战效能的各种目标因素越来越显著,而火力分配又是海上水面舰艇作战的重要内容[1~3],因此考虑多目标条件下的火力分配尤为重要,火力打击策略[4]选择的合理与否也将直接影响作战效果与战斗力的发挥。
火力分配是海上水面舰艇作战指挥的核心问题,也是亟待解决的重大理论和应用研究问题。文献[5]通过改进和优化算法来讨论复杂情况下的火力分配问题,但没能给出具体的火力分配对策模型;文献[6]基于毁伤效能目标函数的基础上研究了火力分配,文献[7~8]给出了火力分配的具体对策集结模型,但这些研究都只考虑了单目标情况下的对策集结模型,不能较全面地分析信息化海战中多目标的火力分配问题。
本文通过描述海上水面舰艇火力分配问题,建立了毁伤效能[9]和火力打击时间[10]两个目标函数的双矩阵对策模型,运用熵权法[11]对集结模型进行加权和,不仅给出了具体的对策集结模型[12],而且还得到了在双目标条件下的最优火力分配策略。
2基于双目标双矩阵对策的火力分配
2.1基于毁伤效能和打击时间双目标的火力分配问题描述
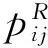
其中变量i=1,2,…,M;j=1,2,…,N。
在实际作战情况中,水面舰艇的作战单元在每阶段攻防对抗过程中使用的武器是有限的,即每阶段的作战单元数是有限的,并且在攻防对抗的全过程中,使用的武器总数亦为有限的。
在红蓝舰艇双方采取不同攻防策略形成的各个局势下,定义打击时间为火力打击单元从接受命令至摧毁对方火力单元过程中所耗费的时间,该打击时间在作战效能评估中是不可忽略的因素,因此缩短攻防双方打击时间是提高作战效能的重要措施。
假设红、蓝舰艇双方火力单元都采取直接攻击的方式,即舰艇双方同时进入海上作战区域,各舰艇火力打击单元在接受打击命令后,不必进行显著机动,直接装订目标参数对对方火力目标进行打击。直接攻击的火力打击时间由发射准备时间和武器全弹道飞行时间两部分组成。在实际作战情况下,打击节点的发射准备过程仅有参数装订一个动作,该过程耗时极短,可忽略不计。因此,本文研究的火力打击时间是由射程、武器飞行速度和双方打击策略所决定。
2.2基于毁伤效能和打击时间双目标函数的火力分配对策模型建立


根据攻防对抗的特点,每个阶段都是一个博弈过程,可将红蓝舰艇分别作为一个局中人考虑。依据各阶段的攻防对抗双方的策略,假设红蓝舰艇双方分别采取策略αu和βv,可得第一阶段红蓝舰艇双方第i个火力单元和第j个火力单元的存活概率分别为
(1)
(2)
式中Ri(0),Bj(0)分别表示红蓝双方各火力单元的初始存活概率,分析可知Ri(0)=1,Bj(0)=1。
由式(1)、式(2),同时考虑己方所有火力单元的存活概率与敌方存活概率的损失,定义对应的第一阶段红蓝双方毁伤效能支付函数分别为
(3)
(4)
根据火力打击时间的定义和双方所采取的策略集,定义红蓝双方打击时间的支付函数分别为
(5)
(6)
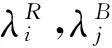
(7)
R*为各火力单元的最小存活概率,当Ri,j≥R*时,延误系数与存活概率成反比,若某个火力单元未受到对方火力打击,则延误系数为1;当Ri,j 基于红蓝双方毁伤效能和打击时间双目标的支付函数,可得攻防对抗的支付矩阵分别为R1,B1;R2,B2。 则红蓝舰艇双方基于毁伤效能和打击时间为双目标函数的火力分配可构建出双矩阵对策模型为:G={SR,SB,R1,B1,R2,B2}。 3双目标双矩阵对策模型的求解 首先采用极差变换法将双矩阵对策模型中各单目标下的支付矩阵变换成标准矩阵,针对第l(l=1,2,…,L)个目标下的支付矩阵Rl和Bl,取 对于正向目标l,令 对于逆向目标l,令 (8) 因此,将Rl和Bl标准化后的支付矩阵分别为El和Fl,则 基于El和Fl,运用熵权法确定各目标函数的权重,计算第l个目标的熵值: (9) 式中: 计算第l个目标的差异指数为 gl=1-hl (10) 对于单个目标而言,其差异指数值越大,可知该目标的作用越大。因此,可得第l个目标的权重: (11) 将红蓝舰艇双方的双矩阵对策模型中各个目标函数的支付矩阵El和Fl进行加权和,即令 (12) 式中: 通过加权和,将双目标双矩阵对策模型转化为单目标双矩阵对策模型G*={SR,SB,E,F},根据双矩阵对策与数学规划的关系,将G*的纳什均衡解转化为二次规划问题,利用lingo软件求解二次规划的最优解即为红蓝舰艇双方最优火力分配策略。 4仿真算例 4.1案例假定 设置仿真参数如下,假定红蓝舰艇双方在某海域进行攻防对抗,舰艇双方各有两个不同的火力武器单元,进行一个阶段的攻防对抗,即M=N=2,K=1,i=1,2,j=1,2,R*=0.2,攻防双方的毁伤概率为 双方舰艇之间的距离为50km,各武器单元飞行的速度分别为 4.2结果与分析 依据上述算法,建立红蓝舰艇攻防对抗的双矩阵对策模型为:G={SR,SB,R1,B1,R2,B2}。 红方舰艇火力分配的纯策略集为:SR={α1,α2,…,α4}。其中: 下面以α1为例,说明攻击策略的具体含义。α1表示红方舰艇采取的一种攻击策略,即:在攻防对抗中,红方舰艇的1号和2号武器单元同时攻击蓝方舰艇的1号作战单元。 同理可知,蓝方舰艇火力分配的纯策略集为:SB={β1,β2,…,β4}。其中: 根据以上已知条件,针对毁伤效能目标函数,利用式(3)、式(4)计算可得红蓝舰艇双方的支付矩阵分别为 针对打击时间目标函数,利用式(5)~式(7)计算可得红蓝舰艇双方的支付矩阵分别为 根据式(8)将上述不同目标函数下的支付矩阵分别变换成标准化矩阵如下: 由式(9)~式(11)两个目标的熵值分别为h1=0.9695,h2=0.9716;差异指数分别为g1=0.0305,g2=0.0284;可得各目标的权重分别为ω1=0.5180,ω2=0.4820。最后由式(12)得出: 利用lingo软件可以求得毁伤效能和打击时间两个单目标双矩阵的纳什均衡解分别为 r1=(0,1,0,0),b1=(0,1,0,0) r2=(0,0,0,1),b2=(1,0,0,0) 表示在只考虑毁伤效能目标时,最优策略为红方舰艇选择策略α2,蓝方舰艇选择策略β2;在只考虑火力打击时间目标时,最优策略为红方选择策略α4,蓝方选择策略β1。 同时可得出双目标双矩阵对策综合集结模型的纳什均衡解为e=(0,0,0,1),f=(0,0.4221,0,0.5779),表示红蓝作战双方在同时考虑毁伤效能和打击时间双目标时,红方选择策略α4,蓝方以0.4221的概率选择β2,以0.5779的概率选择β4为双方的最优混合策略。 分析以上所得结果可知,在双目标条件下所得的毁伤效能和打击时间都没有在单目标条件下更优,但如果只考虑单目标条件下的火力分配最优策略是不够全面的,在实际作战中往往会顾此失彼,顾及了毁伤效能的最优化,但是打击时间很长,导致弹药消耗量增多,作战时间延长会影响整体作战效能;如果只顾及缩短火力打击时间,但是打击效果并不是很理想,都会影响作战的整体效果。所以,只有在同时考虑两个或者多个目标时,所采取的最优策略才能更加贴近实战环境,有助于提高整体作战效果。 5结语 本文以假定的红蓝两个水面舰艇作战为背景,通过对毁伤效能和打击时间两个目标进行研究,针对红蓝双方对抗中的两个目标的支付函数,建立了火力分配的双目标双矩阵对策集结模型,运用熵权法对对策模型中的双目标进行加权和,将双目标双矩阵对策模型转化为单目标双矩阵对策进行求解,寻求纳什均衡解进而得出双目标条件下的最优火力分配策略。本文最后通过仿真案例进行了求解与讨论并得到了较好的验证结果,可见基于双目标双矩阵对策下对火力分配问题进行研究对军事领域具有重要的实际意义。但是,对于真实复杂的战场环境下,影响作战效能的目标因素有很多,而且作战常分为多个阶段的对抗,因此,多阶段多目标条件下的水面舰艇火力分配问题还有待于进一步分析研究。 参 考 文 献 [1] 李勇君,黄卓,郭波.武器-目标分配问题综述[J].兵工自动化,2009,28(11):1-5. LI Yongjun, HUANG Zhuo, GUO Bo. Review of Weapon-Target Assignment Problem[J]. Ordnance Industry Automation,2009,28(11):1-5. [2] Y. Li, X. Liu, L. Pan. The fire distribution method of multi-type missiles based on dynamic programming[C]//Proceedings of ICCET 2010-2010 International Conference on Computer Engineering and Technology,2010:1198-1200. [3] 刘传波,邱志明,吴玲,等.动态武器目标分配问题的研究现状与展望[J].电光与控制,2010,17(11):43-47. LIU Chuanbo, QIU Zhiming, WU Ling, et al. Review on Current Status and Prospect of Researches on Dynamic Weapon Target Assignment[J]. Electronics Optics & Control,2010,17(11):43-47. [4] 朱延广,朱一凡.基于影响网络的联合火力打击目标选择方法研究[J].军事运筹与系统工程,2010,24(3):64-69. ZHU Guangyan, ZHU Yifan. Research on the Selection Method of Combined Fire Strike Target Based on Influence Network[J]. Military Operations Research and Systems Engineering,2010,24(3):64-69. [5] 王少蕾,陈维义,顾雪峰.改进差分进化算法求解舰艇编队防空火力分配[J].现代防御技术,2013,41(5):58-63. WANG Shaolei, CHEN Weiyi, GU Xuefeng. Solving Weapon-Target Assignment Problems in Naval Warship Formation’s Air Defense Based on Improved Differential Evolution Algorithm[J]. Modern Defence Technology,2013,41(5):58-63. [6] 黄寒砚,王正明.武器毁伤效能评估综述及系统目标毁伤效能评估框架研究[J].宇航学报,2009,30(3):827-836. HUANG Hanyan, WANG Zhengming. Evaluation of Weapon Damage Effectiveness and Framework of System Target Damage Effectiveness Evaluation[J]. Journal of Astronautics,2009,30(3):827-836. [7] 马飞,曹泽阳,刘晖.基于博弈论的目标分配策略空间构建与搜索[J].系统工程与电子技术,2010,32(9):1941-1945. MA Fei, CAO Zeyang, LIU Hui. Construction and search of strategy space of target assignment based on game theory[J]. Systems Engineering and Electronics,2010,32(9):1941-1945. [8] 孙涛,蔡畅,王磊.舰艇编队防空火力分配多准则微分对策模型研究[J].舰船电子工程,2010,30(5):42-46. SUN Tao, CAI Chang, WANG Lei. Research on Multi-criterions DG Model for Solving Vessel Formations Firepower-assignment in Air Defense[J]. Ship Electronic Engineering,2010,30(5):42-46. [9] 曾松林,王文恽,张毅.基于动态博弈的目标分配方法研究[J].电光与控制,2011,18(2):26-30. ZENG Songlin, WANG Wenyun, ZHANG Yi. Target Allocation Method Based on Dynamic Game[J]. Electronics Optics & Control,2011,18(2):26-30. [10] 赵炤,周经伦,罗鹏程.打击时敏目标作战火力打击时间建模方法及其应用[J].海军工程大学学报,2010,22(6):42-46. ZHAO Zhao, ZHOU Jinglun, LUO Pengfei. Modeling method on striking-time of operation for time-sensitive-target-striking[J]. Journal of Naval University of Engineering,2010,22(6):42-46. [11] 宋业新,瞿勇,吴艳杰.多冲突环境下的多目标双矩阵对策集结模型[J].华中科技大学学报,2009,37(6):32-35. SONG Yexin, QU Yong, WU Yanjie. Integration model of multi-objective bimatrix games in multi-conflict situations[J]. J. Huazhong Univ. of Sci. & Tech,2009,37(6):32-35. [12] 吴艳杰,宋业新,曾宪海.两人多冲突环境下的双矩阵对策集结模型[J].海军工程大学学报,2009,21(1):22-25. WU Yanjie, SONG Yexin, ZENG Xianhai. Integration model of bimatrix games in two-person multi-conflict situations[J]. J. Huazhong Univ. of Sci. & Tech,2009,21(1):22-25. 中图分类号O225 DOI:10.3969/j.issn.1672-9722.2016.03.015 作者简介:施君杰,男,硕士研究生,研究方向:军事系统建模与运筹决策。宋业新,男,教授,博士生导师,研究方向:军事系统建模、优化决策、对策理论。 收稿日期:2015年9月4日,修回日期:2015年10月21日