降雨条件下非饱和朗肯土压力统一解
赵均海 殷佳 张常光 杜文超


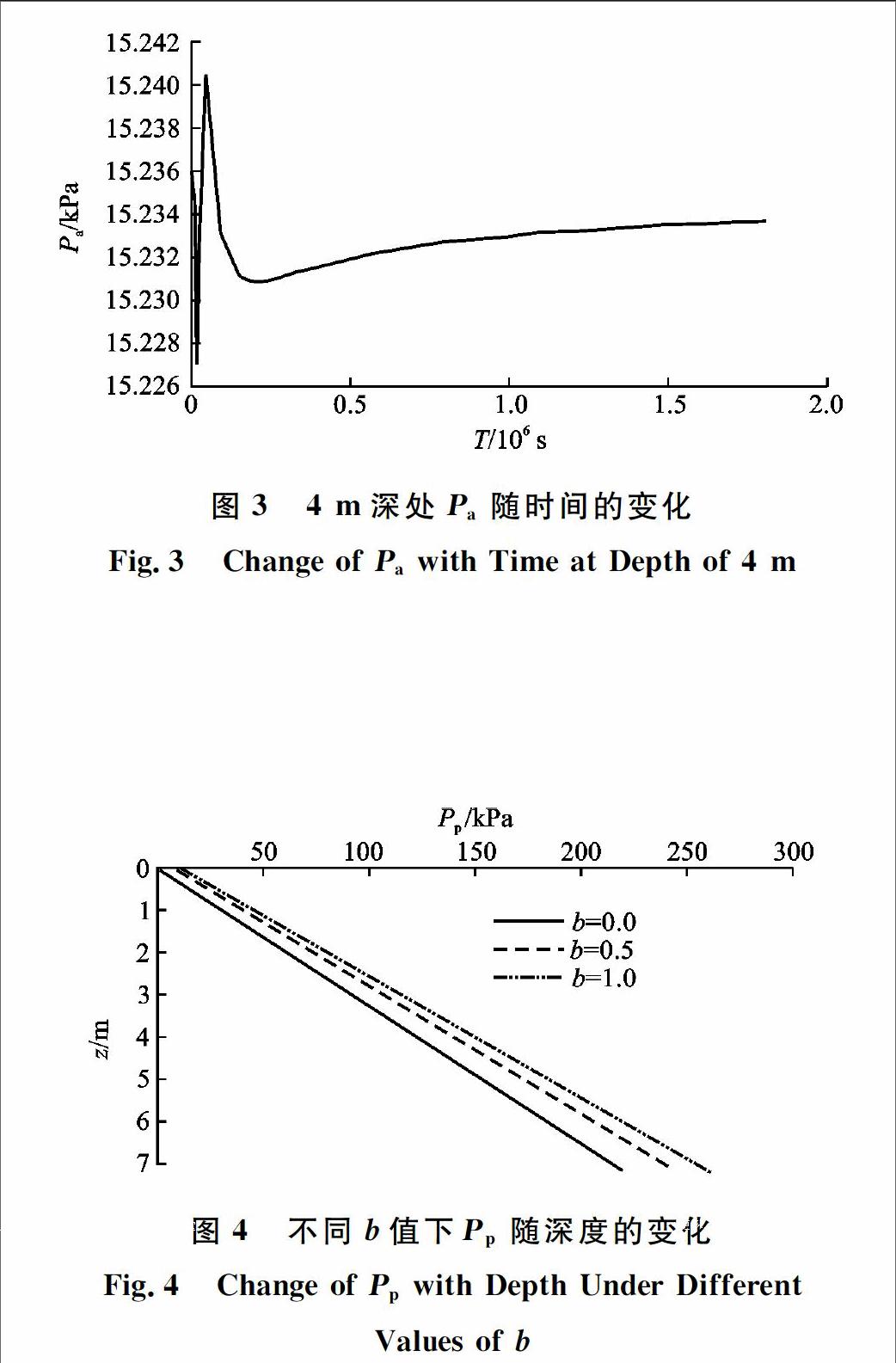
摘要:基于统一强度理论和Bishop有效应力原理,结合降雨入渗解析解,推导了考虑中间主应力效应及材料拉压比影响的降雨条件下非饱和朗肯土压力的统一解。通过算例验证了推导公式的有效性,并探讨了降雨条件下基质吸力的变化对非饱和土压力的影响。结果表明:主动土压力随着统一强度理论参数的增大而减小,而被动土压力呈现相反趋势;随着降雨的发生、浸润和停止,主动土压力和被动土压力呈现不稳定变化,最终都趋于稳定,这是由基质吸力的变化所引起的;非饱和渗透特征参数的选取会对土压力的计算产生显著影响。
关键词:非饱和土;降雨入渗;统一强度理论;基质吸力;土压力
中图分类号:TU432文献标志码:A
Abstract: Based on the unified strength theory and the principle of effective stress of Bishop, combining with rainfall infiltration analytic solution, the unified solution of Rankines earth pressure formula of unsaturated soil under rainfall condition was established with taking the effect of the intermediate principal stress and material tensionpressure ratio into account. The availability was verified by an example, and the influence of matric suction during rainfall was discussed. The results indicate that with the increase of the unified strength theory parameters, the active earth pressure decreases, whereas the passive earth pressure shows the opposite trend. In the wake of the occurrence, infiltration and end of rainfall, the earth pressure presents a tendency of unstable variation but finally stabilizes, which is caused by the change of matric suction during rainfall. The parameter of soil permeability character will significantly influence the earth pressure.
Key words: unsaturated soil; rainfall infiltration; unified strength theory; matric suction; earth pressure
0引言
自然界中的土是由土颗粒和颗粒间隙组成的,而现实土体中既存在空隙,也存在孔隙水,故工程中的地基土体大多为非饱和土。非饱和土在现实中分布非常广,多存在于半干旱和干旱地区地表周围土体中,除此之外非干旱地区的许多土体如人工填土、土坝、路基填土等也都处于非饱和状态。目前关于饱和土压力的计算理论较多,而关于非饱和土压力计算的研究却很少,其中比较有代表性的如:姚攀峰等[1]通过广义朗肯土压力公式得出土的原位指标与试验指标的关系,张健等[2]通过广义胡克定律将材料泊松比引入朗肯土压力计算中,张常光等[3]结合统一强度理论推导了非饱和土抗剪强度及土压力统一解。基质吸力在非饱和土压力计算中很关键,当基质吸力随外界条件变化时,土压力因基质吸力的变化也会发生相应的改变。在自然界中,降雨、侵润、蒸发等很多因素都可能引起土体干湿变化,从而引起基质吸力及土压力的变化。降雨入渗是典型的非饱和流固耦合现象[45],分析降雨条件下非饱和土压力时,雨水的瞬态渗流场、吸应力分布的变化、土体极限平衡状态等要素都必须考虑,然而现有非饱和土压力解多数未考虑降雨的影响。Fredlund双应力状态变量公式[6]和Bishop有效应力抗剪强度公式[7]是当前应用较广且较为成熟的非饱和土抗剪强度理论,仅从非饱和土抗剪强度看,2个理论公式的物理概念基本相同,不同点仅在于分别采用了吸力角φb和有效应力参数χ两种不同的参数形式[8]。Bishop由于参数χ取值考虑因素众多,可以使计算更精确。文献[9]将非饱和土力学理论与降雨渗流理论相结合,得出降雨入渗下非饱和朗肯土压力解,并与饱和土压力进行比较,但是未考虑中间主应力效应,计算结果偏于保守,不能充分利用土体的强度潜能。统一强度理论[1011]考虑了中间主应力的影响,适用于金属、岩石、土、混凝土、铸铁等应用十分广泛的材料,因此逐渐被用于各个领域。本文以现有的饱和土压力及非饱和土理论为基础,在Bishop有效应力原理和统一强度理论的基础上,结合降雨入渗解析解,探讨降雨条件下非饱和朗肯土压力计算,通过算例验证了推导公式的有效性并与传统非饱和朗肯土压力计算方法进行比较,分析土压力随时间及深度的变化。
1统一强度理论
当c,φ为已知量时,ct,φt为考虑了中间主应力σ2对材料屈服影响的新参数,且仅是统一强度理论参数b的函数。参数b和m分别从对材料屈服或破坏的影响程度和中间主应力的大小2个不同方面来体现中间主应力效应。2非饱和土的抗剪强度
可以看出:当n一定时,α在0.01~0.05范围内取值时,土压力变化较为明显,在0.05~0.1范围内时,土压力较为稳定;当α一定时,n在2~3范围内取值时,土压力变化较为明显,在3~4范围内时,土压力较为稳定。由此可见,在非饱和渗流计算中,非饱和渗透特征参数的选择对于非饱和土压力的计算也会产生很大影响。

