变换参考系解二体问题
——以2014年北约自主招生一道物理题为例
变换参考系解二体问题
——以2014年北约自主招生一道物理题为例
王 勇
【题目】真空中质量分别为m1和m2的两个小球,只受万有引力作用,某个时刻两个小球相距l0,小球1的速度为v0,方向指向小球2,小球2的速度为v0,速度方向垂直两球球心的连线,问若m1=m2=m0,当速度v0满足什么条件时,两小球的间距可以为无穷远?
解法1:惯性参考系法(质心参考系)
解题思路:寻找惯性参考系,分析两小球相对于惯性参考系的受力,确定两小球在惯性参考系的运动特点,直接运用牛顿运动定律或能量守恒求两小球相对惯性参考系的位移.
两小球组成的系统不受外力,质心做匀速直线运动,以质心为惯性参考系.
方法1:小球1距质心
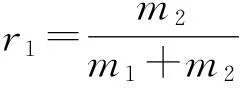
质心的速度
小球1相对于质心速度为
方向如图1所示.
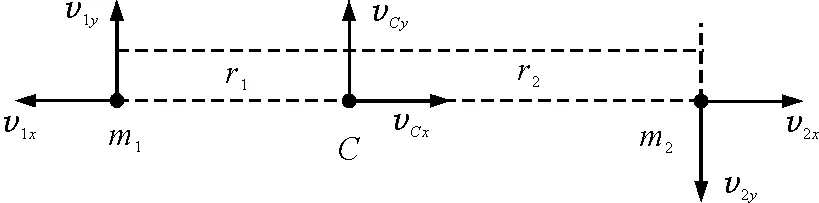
图1
小球1受力
在质心参考系中可认为小球1受到固定在质心处等效质点3的万有引力作用,等效质点3的质量
在受到与距离平方成反比的有心力作用下小球1将做圆锥曲线运动.同理可知小球2的运动.
由于小球1到质心的距离与两小球之间的间距成比例,当两小球相距无穷远时,即小球1距质心(等效质点3)无穷远,根据能量守恒,减小的动能转化为增加的势能,有
代入v1x,v1y,m3,r1与r的比例关系可得
当v1=v2=v0,m1=m2=m0,r=l0则

在质心参考系中根据能量守恒,有
代入v1x,v1y,v2x,v2y,m3,r1与r的比例关系同样有
解法2:非惯性参考系法
解题思路:以另一小球为非惯性参考系引入惯性力,分析小球相对非惯性系中受力,确定小球相对于非惯性系的运动特点,转化后运用牛顿运动定律或能量守恒求小球相对于非惯性系的位移.
方法1:以小球2为非惯性参考系,小球1受力
其中
则
小球1受到与距离平方成反比的有心力作用,将以小球2为中心做圆锥曲线运动,中心质点的等效质量为m1+m2.
根据能量守恒,减小的动能转化为增加的势能,有
其中小球1相对于小球2的相对速度为
代入v12同样有
方法2:以小球2为非惯性参考系,以小球1为研究对象根据牛顿运动定律有
F+m1a2=m1a12
其中
则
在只有万有引力的作用下小球1相对于固定不动小球2做圆锥曲线运动,小球1的等效质量为
根据能量守恒,减小的动能转化为增加的势能,有
代入m′,v12同样有

(收稿日期:2015-10-16)
*作者简介:王勇(1978-),男,中教高级,主要从事物理竞赛教学与研究.
(常州高级中学江苏 常州213000)
——兼谈参考系与坐标系的关联关系

