硒化钨拉曼光谱层数效应

杨学弦，张峰，刘理军，廖文虎，刘永辉，莫贤通，冯晶

(1.吉首大学 物理与机电工程学院，吉首　416000;2.湘潭大学 材料科学与工程学院，湘潭　411105)



硒化钨拉曼光谱层数效应

杨学弦1，张峰1，刘理军1，廖文虎1，刘永辉2，莫贤通1，冯晶1

(1.吉首大学 物理与机电工程学院，吉首416000;2.湘潭大学 材料科学与工程学院，湘潭411105)

摘要:应用键弛豫理论(BOLS)对层状硒化钨材料的拉曼光谱进行定量分析，得出了硒化钨层数与键参数的数值函数关系。澄清了硒化钨拉曼频移层数效应的内在起因：硒化钨层数增加时，拉曼振动模A1g发生蓝移是由于最近邻原子的影响；成键原子控制着硒化钨拉曼模和模的红移。

关键词：层数；二硒化钨；拉曼频移；有效配位数

1引言

二硒化钨,由二维Se-W-Se 的层状结构构成，层内通过共价键结合,而层间通过范德瓦尔斯结合。大量实验研究表明[1-3],硒化钨薄膜的电子和声子性质具有显著的层数效应：二维纳米硒化钨薄膜厚度减小到单层时,能带结构会从间接带隙过渡到直接带隙；声子谱将随着层数的减少而发生红移或蓝移现象。由于拉曼散射实验(拉曼散射实验：不破坏样品，无损检测且结合计算机技术可达到实时实地的表征)能够较精确地表征薄膜的层数与电子和声子间的关系，因此常选择拉曼散射实验对二硒化钨的层数效应进行表征[4]。

2键弛豫理论

局域键平均近似[10]：对于任意样品，无论是晶体、非晶体、完整或者有缺陷的，只要不发生相变其化学键性质和总数保持不变。而当外界环境发生变化时，样品所有的化学键键长和键能都会随之产生响应。因此，可通过样品化学键参数与外界环境间的联系对材料性能进行研究。

键弛豫理论(BOLS)[7]：低配位原子(z)的化学键键长自发收缩变短，键能增强。 BOLS理论数学表达[11-12]：

(1)

其中下标z表示有z个最近邻有效配位数；b表示块体值；Cz为键收缩系数，仅仅是有效配位数的函数。d表示化学键键长；m表示键性质参数；E表示原子结合能。

3层数与拉曼光谱

通过泰勒级数对原子总能量进行展开，可得到[13]：

(2)

E(d，T)表示z个配位数的某原子总能量，T、d和u(r)分别是温度、键长和势能，EB为零温下原子间键能，约化质量μ=m1m2/(m1+m2)，ω(0)是零温零压下拉曼光谱频率。从能量的角度分析，任何外界条件都将引起原子键能的改变从而导致原子振动频率的变化。

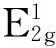
Δωx(z,dz,Ez,μ)=

ωx(z,dz,Ez,μ)-ωx(1,dz,Ez,μ)=

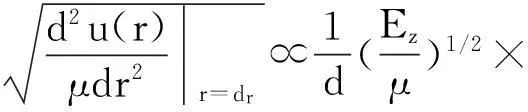
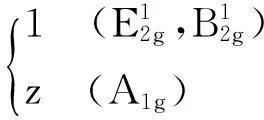
(3)

在此可通过获取低维层状材料拉曼效应不同模式的实验测量结果，对比其变化趋势来证明这一假定的正确性。

合并式(1)和(3)，以块体硒化钨有效配位数Zg=12作为已知参数，可得到以下三种拉曼振动模式的关系式：

配位数与相对拉曼频移的函数关系式：

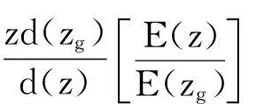
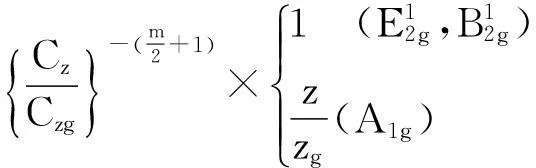
(4)

参考点频率与配位数的一般表达式：

(5)

拉曼振动频率与配位数的函数关系式：

w(z)=wx(1)+

[wx(zg)-wx(1)]Ax(z,zg)

(6)

4结果与讨论

(7)

(9)

硒化钨拉曼频移与配位数的函数关系式：

(10)

(11)

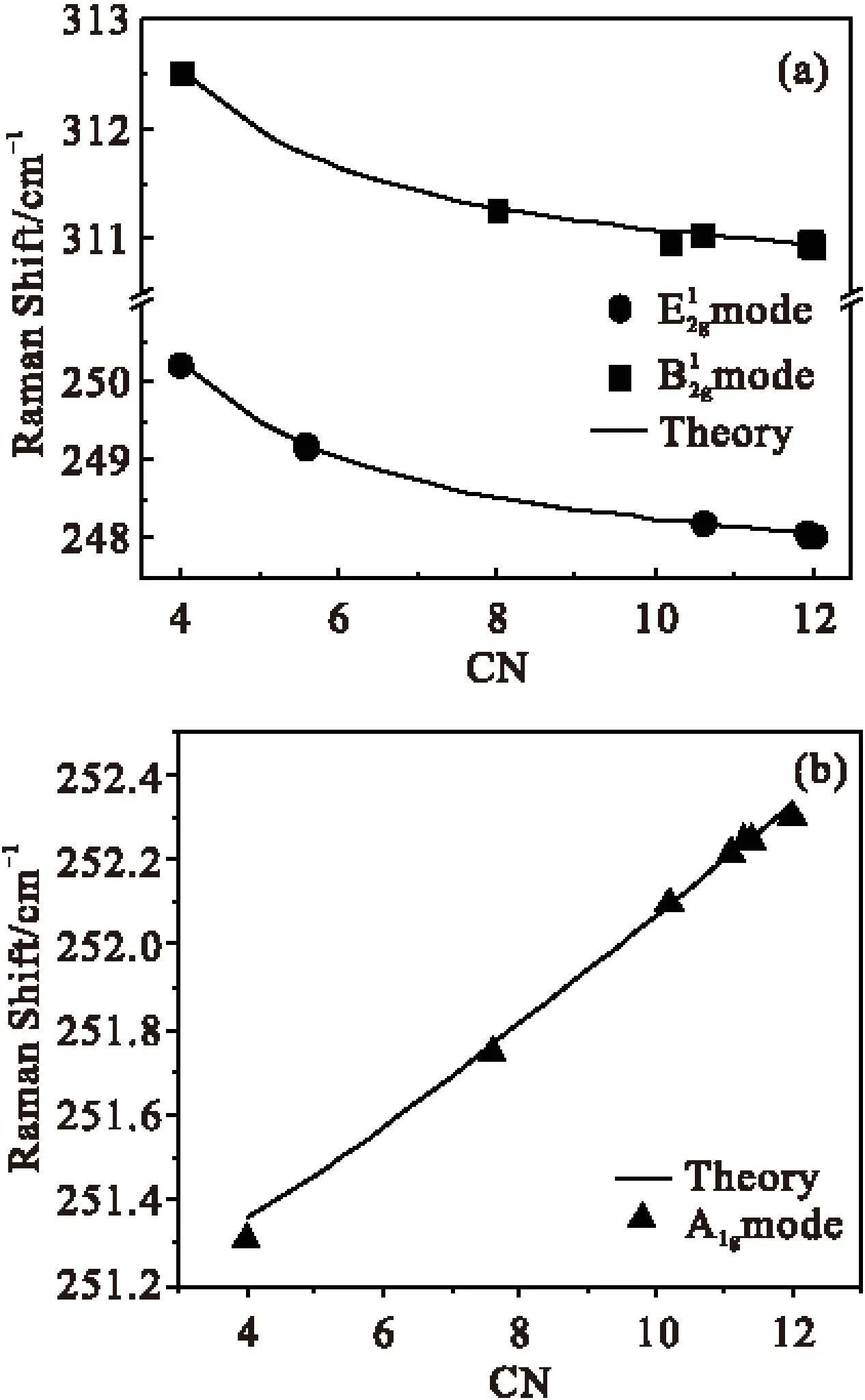
图2是通过理论计算单/多层二硒化钨拉曼频移与配位数的结果图a、b与已知实验测量的拉曼频移与层数的关系，衍生出的配位数与层数的关系。从图中可以发现，随着层数的增加，有效原子配位数与层数之间成线性增加的关系，近似满足等式：Z=1.16+2.26n(n<5)，Z代表配位数，n代表层数。

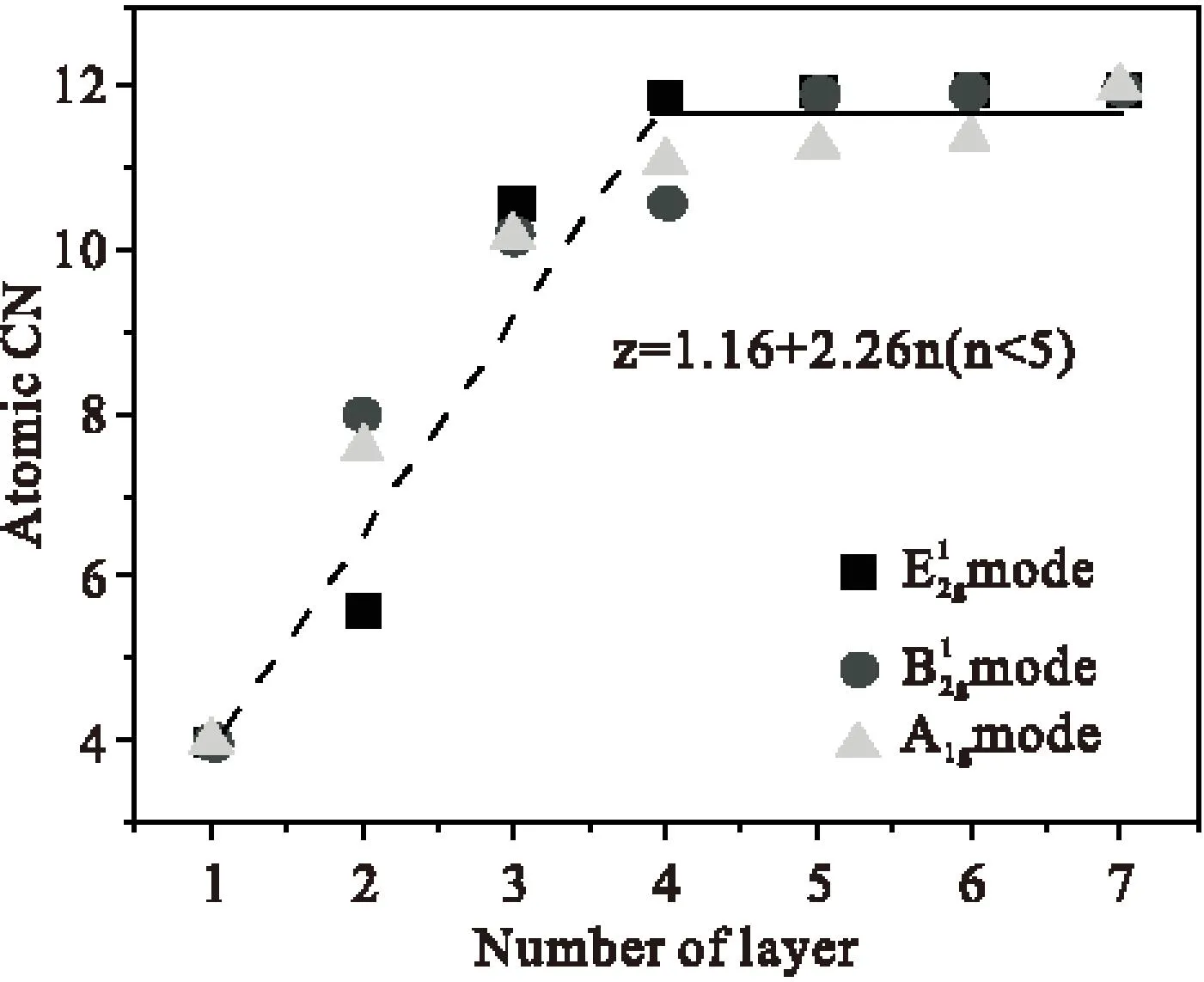
Fig.2Effective atomic coordination number of CN (z) of the relationship between the WSe2layers N and two Se.From the figure can be found,with the increase of layers,the effective atomic coordination number is increasing

5结论

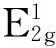
参考文献

[1]Zeng H L,Liu G B,Dai J F,etal.Optical signature of symmetry variations and spin-valley coupling in atomically thintungsten dichalcogenides [J].Sci Rep,2013,3:1608-1-4.

[2]Zhao W J,Ghorannevis Z,Chu L Q,etal.Evolution of electronic structure in atomically thin sheets of WS2and WSe2[J].ACS Nano,2013,7(1):791-797.

[3]Yun W S,Han S W,Hong S C,etal.Thickness and strain effects on electronic structures of transition metal dichalco-genides:2H-MX2semiconductors (M = Mo,W; X = S,Se,Te) [J].Phy Rev B,2012,85(3):033305-1-4.

[4]胡晓红,周金池.拉曼光谱的应用及其进展[J].分析仪器,2011(06) ；1-4(Hu Xiaohong,Zhou Jinchi.The application and progress of Raman spectrum[J].Analytical Instrument,2011(06);1-4.)

[5]Luo X,Zhao Y Y,Zhang J,etal.Effects of Lower Symmetry and Dimensionalityon Raman Spectra in 2D WSe2[J].Phys Rev B,2014,88(19):293-298.

[6]Sun C Q,Bai H L,Tay B K,etal.Dimension,strength,and chemical and thermal stability of a single C-C bond in carbon nanotubes [J].J Phys Chem B,2003,107(31):7544-7546.

[7]Sun C Q.Size dependence of nanostructures:Impact of bond order deficiency [J].Progress in Solid State Chemistry,2007,35(1):1-159.

[8]Zhang X,Zheng W T,Kuo J L,etal.Discriminative generation and hydrogen modulation of the Dirac-Fermi polarons at graphene edges and atomic vacancies [J].Carbon,2011,49:3615-3621.

[9]Sun C Q,Sun Y,Nie Y G,etal.Coordination-Resolved C-C Bond Length and the C 1s Binding Energy of Carbon Allotropes and the Effective Atomic Coordination of the Few-Layer Graphene [J].J Phys Chem C,2009,113(37):16464-16467.

[10]Sun C Q.Thermo-mechanical behavior of low-dimensional systems:The local bond average approach [J].Prog Mater Sci,2009,54(2):179-307.

[11]Yang X X,Li J W,Zhou Z F,etal.Frequency response of graphene phonons to heating and compression [J].Appl Phys Lett,2011,99(13):133108-133112.

[12]杨学弦.碳同素异构体碳-碳键弛豫动力学的计量拉曼谱研究[D].湘潭大学 2013.(Yang Xuexian.Quantitative Raman Spectroscopes of C-C Bond Relaxation Dynamics in Carbon Allotropies[D].Xiangtan University,2013)

[13]Sun C Q,Pan L K,Li C M,etal.Size-induced acoustic hardening and optic softening of phonons in InP,CeO2,SnO2,CdS,Ag,and Si nanostructures[J].Physical Review B,2005.72(13).134301.

[14]Yang X X,Zhou Z F,Wang Y,etal.Raman spectroscopy determination of the Debye temperature and atomic cohesivenergy of CdS,CdSe,Bi2Se3,and Sb2Te3nanostructures [J].J Appl Phys,2012,112,4759207.

Raman Spectrum Effect of Layer-W

Se2YANG Xue-xian1,ZHANG Feng1,LIU Li-jun1,LIAO Wen-hu1,LIU Yong-hui2,MO Xian-tong1,FENG Jing1

(1.JishouUniversity,CollegeofPhysics,MechanicalandElectricalEngineering,Jishou416000;2.XiangtanUniversity，SchoolofMaterialsScienceandEngineering，Xiangtan411105)

Abstract:From the perspective of bond order-length-strength correlation and the local bond averaging approach,we have formulated the number-of-layer resolved Raman shifts of WSe2,with quantification of the referential origins from which the Raman shifts proceed and clarification of their origins.It is found that the primary mode and mode are dominated by the interaction between a specific atom and its nearest neighbors while the A1gmode by the dimer interaction,and therefore red shift happens to the phonons and blue shift to the A1gmode upon the number-of-layer is reduced.

Key words:layer; WSe2; Raman shift; effective coordination number

中图分类号：O433.4

文献标志码：A

doi:10.13883/j.issn1004-5929.201601004

作者简介：杨学弦(1984-)，男，讲师，主要从事声子计量谱学等方面的研究。E-mail:yangxuexiand@163.com

基金项目：国家自然科学基金( 11447237)，湖南省自然科学基金(2015JJ6094) 资助项目

收稿日期：2015-07-01; 修改稿日期:2015-07-21

文章编号：1004-5929(2016)01-0012-04