带隔板线型聚能装药侵彻能力的正交优化

徐景林， 顾文彬， 武双章， 黄 鹤， 王振雄

(解放军理工大学 野战工程学院， 南京 210007)



带隔板线型聚能装药侵彻能力的正交优化

徐景林， 顾文彬， 武双章， 黄 鹤， 王振雄

(解放军理工大学 野战工程学院， 南京 210007)

摘要：为了获得带隔板线型聚能装药最佳的结构参数，采用正交优化设计的方法，研究了药型罩楔形角2α、壁厚δ、装药高度H、隔板宽度a、隔板楔形角2β 5个因素对线型聚能射流的影响，选取L25(55)正交优化表，利用LS-DYNA软件进行仿真计算，得到了5个因素对射流最大速度和射流长度影响的主次顺序，描述了各因素对射流两个指标的影响规律，获得了最佳的结构组合a3-2β2-H5-2α4-δ4。实验证明，该装药结构对钢靶的侵彻深度大于1倍药型罩口宽，提高了线型聚能装药的切割能力。

关键词：隔板； 药型罩； 线型聚能装药； 正交优化； 侵彻深度

1引 言

近年来，对于线型聚能装药的研究已经日趋成熟，与传统的锥形聚能装药相比，它能够对目标造成长条形的切口，广泛应用于宇航、军事、工业等各种领域，如导弹、运载火箭等的自毁系统与分离装置，军事飞机的座椅弹射系统、水下沉船的解体打捞、钢建筑结构物的拆除等〔1-5〕。为了实现对某些大型坚固结构的爆破切割，武双章等〔1〕设计了一种大口宽、大装药量的线型切割器，分别对楔形和椭圆形药型罩结构的线型聚能装药进行了优化，获得了良好的切割效果。在传统的锥形聚能装药中经常使用隔板来改变爆轰波形，从而提高侵彻能力。借鉴这一思路，本文设计了一种带隔板的线型聚能装药结构，能使射流头部速度有较大程度的提高，切割的效果明显增强。

正交优化法是利用正交表来对试验方案进行整体设计、综合比较、统计分析，通过少量的实验找到较好的方案，能够在因素变化范围内均衡抽样，使每种方案都具有较强的代表性。本文采用正交优化的方法对带隔板线型聚能装药结构中影响射流成型和侵彻的因素进行研究，获得优化方案。

2隔板理论研究

2.1隔板对线型聚能装药的影响

在线型聚能装药中添加隔板，装药起爆以后，爆轰波绕过隔板传播，对药型罩的初始作用角减小，这是带隔板线型聚能装药射流速度要优于不带隔板线型聚能装药的根本原因，爆轰波形与药型罩的外形越接近，形成的射流速度就会越高〔6〕。隔板对爆轰波的影响过程，如图1所示。

图1　隔板对爆轰波传播的影响Fig.1　The influence of wave-shaper on detonation wave propagation

当有隔板时，爆轰波首先绕过隔板，然后朝向药型罩传播，结果在爆轰波绕过隔板到达药型罩之前可能形成不同的形状，在这种情况下爆轰波作用于药型罩，波阵面与罩表面的夹角为φ1；当没有隔板时，爆轰波以球面波的形式向药型罩传播，波阵面与罩表面的夹角为φ2，可以看出φ1<φ2。理论分析与实验结果表明，作用在药型罩上的初始压力与φ有很大关系，这个关系近似表达为〔7〕：

Pm=PCJ(cosφ+0.68)

(1)

式中：Pm为装药起爆后爆轰产物作用在罩面上的初始压力；PCJ为炸药的爆轰压力，MPa。

采用隔板后，φ会变小，作用于罩面的初始压力Pm随之增加。

2.2射流成型的影响因素分析

(1)隔板宽度和楔形角

爆轰波绕过隔板后波阵面是多样化的，波形很大程度上取决于隔板的形状，如隔板的宽度、楔形隔板的角度等，不同的隔爆体对波形的影响很大。在轴对称装药中，隔板最佳直径约为0.8倍装药口径〔8〕，这为LSC中隔板宽度的选取提供了参考。

楔形隔板的角度决定了隔板的厚度，角度过大使得隔板厚度变薄，隔爆效果不佳；角度过小会增加装药高度和装药量。

(2)药型罩楔形角与壁厚

从实践和理论研究中，都可以得出〔9〕：

(2)

式中：α为药型罩半顶角；θ为微元偏转角。

最佳罩半顶角α由偏转角θ决定，对于线型切割器，其装药质量比(装药质量与药型罩质量之比)R取值范围是1.5~4.0，根据泰勒角公式，得到偏转角θ=15°~20°，代入式(2)可以得到2α=80°~100°。

药型罩壁厚对射流的形成有很重要的影响，影响射流速度和射流的长度，药型罩厚度越大，药型罩转化为射流的质量就会增加，但同时也会导致初始射流速度降低。壁厚太厚有可能不形成射流而产生碎片；壁厚太薄，虽然射流速度增加，但是射流质量减小，对侵彻效果不利，为了方便研究减少变量，采用等壁厚的楔形药型罩。

(3)装药高度

聚能装药高度会影响射流的侵彻能力，随着装药高度的增加，侵彻深度增加，一般呈线性关系。考虑到装药量过大会造成很大的破坏效应，所以隔板到药型罩顶端装药高度不大于40mm；隔板与药型罩顶端的距离会影响在轴线碰撞后爆轰波的进一步成长。模拟中发现，当距离小于20mm时，会使药型罩进入杵体的质量增加，而形成射流的质量减小，射流在较短的时间内断裂，因此装药高度应在20mm~40mm内选取。

3各因素水平选择

根据前述装药结构优化分析，确定了隔板宽度a、隔板楔形角2β、隔板到药型罩顶端装药高度H、药型罩楔形角2α、壁厚δ共5个变量作为正交优化的因素，不考虑各因素之间的交互作用，确定每个因素等间隔选取5个水平值。所以带隔板线型聚能装药结构的参数优化归结为5因素5水平正交优化问题，各因素水平取值如表1所示。

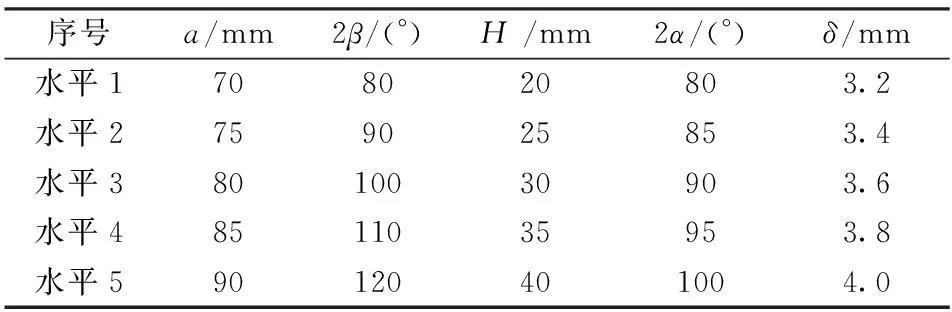
表1　正交优化各因素水平

4数值模型的建立

模型由炸药、药型罩、隔板和空气四部分组成，采用欧拉网格建模，单元使用多物质ALE算法。模型采用单层实体网格，并在长度方向的断面上施加约束，使用三维实体材料模型，这样既可以准确描述线型射流的特点，又可以大大减少计算时间。由于线型聚能装药结构是面对称结构，所以只建立对称面一侧的1/2模型，装药结构如图2所示，药型罩口宽96mm，两边分别包上2mm厚炸药，装药宽度为100mm，起爆方式采用“顶部中心起爆”。

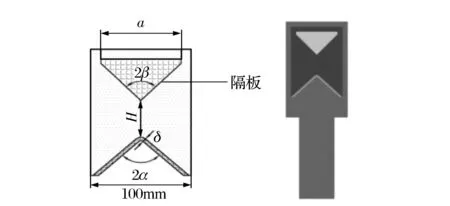
图2　带隔板线型聚能装药结构与数值模型Fig.2　The structure and numerical model of LSC with wave-shaper

材料模型和参数的选择很大程度上决定着模拟的结果是否准确，根据前期数值模拟和实验工作，炸药选择聚能装药常用的B炸药，密度1.717g/cm3，爆速7980m/s，采用High Explosive Burn本构模型及JWL状态方程。纯铁在通常条件下是脆性材料，但在高温、高压条件下呈现很好的塑形特性，因此选为药型罩材料，通过Johnson-cook材料模型来描述，所用材料的状态方程为Grüneisen方程。隔板选用聚氨酯材料，它密度小，具有良好的吸收爆炸冲击能量的效果，采用Elastic Plastic Hydro材料模型，选用Grüneisen状态方程，聚氨酯〔10〕密度0.12g/cm3，弹性模量17.67MPa，屈服强度1.0602MPa。

5正交优化结果

根据射流侵彻理论，聚能装药所形成的射流，其头部速度越高、射流越长越有利于侵彻，于是将形成有利射流的条件约束为较高的射流头部速度和较大的射流长度，并将其作为评价指标，各方案的计算结果见表2。

对计算结果采用极差分析的方法进行研究：将各列水平数相同的计算结果相加除以5，得到各水平的平均计算结果，记为k1，k2，k3，k4，k5，用每个水平的最大值减去最小值即得到各因素的极差R，根据每个极差R的大小可以确定每个因素对两个指标影响的重要程度。射流最大速度v和射流长度l的极差分析表见表3。

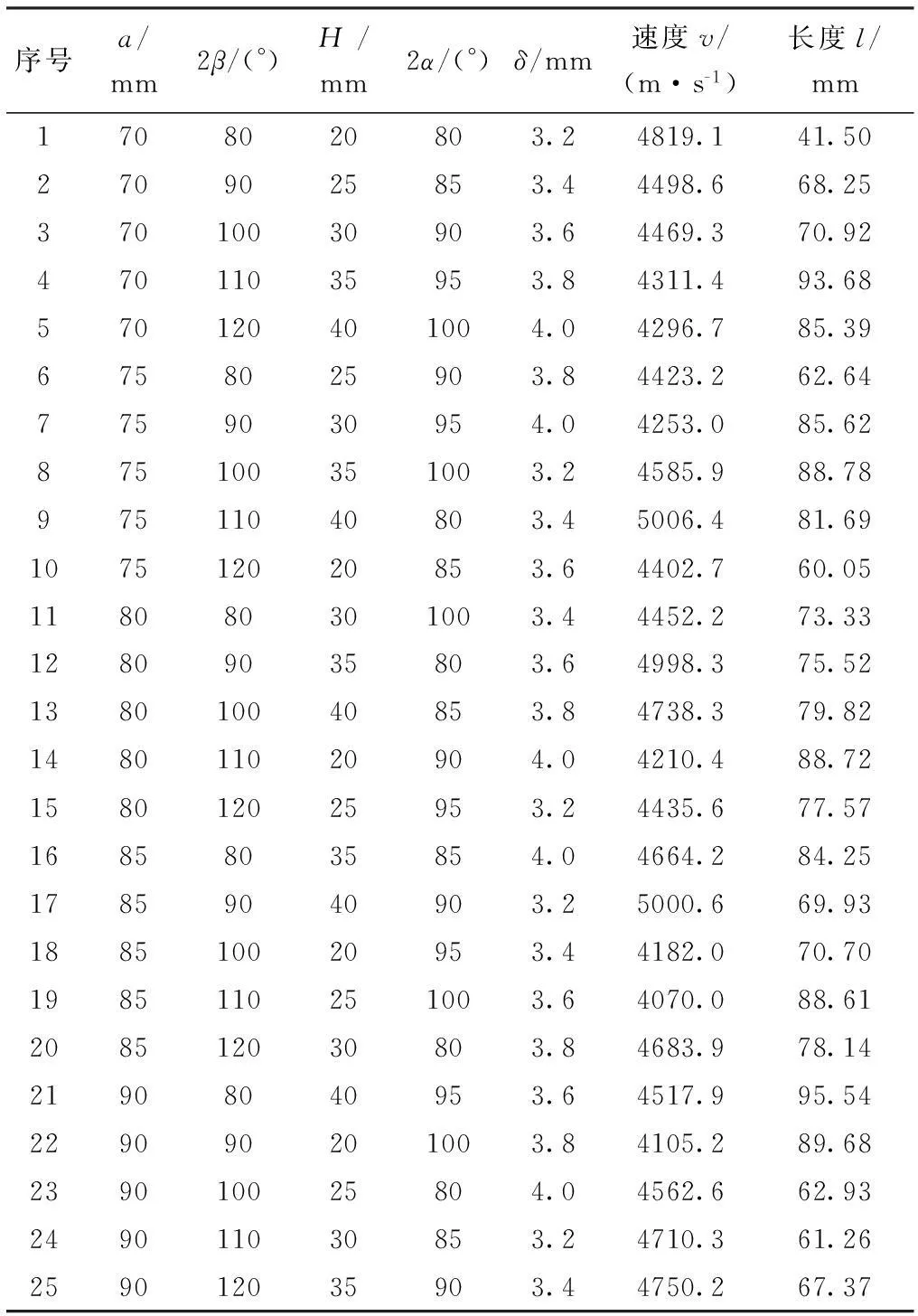
表2　正交优化方案表及计算结果

由极差分析结果可以看出，各因素对射流最大速度(v)的影响的重要程度2α> H > δ > 2β> a，对射流长度(l)影响的重要程度2α> δ > H > a > 2β。2α是影响v和l的最重要因素,H是影响v的第二重要因素，同时也是影响l的第三重要因素；δ是影响v第三重要因素和l的第二重要因素，这三个因素是影响射流指标的主要因素。a和2β对v和l的影响相对较小。

射流头部最大速度随着各因素的变化趋势如图3所示。从图中可以看出，射流最大速度随着药型罩楔形角的增大而减小，随着H的增大而增大，随着药型罩壁厚的增大而减小，随着隔板宽度的增加，射流头部速度先增大后减小，第三水平时最大，随着隔板楔形角的增大而减小。选取各因素使射流头部速度达到最大的方案作为第一种优化方案，即：a3-2β1-H5-2α1-δ1。

表3　射流指标极差分析

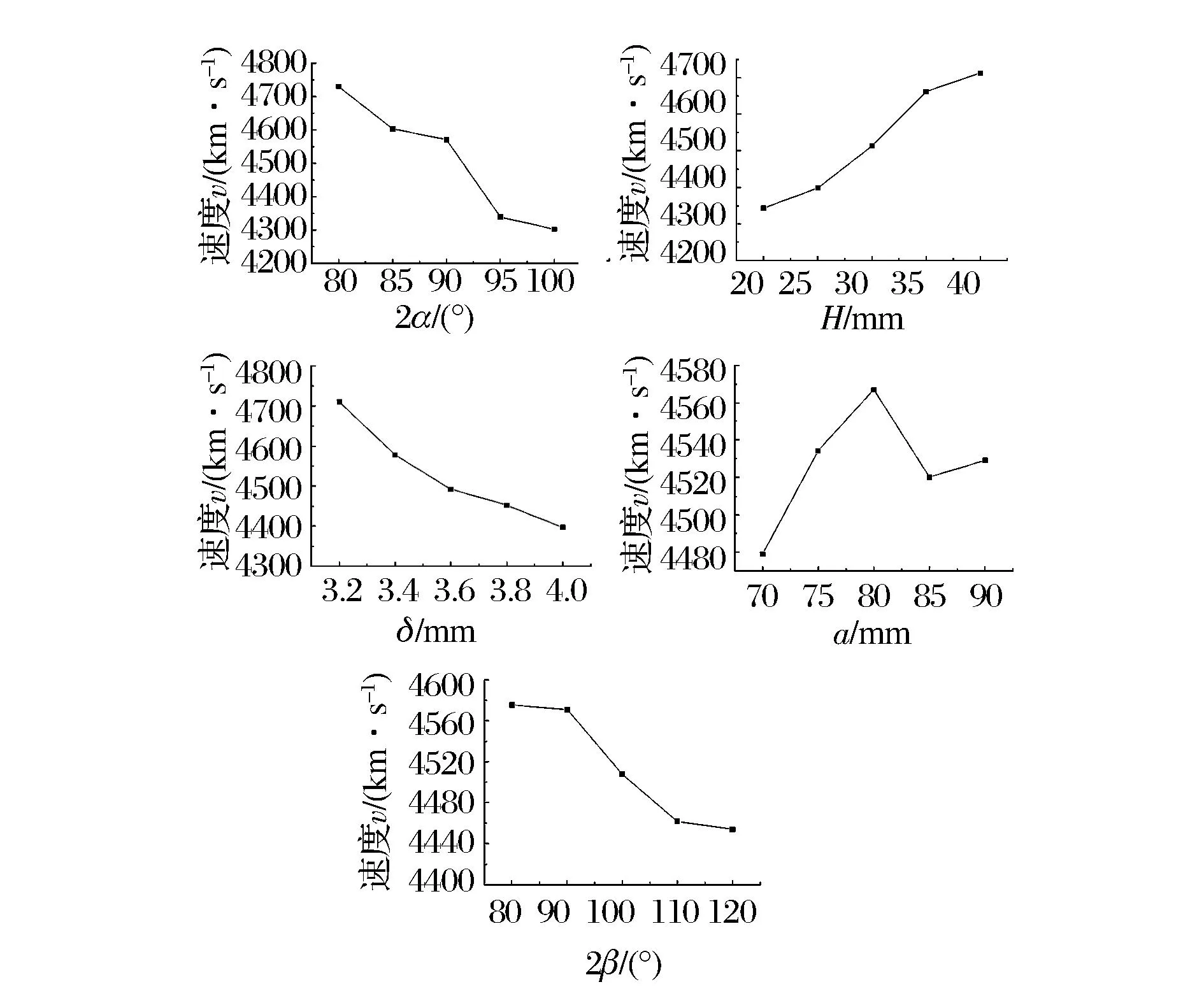
图3　射流最大速度受各因素影响的分布趋势Fig.3　The trend of the jet maximum velocity affected by five factors

射流长度随着各因素的变化趋势如图4所示。从图中可以看出，射流长度随着药型罩楔形角的增大而增大，随着H的增大而增大，随着药型罩壁厚的增大而增大，随着隔板宽度的增加， 先增大后减小，第三水平时最大，随着隔板楔形角的增大先增大后减小，第二水平最大。选取各因素使射流长度达到最大的方案作为第二种优化方案，即：a3-2β2-H5-2α5-δ5。

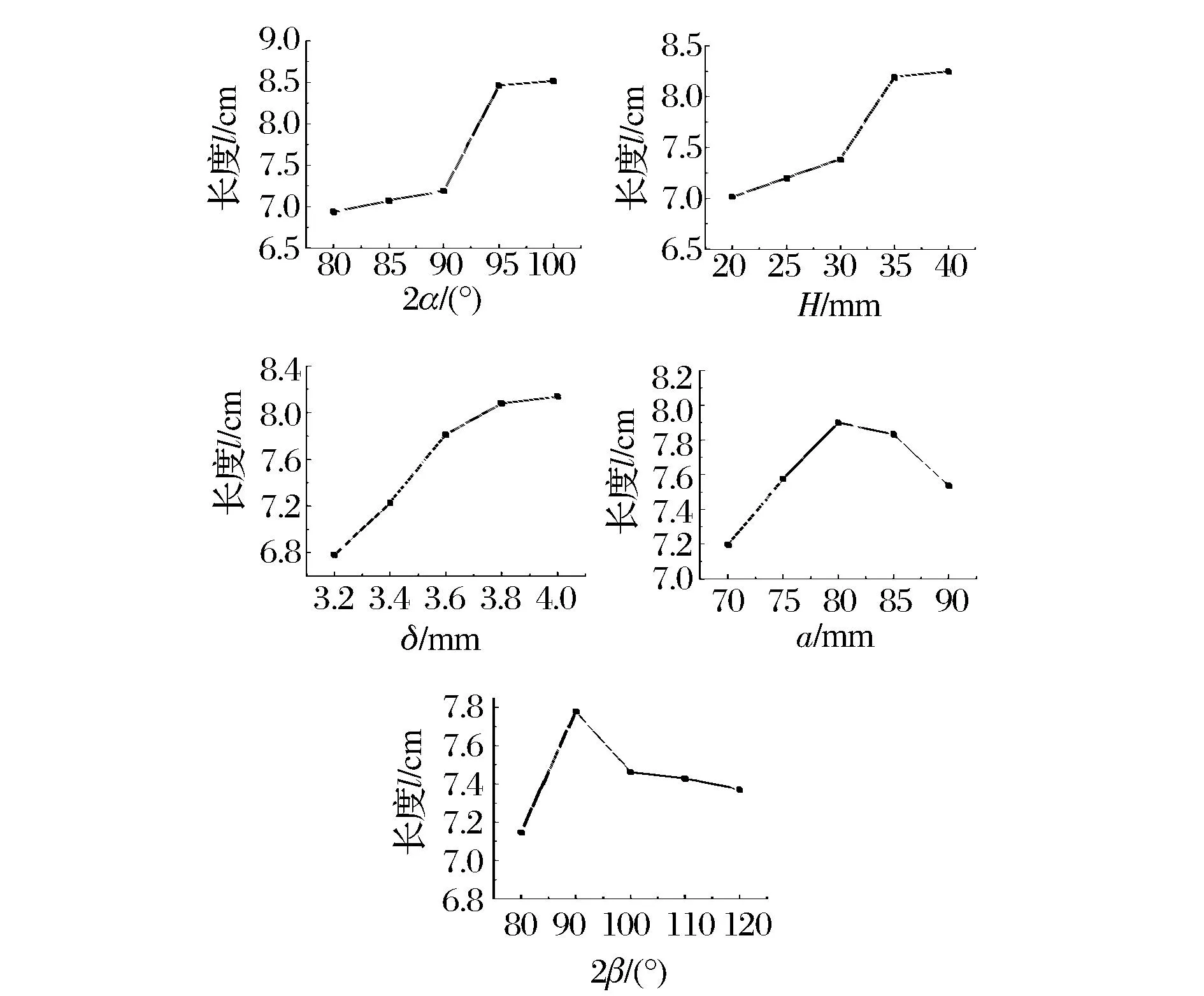
图4　射流长度受各因素影响的分布趋势Fig.4　The distribution trend of jet length affected by five factors

综合考虑各因素对两个指标的影响，可以看出药型罩楔形角选取第四水平95°时，虽然头部最大速度比前三水平有所下降，但是是射流长度增加较多；H选择第五水平40mm，此时两指标都是极大值；δ较小时，虽然射流头部速度很大，但是射流长度很短。δ=3.8mm时，头部速度较大，射流长度相比其它罩厚度提高很多，所以选取δ=3.8mm；隔板楔形角的影响较小，选择第二水平90°，此时射流长度最大，射流速度也是较大值；隔板宽度a=80mm时，两指标都是极大值，所以第三种优化方案是a3-2β2-H5-2α4-δ4。

对三种优化方案进行了不同炸高下侵彻钢靶的数值模拟，计算结果如表4所示。可以看出第三种方案明显优于前两种优化方案，所以选取第三种优化方案作为最佳结构组合。

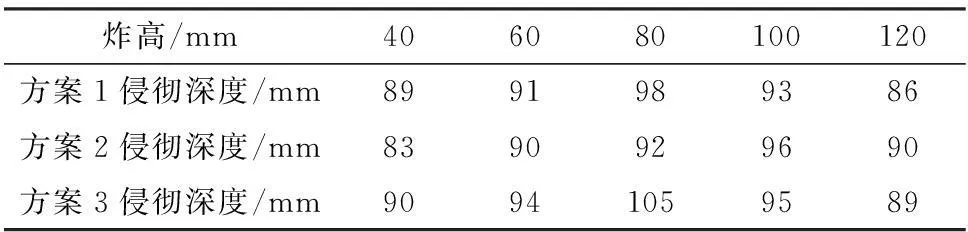
表4　优化方案计算结果

6试验验证

根据数值模拟计算结果，对最佳结构组合的线型聚能装药进行了80mm炸高下(0.8倍的装药宽度)切割钢锭的试验，其中装药长度为100mm，采用雷管在装药的顶部中心起爆，试验设置见图5。

图5　切割钢锭试验Fig.5　The experiment of cutting steel

试验过后收集切割的钢锭破片，试验前钢锭高度均为245mm，试验后钢锭的剩余高度如图5(b)所示。由此算出两次试验带隔板聚能装药的中心侵彻深度分别为102mm、91mm，平均侵彻深度96.5mm，数值计算侵彻深度是105mm，二者误差达到试验平均侵深的8.8%，所以数值模拟选取的模型参数可靠，计算结果与试验结果吻合较好。本次试验的药型罩底部宽度96mm，可见切割深度大于一倍药型罩口宽，切割效果较好。

7结 论

(1)对带隔板的线型聚能装药进行了正交优化，获得了隔板和药型罩等参数对射流特性影响的重要程度，对射流头部速度2α> H > δ > 2β> a，对射流长度2α> δ > H > a > 2β。

(2)射流最大速度随着药型罩楔形角2α的增大而减小，随着壁厚δ的增大而减小，随着隔板到药型罩顶端的距离H的增大而增大，随着隔板宽度a的增大先增后减，随着隔板楔形角2β的增大而减小；射流长度随着药型罩楔形角2α、壁厚δ、隔板到药型罩顶端的距离H的增大而增大，随着隔板宽度a、隔板楔形角2β的增大先增后减。

(3)通过正交优化获得了最佳的装药结构a3-2β2-H5-2α4-δ4，试验证明该结构对钢锭的侵彻深度大于一倍药型罩口宽，并且切断面整齐，达到了较好的切割效果。

参考文献(References)：

〔1〕武双章，顾文彬，尼志青，等.起爆方式对截底椭圆形罩LSC射流成型影响的三维数值模拟[J]. 工程爆破，2015,21(5)：47-53.

WU Shuang-zhang, GU Wen-bin, NI Zhi-qing, et al. Tri-dimensional numerical simulation on the influence of jet formation process of the LSC with cutting-bottom oval cover under different initiation modes[J]. Engineering Blasting, 2015,21(5)：47-53.

〔2〕 王飞，王连来，刘广初. 线性切割器正交优化设计与数值模拟研究[J]. 爆破器材,2006,35(2):23-26.

WANG Fei, WANG Lian-lai, LIU Guang-chu. Orthogonal optimization designation and numerical simulation of liner shaped charge[J]. Explosive Materials, 2006,35(2):23-26.

〔3〕 崔云航，万文乾，田七，等. 线性聚能装药优化设计[J]. 火工品, 2006(4): 42-46.

CUI Yun-hang, WAN Wen-qian, TIAN Qi, et al. Optimization design of liner shaped charge[J]. Initiators & Pyrotechnics, 2006(4):42-46.

〔4〕 马海洋，龙源，何洋扬. 炸高对线型聚能切割器切割深度影响的数值分析[J]. 火工品,2008(4):28-32.

MA Hai-yang, LONG Yuan,HE Yang-yang, et al . Numerical analysis on effects of burst height on penetration depth of LSCC[J]. Initiators and Pyrotechnics, 2008(4):28-32.

〔5〕 崔云航，李裕春，吴腾芳，等. 线型聚能装药数值模拟与优化设计[J]. 爆破,2005,22(3):26-29.

CUI Yun-hang, LI Yu-chun, WU Teng-fang，et a1. Numerical simulation and optimization design of linear shaped charge[J]. Blasting,2005,22(3):26-29.

〔6〕 王成，付晓磊，宁建国. 起爆方式对聚能射流性能影响的数值分析[J]. 北京理工大学学报，2006,26(5):401-404.

WANG Cheng, FU Xiao-lei, NING Jian-guo. Numerical simulation of shaped charge jet formation under different ways of initiation[J]. Transactions of Beijing Institute of Technology, 2006, 26(5): 401-404.

〔7〕 隋树元，王树山. 终点效应学[M]. 北京：国防工业出版社，2000：274-276.

SUI Shu-yuan, WANG Shu-shan. Terminal effects[M]. Beijing:National Defence Industry Press,2000：274-276.

〔8〕 李如江，张晋红，王建波. 隔板对聚能射流性能影响的数值模拟[J]. 弹道与制导学报,2012,32(3): 107-110.

LI Ru-jiang, ZHANG Jin-hong, WANG Jian-bo. Numerical simulation of the effect of wave-shaper on shaped charge jet′s performance[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2012, 32(3): 107-110.

〔9〕 张凯，李晓杰. 聚能线型切割器最佳张开角的理论分析[J]. 爆炸与冲击,1988,8(4): 316-322.

ZHANG Kai，LI Xiao-jie. Analysis of linear shaped charge angle[J]. Explosion and Shock Waves, 1988,8(4):316-322.

〔10〕石少卿，张湘冀，刘颖芳，等. 硬质聚氨酯泡沫塑料抗爆炸冲击作用的研究[J]. 振动与冲击,2005,24(5): 56-58.

SHI Shao-qing, ZHANG Xiang-ji, LIU Ying-fang,et al. Study of rigid polyurethane foamed plastic by explosion[J]. Journal of Vibration and Shock,2005,24(5): 56-58.

Orthogonal optimization of penetration ability of linear shaped charge with wave-shaper

XU Jing-lin， GU Wen-bin， WU Shuang-zhang， HUANG He， WANG Zhen-xiong

(Field Engineering Institute, PLA University of Science and Technology , Nanjing 210007， China)

ABSTRACT：To obtain the optimal structural parameters of linear shaped charge with wave-shaper, the method of orthogonal design was used to study five factors affect on LSC jet, including shaped charge liner wedge angle 2α, wall thickness δ, charge height H, wave-shaper width a and wave-shaper wedge angle 2β. L25 (55) orthogonal optimization table and LS-DYNA simulation software were chosen. The order of five factors impact on the jet speed and length were achieved. The influence of various factors on the two indicators of jet was described and the best combination of structure a3-2β2-H5-2α4-δ4 was obtained. The experiment showed that the maximum penetration depth of steel target was more than twice as much as mouth width of shaped charge liner, and the cutting ability of LSC was raised.

KEY WORDS:Wave-shaper; Shaped charge liner; Linear shaped charge; Orthogonal optimization; Penetration depth

中图分类号：TD235

文献标识码：A

doi：10.3969/j.issn.1006-7051.2016.01.017

作者简介：徐景林(1991-)，男，硕士，主要从事炸药爆炸及其应用方面的研究工作。E-mail: xjl4096@163.com

收稿日期：2015-12-30

文章编号：1006-7051(2016)01-0077-05