煤与瓦斯共采钻孔增透半径理论分析与应用

马念杰，郭晓菲，赵希栋，李　季，闫振雄

(中国矿业大学(北京) 资源与安全工程学院，北京　100083)



煤与瓦斯共采钻孔增透半径理论分析与应用

马念杰，郭晓菲，赵希栋，李季，闫振雄

(中国矿业大学(北京) 资源与安全工程学院，北京100083)

摘要:在煤与瓦斯共采时，受采动加、卸载应力影响，瓦斯抽采钻孔围岩塑性区内煤体会产生大量裂隙，增大了瓦斯的渗透率，形成瓦斯增透圈，增透圈半径的大小直接影响瓦斯的抽采效果。以钻孔围岩“蝶形塑性区”理论为基础，建立了钻孔塑性区与瓦斯增透圈模型，首次推导出了钻孔增透圈半径解析式。深入分析了钻孔增透半径影响因素发现：增透半径与钻孔半径成线性正比例关系，与最小围压和围压比值呈类指数增长关系，与岩石黏聚力和内摩擦角呈负指数变化关系；其中最小围压与围压比值是影响增透半径的关键因素，深部开采与高围压比值是形成大尺寸有效增透圈的必要和充分条件。这一理论为煤与瓦斯共采中瓦斯抽采钻孔间距设计、位置选择、方向确定、采场与钻孔布置在时间和空间上关系协调提供了科学依据。

关键词:煤与瓦斯共采；增透半径；钻孔增透圈；蝶形塑性区；围压比值；深部开采

我国煤层瓦斯赋存丰富，实现矿井煤与瓦斯2种能源共采是现今提倡的绿色开采理念核心之一[1]。钻孔抽采是当前煤与瓦斯共采中瓦斯抽采的主要工程手段，钻孔塑性区对优质瓦斯通道的形成具有重要作用[2]。

为了增大煤层透气性以提高钻孔的抽采效率，学者对煤层注水、水力割缝和水力压裂等各种增透措施做了大量的研究工作[3-8]。然而，由于在浅部、非采动影响条件下钻孔围岩形成的塑性区范围很小对瓦斯的增透效应微乎其微，所以钻孔围岩塑性区的瓦斯增透作用常常被忽视。文献[9-15]在研究圆形巷道围岩塑性区时发现在非等压条件下巷道围岩会产生“蝶形塑性区”，且随着双向压力差值的增大“蝶叶”尺寸成倍增加。文献[2]首次将巷道“蝶形塑性区”理论应用于瓦斯抽采钻孔中，指出在高压力差值条件下钻孔围岩会形成几十倍孔径大小的“蝶形塑性区”，扩大了钻孔的联通范围，形成优质瓦斯通道。目前的理论多采用文献[11]推导出的塑性区边界方程来确定钻孔塑性区的影响范围，方程复杂且为隐式，使用不便。本文建立了钻孔塑性区与瓦斯增透圈的理论模型，推导出了钻孔增透半径的解析式，并对其影响因素进行了理论分析，为煤与瓦斯共采中钻孔的布置提供了理论依据。

1钻孔塑性区与瓦斯增透圈理论模型

在矿山压力作用下，位于煤体中的瓦斯抽采钻孔周围将出现一定范围的塑性区，塑性区内的煤体产生大量裂隙，导致瓦斯渗透率增加，形成钻孔瓦斯增透区域。为了表征钻孔对瓦斯增透范围的大小，定义塑性区最大边界对应的外接圆为瓦斯增透圈。图1为钻孔塑性区与瓦斯增透圈理论模型示意。

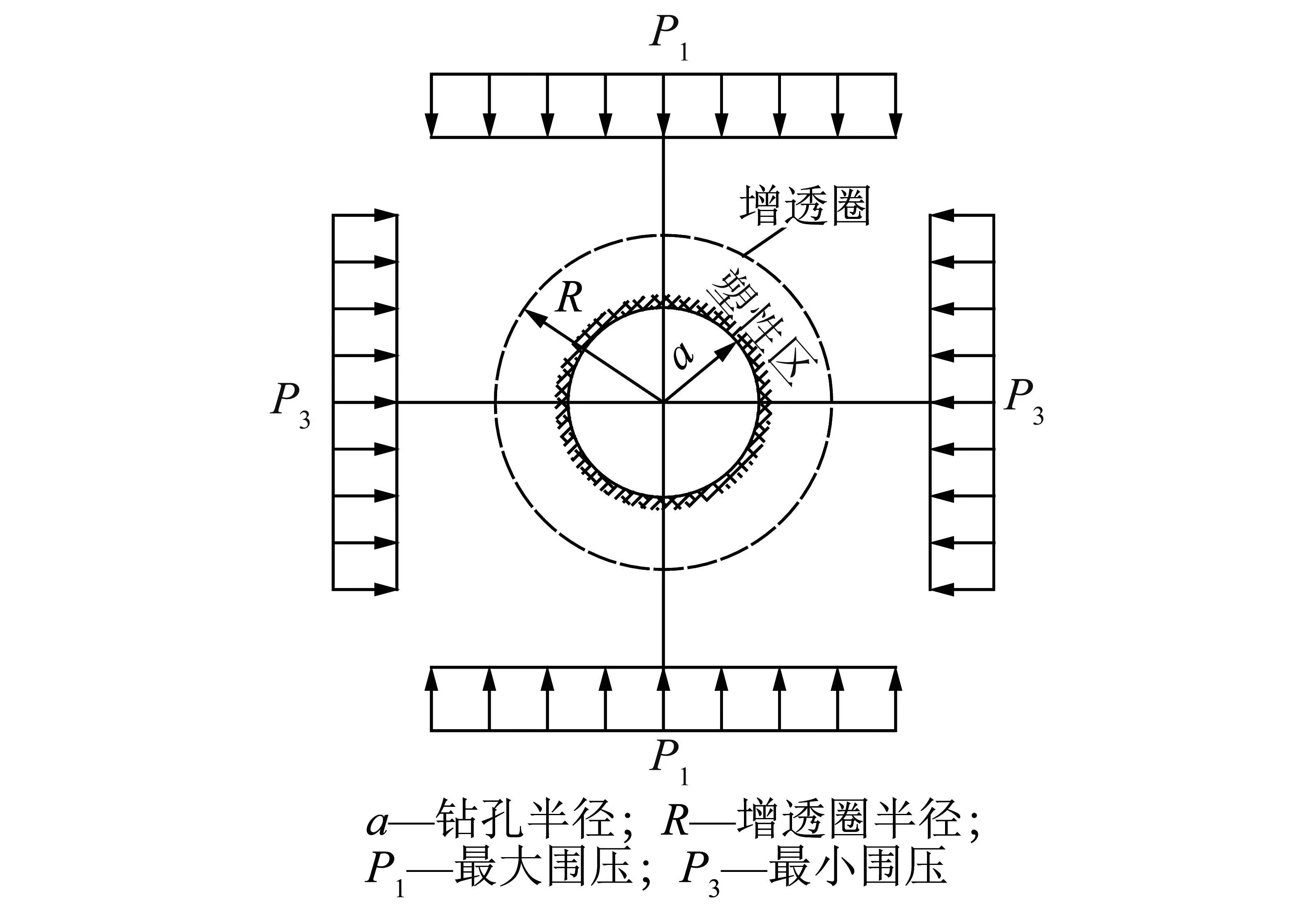
图1　钻孔塑性区与瓦斯增透圈理论模型Fig.1　Theoretical model of the drilling plastic zone and gas permeability-increasing circle

文献[11]推导出了非均匀应力场中钻孔围岩塑性区边界隐性方程：

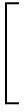
(1)

式中,r,θ为塑性区边界任一点的极坐标；C为岩石黏聚力；φ为岩石内摩擦角；η为围压比值，η=P1/P3。

式(1)结果表明，在围岩岩性一定的条件下，钻孔双向围压比值决定了钻孔围岩塑性区的形态及范围大小：当η=1时，图1为双向等压受力模型，钻孔围岩塑性区为圆形；随着η的增大，钻孔围岩将形成蝶形塑性区，且蝶叶尺寸不断扩大，当η增大到一定值时蝶叶最大尺寸将达到钻孔半径的几十倍。图2为岩石岩性一定(P1=20 MPa，a=0.05 m，C=5 MPa，φ=29°)时，在不同围压比值条件下钻孔塑性区与瓦斯增透圈理论计算图，可以发现当钻孔所处围压比值较小时，钻孔增透圈非常小，半径甚至不足0.1 m；随着η的增大，增透圈也不断增大，当η增大到18时，增透圈半径达到1.08 m，为钻孔半径的21倍。

钻孔增透圈半径(简称增透半径)的大小直接影响钻孔瓦斯抽采的效果，增透半径越大瓦斯抽采效果越好。

2钻孔增透半径解析解的理论分析

2.1塑性区蝶叶最大半径对应极角特征

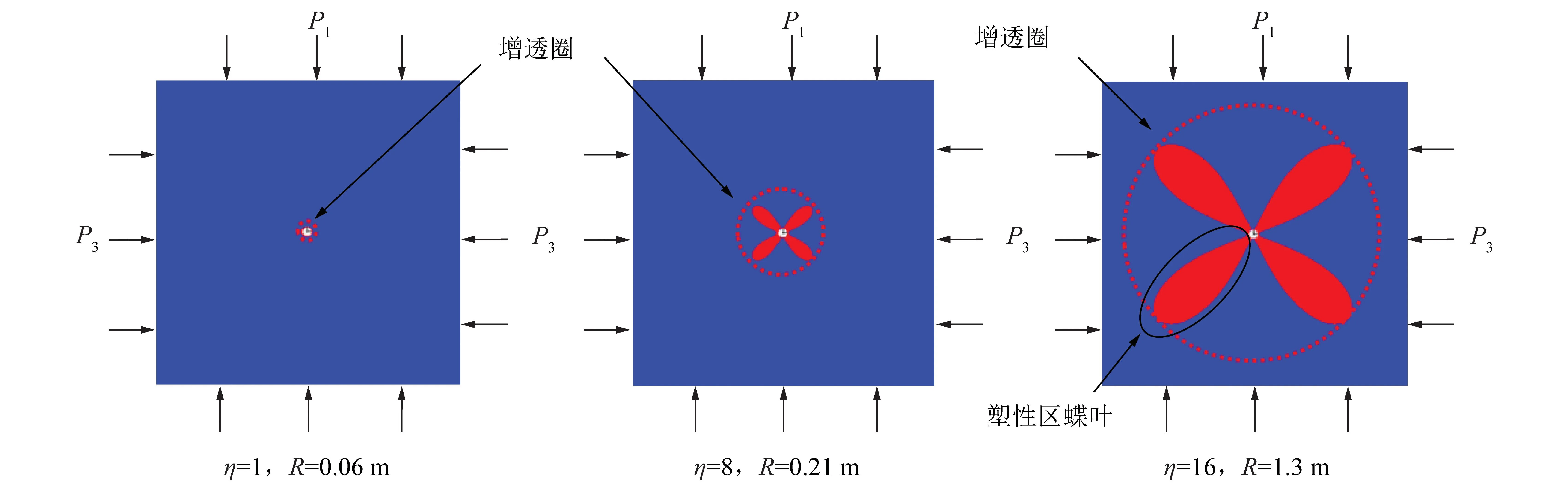
图2　不同围压比值下钻孔塑性区与瓦斯增透圈Fig.2　Drilling plastic zone and gas permeability-increasing circle in different confining pressure ratio

图3　蝶叶最大半径对应极角θ与蝶叶最大半径关系Fig.3　Relationship between butterfly leaf’s maximum radius corresponding polar angle and maximum radius

根据边界方程可求出一定条件下钻孔围岩塑性区边界范围。图3为3种岩石强度条件下蝶叶最大半径对应极角θ与蝶叶最大半径关系图(均质条件下蝶形塑性区具有对称性，所以只研究第1象限内蝶叶情况)。研究发现，在一定围压条件下钻孔围岩出现蝶形塑性区后，不管蝶叶尺寸如何变化第一象限蝶叶最大半径对应极角基本在45°附近。岩石强度较低时，如图3(a)所示，η=6塑性区开始出现蝶叶，蝶叶最大半径约为孔径的2.3倍，对应极角θ为44.2°，随着η的增大蝶叶半径不断增大，最大半径对应极角θ也在增大，η=8.5时蝶叶最大半径约为孔径25倍，对应极角θ为45.7°。在中等岩石强度条件下，如图3(b)所示，从开始出现蝶叶到蝶叶最大半径为孔径23倍，蝶叶最大半径对应极角θ从44.5°变为45.5°，θ偏离45°最大不超过0.5°。岩石强度较高时，如图3(c)所示，蝶叶最大半径对应极角θ接近45°程度更高，偏离值最大不超过0.4°。可见，钻孔围岩出现蝶形塑性区后，蝶叶最大半径对应极角在45°附近。

2.2钻孔增透半径解析式

上文分析得到，钻孔围岩出现蝶形塑性区后蝶叶最大半径对应极角都稳定值在45°附近，最大偏差值不超过1°，可把45°处塑性区边界半径作为钻孔的增透半径。把θ=45°代入塑性区边界方程(1)得到关于增透半径的方程式：

(2)

式(2)是关于a/R的一元八次方程，其中八次、六次、二次项系数均为(1-η)2的整数倍，方程提出公因式变形得到

(3)

(4)

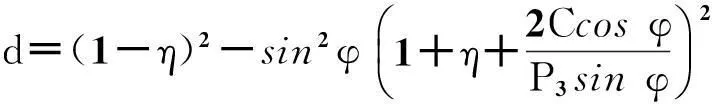
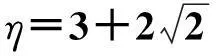
(5)

(2)当b≠0时方程(4)是关于X的一元二次方程，解方程得

(6)

X2=-c-c2-4bd2b(7)

(8)

把各参数代入公式(5)和(8)得到瓦斯抽采钻孔增透半径的解析式：

(9)

2.3增透半径解析式误差分析

2.3在求解增透半径解析式过程中把45°边界半径作为蝶叶边界最大半径且在解方程过程中省去微小项，所以所求增透半径解析式与准确值存在偏差。

表1为在3种不同岩石强度条件下，通过计算机计算式(1)得到蝶叶最大半径Rmax和在相同条件下通过解析式得到的增透半径R对比表。由表1可以看出，解析式所求的增透半径值与准确值相比偏小但非常接近，相对误差最大不超过3%，绝对误差最大不超过钻孔半径的1倍，钻孔半径一般为50 mm左右，所以绝对误差最大的都不超过50 mm。图4是蝶叶最大半径为孔径20倍左右时，在3种不同岩性条件下式(1)所求蝶叶最大半径与解析式求得增透半径对比图，从图4可更直观看出解析式增透半径与式(1)蝶叶最大半径高度吻合。

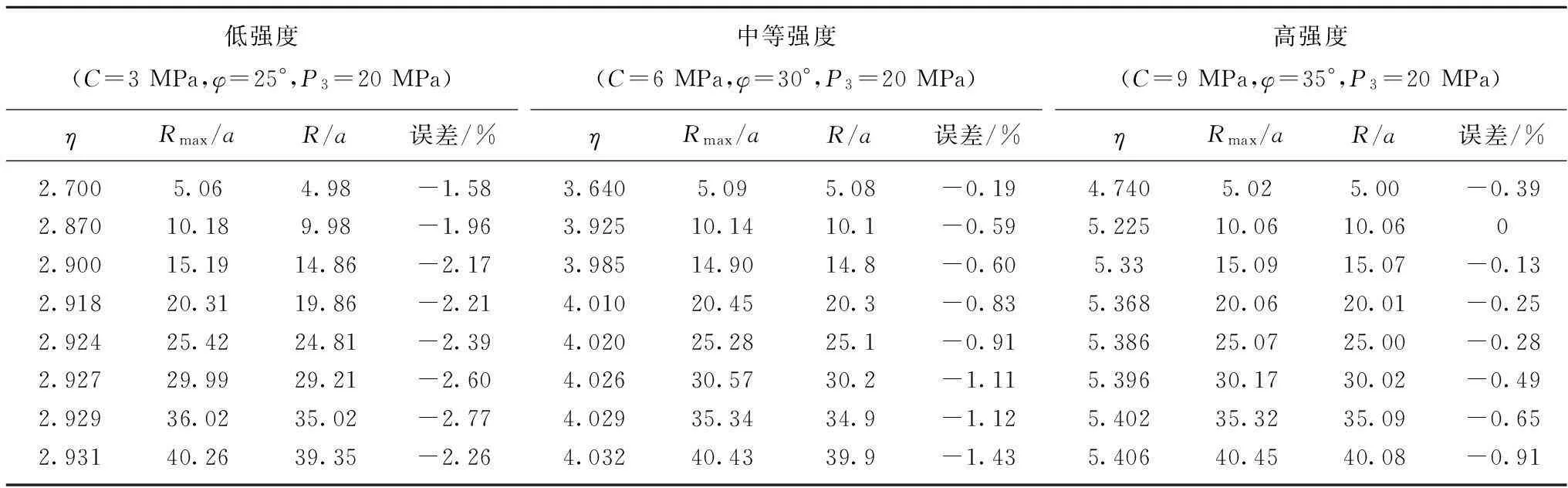
表1　3种岩石强度条件下蝶叶最大半径和解析式半径对比

3钻孔增透半径的影响因素

由钻孔增透半径表达式(9)可以看出，影响钻孔增透半径的因素有钻孔半径、围压比值、最小围压值、岩石黏聚力、岩石内摩擦角，下面将详细分析各因素对钻孔增透半径的影响。

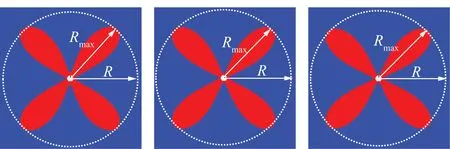
图4　蝶叶最大半径与解析式半径对比Fig.4　Comparison between the butterfly leaf’s maximum radius and the radius of analytic formula

(1)钻孔半径。

控制其他因素不变，钻孔半径从0.05～0.20 m以0.01 m间隔变化时，研究3种不同岩石强度的钻孔增透半径的变化趋势，如图5所示。由图5可以得出，钻孔增透半径与钻孔半径成线性正相关关系，即随着钻孔半径的增大，增透半径线性增大，此性质从增透半径表达式也可以看出。增透半径与钻孔半径线性关系的直线斜率由岩石岩性决定，当岩石强度较低时直线斜率较大；在相同条件下，低强度岩石的钻孔增透半径大于高强度。在条件允许范围内，应尽量增大钻孔孔径以扩大增透半径，提高瓦斯抽采效率。

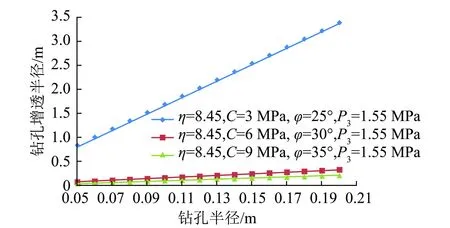
图5　钻孔增透半径与钻孔半径关系Fig.5　Relationship between permeability-increasing radius and radius of the hole

(2)围压比值。

钻孔所受围压比值是影响增透半径的重要因素，图6为3种不同岩石强度的钻孔增透半径与围压比值关系图。由于岩石强度较大时破坏需要更大围压，为了在有限的围压比值范围内得到完整的曲线图，在研究时强度大的岩石适当增大了其所受的最小围压值。由图可得，围压比值较小时3种强度岩石的增透半径都很小且数值相近，基本为钻孔半径，围压比值的变化对钻孔增透半径影响不明显；当围压比值达到一定值后，如图6所示，低强度的曲线在围压比值达到7，高强度的需要在围压比值达到16以后，增透半径随围压比值迅速增长，可达到钻孔半径的十几倍甚至几十倍；不同的岩石强度钻孔增透半径与围岩比值关系曲线具有相似的变化趋势，只是岩石强度较大时，出现较大增透半径需要更大的围压比值。

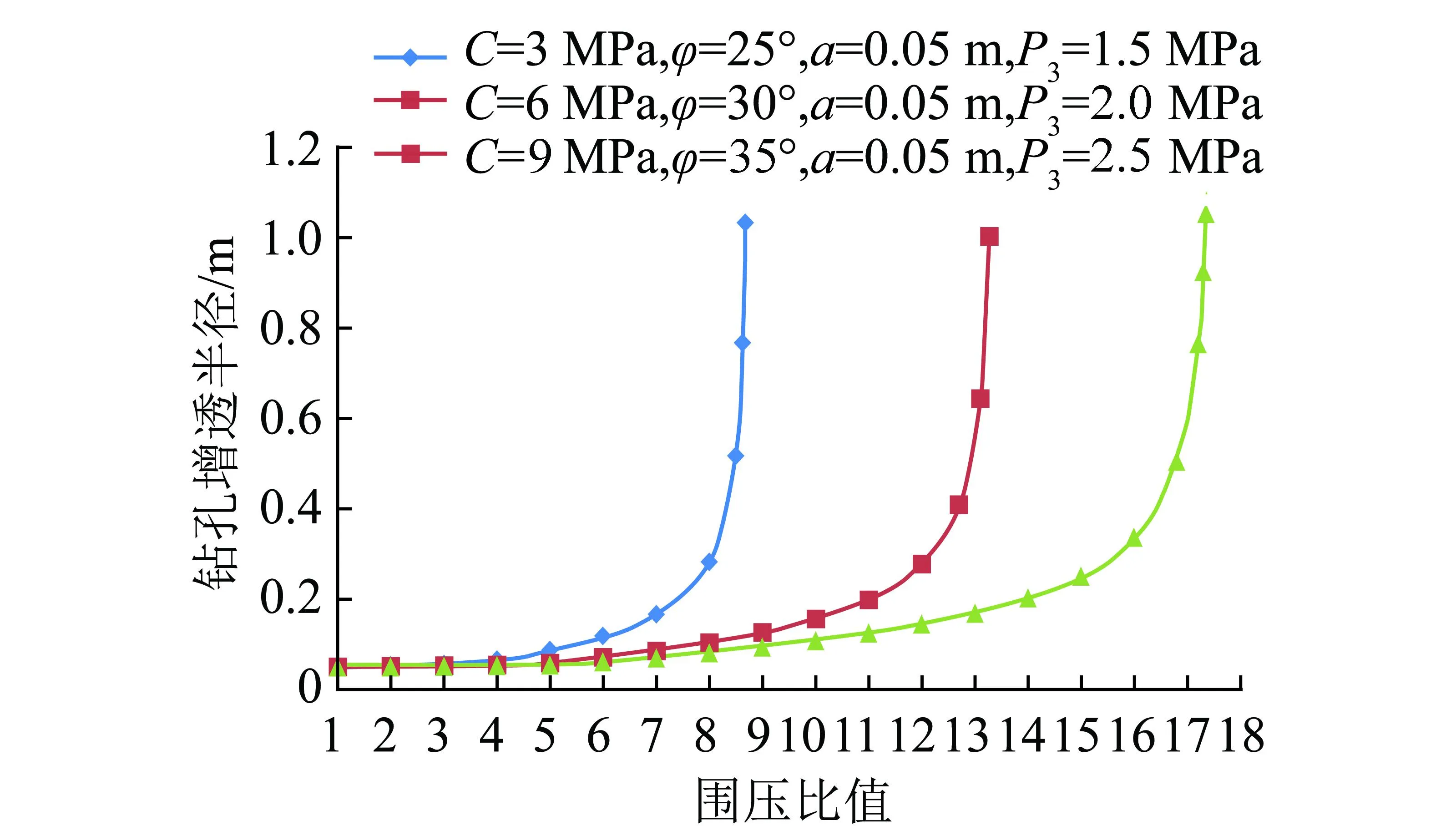
图6　钻孔增透半径与围压比值关系Fig.6　Relationship between permeability-increasing radius and confining pressure ratio

(3)岩石黏聚力。

岩石的黏聚力是影响岩石强度的重要参数，图7为钻孔增透半径与岩石黏聚力的关系。随着岩石黏聚力的增加钻孔增透半径逐渐减小，黏聚力无限增大时增透半径变化趋于平缓逐渐接近钻孔半径，钻孔的增透作用几乎为零。随着岩石黏聚力的增大岩石强度在增大，钻孔围岩形成的塑性区逐渐减小，钻孔增透半径会不断减小，当黏聚力增大到一定值后，钻孔失去增透作用，对于抽采瓦斯不利。图7中3条曲线对比再次证明低强度高围压比值更容易形成大的增透半径。

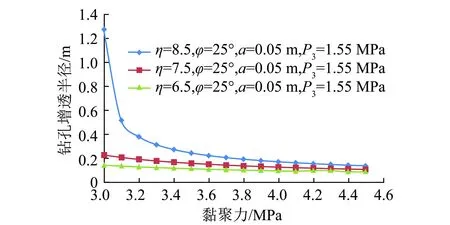
图7　钻孔增透半径与岩石黏聚力关系Fig.7　Relationship between permeability-increasing radius and the cohesion

(4)岩石内摩擦角。

与岩石黏聚力相似，岩石内摩擦角是影响岩石强度的另一个重要参数，图8为钻孔增透半径与岩石内摩擦角的关系图。由图8可得，随着岩石内摩擦角的增加钻孔增透半径逐渐减小，内摩擦角增大到一定值后继续增大时增透半径变化趋于平缓逐渐接近钻孔半径，钻孔的增透作用几乎为零，此时对于抽采瓦斯不利。岩石内摩擦角较小时，随着内摩擦角减小钻孔增透半径迅速增长，如图8中蓝色曲线内摩擦角为25°时钻孔增透半径达到1.27 m，约为钻孔半径的25倍，此时对于抽采瓦斯有利。

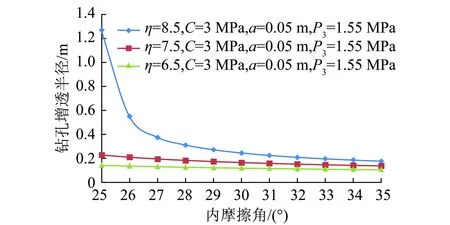
图8　钻孔增透半径与岩石内摩擦角关系Fig.8　Relationship between permeability-increasing radius and the internal friction angle

(5)最小围压与开采深度。

钻孔围压与钻孔布置深度有关，一般地质条件下原岩应力场中水平应力大于垂直应力，在钻孔塑性区与瓦斯增透圈理论模型中可将垂直应力作为最小围压值，其大小为上覆岩层的自重应力，即P3=γH，γ为上覆岩层平均容重，H为开采深度，随着埋深的增加，最小围压线性增大。图9为不同岩石强度条件下钻孔增透半径随开采深度的变化关系。由图9可得，3条曲线具有相似的变化趋势：开采深度较浅时，随着深度的增加增透半径缓慢增大，当深度达到一定值后随着深度继续增加增透半径迅速增大，甚至可达到钻孔半径的几十倍大小。岩石强度较大时，出现较大增透圈需要更大的围压值，钻孔就要求布置在更深位置。

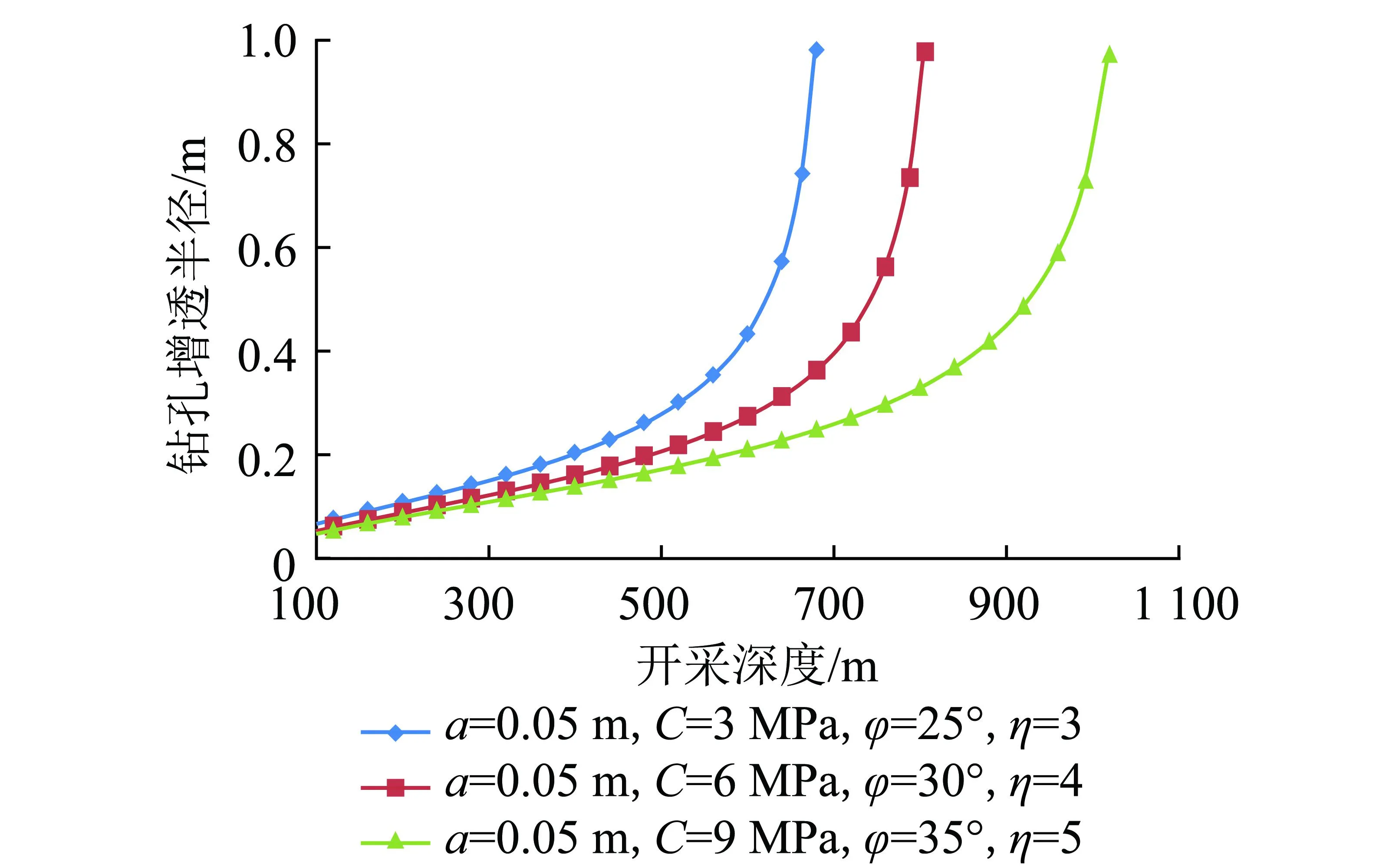
图9　钻孔增透半径与开采深度关系Fig.9　Relationship between permeability-increasing radius and the depth of drilling

钻孔增透半径的大小与5个因素相关，但5个影响因素有主次之分。增透半径与钻孔半径成线性正比例关系，但比例系数却至关重要，当比列系数较小时单纯依靠扩大孔径来增大增透圈半径作用有限，所以钻孔半径为次要影响因素；在实际地质条件下，岩层和岩石强度已经客观存在，岩石的黏聚力和内摩擦角为非人为可控因素；在采矿工程活动中会形成“加载”和“卸荷”效应从而改变钻孔围压比值，且只有在达到一定的开采深度后才会有足够破坏围岩形成增透圈的围压力，所以围压比值和开采深度是影响增透半径的关键因素。通过上文对钻孔增透半径影响因素分析可知，只有当开采深度和围压比值增大到一定值后才会形成大的增透圈，所以深部开采与高围压比值是形成大尺寸有效钻孔增透圈的必要和充分条件。

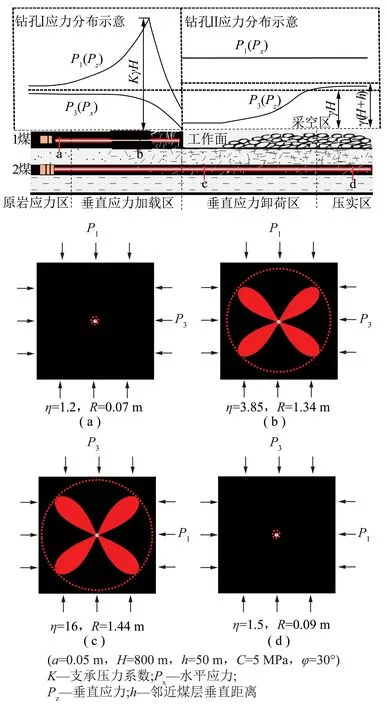
图10　采场附近应力分布、分区及对应钻孔增透圈Fig.10　Stress distribution and partition near the stope and corresponding drilling permeability-increasing circle

4增透圈在煤与瓦斯共采中的应用

上文研究表明，瓦斯抽采钻孔在深部、高围压比值条件下围岩将产生有利于瓦斯抽采的增透圈，在钻孔深度和围压比值达到一定值后增透半径随着围压比值的增加而迅速增长，在钻孔周围形成范围较大的瓦斯增透区域，提高了瓦斯抽采效果。

采矿工程活动引起的“加载”与“卸荷”效应形成了高围压比值环境，为钻孔增透圈形成创造有利条件，图10为采场附近应力分布、分区及对应钻孔增透圈示意图。

在工作面前方，水平应力由零逐渐增大趋近于原岩应力，垂直应力先增大至最大值后逐渐减小趋近于原岩应力，形成“垂直应力加载区”(简称“加载区”)；在工作面后采空区下方，由于煤体开采的“卸荷”作用使下邻近层煤体所受垂直应力锐减，随着采空区顶板垮落压实垂直应力逐渐恢复至原岩应力，水平应力基本不变，在工作面后采空区下方形成“垂直应力卸荷区”(简称“卸荷区”)。“加载区”钻孔所受最大围压为垂直应力最小围压为水平应力，围压比值近似等于工作面前方支承压力系数，在图10所示条件下钻孔增透半径为1.34 m，约为钻孔半径的27倍；“卸荷区”钻孔所受最大围压为水平应力最小围压为垂直应力，围压比值最大可达到16以上[2]，在图示条件下钻孔增透半径为1.44 m,约为钻孔半径的29倍。

抽采本开采煤层瓦斯时，钻孔应垂直工作面水平布置，如图10中钻孔Ⅰ。钻孔通过工作面前方的“加载区”，围压比值可近似等于工作面前方支撑压力系数，在高围压比值环境下形成有利于瓦斯抽采的增透圈，随着工作面向前推进，“加载区”同时向前推移，钻孔在“加载区”部分一直处在高围压比值环境中，瓦斯增透圈大，可持续高效抽采瓦斯。

预抽采“卸荷”下邻近层瓦斯时，应在上工作面回采之前在下邻近煤层中预先布置水平钻孔，如图10中钻孔Ⅱ。如果上工作面回采后再布置钻孔，采空区后方压实垂直应力恢复，高围压比值环境消失，钻孔周围不会形成有利于瓦斯抽采的增透圈。图11通过计算机数值模拟方法得到了采深800 m、长200 m工作面下方围岩主应力比值云图，可以看出采空区下方“卸荷区”不同层位形成稳定的高围压比值环境。在高围压比值带内钻孔所受最大围压为水平应力，近似等于上覆岩层自重应力，即P1=γH，钻孔所受最小围压P3=P1/η，据此可计算出不同围压比值带内钻孔增透圈。由图11可得，采空区下方“卸荷区”不同层位形成了不同的围压比值带，Ⅱ层位围压比值最高可达到16.6，对应钻孔增透半径为1.3 m约为孔径的26倍，钻孔布置在这一区域可提高瓦斯的抽采效率。

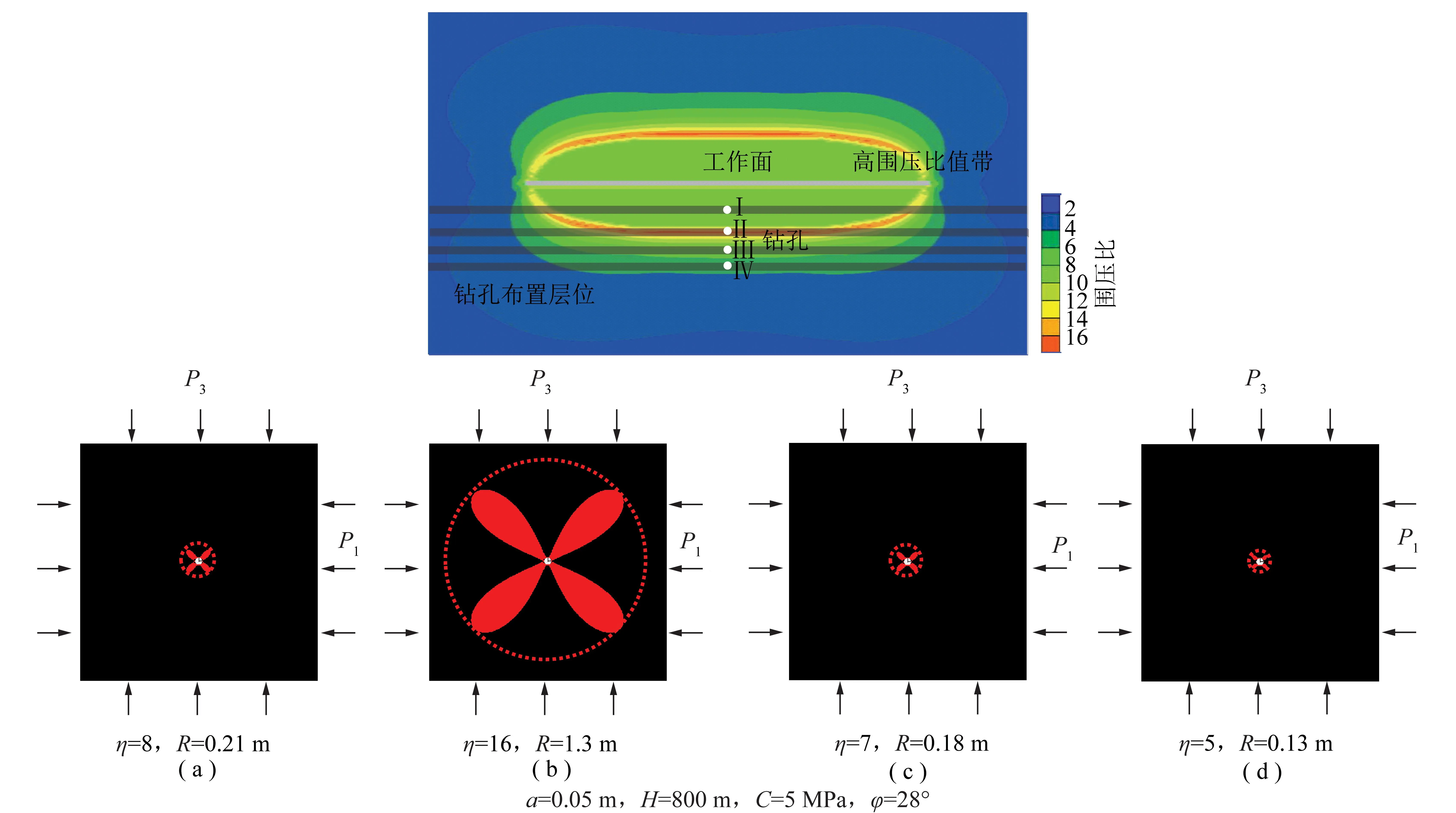
图11　卸荷区高围压比值带与带内钻孔增透圈Fig.11　High confining pressure ratio belt in unloading zone and drilling permeability-increasing circle

5结论

(1)建立了钻孔塑性区与瓦斯增透圈的理论模型，推导出了钻孔增透半径解析式，可以作为瓦斯抽采钻孔间距设计、位置选择、方向确定、采场与钻孔布置在时间和空间上关系协调的理论计算基础。

(2)增透半径与钻孔半径呈线性正比列关系，与最小围压和围压比值呈类指数增长关系，与岩石黏聚力和内摩擦角呈负指数变化关系。

(3)最小围压与围压比值是影响增透半径的关键因素，深部开采与高围压比值是形成钻孔较大增透圈的必要和充分条件。

(4)采矿工程活动引起的“加载”与“卸荷”效应形成了高围压比值带，将钻孔布置在这些高围压比值区域将形成大的钻孔增透圈，有利于瓦斯抽采。

参考文献：

[1]缪协兴，钱鸣高.中国煤炭资源绿色开采研究现状与展望[J].采矿与安全工程学报，2009,26(1):1-14.

Miao Xiexing,Qian Minggao.Research on green mining of coal resources in China:Current status and future prospects[J].Journal of Mining & Safety Engineering,2009,26(1):1-14.

[2]马念杰，李季，赵希栋，等.深部煤与瓦斯共采中的优质瓦斯通道及其构建方法[J].煤炭学报，2015,40(4):742-748.

Ma Nianjie,Li Ji,Zhao Xidong,et al.High quality gas channel and itsconstruction method applied to coal and gasin deep mining[J].Journal of China Coal Society,2015,40(4):742-748.

[3]杨天鸿，于庆磊，王善勇，等.荷载和水压力作用下岩石裂纹贯通过程的数值模拟研究[J].岩石力学与工程学报，2005,24(1):5026-5030.

Yang Tianhong,Yu Qinglei,Wang Shanyong,et al.Study on crackcoalscence process under loading and hydraulic pressure[J].Chinese Journal of Rock Mechanics and Engineering,2005,24(1):5026-5030.

[4]林柏泉，张其智，沈春明，等.钻孔割缝网络化增透机制及其在底板穿层钻孔瓦斯抽采中的应用[J].煤炭学报，2012,37(9):1425-1430.

Lin Baiquan,Zhang Qizhi,Shen Chunming,et al.Permeability-increasing mechanism of network slotting boreholes and application in crossing borehole gas drainage[J].Journal of China Coal Society,2012,37(9):1425-1430.

[5]穆朝民，王海露.煤体在高压水射流作用下的损伤机制[J].岩土力学，2013,34(5):1515-1520.

Mu Chaomin,Wang Hailu.Damage mechanism of coal under high pressure water jetting[J].Rock and Soil Mechanics,2013,34(5):1515-1520.

[6]杨永明，鞠杨，陈佳亮，等.三轴应力下致密砂岩的裂纹发育特征与能量机制[J].岩石力学与工程学报，2014,33(4):691-698.

Yang Yongming,Ju Yang,Chen Jialiang,et al.Cracks development features and energy mechanism of dense sandstone subjected to triaxial stress[J].Chinese Journal of Rock Mechanics and Engineering,2014,33(4):691-698.

[7]闫发志，朱传杰，郭畅，等.割缝与压裂协同增透技术参数数值模拟与试验[J].煤炭学报，2015,40(4):823-829.

Yan Fazhi,Zhu Chuanjie,Guo Chang,et al.Numerical simulation parameters and test of cutting and fracturing collaboration permeability-increasing technology[J].Journal of China Coal Society,2015,40(4):823-829.

[8]翟成，李贤忠，李全贵.煤层脉动水力压裂卸压增透技术研究与应用[J].煤炭学报，2011,36(12):1996-2001.

Zhai Cheng,Li Xianzhong,Li Quangui.Research and application of coal seam pulse hydraulic fracturing technology[J].Journal of China Coal Society,2011,36(12):1996-2001.

[9]林远东，涂敏.非均应力场圆形巷道围岩塑性区解析分析[J].煤炭科技，2011(2)：27-28.

Lin Yuandong,Tu Min.Analytical analysis of non-uniform force field circular surrounding rock plastic zone[J].Coal Science and Technology,2011(2):27-28.

[10]陈立伟，彭建兵，范文，等.基于统一强度理论的非均匀应力场圆形巷道围岩塑性区分析[J].煤炭学报，2007,32(1)：20-23.

Chen Liwei,Peng Jianbing,Fan Wen,et al.Analysis based on unified strength theory of non-uniform stress field circular roadway for plastic zone[J].Journal of China Coal Society,2007,32(1):20-23.

[11]赵志强.大变形回采巷道围岩变形破坏机理与控制方法研究[D].北京：中国矿业大学(北京)，2014.

Zhao Zhiqiang.Mechanism of surrounding rock deformation and failure and control method research in large deformation mining roadway[D].Beijing:China University of Mining & Technology(Beijing),2014.

[12]刘朝科，任建喜.非均匀应力场圆形巷道塑性区研究[J].煤矿安全，2014,43(3):42-45.

Liu Chaoke,Ren Jianxi.Study on plastic zone of circular roadway under non-uniform stress field[J].Safety in Coal Mines,2014,43(3):42-45.

[13]马念杰，李季，赵志强.圆形巷道围岩偏应力场及塑性区分布规律研究[J].中国矿业大学学报，2015,44(2):206-213.

Ma Nianjie,Li Ji,Zhao Zhiqiang.Distribution of the deviatoric stress field and plastic zone in circular roadway surrounding rock[J].Journal of China University of Mining & Technology,2015,44(2):206-213.

[14]张小波，赵光明，孟祥瑞.基于岩石非线性统一强度准则的非均匀应力场中圆形巷道围岩塑性区分析[J].安全与环境学报，2013,13(3):202-206.

Zhang Xiaobo,Zhao Guangming,Meng Xiangrui.Plastic zone analysis of the surrounding rock mass in circular tunnel under non-uniform stress field[J].Journal of Safety and Environment,2013,13(3):202-206.

[15]蒋斌松，杨乐，龙景奎.基于对数应变的圆形巷道围岩开挖应力分析[J].中国矿业大学学报，2012,41(5)：707-710.

Jiang Binsong，Yang Le，Long Jingkui.Stress analysis of rock surrounding circular openings:The caving problem and logarithmic strain[J].Journal of China University of Mining & Technology,2012,41(5):707-710.

Theoretical analysis and application about permeability-increasing radius of drilling for simultaneous exploitation of coal and gas

MA Nian-jie，GUO Xiao-fei，ZHAO Xi-dong，LI Ji，YAN Zhen-xiong

(FacultyofResourceandSafetyEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)

Abstract:Under the influence of mining induced loading and unloading stress in simultaneous exploitation of coal and gas,a large number of cracks are generated in the surrounding rock plastic zone of gas drilling,which increases the permeability of gas and forms the permeability-increasing circle whose radius directly affects the effect of gas extraction.Based on the theory of the “butterfly plastic zone”,the model of the borehole plastic zone and the gas permeability-increasing circle was established,and the analytic formula of permeability-increasing circle radius was deduced.The further research on the factors affecting the permeability-increasing radiusreveals that the permeability-increasing radius is linearly positive to the radius of borehole,similarly exponentially positive to the minimum confining pressure and confining pressure ratio,and exponentially negative to the cohesion and the internal friction angle.The minimum confining pressure and confining pressure ratio are the key factors,and the deep mining and high confining pressure ratio are the sufficient and necessary conditions for the formation of effective permeability-increasing circle.This theory provides ascientific basis for the drilling spacing design,location selection,direction determination and the coordination of time and space between mining field and borehole layout.

Key words:exploitation of coal and gas;permeability-increasing radius;permeability-increasing circle of drilling;butterfly plastic zone;confining pressure ratio;deep mining

中图分类号:TD712

文献标志码:A

文章编号:0253-9993(2016)01-0120-08

作者简介:马念杰(1959—)，男，辽宁开原人，教授，博士生导师。E-mail:njma5959@126.com

基金项目:国家重点基础研究发展计划(973)资助项目(2011CB201204)；国家自然科学基金重点资助项目(51234005，51434006)

收稿日期:2015-07-08修回日期:2015-10-10责任编辑:常琛

马念杰，郭晓菲，赵希栋，等.煤与瓦斯共采钻孔增透半径理论分析与应用[J].煤炭学报,2016,41(1):120-127.doi:10.13225/j.cnki.jccs.2015.8005

Ma Nianjie，Guo Xiaofei，Zhao Xidong，et al.Theoretical analysis and application about permeability-increasing radius of drilling for simultaneous exploitation of coal and gas[J].Journal of China Coal Society,2016,41(1):120-127.doi:10.13225/j.cnki.jccs.2015.8005