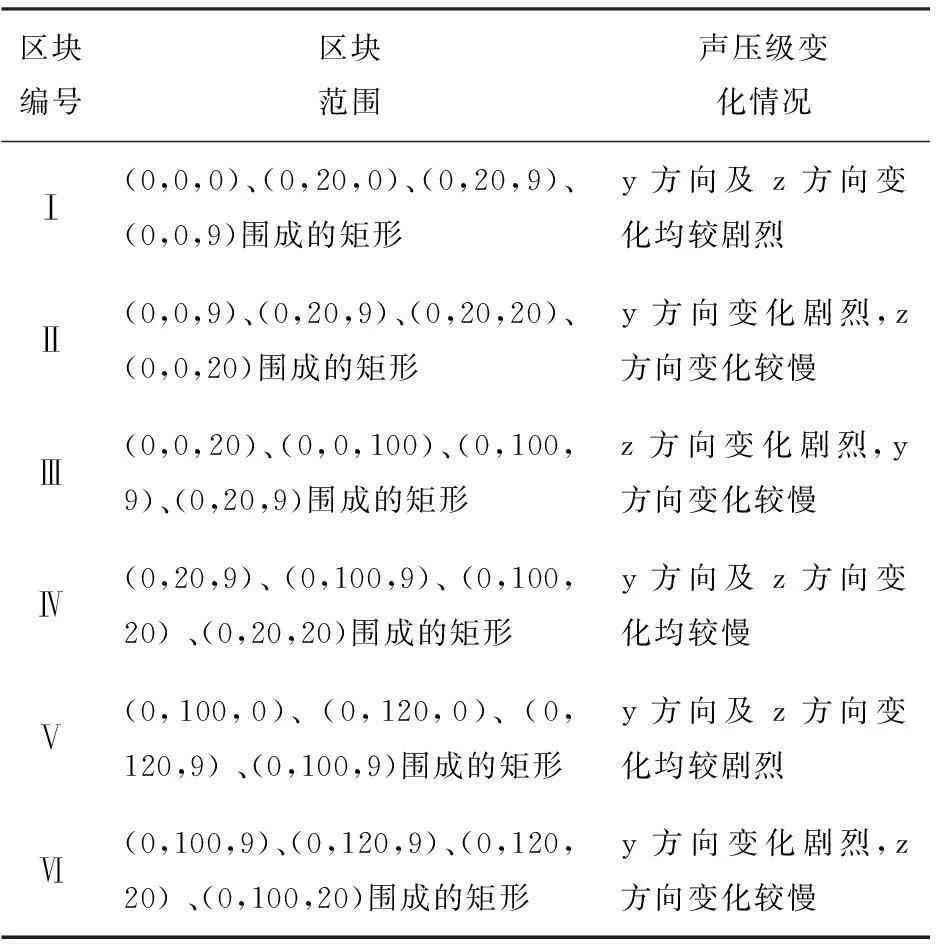
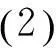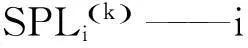围蔽街道噪声测量布点优化研究

周丽君，方廷勇，陈丛波

(安徽建筑大学 土木工程学院,安徽 合肥 230601)



围蔽街道噪声测量布点优化研究

周丽君，方廷勇，陈丛波

(安徽建筑大学 土木工程学院,安徽 合肥 230601)

摘要：围蔽街道噪声测点优化布置的问题对提高噪声测点效率有着重要影响。本文基于遗传算法并运用噪声分析软件，建立了一种噪声测点布置的优化模型。该模型从大量噪声测点中搜索出测点数目最少且与原测点偏离较少的优化测点。然后将该优化模型应用于某一特定围蔽街道，搜索出该街道的最优测点布置方式。结果显示该模型在不影响精度的情况下可减少噪声测点数目，为今后街道噪声测量提供理论依据。

关键词：围蔽街道，测点，优化模型，遗传算法

0引言

目前，我国噪声监测布点普遍采用网格布点的方法，该方法存在测点多、工作量大、监测周期长等诸多不利因素，因此，噪声监测布点优化具有重要意义[1-2]。

本研究基于变网格布点法[3-5]将围蔽街道边界面划分为若干网格，选取网格中心处噪声值代表所在网格噪声值。对于网格布点获得的数据的处理，可采用趋势面法、多项式法、积分法和平均值法来获取监测点数据的均值。[6-10]

本研究采取软件模拟方式获得围蔽街道噪声数据。相比于现场实测方式，通过软件模拟获取围蔽街道噪声数据易于实施。本研究应用噪声地图绘图软件 SoundPLAN完成围蔽街道噪声计算。由于 SoundPLAN 是一款应用时间较长并在国内外噪声工程实践中得到多次检验的声学软件，因此，本研究通过该软件得到的数据结果是能够代表围蔽街道噪声分布的真实情况的。

本研究的意义在于：1、论证用有限的代表性测点反映包括无限多测点的整个围蔽街道声场的可行性和正确性；2、有效减少监测点数，大大减少不必要的计算。

1围蔽街道测量布点优化方法

据前文所述，现行的测量布点优化方法因为各自的局限性，对围蔽街道测量布点优化的效果不理想。这些方法多数以数理统计作为理论基础，在选择点位时有很大的随机性，对于高次非线性问题也存在求解复杂的问题。

本研究试图基于 0-1 型整数规划方法解决围蔽街道测量布点优化问题，以使该问题的求解方法客观、高效。在建立围蔽街道测量布点优化的数学模型时，首先通过噪声模拟软件SoundPLAN 可以得到尽可能多的等网格测点数据，这些测点数量大大超过反映围蔽街道声场需要的测点数量。建立数学模型优化的目的是剔除不具有代表性的测点，使优化后的测点数量越少越好，做出规定：若测点 i 具备代表性，则令 i=1，否则 i=0。通过边界条件的设定，应保证优化后的测点能够反映围蔽街道声场。根据噪声测量标准及相关资料，要使优化后测点能够反映围蔽街道声场，优化前任一测点噪声值在优化后绝对误差不超过1dB，相对误差不超过5%。

对某一区域噪声分布用网格测量法进行测量时，通常的做法是将区域划分成若干等面积的网格，取网格中心点的噪声监测数据代表网格面积内的噪声等级。实测中，对网格中心点的测量数据采用10分钟的连续等效声级做算术平均。[5]实际测量过程中，考虑到噪声源分布、待测区域对噪声等级限制以及人口密度等因素不同，可在噪声源复杂、对噪声等级限制严格以及人口密度大的区域划分更密集的网格，更精确地反应该区域的噪声分布；在噪声源单一、待测区域对噪声等级限制较低以及人口密度不大的区域划分较稀疏的网格，减少测量工作负重和计算量。

本次研究中，参考变网格思想，试图将围蔽街道待测区域划分为不同面积的网格。由于不考虑区域噪声等级和人口因素的影响，本研究根据初次布置测点噪声分布变化梯度对围蔽街道进行分区，对每一区域分别设置不同密度的网格，以网格中心作为测点。

本研究建立优化模型本质上属于整数规划问题，目前，求解该类问题的已有方法包括：分枝定界法——可求纯或混合整数线性规划、割平面法——可求纯或混合整数线性规划、隐枚举法——可求解 0-1 整数规划、匈牙利法——解决指派问题、蒙特卡洛法等经典方法。然而，当问题规模扩大时，这些经典方法求解计算量极大，往往无法求解。遗传算法[12-14]来源于自然界的物理过程，与 0-1 整数规划问题结合紧密。该算法属于求解全局最优化问题的随机性方法，对在大搜索空间内寻找最优解有很好效果，能有效解决NP难问题、避免陷入局部最优并对初值没有强依赖关系。

2围蔽街道布点优化实例

2.1围蔽街道声场基本信息

考虑街道两边建筑无间隔的完全围蔽街道， 街道长度L=120m;街道两旁建筑外立面为两临界面,临界面垂直地面设置,临界面间宽度W=20m；街道两旁建筑高度，即围蔽高度H=20m。围蔽街道噪声源来自街道的交通噪声，交通道路所处高度为0，不发生起伏。在噪声模拟软件 SoundPLAN 中导入图中所示围蔽街道声场模型，设置道路 ADT 为 1600Veh/24h，反弹次数为3次，选取昼间噪声作为分析对象，道路噪声情况如表1。

表1　交通声源计算结果

初始布置测点时，考虑应尽可能多布置，以保证初始布置点数满足能够代表围蔽街道声场真实情况。由于本例中围蔽街道两外立面是对称的，具有相同的形状和特性阻抗，并且噪声源位于两边界面中间，因而布点时只需能准确描述出任一边界面声场分布，另一边界面也与此相同。本例中，初始布点将左侧边界面划分边长l=1m的网格,网格连线的交点即为初始测点。初始布点总数N0用公式1计算：

(1)

计算结果显示本例中，初始共布点2400个。设想，如果采用现场实测的方式，花费人力物力成本会大大超出预期，即使采用数值模拟方法，计算量也非常巨大且不必要。取得初始布点噪声数据后，本文试图进一步减少测点数目，优化布点。本例中，在SoundPLAN 中对围蔽街道布置初始测点如图1，保证测点密度使测点处噪声数据能够反映围蔽街道声场性质。对初始测点的噪声数据进行处理，利用 MATLAB 的绘图工具绘制临街边界面的噪声分布图，如图2、图3。现对噪声分布情况进行分析，求得较适合的变网格划分区块。沿街道长度方向，用右侧测点声压级减去同高度的相邻左侧测点声压级并取绝对值，得到沿街道长度方向声压级变化绝对值，由于数据较多，用伪色图的形式表示，如图4。沿边界面高度方向，用高处测点声压级减去同长度的相邻低处测点声压级并减去绝对值，得到沿边界面高度方向声压级变化绝对值，如图5。

图1　围蔽街道初始布置测点分布图示

图2　围蔽街道边界面初始测点声压级变化伪色图

图3　围蔽街道边界面初始测点声压级变化曲面图

图4　初始测点长度方向声压级变化绝对值伪色图

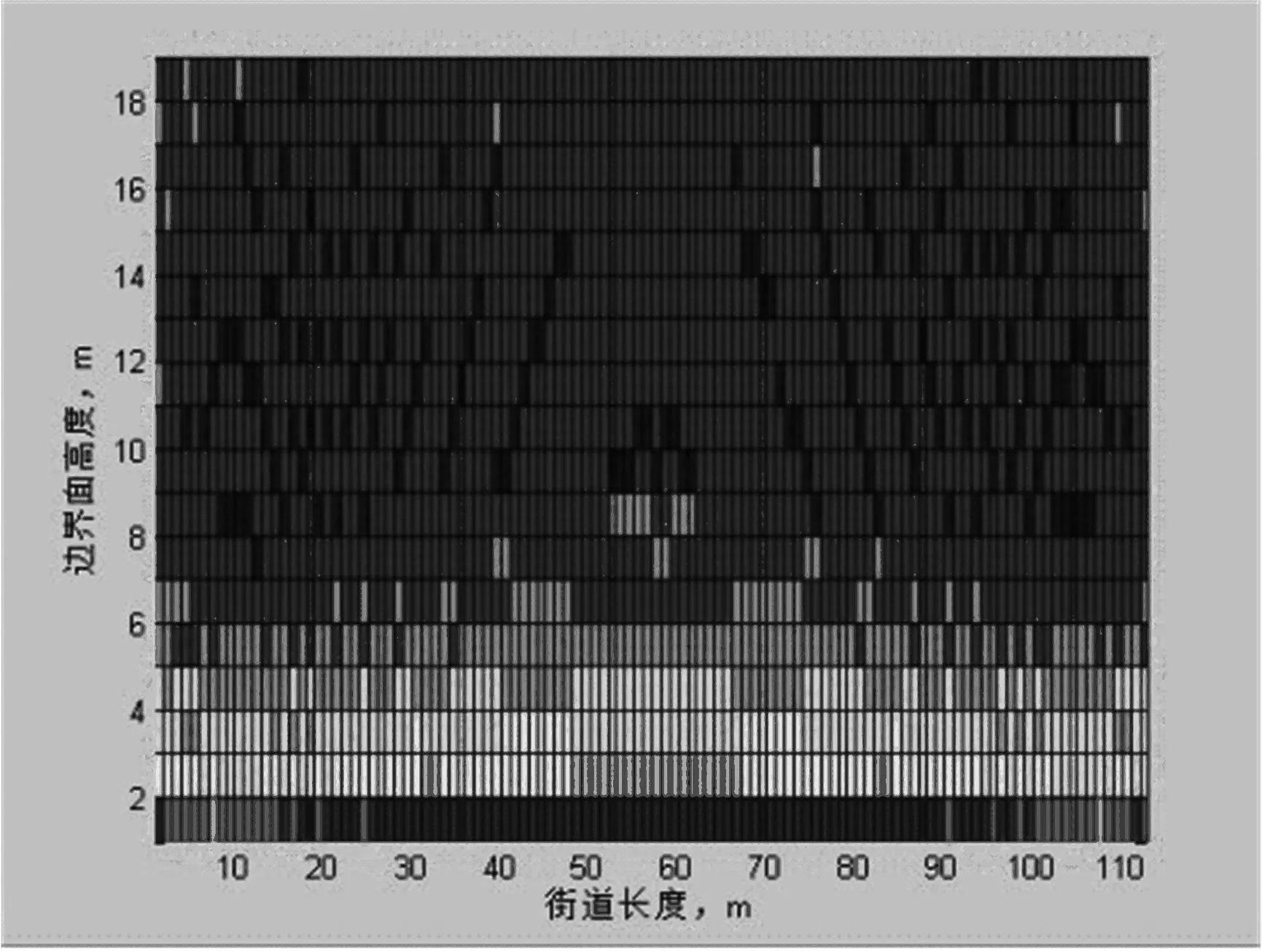
图5　初始测点高度方向声压级变化绝对值伪色图

将围蔽街道宽度方向设为 x 轴，长度方向设为 y 轴，高度方向设为 z 轴，建立直角坐标系，边界面为 x=0 及 x=20 的平面。在 x=0(或 x=20)的平面优化测点前，先根据上述结论对边界面进行分区。将声压级变化剧烈的测点分为一区，设置较密集的测点；将声压级变化较慢的测点分为一区，测点设置可较为稀疏。本例中,将边界面分为6个区块，如表2。

2.2建立模型

为确保优化后测点布置能够代表整个围蔽街道声场，此处借用可观性概念[15]。将可观性定义如下：第 k 次优化后，布点总数Nk

表2　围蔽街道边界面噪声声压级区块划分

规则 1：若点 i 处布置有测点，则点i处声压级可直接预测，故点i具有可观性。

规则 2：点 i 未布置测点，但在点i附近有测点j，测点j 处声压级接近点 i，则可用测点 j 声压级代表点 i 声压级，故点i 具有可观性。

规则 2 中需对“附近”及“接近”做出准确定义。第 k 次优化时，网格边长为l(k)，i、j 点在 x-z 轴平面直角坐标系坐标分别为(xi,zi)和(xj,zj)，若满足

则称点i在点j附近。

设第 k 次优化时，i 点处布置有测点，j 点在 i 点附近，未设置测点，若满足

(3)

则称点 j 处声压级与点 i 处声压级接近。

式2表明 j 点经k次优化后声压级改变的真实值不超过 1dB；式3表明j点经 k 次优化后声压级改变的相对值不超过初始值的 5%。

设第 i 个区块第 j 个测点处噪声声压级为SPLij，Ni为第 i 个区块测点的总数。如前所述，xij=1，xij表示选取第 i 个区块第 j 个测点作为优化后测点；反之，xij=0表示优化后该测点被舍弃。K 表示经 K 次优化后测点布置达到最优。构造测点优化的数学模型如下：

(4)

(5)

(6)

(7)

式中，i=1,2,3,4,5,6;j=1,2,…,Ni。

2.3优化结果及分析

采用遗传算法求解围蔽街道测点分布优化问题，求解得到的测点最优布置方式见图6，需做出说明的是，运用遗传算法得出的布点方式带有一定的随机性，每次运算得出结果未必完全相同，图中所示的布点方式是根据遗传算法得到结果，并通过将测点在满足约束条件情况下修正后得出。依照图中所示布点方式，边界面 6 个区块统计结果如表3。

图6　优化后边界面测点分布图示

3结论

(1)针对围蔽街道测点布置问题，提出从噪声分析软件 SoundPLAN 模拟数据出发，根据噪声声压级变化情况划分区块，在整个围蔽街道区域内进行变网格布点；

(2)在单个区块内，运用遗传算法进行等网格布点。既避免了等网格布点工作量大的问题，也避免了变网格布点计算繁琐的问题；

(3)基于上述布点方法，计算某一特定街道噪声布点问题，结果大大减少了布点数目，并能够反映噪声分布情况。

(4)本文内容解决了有限测点反映围蔽街道区域噪声分布可行性的问题，同时，本文提出的布点方法有望推广于求解其他声环境的实测测点布置问题。

(5)由于影响围蔽街道噪声传播因素众多，实践中难以控制变量，因此通过现场实测方式获取数据验证理论需动用大量人力，反复进行多次实测。本文主要采取软件模拟方式获取数据，尽量保证模拟数据接近真实数据，但模拟数据不能完全准确反映真实围蔽街道的噪声分布。在今后研究中，如有可能，应利用先进声学测量工具，组织大规模有针对性的围蔽街道噪声实际测量，提高数据的准确性。

参考文献

1贺仲雄.模糊数学及其应用[M].天津：天津科学技术出版社 , 1983.

2中国环境科学学会环境质量评价专业委员会.环境质量研究进展[M].贵阳：贵州人民出版社, 276-282, 1985.

3N.E.Huang,Z.Shen,S.R.long,Wu MC,Shih HH,Zheng Q,etal.The Empirical ModeDeeom——osition and The Hilbert SPeetrum for Nonlinear Non-stationary Time Series Analysis[M]. Proc. RoyalSoeiety.London:1998.903-995.

4Zhao Fengqiang,Ma Xiaojiang.Study on the new delivery test method of the noise of transmissions. Proeeedings of the 6th International Conefrenee on Frontiers of Design and Manuafeturing[C]. Xi'an, China, June21-23,2004:629-631.

5赵凤强. 城市环境噪声问题的相关理论方法及应用[D]. 大连：大连理工大学，2006.

6中国科学院地质所.数学地质引论[M].北京:地质出版社，1977.

7张国荣，高虹.用图解趋势分析法计算大气沉降量[J].上海环境科学，1995，14(8)：12-14.

8陈淑媛.多项式方法在大气污染物观测与分析中的应用[J].环境科学研究， 1997，8(4):55-58.

9李婷.锦江河流系统水环境质量评价及污染元素迁移转化模式浅析[D].成都：成都理工大学，2007.

10王艳松,孙桂龙.基于蚁群算法的配电网谐波量测点优化配置[J].中国石油大学学报，2014,1(38)：168-169.

11张全新. 遗传算法--原理及应用[D]. 兰州：兰州铁道学院, 1999.

12李敏强. 遗传算法的基本理论与应用[M].北京：科学出版社, 2002.

13Goldberg D E. Genetic Algorithms in Search, Optimization, and Machine Learning[M]. Addison-Wesley Professional, 1989.

14Michalewicz Z. Genetic Algorithms + Data Structures = Evolution Programs[M]. Springer Berlin Heidelberg, 1992.

15陈妍，刘嘉俊，邱小军. 不同声学边界长空间内声场传播的相干模型[J]. 南京大学学报：自然科学版, 2010， 46(1):26-33.

Research on Optimization of Points Distribution of Noise Measurement in Enclosed Streets

ZHOU Lijun， FANG Tingyong, CHEN Congbo

(School of Civil engineeringschool,Anhui Jianzhu University, Hefei, 230601, China)

Abstract:Enclosed street noise measurement point arrangement optimization problem to improve the efficiency of the noise measuring point has an important impact. Based on the genetic algorithm and using noise analysis software, building an optimized model of a noise measuring points. In the model, the number of measuring points in a large number of noise points is the least and the optimized measurement points are deviated from the original point. Then the optimized model is applied to a specific enclosed street, and the optimal layout of the measuring points is searched out. The results show that the model can reduce the number of noise points and provide a theoretical basis for the noise measurement in the future.

Key words:enclosed street; easuring point, optimization model; enetic algorithm

中图分类号：TU-023

文献标识码：A

文章编号：2095-8382(2016)01-071-05

DOI：10.11921/j.issn.2095-8382.20160115

作者简介：周丽君(1991-)，女，硕士研究生，主要研究方向为绿色建筑及建筑节能。

基金项目：“十二五”国家科技支撑计划课题(2011BAJ03B04)

收稿日期：2015-08-10