基于海浪谱分解与重构的资料同化试验

毛科峰,萧中乐,宋海波,钟奕飞

（1 .解放军理工大学气象海洋学院,江苏南京211101；2 .解放军96631部队,北京102208；3 .解放军92721部队,浙江舟山316000；4 .解放军95857部队,湖南衡阳421000）

数值计算时表达式为:



基于海浪谱分解与重构的资料同化试验

毛科峰1,萧中乐2,宋海波3,钟奕飞4

（1 .解放军理工大学气象海洋学院,江苏南京211101；2 .解放军96631部队,北京102208；3 .解放军92721部队,浙江舟山316000；4 .解放军95857部队,湖南衡阳421000）

摘要:针对有效波高资料提出一种海浪谱分解与重构的资料同化方案:利用历史时段内的有效波高观测资料和模式计算波高场,采用最优插值方法得到分析波高场；在WAV E WAT C H -Ⅲ模式的波浪能量密度谱和有效波高分析值之间引入一个变异系数矩阵,描述模式的误差,以此为状态向量构建卡尔曼滤波系统,对分解过的海浪谱进行修正和重构,得到同化后的海浪谱初始场。利用美国阿拉斯加湾北部海域的7个浮标站进行同化和72 h预报试验,对连续1个月的预报结果进行统计表明:采用该同化方案后24 h预报结果的有效波高均方根误差比未同化的结果降低了0.13 m；同化方案对预报效果的影响可持续36 h左右,随着预报时效延长,同化的效果减弱。

关键词:海浪谱；有效波高；同化；WAV E WAT C H -Ⅲ模式；卡尔曼滤波

1 引言

为了提高海浪模式预测能力,将模式结果和实时资料进行同化,能够改善模式预报的准确度［1］。目前同化的海浪资料包括实测波高和实测海浪谱,由于海浪模式的控制方程是建立在波谱能量平衡方程基础上,观测得到的有效波高对应着波谱能量平衡方程中的波浪能谱的积分,如何用有效波高去同化波浪能谱是资料同化时面临的一个重要问题。Komen［2］首先尝试将实测波高应用于波浪数值模式资料同化的研究,之后Hasselmann等［3］和Bauer等［4］以实测波高与模式计算值之比,作为修正二维波谱的参数去调整海浪谱。这种方法相对简单,但是对波浪谱的调整,比较“粗糙”,没有考虑实测资料对波浪谱方向和频率分布的影响,后来Hasselmann等［5］在波高资料同化研究中改善了波谱修正的尺度因子,也有学者提出将波浪谱分离成风浪和涌浪部分分别同化。另外一方面,在同化高度计波高资料时采用考虑空间效应的修正因子去修正波浪谱,Greenslade和Young［6］采用最优插值方法同化E RS-2高度计资料,研究了观测误差方差和背景误差方差的不同模型和背景误差相关尺度随纬度变化等因素导致的同化效果。E m manouil等［7］发展了一种基于集合卡尔曼滤波方法的波浪资料同化方法,能够结合误差协方差的空间分布特点,使得24 h内,波高的均方根误差减小30 %～60 %。国内的海浪资料同化研究起步较晚,张志旭等［8］通过在台风浪预报中同化高度计资料后改进预报效果。王毅［9］、王毅和余宙文［10］用最优插值方法将卫星高度计的波高资料同化到S WA N模式中,并通过业务预报检验了效果,表明预报效果有一定程度改善。Eeng等［11］采用最优插值方法在S WA N模式中首次同化了台湾岛临近海域的实测资料用于台风浪的预报研究,发现资料同化效果的影响范围取决于台风发展状态及涌浪的传播方向。Guo等［12］利用蒙特卡罗方法模拟计算有效波高的背景误差协方差,并发展了一种新的基于平均波向的有效波高的背景误差协方差模型,用于改进波高资料的同化效果。

目前,利用有效波高资料对波浪模式同化的方法研究是为了将观测波高的信息在物理意义上和空间相关性上去修正模式的波浪能谱。其中风浪和涌浪分离的方案在物理意义上具有优势,然而涌浪的判据和分离本身也是一个较复杂的问题；通过修正尺度因子去调整波浪谱取得了较好的效果,但方法也依赖于经验。因此,本文基于海浪模式中离散的海浪能量密度谱与有效波高的线性关系式,提出一种基于海浪谱分解与重构的波高资料同化方法,并在数值模式中进行预报效果试验分析。

2 有效波高资料的同化方案

2.1 波浪能量密度谱变异系数的引入

海浪模式求解海浪能量密度谱平衡方程时,预报出计算格点上,每个预报时次的波浪能量密度谱E（f,θ）,然后根据波高、周期的统计分布关系式,计算出波浪要素,如平均波高、周期等,其中,有效波高的计算式为:

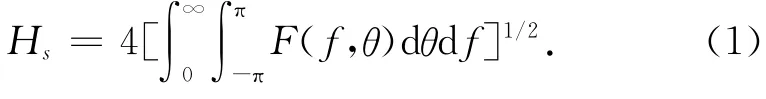
数值计算时表达式为:

式中,Ei,j是频率为fi、方向为θj时离散的波浪能量密度谱值,方向和频率离散的维数是nf和nθ,它表示波浪能量不仅分布在一定的频率范围内,而且分布在相当宽的方向范围内,这描述了海浪内部结构,也能间接地表征海浪外在表现特征。值得注意的是式（1）被离散成式（2）后,与Ei,j构成了一个线性关系式。为了便于区分,本文用表示模式计算的有效波高Hs的真实值,数值模式计算得到的离散波浪能量密度谱值记为,为了描述模式计算的波浪能量密度谱值和真实有效波高之间的误差和关系,引入一个模式计算的波浪能量密度谱和有效波高真值之间的变异系数矩阵,记为Bi,j其维数与相同,则有:

2.2 资料同化的思路

本文的资料同化思路就是基于这个变异系数,描述模式计算的能量密度谱和实测波高之间的误差,以此为状态向量构建卡尔曼滤波系统,对分解过的海浪谱进行修正和重构。为此首先对模式计算得到的较长一段时间内的波浪能量密度谱EMi,j进行经验正交分解,记ek为特征值,对分解出的特征向量进行显著性检验,并判定其物理意义,当式（4）成立时,

ek和ek+ 1是可以分离的,特征值是有意义的。然后将特征值按从大到小的顺序进行排序,这里不妨设下式成立:

选取特征值较大前nk阶特征向量来表示实际的。对t时刻模式得到的波浪能量密度谱Ei,j|t= t简记为Et,它的维数为（nfnθ）,分解成:

ck,t和ek,t是t时刻的k阶的特征向量和特征值,也有:

则式（2）可写为:

式中,Et=（e1,t…ek,t…enk,t）,

因此对于式（3）,可以写成:

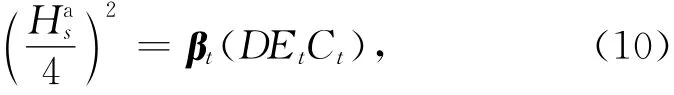
式中,βt是前nk阶特征向量对应的波浪能量密度谱变异系数矩阵,它的维数为（nk×1）。这一线性表达式可以被视为卡尔曼滤波中的量测方程,引入量测噪音εt,它是一维随机向量,则写为:

将波浪能量密度谱变异系数矩阵βt视为卡尔曼滤波系统中的状态向量,用状态方程式（12）描述其变化,和量测方程一起构成卡尔曼滤波系统,

δt- 1是动态噪音,与量测噪音εt一样都是随机向量,假设这两个量满足互不相关,均值为0,方差分别为W 和V ,因此构成如下递推系统:

为了简化表达式,令Xt= DEtCt,则:

利用初始时刻t以前的历史资料通过上述递推系统得到t时刻的变异系数矩阵βt后,就可以利用式（6）重构t时刻的波浪谱,记Ea为同化后的波浪谱,则有:

2.3 有效波高的最优插值方法

式中,Nobs为影响该模式格点的实测浮标站点的数目,Wij则为各观测站点相对于计算格点的最佳权重,下标i表示计算格点,下标j表示浮标观测站。由于实测波高值HO、模式的起始猜测值HP及分析值Ha与真值HT之间有误差存在,要求取各测站对于计算格点的最佳权重,必须求解Nobs组联立方程组,若仅有少量的观测点,则用高斯消元法可求解。故:

若已知真值的条件下,易求得实测值与模式值的均方误差,但实际上,真值未知,故采用已有研究成果中的处理方法［6］,观测误差协方差取为Okj=,其中δkj为kronecher符号,R为实测均方误差与模式均方误差之比。Pkj是观测点k 和j上的模式计算波高的误差协方差,Pik是计算格点i和观测点k的模式计算波高误差协方差。采用Greenslade和Young［6］在海浪同化研究中的方案,波高背景场误差协方差取为:

式中,dkj是观测点k和j之间的距离；σk和σj是观测点k,j上的有效波高背景场的均方根误差；L为影响尺度半径；α、β、γ都是经验常数。

2.4 资料同化的计算步骤

首先选择同化某时刻t之前连续m天的模式计算波高场和方向谱矩阵序列,利用相应时刻的波高观测资料通过最优插值方法得到分析波高场,对方向谱序列进行第一次正交经验分解。选择前nk个主成分,记录前nk个特征向量；然后选取同样时间长度的方向谱样本,用第一次分解得到的nk个空间函数,将之进行第二次正交经验分解,选取同样个数的特征向量。利用第一次分解得到的nk个空间函数和分析波高,进行线性拟合,得到第一组波浪能量密度谱传递系数值；利用第二次正交经验分解得到的nk空间函数和预报点的浪高,进行线性拟合,得到第二组波浪能量密度谱传递系数值。记C0为的误差方差阵,认为是从样本资料直接计算得到,与理论值相等,故C0取为nk阶零方阵。W矩阵主对角线上的值是:Δ/Δt,i = 1,2,3,4 ,其他元素为0,其中,Δ、Δ分别是第一组波浪能量密度谱传递系数值与第二组波浪能量密度谱传递系数对应的差的平方, Δt分母为分解所用数据的时间样本个数。由于量测量只有Hs一个量,故V为1×1矩阵,数值为V = q/（k - m - 1）,q为第一组正交分解后线性回归的残差,预报与实际的差的平方和,k为取得样本个数,即数据的时间个数,m为选取主成分的个数。确定上述参数的取值后,可以利用卡尔曼递推系统得到t时刻的变异系数矩阵βt,然后重构t时刻的波浪谱,得到同化后的初始场。

3 同化预报试验

3.1 资料和海浪模式

为了开展同化预报的数值试验,将波浪计算的区域选为美国阿拉斯加湾北部海域,一个重要的原因是因为该区域能够获得相当数量的波浪实测资料。

（1）同化的浮标资料

浮标资料由美国国家数据浮标中心（N DBC）提供,浮标主要集中在美国阿拉斯加湾北部海域,地理位置如图1示意,浮标的编号和该点的水深情况如表1,采用的是“波浪骑士”浮标,采样频率为1.28 Hz,浮标实测有效波高资料的间隔为1 h。

图1 同化资料的浮标位置Eig .1 The buoys used for assimilation

表1 浮标的位置和水深Tab .1 Buoy coordinates and water depth

（2）WAV E WAT C H -Ⅲ模式

本文的研究基于WAV E WAT C H -Ⅲ第三代海浪数值模式开发了新的资料同化模块,并进行数值试验,模式基于波浪能谱平衡方程:

式中,N即是波作用密度谱,它是频率f、传播方向θ、时间t和地理空间位置的函数,cg为群速,S是能量源汇,关于模式的具体内容见参考文献［13］。

3.2 试验方案

采用不同的初始场方案进行72 h预报设计了两个试验:

（1）试验I:采用模式上次预报的波谱条件初始化后,进行预报72 h；

（2）试验Ⅱ:采用本同化方案得到的初始场进行72 h预报。

海浪模式的计算区域为57.5°～62°N,155°～142.5°W ,如图2。模式的网格分辨率为0.25°× 0.25°,网格总数为51×19；波谱频率范围为0.042～0.413 Hz,离散为25个,波谱方向分辨率为15°,离散为24个方向。模式计算的时间步长为300 s,模式预报结果每间隔1 h输出1次。模式风场驱动采用CCM P风场数据（本文中预报所用的风场都不是实际的预报风场,故在分析预报误差时可忽略风场预报误差导致的海浪预报误差）,CC M P风场的空间分辨率是0.25°×0.25°,每次时间间隔为6 h。水深资料采用美国国家地球物理数据中心（N G D C）提供的E T O P O-1数据。模式物理过程包括深度诱导波破碎、底摩擦耗散作用、白浪耗散作用、非线性4项波相互作用等主要物理过程。这些物理过程的参数化表达式都采用模式的默认设置。

试验过程分为同化得到初始场和进行72 h预报两个过程。以2008年10月21日08时起预报72 h为例说明,图3表示这个同化和预报的过程,预报时间是2008年10月21日08时,同化过程是2008年10月20日08时开始同化至10月21日08时获得同化后的初始场,开始预报,这24 h内同化5个时次的波高观测资料,每个同化时次,利用该时次之前15 d（即m取值为15）的每小时实测资料,对模式计算结果进行有效波高的最优插值,然后根据上述的方案,对格点上有效波高的最优插值波高和模式计算的海浪谱进行波谱分解和重构,之后,数值模式继续同化,具体流程如图3。

3.3 结果分析

（1）初始场对比

用浮标的有效波高实测值对模式计算的波高场（下称背景场）进行最优插值,上式中对L和α、β、γ等经验常数的取值基于前人的研究成果［2］,α= 0,β= 2, γ= 0.5,L = 40 k m,图2中给出了浮标站点的位置和同化浮标资料的计算格点,从图中可见共有51个计算格点的波高经过最优插值订正,形成新的波高分析场,如图4所示。图4a是2008年10月20日08时的模式背景场,图4b是该时刻的分析场,背景场波高偏小的现象,在同化格点上得到了修正。图4c和4d分别为2008年10月20日14时的模式波高背景场和波高分析场,可见到类似的现象,最优插值对波高的影响也由局部范围扩大到整个计算区域。

图2 海浪模式计算区域Eig .2 The waves mode calculation area

图3 同化和预报的流程Eig .3 The flowchart of assimilation and forecast

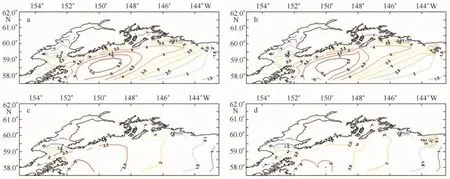
图4 模式计算有效波高场和分析场（m）Eig .4 The significant wave height of model result and analysis fields（m）a .2008年10月20日08时模式背景场,b .2008年10月20日08时分析场,c .2008年10月20日14时模式背景场,d .2008年10月20日14时分析场a .Significant wave height background field at 08:00 of October 20th,2008,b .significant wave height analyticalfield at 08:00 of October 20th, 2008,c .significant wave height background field at 14:00 of October 20th,2008,d .significant wave height analyticalfield at 14:00 of October 20th,2008

得到有效波高的分析场后,构建卡尔曼滤波系统对分解过的波谱进行修正和重构得到模式预报所需的海浪谱初始场。对每个同化计算的格点,用同化时刻之前的15 d的分析场和模式输出的海浪谱,进行波谱修正和重构,得到同化时刻的海浪谱。以2008 年10月21日08时计算格点（57.75°N,144.75°W）为例,图5a是同化之前的海浪方向谱,图5b是同化后的海浪方向谱,该点同化后的方向谱在能量的大小上有一定增大,计算格点（57.75°N,144.50°W）和计算格点（59.50°N,144.50°W）同化后的方向谱在能量的大小和主要频率及谱形状上发生了改变,分别如图6和图7所示。

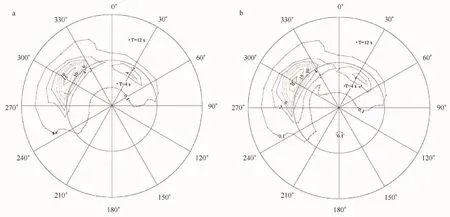
图5 57.75°N,144.75°W格点的方向谱的比较Eig .5 Directional spectra for the grid 57.75°N,144.75°W

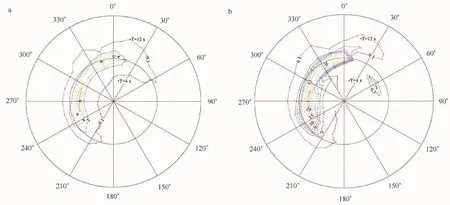
图6 57.75°N,144.50°W格点的方向谱的比较Eig .6 Directional spectra for the grid 57.75°N,144.50°W

（2）预报结果对比分析

试验中m取值为15,即用15 d的方向谱时间序列进行谱分解和重构,取nk为9个主分量。如图8所示,在预报时刻之前进行24 h的资料同化,形成预报时刻的初始场,然后进行预报,以24 h预报结果为例分析同化后的预报效果。图8为连续1个月的浮标站实测有效波高和两个试验方案预报结果的时间序列比较图,时间间隔为1 h。该图和有效波高均方根误差的比较表明未同化的模式预报的有效波高值较实测值普遍偏小,同化后的预报结果与实测值接近,特别是在实测波高较大时同化后效果改进比较明显, 表2给出了这7个测站1个月连续24 h预报效果的统计结果。

图7 59.50°N,144.50°W格点的方向谱的比较Eig .7 Directional spectra for the grid 59.50°N,144.50°W

分别进行了24 h、36 h、48 h、72 h同化预报试验,考察不同预报时效的效果,结果如表2所示。由表2给出的7个测站1个月的预报误差可见,采用同化方法进行预报的结果在24 h内预报效果得到了明显改进。将7个测站的结果平均后,发现同化后有效波高均方根误差较未同化的效果降低了0.13 m；48 h预报效果是同化后有效波高均方根误差较未同化降低了0.05 m；72 h的预报结果中同化后和未同化的有效波高均方根误差没有差别,因此可以认为同化后初始场对预报效果的改善作用已经消失了。

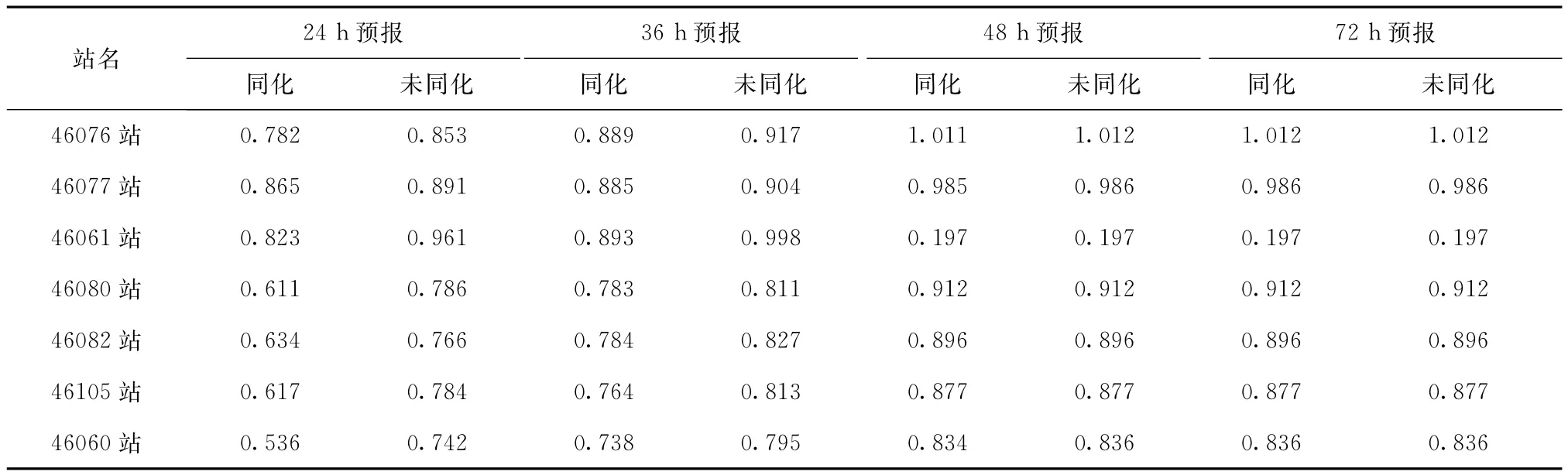
表2 预报结果与浮标观测值的均方根误差统计（单位:m）Tab .2 Statistical parameters R M SE of observed and calculated significant wave height（Unit:m）

通过两个测站同化后和未同化的预报结果的比较来分析同化作用对预报影响的时效。图9a为46077站从10月20日08时至10月21日08时每6 h同化一次后获得10月21日08时的初始场后进行预报的有效波高时间序列,图9b为46105站的结果,在10月21日08时之后的30 h内预报波高和实测符合较好,此后随着时效增长,效果变差,从46077站的结果看,50 h后同化和未同化的结果完全一致。值得注意的是在10月21 日08时之前的24 h内在每间隔6 h的时刻同化了观测资料后,波高会出现“跳跃式变化”,模式计算值会出现突然大于或小于实测波高的现象,波高变化较快。这个现象可能是由于间断的将实测资料与模式进行同化,同化后的波浪谱是在接近实测波高的条件下重构得到的,与模式的平衡关系被打破了,所以模式的计算结果也体现了模式对同化资料后的平衡调整过程。

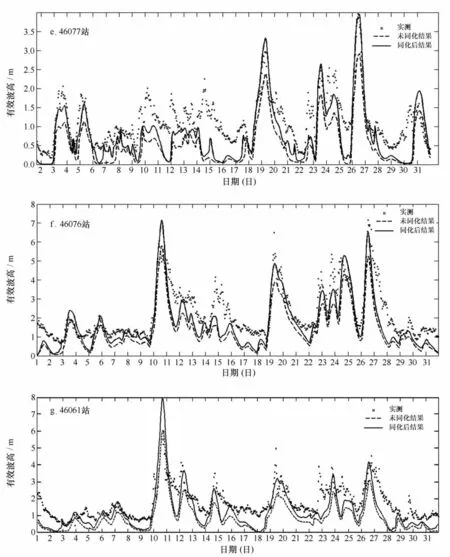
图8 2010年10月有效波高预报结果时间序列比较Eig .8 Time series of observed and calculated significant wave height for the assimilation experiments on October 2010

从整个区域的有效波高等值线也可发现这个现象。图10a为同化后的初始场,图10b为未同化的初始场,图11a和图11b分别为未同化和同化后6 h预报结果,波高的差值分布从同化的格点区域扩散到了整个计算区域。图12a、12b、12c、12d分别为6 h、12 h、36 h、48 h预报结果的差值,从整个区域有效波高预报结果的差值变化图可见,差值从同化的计算格点逐渐扩散到近岸,并减小为0,这也可以认为同化后的初始场对模式的作用是以波浪能量的形式传播影响整个计算区域,因此同化影响的时效和范围也可能与波浪传播的速度有关。

图9 2010年10月有效波高结果和实测比较Eig .9 The time series of observed and calculated significant wave height on October 2010

图10 2010年10月20日08时有效波高（m）预报初始场Eig .10 The initialfields of significant wave height（m）on October 20th,2010

4 小结和讨论

（1）提出一种基于海浪谱分解与重构的海浪有效波高资料同化方案:该方采用最优插值方法得到分析波高场；在模式的波浪能量密度谱和有效波高分析值之间引入一个变异系数矩阵,描述模式的波浪能量密度谱值和有效波高之间的误差关系,以此为状态向量构建卡尔曼滤波系统,对分解过的波谱进行修正,进而重构海浪谱初始场。

（2）通过利用美国阿拉斯加湾的7个浮标站进行同化和预报的数值试验,对连续1个月的24 h预报结果进行统计表明:采用同化方案后预报结果的有效波高均方根误差比未同化的结果降低了0.13 m；同化后初始场对预报效果的影响可持续36 h左右。

图11 6 h有效波高（m）预报结果Eig .11 The significant wave height（m）fields of 6 h forecast

图12 未同化和同化后有效波高预报结果之差（m）Eig .12 Difference of significant wave height for experiments with and without assimilation（m）

（3）文中对最优插值的几个参数的设置主要采用了前人研究成果；对同化方法中波浪方向谱时间序列的天数选取和谱分解的主分量个数设置没有详细讨论,而是直接给出了经验取值,这一点还需进一步研究。

（4）本文的研究只直接同化了有效波高资料,对观测波周期等波浪要素的直接同化也将开展进一步研究,并采用更多源的观测资料来检验同化预报的效果。

参考文献:

［1］ Tolman H L,Banner M L,Kaihatu J M . The N O PP operational wave modelimprovement project［J］. Ocean M odelling,2013,70（5）:2 - 10 .

［2］ Komen G J .Introduction to wave models and assimilation of satellite data in wave models（ocean waves）［M］. Cambridge:Cambridge U niversity Press,1996:554 .

［3］ Hasselmann K,Hasselmann S,Bauer E,et al. Development of a satellite SA R image spectra and altimeter wave height data assimilation system for E RS - 1［R］. Technical Report N ASA - C R - 182685,1988 .

［4］ Bauer E,Hasselmann S,Hasselmann K,et al. Validation and assimilation of Seasat altimeter wave heights using the W A M wave model［J］.Journal of Geophysical Research:Oceans（1978 - 2012）,1992,97（C8）:12671 - 12682 .

［5］ Hasselmann S,Lionello P,Hasselmann K . An optimalinterpolation scheme for the assimilation of spectral wave data［J］.Journal of Geophysical Research:Oceans（1978 - 2012）,1997,102（C7）:15823 - 15836 .

［6］ Greenslade D J M ,Young I R . The impact ofinhomogenous background errors on a global wave data assimilation system［J］.Journal of Atmospheric & Ocean Science,2005,10（2）:61 - 93 .

［7］ E m manouil G,Galanis G,Kallos G . A new methodology for using buoy measurementsin sea wave data assimilation［J］. Ocean Dynamics,2010,60 （5）:1205 - 1218 .

［8］ 张志旭,齐义泉,施平,等.卫星高度计波高资料的同化试验分析［J］.海洋学报,2003,25（5）:21 - 28 . Zhang Zhixu,Qi Yiquan,Shi Ping,et al. Preliminary study on assimilation of significant wave heights from T/P altimeter［J］. Haiyang Xuebao, 2003,25（5）:21 - 28 .

［9］ 王毅.S W A N模式及数据同化技术在海浪预报中的试验研究和应用［D］.青岛:中国海洋大学,2011 . W ang Yi.Study and application of S W A N model and data assimilation technology in wave forecast［D］. Qingdao:China Ocean U niversity,2011 .

［10］ 王毅,余宙文.卫星高度计波高数据同化对西北太平洋海浪数值预报的影响评估［J］.海洋学报,2009,31（6）:1 - 8 . W ang Yi,Yu Zhouwen . Validation ofimpact of assimilation of altimeter satellite significant wave height on wave forecastin the northwest Pacific ［J］. Haiyang Xuebao,2009,31（6）:1 - 8 .

［11］ Eeng X,Zheng J,Yan Y . W ave spectra assimilation in typhoon wave modeling for the East China Sea［J］. Coastal Engineering,2012,69（11）:29 - 41 .

［12］ Guo Y,H ou Y,Zhang C,et al. A background error covariance model of significant wave height employing M onte Carlo simulation［J］. Chinese Journal of Oceanology and Limnology,2012,30（5）:814 - 821 .

［13］ Tolman H L . User manual and system docu mentation of W AV E W AT C HⅢT M version 3.14［S］. Technical Note,M M A B Contribution,2009: 276 .

中图分类号:P731.22

文献标志码:A

文章编号:0253-4193（2016）03-0015-12

收稿日期:2014-12-05；

修订日期:2015-04-02。

基金项目:江苏省自然科学基金（B K20150711）；国家自然科学基金资助项目（11102232）。

作者简介:毛科峰（1981—）,男,湖南省常德市人,讲师,研究方向为海洋环境预报与海洋调查。E-mail:maomaopla @ 163 .com

毛科峰,萧中乐,宋海波,等.基于海浪谱分解与重构的资料同化试验［J］.海洋学报,2016,38（3）:15 - 26,doi:10.3969/j.issn . 0253-4193.2016.03.002

M ao Kefeng,Xiao Zhongle,Song Haibo,et al. Assimilation experiment based on wave spectrum decomposition and reconstruction［J］. Haiyang Xuebao,2016,38（3）:15 - 26,doi:10.3969/j.issn .0253-4193.2016.03.002

Assimilation experiment based on wave spectrum decomposition and reconstruction

M ao Kefeng1,Xiao Zhongle2,Song Haibo3,Zhong Yifei4
（1 .Instituteof Meteorology and Oceanography,PLA University of Science and Technology,Nanjing 211101,China；2 . The 96631 Unitof PLA ,Beijing 102208,China；3 .The 92721 Unitof PLA ,Zhoushan 316000,China；4 . The 95857 Unitof PLA ,Hengyang 102208,China）

Abstract:In the near-shore wave forecasting model,the ocean buoy data assimilation method based on wave spectral decomposition and optimization is proposed . The calculated wave energy spectru m before the initialtime is studied with orthogonal decomposition,and the result,combined with synchronous buoy observations of significant wave height value is used to construct a Kalman filtering system,and the initial wave energy density spectru m of wave modelis revisesd by the multi-time significant wave height value . This method has been applied to 72 h wave forecast experiments with assimilation 7 buoy's significant wave height data in the Gulf of Alaska . One month experiments show that method can improve the forecasts of significant wave height at different degree of different prediction time . The mean square errorfor 24 h forecast of significant wave heightreduces 0.13 m . M eanwhile,the effect ofinitialfield after assimilation to forecast will extend 36 h or so,but the assimilation effectis weakened by extend the prediction time .

Key words:ocean wave spectru m；significant wave height；assimilation；WAV E WAT C H -Ⅲmodel；Kalman filtering