饱和软黏土中不同形状深水防沉板基础承载特性研究

刘润,刘孟孟,杨树耕

（1 .天津大学水利工程仿真与安全国家重点实验室,天津300072）



饱和软黏土中不同形状深水防沉板基础承载特性研究

刘润1,刘孟孟1,杨树耕1

（1 .天津大学水利工程仿真与安全国家重点实验室,天津300072）

摘要:防沉板基础是水下井口、管汇节点与管汇终端等的永久支撑结构,其承受的荷载具有明显的复杂性、非线性和不确定性,给防沉板基础的稳定性研究带来了巨大挑战。本文研究了在剪切强度随深度线性增长的不排水饱和软黏土中,相同用钢量条件下矩形、方形、六边形和圆形防沉板基础的承载特性。采用数值模拟方法确定了竖向荷载V、水平向荷载H（Hx、Hy）、弯矩荷载M（Mx、My）和扭矩荷载T联合作用下,防沉板基础在V - H、V - M、V - T、Hx- Hy、Mx- My、T - H和T - M荷载空间的地基承载力包络线,并建立了相应的拟合公式。研究表明,不同的基础形状对其承载力影响显著,当V较大时,适宜选用圆形基础；当H较为显著时,应选用矩形或方形基础；圆形、方形和矩形基础的抗弯特性分别适用于不同条件下M为主控荷载的情况；当T的影响不可忽视时,矩形或方形基础为首选形式,六边形和圆形基础次之。

关键词:水下生产系统；防沉板基础；基础形状；复合加载；承载力包络线

1 引言

在近海导管架平台的建设中防沉板通常作为临时性的支撑结构用于辅助导管架平台的安装。而在深海油气资源的开发中,钢制的防沉板承担着水下生产系统各个组块（如水下井口、管汇节点、管汇终端等）的荷载并将其递传到地基当中,属于永久性支撑结构,是水下生产系统各组块的基础。由于受到深水施工条件的制约,防沉板作为浅基础具有施工简便、经济性优越的明显优势,是水下生产系统的首选基础形式。工作状态下,防沉板除须承受洋流、波浪、地震等环境荷载作用外,还须承受由其附连结构传递的荷载,如管线热膨胀荷载、跨接管荷载、操作荷载、设备荷载等。由于这些荷载之间存在耦合机制、相互作用复杂、非线性程度高、不确定因素大,使得防沉板基础的稳定性设计面临巨大挑战。

防沉板承载特性的初期研究借鉴了Pramdtl和U ber［1］、Skempton［2］、M eyerhof［3］、Hansen和Christensen［4］、Davis和Booker［5］等对陆上浅基础承载力研究的半经验半理论方法,通过修正系数实现不同条件下防沉板基础的设计,A PI RP 2 A 2000［6］及A PI RP 2 G E O 2011［7］行业设计规范的形成标志着对这些早期研究成果的认可。然而,这些基于陆上浅基础承载特性的研究以确定单一方向极限承载力为目标,与深海防沉板基础同时承受竖向、水平、弯矩和扭矩荷载的复杂作用存在较大差异。自20世纪90年代以来,随着数值模拟技术的不断成熟,承载力包络线法被广泛用于防沉板基础承载特性的研究中。Taiebat和Carter先后于2000年、2002年和2010年研究了圆形防沉板基础在轴心荷载和偏心荷载作用下V - H -M荷载空间的承载力包络线［8 - 10］。Gourvenec等于2006年研究了矩形和方形防沉板基础的竖向承载特性［11］,并于2007年和2008年得到了不同埋深比下两种基础形式的V - H - M空间承载力包络线［12 - 13］。对扭转荷载的研究始于2004年,Einnie和M organ采用极限平衡法得到了圆形、矩形和方形防沉板基础抗扭极限承载力计算公式［14］。2009年,Yun以Einnie的研究成果为基础,采用数值方法分析了3种形式防沉板基础在V - H - T荷载空间内的承载力包络线［15］,但研究中将海床简化为均质土体（剪切强度Su为常数）进行分析。2014年Eeng等［16］较为全面的分析了矩形防沉板基础在三维荷载空间内的承载力包络线,并给出了相应的拟合公式。以上对扭转荷载的研究表明,防沉板的竖向和抗滑移承载特性明显受到扭转荷载的影响。国内这方面的研究较少亦不够深入,仅谭越等［17 - 19］、张晖［20］、高原等［21］结合实际工程给出了运用行业规范对防沉板基础进行设计的示例。

综上所述,防沉板承载力的研究均围绕其不同的形状展开,基础形状决定了防沉板的承载特性。现有的研究成果分别对应于矩形、方形与圆形防沉板基础,对六边形基础的研究少有涉及。本文结合我国的工程实践,研究在相同钢量条件下,不同形状防沉板基础的承载特性,旨在获得不同控制荷载下水下生产系统防沉板基础的最优结构形式,实现防沉板承载效率的最大化。

2 防沉板基础结构形式及数值模型

水下生产系统防沉板基础按其形状可分为矩形基础、方形基础、圆形基础、六边形基础和格栅基础等,这些基础均可根据需要设置裙板和开孔。六边形基础与格栅基础目前仅限于研究当中,矩形、方形和圆形基础在实际工程中均有应用。本文选定矩形、方形、六边形和圆形4种基础形式,以相同钢量为控制指标,对比分析4种基础的承载特性。由于本文研究的4种形式防沉板基础均未设置裙板和开孔且用钢量相同,故4种防沉板基础与土体的接触面积相同,基础高度相等。

参考国外防沉板基础设计实例［16］和国内工程中安装的矩形防沉板基础实例［17—21］确定了防沉板基础尺寸,并采用A B A Q U S建立了4种防沉板基础的三维有限元模型,详细尺寸和模型见表1。模型中荷载作用方向的规定遵从Butterfield等［22］的建议。如图1所示,数值模型中,防沉板基础荷载作用点L RP位于坐标轴原点,即防沉板基础底部与海床土体接触面中心处。实际情况下,深海防沉板基础同时承受竖向、水平、弯矩和扭矩荷载,这些荷载可能存在偏心作用,即荷载作用点并非位于防沉板基础中心。由力学知识可知,这种偏心荷载可由轴心荷载和附加弯矩（或扭矩）荷载组合而成,故本文计算防沉板基础承载特性时,只考虑轴心荷载,实际工程中的偏心荷载承载特性可由V - M、H - T等承载特性获得。

图1防沉板基础示意图及符号说明Eig .1 Sketch and symbols of mudmat foundation

有限元模型中,防沉板基础选用基于理想弹塑性本构模型的高强度钢质材料,弹性模量E = 2.1×1011Pa,泊松比ν= 0.3,密度ρ= 7 850 kg/m3。Randolph［23］深海原位测试结果显示,深海海床土体为软黏土,土体不排水剪切强度Su随深度z线性增加:

式中,k为不排水剪强度线性增长梯度,通常为1～2 kPa/m［24］,Sum为泥面（z = 0）处土体不排水剪切强度。本文土体参数的选取参考了Randolph深海原位测试结果,并假定海床表面水平无倾角。有限元模型中,土体采用基于Tresca屈服准则的理想弹塑性本构模型,土体不排水强度线性增长梯度k = 1.5 kPa/m,泊松比ν= 0.49,Sum= 3.4 kPa,水下有效容重为γ′= 6 k N/m3。

为保证土体破坏时处于小变形状态,防止有限元网格过度畸形,土体剪切模量G取为常量,G/Su= 333,弹性模量E = 2（1 +ν）G。根据以往计算经验,防沉板基础达到水平向极限承载力时基础位移不超过0.01 m；达到抗弯和抗扭极限承载力时基础旋转角度约为4‰。考虑到防沉板基础底部与海床土体之间存在的张力效应,且防沉板基础达到极限承载力时位移和转角较小,此时基础底部尚未与土体分离,故模型中将防沉板基础底面与下部土体完全结合,即接触表面完全粗糙,且防沉板基础与土体接触后不允许分离。数值模型中网格采用局部加密布置,防沉板基础边缘处土体网格尺寸最小为0.05 m,土体边界处网格尺寸最大为5 m。

表1 有限元模型和尺寸Tab .1 FEA model and sizes

计算分两步进行,首先采用位移控制法计算防沉板基础单向加载时的极限承载力,在参考点LRP处直接施加位移荷载,直至土体发生破坏。然后对防沉板基础进行复合加载,综合采用S wipe法和常位移比法求解防沉板基础在各组合荷载空间内的承载力包络线,最终以单向加载模式下的极限承载力为基准将其转化为无量纲二维空间内的地基承载力包络线,采用该方法进行归一化处理的结果具有普适性［25］。

3 单向加载的极限抗力研究

3 .1 单向极限承载力公式

研究单向加载时的极限承载力是评估各种形式防沉板基础承载性能的重要指标,同时也是获得归一化地基承载力包络线的必要过程。目前较为成熟的防沉板承载力计算公式主要针对竖向和水平向承载力。根据A PI RP 2 G E O规范,当基础无埋深、土体的不排水剪强度随深度线性增加时,防沉板的竖向极限承载力公式为:

式中,Vult为竖向极限承载力；E为修正系数,E取值见图2；Suo为基础底部土体不排水剪强度；Nc为无量纲参数,Nc= 5.14；k为土体不排水剪强度随深度线性增长梯度；Kc= 1 + Sc；Sc为形状修正系数；Sc= （0.18 - 0.155κ0.5+ 0.021κ）（1 - 2ic）（B′/L′）；κ= kB/Suo,0≤κ≤25；A′为基础有效面积；B′为基础有效宽度；L′为基础有效长度。

图2 承载力修正系数E取值图Eig .2 Bearing capacity correction factor E

式（2）不仅可以通过等效面积的方法计算其他形状防沉板基础竖向极限承载力,还可通过修正系数E 和kB′/4确定土体不同不排水剪增长梯度k下防沉板基础竖向极限承载力。

该规范中防沉板的水平向极限承载力公式为:

式中,Hult为水平向极限承载力,A为基础面积,Suo为基础底部土体不排水剪强度。

在抗倾覆极限承载力方面,由于其影响因素较为复杂,研究成果较少,故并未形成成熟的抗弯极限承载力计算公式。有代表性的研究成果见于2003年Randolph和Puzrin［26］对条形基础和圆形基础的研究,以及2007年Gourvenec和Randolph对矩形基础研究［11,27］。2014年Eeng等［16］在这些研究的基础上较系统的给出了不同宽长比（B/L）和不同埋深比（d/B）矩形防沉板基础抗弯极限承载力计算公式。其中,x方向抗弯极限承载力:

y方向抗弯极限承载力:

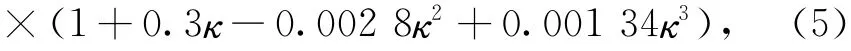
式中,Mx,ult、My,ult分别为x向、y向抗弯极限承载力；B为基础宽度；L为基础长度；d为基础埋深；κ为土体不排水剪强度随深度线性增长梯度。

防沉板抗扭转极限承载力的研究起步较晚,2004 年Einnie和M organ［14］的研究较为系统,采用了极限平衡分析法得到了防沉板的抗扭极限承载力计算公式,其中对于矩形和方形防沉板基础:

圆形防沉板基础:

式中,Tult为抗扭极限承载力；D基础直径；其余符号意义同前。

采用有限元计算方法,得到4种基础单向承载力曲线,进而确定各基础的极限承载力。根据承载力曲线确定极限承载力时,本文采用的原则为:分别计算承载力曲线上各点的曲率半径,其中曲率半径最小点为曲线拐点,其对应的承载力为极限承载力,如图3所示。

图3 防沉板基础竖直向承载力曲线Eig .3 Bearing capacity of mudmat under verticalload

3.2 计算结果对比

分别采用前述的有限元方法和理论公式法计算出4种不同形状防沉板基础在单向加载模式下的地基极限承载力,并进行了比较,结果见表2。

表2 单向加载极限承载力计算结果Tab .2 Uniaxial bearing capacity solutions

由表2可知,数值分析结果与式（2）～（7）的计算结果吻合较好。竖向极限承载力Vult的计算结果表明,相同用钢量条件下圆形基础的极限承载力最高,矩形基础最低,数值计算结果与公式计算结果误差分别为1.3 %和2.0 %。水平极限承载力在x方向Hx,ult的计算结果表明,方形基础的承载性能最优,矩形基础最劣,数值计算结果与公式计算结果误差分别为10.6 %和6.9 %；y方向Hy,ult的计算结果表明,矩形基础承载性能最优,六边形基础最劣,矩形基础数值计算结果与公式计算结果误差达到15.1 %。造成水平向极限承载力误差较大的原因是,当防沉板基础发生水平移动时在防沉板侧面形成土坡（图4）从而产生被动土压力,而式（3）中并未考虑这一因素。因此,水平极限承载力不仅与防沉板基础底面积大小有关,还与基础的几何尺寸和外形有关。

表2中抗弯极限承载力在x方向Mx,ult的计算结果表明,圆形基础承载性能最高,矩形基础最低,其中矩形数值计算结果与公式计算结果误差为2.1 %；y方向My,ult的计算结果显示,矩形基础承载性能最优,六边形基础最劣,其中矩形基础数值计算结果与公式计算结果误差为5.3 %。对比矩形基础Mx,ult和My,ult发现,x和y方向抗弯极限承载力差异较大（接近2倍）,由此可说明矩形防沉板的极限承载力与B/L密切相关。

抗扭计算结果显示,4种基础形式中矩形基础抗扭承载性能最优,圆形基础最劣,数值计算结果与公式（6）～（7）的计算结果误差超过30 % ,造成这一现象的原因是由于不同形状基础的外轮廓角点数目不同,因而防沉板基础扭转时在防沉板侧壁形成的土坡范围和高度也不同,如图5所示。

图4 防沉板基础水平荷载下位移图Eig .4 Displacement of mudmat under horizontalload

由图5可知,防沉板基础承受扭转荷载时,沿扭矩方向防沉板基础侧壁外围土体发生凹陷和隆起（土坡）。矩形基础凹陷和隆起主要发生在基础长边侧,短边侧则不明显；六边形基础在各边侧面均匀的交替出现凹陷和隆起。在相同的扭转荷载作用下,矩形基础土坡隆起高度大于六边形基础,但六边形基础周围土体凹陷和隆起的数目大于矩形基础。

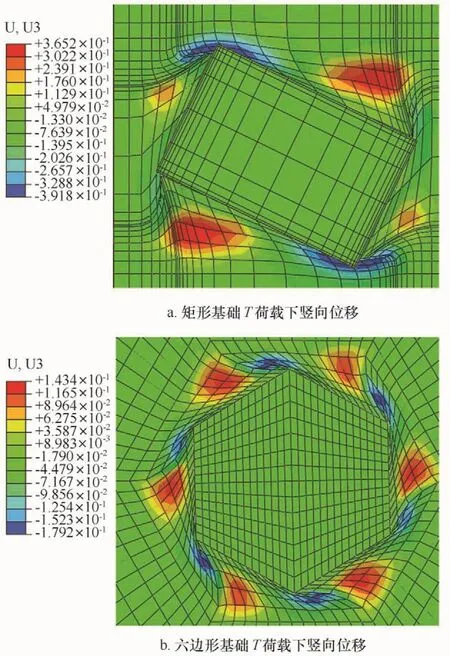
图5 防沉板基础T荷载下竖向位移Eig .5 Displacement of mudmat under torsionalload

4 复合加载模式下地基承载力包络线

作用于防沉板基础上的荷载包括竖向力、水平力、弯矩和扭矩,其中水平力和弯矩存在方向性,本文综合采用Swipe法和常位移比法,对不同荷载组合下防沉板基础的承载力包络线进行研究,并提出相应的计算公式。需要说明的是,本文给出的公式仅适用于确定软黏土中防沉板基础承载特性。

4.1 竖向荷载V作用下的二维荷载空间承载力包络线

4.1.1 V - H荷载空间承载力包络线

通过在有限元模型中施加V - H荷载（M = T = 0）,得到了4种形状防沉板基础在V - H二维荷载空间内的承载力包络线,如图6、图7所示。

由图6、图7可知,4种防沉板基础V - Hx,V -Hy承载力特性差异不大。当竖向荷载V＜750 k N时,V - Hx、V - Hy承载力包络线为水平直线,此时水平荷载Hx、Hy起主要控制作用,包络线大小与防沉板基础Hx,ult、Hy,ult单向极限承载力大小一致,即x向由大至小依次为方形、圆形、六边形和矩形；y向由大至小依次为矩形、方形、圆形和六边形；当竖向荷载V＞750 k N时,V - Hx、V - Hy承载力包络线为多次曲线,此时竖向荷载V起主要控制作用,包络线大小与Vult单向极限承载力大小一致,即由大至小依次为圆形、六边形、方形和矩形。

图6 V - Hx承载力包络线Eig .6 V - Hxfailure envelops

图7 V - Hy承载力包络线Eig .7 V - Hyfailure envelops

为得到具有普适性的结果,采用上文求得的各基础单向极限承载力对防沉板基础包络线进行归一化处理,并与Taibeat和Carter［8］、Gourvenec［12］和Eeng等［16］等的结果进行对比,如图8、图9所示。

由图8、图9可知,采用极限承载力归一化后,4种防沉板基础的V - H承载力包络线仍存在差异,但差异很小。为便于应用,本文给出了4种防沉板基础V - H承载力包络线下限的拟合公式:

式中,h为归一化后水平向荷载,h = Hx/Hx,ult或h =Hy/Hy,ult；v为归一化后竖向荷载,v = V/Vult；θ为水平荷载与x轴夹角,h = Hx/Hx,ult时,θ= 0°；h = Hy/ Hy,ult时,θ= 90°；其余符号意义同前。

图8 归一化V - Hx承载力包络线Eig .8 Normalized V - Hxfailure envelops

图9 归一化V - Hy承载力包络线Eig .9 Normalized V - Hyfailure envelops

4.1.2 V - M荷载空间承载力包络线

通过数值计算得到了4种形状防沉板基础在承受V - M荷载（H = T = 0）时的承载力包络线,如图10、图11所示。

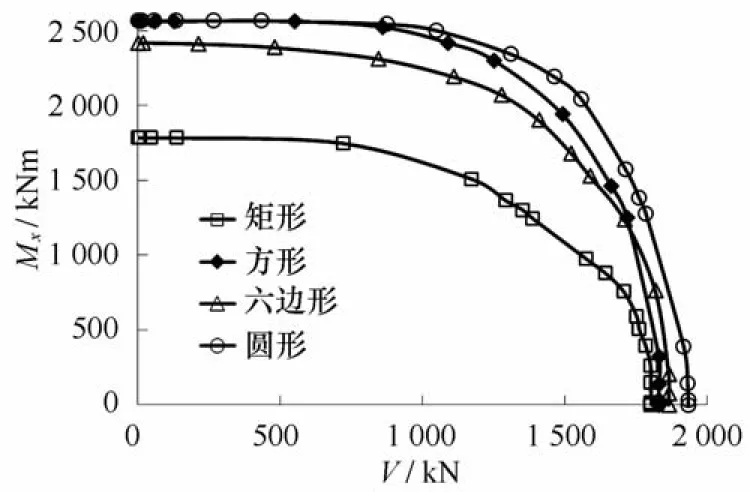
图10 V - Mx承载力包络线Eig .10 V - Mxfailure envelops

由图10、图11可知,4种防沉板基础V - Mx,V - My承载力包络线差异十分明显,这主要是由于4种防沉板基础在抗弯极限承载力方面存在较大的差异。从图中可得到如下结论:（1）在V - Mx荷载空间中,圆形基础承载力包络线在最外围,其次为方形基础、六边形基础,最内侧为矩形基础,其中方形和六边形基础包络线在V≈1 700 k N处相交,但整体上来说,方形基础优于六边形基础；（2）在V - My荷载空间中,矩形基础承载力包络线在最外围,其次为圆形基础、方形基础,最内侧为六边形基础,其中4种基础的包络线在V较大时均有交叉,这是由于各种基础形式抵抗竖向力与弯矩荷载的能力不同所致。

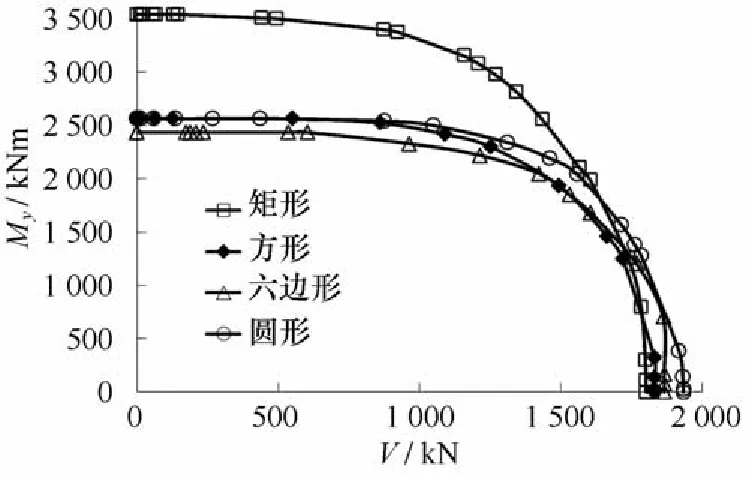
图11 V - My承载力包络线Eig .11 V - Myfailure envelops

由于矩形基础与其他形式基础在V - M空间内的承载力包络线形状差异较大,故需研究该差异对归一化后4种形式防沉板基础承载力包络线的影响,并将归一化结果与Taibeat和Carter［8］、Gourvenec［12］和Eeng等［16］的结果进行对比,如图12、图13所示。

图12 归一化V - Mx承载力包络线Eig .12 Normalized V - Mxfailure envelops

Gourvenec［12］和Eeng［16］采用简单幂曲线（v =（1 - m）p,p与矩形基础宽长比有关）方程拟合了矩形防沉板基础在V - M荷载空间（H = T = 0）内的归一化承载力包络线。但由图12、图13可知,归一化后矩形基础和其他形式基础包络线局部存在差异,对于这种差异,简单幂曲线方程已无法较好的拟合。为解决这一问题,本文采用组合幂曲线方程给出了4种防沉板基础承载力V - M包络线下限的拟合公式:

图13 归一化V - My承载力包络线Eig .13 Normalized V - Myfailure envelops

式中,m为归一化后水平荷载,m = Mx/Mx,ult或m = My/My,ult；γ为弯矩荷载与x轴夹角,m = Mx/Mx,ult,γ = 0°；m = My/My,ult时,γ= 90°；其余符号意义同前。

4.1.3 V - T荷载空间承载力包络线

数值计算发现,防沉板基础在V - T荷载空间（H = M = 0）内的承载力包络线差异较大,且在竖向荷载V约为1 560 k N时存在交点,这是由于各种基础形式抵抗竖向力与扭矩荷载的能力不同所致,如图14所示。

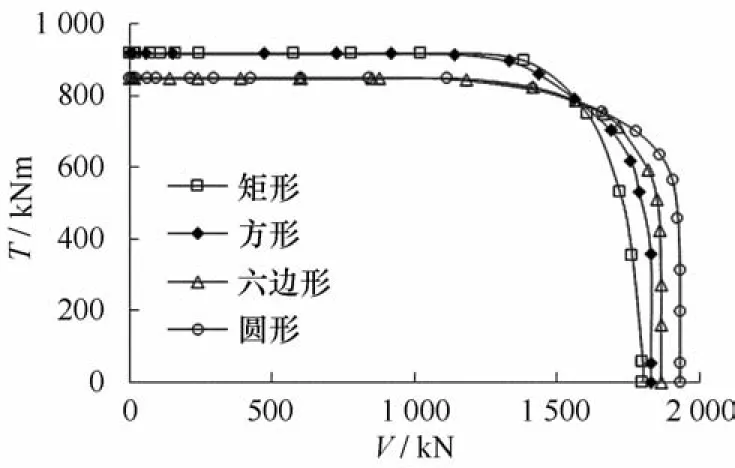
图14 V - T承载力包络线Eig .14 V - T failure envelops

由图14可知,当竖向荷载V小于1 560 k N时,扭矩荷载T对包络线影响较大,此时矩形和方形基础承载性能较高,圆形基础和六边形基础较低；当竖向荷载V大于1 560 k N时,竖向荷载V对包络线影响较大,此时圆形基础最优,六边形基础次之,矩形基础最差。

采用极限承载力归一化处理后4种形状防沉板基础V - T承载力包络线差异很小,2014年Eeng等［16］给出了矩形基础V - T承载力包络线拟合公式:

图15 归一化V - T承载力包络线Eig .15 Normalized V - T failure envelops

式中,t为归一化后水平荷载,t= T/Tult；其余符号意义同前。

由图15可知,Eeng等的结果与数值计算存在一定偏差,为精确的拟合承载力包络线,本文对式（10）中的指数部分进行调整,得到了4种防沉板基础承载力V - T包络线下限的拟合公式:

式中各符号意义同前。

4.2 水平荷载Hres和弯矩荷载Mres的承载力包络线

4.2.1 Hx- Hy荷载空间承载力包络线

实际工程中防沉板基础可能承受沿任意方向的水平荷载Hres,因而需要研究防沉板基础在任意水平荷载Hres作用下（V = M = T = 0）承载力包络线。由于圆形基础为中心对称形式,水平各向承载力均相同,故以下只计算了矩形、方形和六边形基础在Hres为0°、30°、45°、60°、90°时承载特性,并将Hres分解为Hx和Hy两水平方向荷载的组合,得到了Hres作用下承载力包络线,见图16。

2017年6月26日，苏州某地铁线路部分列车在ATO模式下，出现司机界面显示时间不正确，以及在站台停站时间过短的现象。

由图16可知,矩形和方形基础Hx- Hy承载力包络线十分接近,六边形基础则差距较大,说明防沉板基础水平承载力不仅与防沉板和土体接触面积有关,还与滑动时产生的土坡范围和大小密切相关。结合图16和表2中数据来看,这种影响最大能达到10.6 % ,影响较为显著,应当予以重视。

采用极限承载力归一化后3种基础Hx- Hy承载力包络线的差异变小,且形状接近圆形。Eeng等［16］于2014年给出了有埋深矩形防沉板基础在Hx- Hy荷载空间内承载力包络线的拟合公式:

图16 Hx- Hy承载力包络线Eig .16 Hx- Hyfailure envelops

图17 归一化Hx- Hy承载力包络线Eig .17 Normalized Hx- Hyfailure envelops

式中各符号意义同前。

如图17所示,将式（12）结果与有限元结果进行比较可以发现,Eeng等［16］给出的公式可以很好的预测矩形和方形基础承载特性,但高估了六边形基础承载特性。故本文将式（12）中的指数部分进行调整,使其可以满足无埋深六边形基础承载特性。调整后Hx- Hy荷载空间内承载力包络线的拟合公式为:

式中各符号意义同前。

4.2.2 Mx- My荷载空间承载力包络线

防沉板基础承受的真实弯矩Mres可能沿任意方向,同样有必要研究防沉板基础在承受任意弯矩荷载Mres作用下（V = H = T = 0）承载力包络线。以下计算了除圆形外3种基础形式在0°、30°、45°、60°、90°方向Mres作用下承载力包络线,见图18。

图18 Mx- My承载力包络线Eig .18 Mx- Myfailure envelops

图19 归一化Mx- My承载力包络线Eig .19 Normalized Mx- Myfailure envelops

采用极限承载力归一化后三种基础Mx- My承载力包络线的差异明显变小,形状近似于圆形,如图19所示。2014年Eeng等［16］研究了矩形基础在承受任意方向Mres时Mx- My空间内归一化承载力包络线,将其结果整理到图18中,可以看出两者结果十分接近。3种防沉板基础Mx- My承载力包络线下限的拟合公式为:

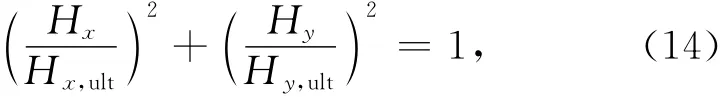
式中各符号意义同前。

4.3 扭矩荷载T作用下的二维荷载空间承载力包络线

4.3.1 T - H荷载空间承载力包络线

由于海底管道沿长度方向存在温差效应,因此管道可能会产生水平屈曲现象。对防沉板基础而言,该现象可导致基础承受由海底管道水平屈曲造成的水平偏心荷载。分析时通常将水平偏心荷载等效为水平轴心荷载H和附加扭转荷载T ,故扭转荷载T对抗滑特性的影响不可忽视。Einnie和M organ［14］、Yun等［15］和Eeng等［16］的研究表明,随着扭转荷载T的增加,地基可承受的水平荷载急速下降。为进一步研究4种形式防沉板基础在承受水平偏心荷载时的承载特性,本文研究了防沉板基础在T - H荷载空间（V = M = 0）内的承载力包络线,见图20、图21。

图20 T - Hx承载力包络线Eig .20 T - Hxfailure envelops

图21 T - Hy承载力包络线Eig .21 T - Hyfailure envelops

由图20、图21可知,当扭转荷载T较小时4种防沉板基础T - Hx,T - Hy承载力包络线差异不大；当扭转荷载T较大时4种基础承载力包络线差异较大,且该差异随着T的增大而增大。总体上,矩形和方形基础优于圆形和六边形基础。

为便于分析,将4种形状防沉板基础T - H承载力包络线进行归一化处理,并将归一化后承载力包络线与Einnie和M organ［14］、Yun等［15］和Eeng等［16］的结果进行对比,如图22、图23所示。

由图22、图23可知,采用极限承载力归一化后的T - Hx,T - Hy承载力包络线差异很小。Einnie和M organ［14］的结果较为保守,Yun等［15］和Eeng等［16］的结果对矩形基础拟合较好,但高估了六边形和圆形基础承载力。由于Einnie和M organ［14］、Yun等［15］和Eeng等［16］的结果均无法精确拟合4种防沉板基础T - H承载力包络线,故本文采用组合幂曲线方程给出了4种防沉板基础承载力T - H包络线下限的拟合公式:

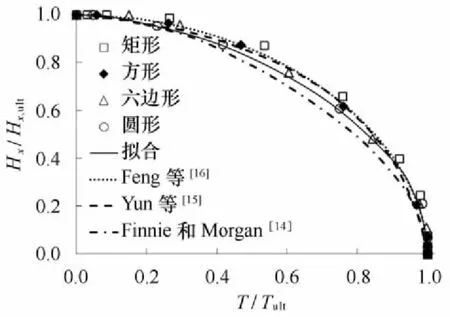
图22 归一化T - Hx承载力包络线Eig .22 Normalized T - Hxfailure envelops

图23 归一化T - Hy承载力包络线Eig .23 Normalized T - Hyfailure envelops

式中,α= 0.45 + cos2θ；β= 0.45 - sin2θ,其余符号意义同前。

4.3.2 T - M荷载空间承载力包络线

Eeng等［16］的研究表明,扭转荷载T对矩形防沉板抗弯特性有显著的影响,但对于其他形状防沉板基础,扭转荷载T对弯矩M的影响尚未明确。为进一步研究4种形式防沉板基础在T - M荷载空间内的承载特性,本文在有限元模型中施加T - Mx、T - My复合荷载（H = V = 0）,得到了4种形式防沉板基础在T - Mx、T - My二维荷载空间内的承载力包络线,见图24、图25。

由图24、图25可知,矩形基础在T - M空间内承载力包络线形状变化剧烈,方形、六边形和圆形基础T - Mx和T - My两方向的承载力包络线基本一致,体现出了较好的稳定性。当有扭转荷载T作用时,Mx方向方形基础承载力最优,圆形基础次之,矩形基础最差；My方向矩形基础承载力最优,方形基础次之,六边形基础最差。

图24 T - Mx承载力包络线Eig .24 T - Mxfailure envelops

图25 T - My承载力包络线Eig .25 T - Myfailure envelops

将4种形状基础在T - M空间内承载力包络线进行归一化处理,并结果与Eeng等［16］的结果进行对比,如图26、图27所示。

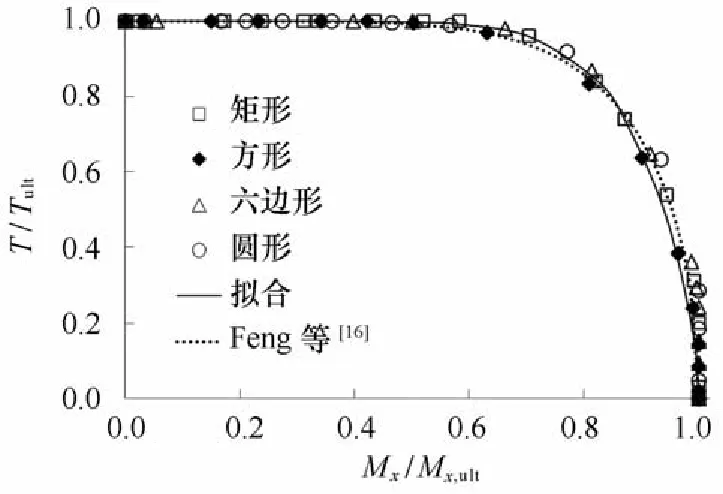
图26 归一化T - Mx承载力包络线Eig .26 Normalized T - Mxfailure envelops

由图26、图27可知,采用极限承载力归一化后4种基础在的T - Mx,T - My承载力包络线差异很小。为便于应用,本文给出了4种防沉板基础T - M承载力包络线下限的拟合公式:

图27 归一化T - My承载力包络线Eig .27 Normalized T - Myfailure envelops

式中各符号意义同前。

5 工程实例验证

以国内某工程实例为例验证上述方法的可靠性,该工程采用矩形防沉板基础。海底土体为淤泥质软黏土,土体不排水强度线性增长梯度k = 1.5 kPa/m,泊松比ν= 0.49,Sum= 3.4 kPa,有效容重为γ′= 6 k N/m3,详细尺寸和荷载参数见表3。

表3 矩形防沉板基础详细参数Tab .3 Detail data for rectangular mudmat

首先按照式（2）～（6）计算防沉板基础单项加载极限承载力和归一化荷载,见表4。

表4 单轴极限承载力和归一化荷载Tab .4 Uniaxial bearing capacity and normalized loads

续表4

得到归一化荷载后按照式（8）～式（16）计算防沉板基础在各荷载空间内的归一化承载力包络线,如图28、图29所示。

图28 V作用下归一化包络线和设计荷载点Eig .28 Normalized failure envelops and design load

由图28、图29可知,归一化后各荷载空间内设计荷载点均位于包络线内部,表明该工程安全。

6 结论

本文主要讨论了矩形、方形、六边形和圆形防沉板基础在用钢量相同的原则下,承受V、H、M、T荷载组合时的承载特性,并给出了4种形状防沉板基础归一化承载力包络线的拟合公式。结论如下:

（1）在单向加载模式下,矩形基础的抗扭承载性能最佳,抗弯性能因其边长的差异而具有独特的优势,就本例而言My,ult/Mx,ult≈2,因而适用于荷载方向明确,且弯矩和扭矩荷载较为突出的情况；方形基础可视为矩形基础的特例（B/L = 1）,各边相等使其各向极限承载力相当；圆形基础竖向承载性能最好,抗扭性能较差,轴对称结构使其各个方向承载性能均衡一致,适用于最大荷载作用方向不突出,扭矩荷载不作为主控荷载的情况；六边形基础在承载性能上无突出优势,其承载能力介于方形基础和圆形基础之间。

（2）在二维复合加载模式下,当V较大时,圆形基础承载力包络线较大,承载性能最优；当H较为显著时,应选用矩形或方形基础；当基础承受的荷载中M起主控作用时,建议根据M的作用方向在圆形、方形和矩形基础中选择较为合适的基础型式；当防沉板基础承受较大的T时,矩形或方形基础为首先型式,六边形和圆形基础次之。

（3）防沉板基础的竖向承载力与基础底面积和基础形状有关；水平向极限承载力与基础底面积、侧边边长和基础形状有关,并受到由于基础水平向变位导致的前方土体变形与抗力的影响；防沉板基础的抗弯极限承载力受到基础形状和宽长比B/L的影响较为显著；抗扭极限承载力受到基础扭转时在侧壁形成的土丘范围和高度的影响,并与基础外轮廓的角点数目相关。

（4）工程设计时可根据设计荷载的特点选用合适的基础形状,然后计算基础的单轴极限承载力,得到归一化后设计荷载,判断该荷载与各荷载空间归一化包络线的位置关系,进而判别设计是否安全。

参考文献:

［1］ Prandt L,U ber P E . Zeitschrift fur Angewandte［J］M athematic and M echanic,1921,1（1）:15 - 20 .

［2］ Skempton A W . The bearing capacity of clays［C］. London:Building Research Congress,1951:180 - 189 .

［3］ M eyerhof G G . The ultimate bearing capacity of foundations［J］. Ge'otechnique,1951,2（2）:301 - 332 .

［4］ Hansen B,Christensen N H . Discussion on theoretical bearing capacity of very shallow footings［J］.Journal of the Soil M ech and Eound,1969,95 （6）:1568 - 1572 .

［5］ Davis E H,Booker J R . The bearing capacity of strip footingsfrom the standpoint of plasticity theory［C］. M elbourne:1st Australia - New Zealand Conference on Geomech,1971:276 - 282 .

［6］ A merican Petraleu m Institute . Recom mended practice for planning,designing and constructing fixed offshore platforms［M］. A merican:A PI Recom mended Practice（RP2 A - W SD）,2000:69 - 71 .

［7］ A merican Petraleu m Institute . Geotechnical and Eoundation Design Considerations［M］. A merican:A NSI/A PI Recom mended Practice 2 G E O, 2011:47 - 66 .

［8］ Taibeat H A,Carter J P . Nu merical studies of the bearing capacity of shallow foundations on cohesive soil subjected to combined loading［J］. Ge' otechnique,2000,50（4）:409 - 418 .

［9］ Taibeat H A,Carter J P . Bearing capacity of strip and circular foundations on undrained clay subjected to eccentric loads［J］. Ge'otechnique,2002, 52（1）:61 - 64 .

［10］ Taibeat H A,Carter J P . A failure surface for circular footings on cohesive soils［J］. Ge'otechnique,2011,61（7）:621 - 622 .

［11］ Gourvene S,Randolph M E,Kingsnorth O . U ndrained Bearing Capacity of Square and Rectangular Eootings［J］.International Journal of Geomechanics,2006,6（3）:147 - 157 .

［12］ Gourvenec S .Shape effects on the capacity of rectangular footings under generalloading［J］. Ge'otechnique,2007,57（8）:637 - 646 .

［13］ Gourvene S . Effect of embedment on the undrained capacity of shallow foundations under generalloading［J］. Ge'otechnique,2008,58（3）:177 -185 .

［14］ Einnie I M S,M organ N . Torsional loading of subsea structure［C］//Proceedings ofthe Eourth International Offshore and Polar Engineering Conference . Toulon,2004:326 - 333 .

［15］ Yun G J,Alasdair M ,John O . U ndrained Capacity of Surface Eootings S

ubjected to Combined V - H - T Loading［C］//Proceedings of the Nineteenth International Offshore and Polar Engineering Conference . Osaka,2009:9 - 14 .

［16］ Eeng X,Randolph M E,Gourvene S,et al. Design approach for rectangular mudmats under fully three-dimensional loading［J］. Ge'otechnique, 2014,64（1）:51 - 63 .

［17］ 谭越,石云,刘明.管道终端及防沉板基础分析［J］.海洋石油,2011,31（3）:93 - 96 . Tan Yue,Shi Yun,Liu Ming .Structure analysis of PLE T and mudmat［J］. Offshore Oil,2011,31（3）:93 - 96 .

［18］ 谭越,刘明,石云.水下管汇结构及防沉板基础分析［C］//第十五届中国海洋工程学术讨论会论文集.山西,2011:485 - 489 . Tan Yue,Liu Ming,Shi Yun .Structure analysis of subsea PLE T and mudmat［C］//Proceedings ofthe Eifteen China Ocean Engineering Academic Conference .Shanxi,2011:485 - 489 .

［19］ 谭越,刘明.水下生产系统防沉板基础分析［J］.船海工程,2011,41（4）:133 - 141 . Tan Yue,Liu Ming . M odel and parameter sensitivity analysis of risers in deepwater［J］.Ship and Ocean Engineering,2011,41（4）:133 - 141 .

［20］ 张晖.水下终端管汇结构设计［J］.中国石油和化工标准与质量,2013,14:63 - 65 . Zhang H ui.Structure design of PLE T［J］. China Petroleu m and Chemical Standard and Quality,2013,14:63 - 65 .

［21］ 高原,桂津,杜永军,等.300米水深PLE T安装技术研究［J］.中国造船,2012,53（2）:65 - 73 . Gao Yuan,Gui Jin,Du Yongjin,et al.Study of PLE T installation in 300 m depth water［J］.Shipbuilding of China,2012,53（2）:65 - 73 .

［22］ Butterfield R,H oulsby G T,Gottardi G .Standardized sign conventions and notation for generally loaded foundations［J］. Géotechnique,1997,47 （5）:1051 -1054 .

［23］ Randolph M E . The Challenges of Deepwater Soft Sediments［R］. Australia:The U niversity of W estern Australia,2012:241 - 271 .

［24］ Randolph M E .Characterization of soft sedimentsfor offshore applications［C］//Proceedings ofthe 2nd International Conference on Site Investigation .2004:209 - 232 .

［25］ 刘润,王磊,丁红岩,等.复合加载模式下不排水饱和软粘土中宽浅式筒型基础地基承载力包络线研究［J］.岩土工程学报,2014,36（1）:146 - 154 . Liu Run,W ang Lei,Ding H ongyan,et al. Eailure envelops oflarge-diameter shallow buried bucket foundation in undrained saturated soft clay under combined loading conditions［J］. Chinese Journal of Geotechnical Engineering,2014,36（1）:146 - 154 .

［26］ Randolph M E,Puzrin A M . U pper bound limit analysis of circular foundations on clay under generalloading［J］. Ge'otechnique,2003,53（9）:785 - 796 .

［27］ Gourvene S . Eailure envelopses for offshore shallow foundations under generalloading［J］. Ge'otechnique,2007,57（9）:715 - 728 .

中图分类号:T U44

文献标志码:A

文章编号:0253-4193（2016）03-0131-14

收稿日期:2015-02-04；

修订日期:2015-08-21。

基金项目:国家重点基础研究发展计划（973计划）（2014CB046802）；国家自然科学基金优秀青年基金（51322904）；天津市自然科学基金面上项目（12JC Y BJC4700）。

作者简介:刘润（1974—）,女,天津市人,博士,教授、博士生导师,主要从事结构物与地基相互作用方面的教学与科研工作。E-mail:liurun @ tju . edu .cn

刘润,刘孟孟,杨树耕.饱和软黏土中不同形状深水防沉板基础承载特性研究［J］.海洋学报,2016,38（3）:131 - 144,doi: 10.3969/j.issn .0253-4193.2016.03.013

Liu Run,Liu M engmeng,Yang Shugeng .Bearing capacity of different shape mudmatfoundations for subsea production system on undrained clays［J］. Haiyang Xuebao,2016,38（3）:131 - 144,doi:10.3969/j.issn .0253-4193.2016.03.013

Bearing capacity of different shape mudmat foundations for subsea production system on undrained clays

Liu Run1,Liu M engmeng1,Yang Shugeng1
（1 .State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China）

Abstract:As the permanent support seabed structures for subsea wells,pipeline manifolds and pipeline terminations,the mudmat foundations have obviously complex,nonlinear and uncertain loading,which makes the research of mudmat foundations' stability a big challenge .In this paper,the bearing capacity of mudmat foundationsin rectangular,square,hexagon and circle are researched under the same steel quantity condition on the deep clay where the strength increases linearly with depth . Nu merical simulation method is utilized to investigate the failure envelops and formulas of mudmat are established in V - H、V - M、V - T、Hx- Hy、Mx- My、T - H & T - M load space,when combined verticalload V ,H orizontalload H ,momentload M ,and torque load T were applied Analysis results show that the shape of mudmat has greatinfluence on its bearing capacity . Concretely,the circular mudmat is suitable on the condition oflarge V load,while the rectangular and square mudmatis better when the H is obvious among allthe loads . W hen M is the controlload,different shapes ofthe mudmat meet different conditions separately . But the rectangular or the square mudmat is optimal and the hexagon or the circle mudmat take second place when the influence of T load cannot be ignored .

Key words:subsea production system；mudmat foundation；shape of foundation；combined load；failure envelop